人教版七年级上册1.2.2数轴 课件(共19张PPT)
文档属性
| 名称 | 人教版七年级上册1.2.2数轴 课件(共19张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-20 09:44:50 | ||
图片预览



文档简介
(共19张PPT)
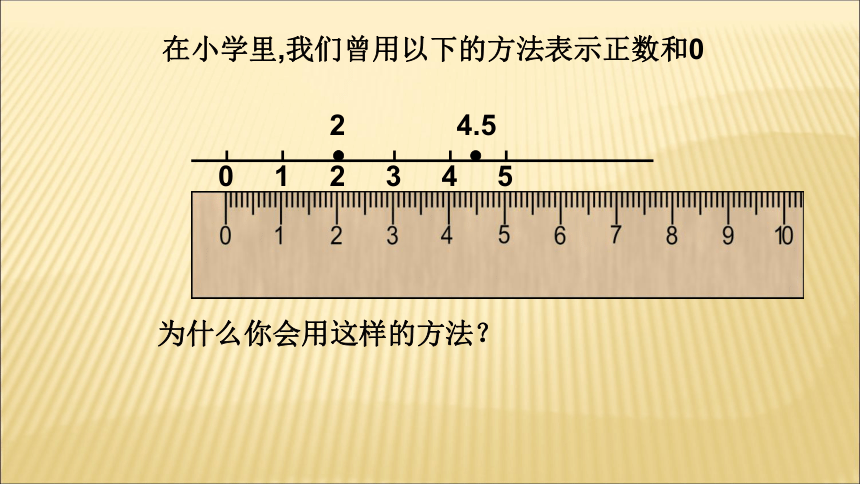
在小学里,我们曾用以下的方法表示正数和0
0 1 2 3 4 5
2
4.5
为什么你会用这样的方法?
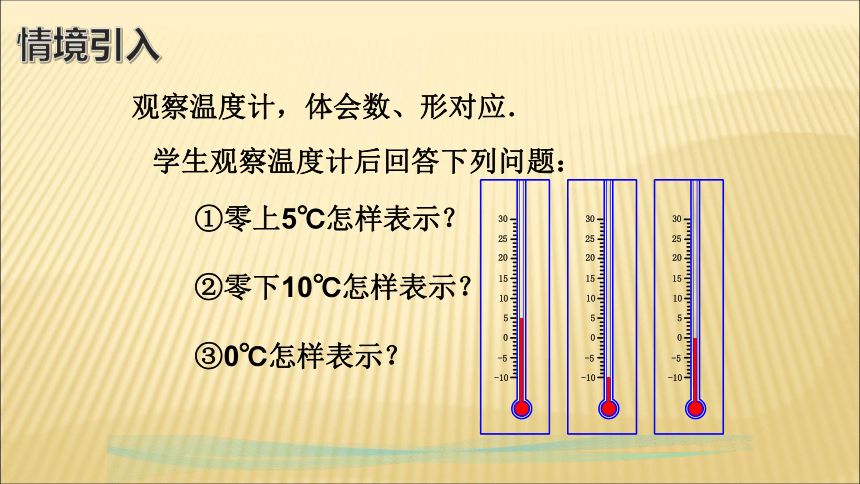
观察温度计,体会数、形对应.
学生观察温度计后回答下列问题:
①零上5℃怎样表示?
②零下10℃怎样表示?
③0℃怎样表示?
学习数轴概念:一般地,在数学中人们用画图把数“直观化”。通常用一条直线上的点表示数,这条直线叫做数轴.
(1)在直线上任取一个点表示数0,这个点叫做原点;
(2)通常规定直线上从原点向右(或上)为正方向,从原点向左(或下)为负方向;
(3)选取适当的长度为单位长度,直线上从原点向右,每隔一个单位长度取一个点,依次表示1,2,3,…;从原点向左,用类似方法表示-1,-2,-3,…
0
正方向
1
2
3
-1
-2
-3
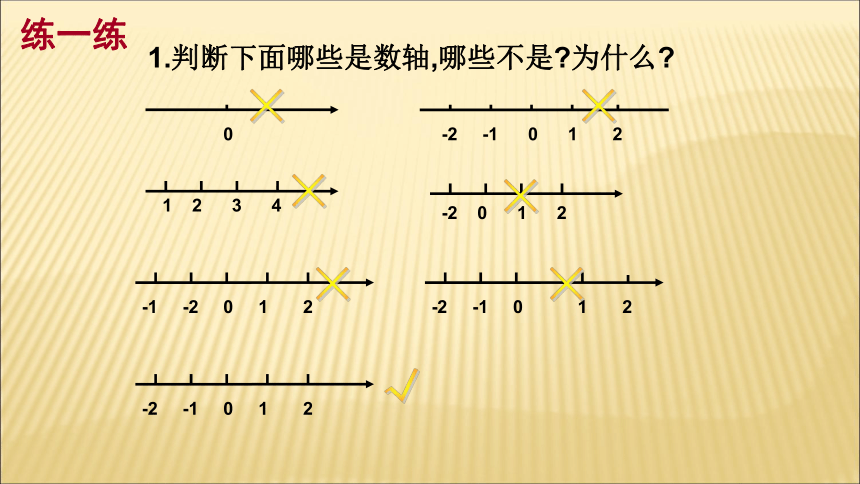
1.判断下面哪些是数轴,哪些不是 为什么
0
-2 -1 0 1 2
1 2 3 4
-2 0 1 2
-1 -2 0 1 2
-2 -1 0 1 2
-2 -1 0 1 2
练一练
A
1
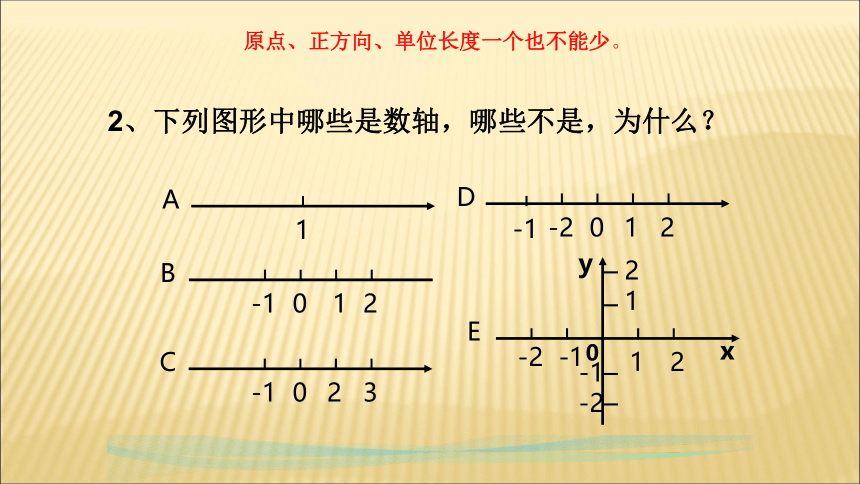
2、下列图形中哪些是数轴,哪些不是,为什么?
B
1
0
2
-1
D
0
-2
1
2
E
1
2
1
2
-1
-1
-2
-2
0
x
y
C
0
-1
2
3
-1
原点、正方向、单位长度一个也不能少。
※思考:你认为数轴最重要的哪三点?
正方向
数轴的三要素
单位长度
原点
画数轴时要注意以下四点:
⒈画直线.
⒉在直线上取一点作为原点.
⒊确定正方向,并用箭头表示.
⒋根据需要选取适当单位长度.
画数轴要体现出数轴的三要素:原点、正方向、长度单位.所有的有理数都可以用数轴的点表示出来.
1、画数轴
0
1
2
3
-1
-2
-3
4
-4
3.5
2、丰富数轴的内涵:分数或小数也可以用数轴上的点来表示,例如从原点向右3.5个单位长度的点表示小数3.5,从原点向左 个单位长度的点表示分数
2
3
-
3、问题:在数轴上能否实际画出表示一千万分之一的点?这个点存在吗?
不能
这个点存在
1、观察数轴上的点的特点:数轴上表示数3的点在原点的右边,与原点的距离是3个单位长度;表示数-2的点在原点的左边,与原点的距离是2个单位长度.
0
1
2
3
-1
-2
-3
4
-4
一般地,设a是一个正数,则数轴上表示数a的点在原点的______边,与原点的距离是______个单位长度;表示数-a的点在原点的______边,与原点的距离是______个单位长度.
右
a
左
a
例1:
(1)画 出数轴并表示下列有理数:
(2)写出数轴上点A、B、C、D、E表示的数:
0
1
2
3
-1
-2
-3
4
-4
1.5
-2
2
-2.5
0
0
1
2
3
-1
-2
-3
4
-4
E
A
B
C
D
点A表示0
点B表示-2
点C表示1
点D表示2.5
点E表示-3
例2:点A在数轴上距原点2个单位长度
(1)当点A位于原点的左侧时,将点A沿数轴正方向移动1个单位长度到点B,则点B表示的数是多少
B
0
1
2
3
-1
-2
A
点B表示的数是-1
例2:(2)在①的基础上,再将点B沿数轴负方向移动3个单位长度到点C,则点C 表示的数是多少
B
0
1
2
3
-1
-2
C
-3
-4
点C表示的数是-4
0
1
2
3
解:
1、画出数轴,并用数轴上的点表示下列各数:
3|2
-5,0,5,-4,
-
3|2
,
4
5
-5
-4
-3
-2
-1
-
3|2
3|2
2、点A在数轴上距原点1个单位长度,点A表示的数是多少?
A
0
1
2
3
-1
-2
A
-3
-4
点A表示的数是1和-1
3、如图,一个点从数轴上的原点开始,先向右移动3个单位长度,再向左移动4个单位长度,可以看出,终点表示的数是-1,已知A、B是数轴上的点,请参照下图,完成填空。
-5 -4 -3 -2 -1 0 1 2 3 4 5
(1)若点A表示-3,把A向右移动7个单位长度,则终点表示的数是 。
(2)若点A表示3,把A向左移动7个单位长度,再向右移动的4个单位长度,则终点表示的数是 。
(3)若把点B向右移动3个单位长度,再向左移动4个单位长度,终点表示的数是0,则点B所表示的数是 。
4、如图,点A与点B的距离是3个单位长度的木条,当木条左端A点落在-9与-8之间,B点落在哪两个整数之间?
-5 -4 -3 -2 -1 0 1 2 3 4 5
5、如图,以P点为圆心,3个单位长度为半径画圆,该圆与数轴交点表示的数是多少?
-5 -4 -3 -2 -1 0 1 2 3 4 5
P
1、小强写作业时不慎将墨水滴在已画好的数轴上.试根据图中数据,确定被墨迹遮盖住的整数共有几个?并写出分别是哪些整数?
2、数轴上,与原点距离5个单位长度的点表示的数是
(1)数轴概念:一般地,在数学中人们用画图把数“直观化”.通常用一条直线上的点表示数,这条直线叫做数轴.
(2)数轴的三要素:原点、正方向、长度单位
(3)数与形的关系:一 一对应的关系.
(4)数学思想:数形结合的思想.
在小学里,我们曾用以下的方法表示正数和0
0 1 2 3 4 5
2
4.5
为什么你会用这样的方法?
观察温度计,体会数、形对应.
学生观察温度计后回答下列问题:
①零上5℃怎样表示?
②零下10℃怎样表示?
③0℃怎样表示?
学习数轴概念:一般地,在数学中人们用画图把数“直观化”。通常用一条直线上的点表示数,这条直线叫做数轴.
(1)在直线上任取一个点表示数0,这个点叫做原点;
(2)通常规定直线上从原点向右(或上)为正方向,从原点向左(或下)为负方向;
(3)选取适当的长度为单位长度,直线上从原点向右,每隔一个单位长度取一个点,依次表示1,2,3,…;从原点向左,用类似方法表示-1,-2,-3,…
0
正方向
1
2
3
-1
-2
-3
1.判断下面哪些是数轴,哪些不是 为什么
0
-2 -1 0 1 2
1 2 3 4
-2 0 1 2
-1 -2 0 1 2
-2 -1 0 1 2
-2 -1 0 1 2
练一练
A
1
2、下列图形中哪些是数轴,哪些不是,为什么?
B
1
0
2
-1
D
0
-2
1
2
E
1
2
1
2
-1
-1
-2
-2
0
x
y
C
0
-1
2
3
-1
原点、正方向、单位长度一个也不能少。
※思考:你认为数轴最重要的哪三点?
正方向
数轴的三要素
单位长度
原点
画数轴时要注意以下四点:
⒈画直线.
⒉在直线上取一点作为原点.
⒊确定正方向,并用箭头表示.
⒋根据需要选取适当单位长度.
画数轴要体现出数轴的三要素:原点、正方向、长度单位.所有的有理数都可以用数轴的点表示出来.
1、画数轴
0
1
2
3
-1
-2
-3
4
-4
3.5
2、丰富数轴的内涵:分数或小数也可以用数轴上的点来表示,例如从原点向右3.5个单位长度的点表示小数3.5,从原点向左 个单位长度的点表示分数
2
3
-
3、问题:在数轴上能否实际画出表示一千万分之一的点?这个点存在吗?
不能
这个点存在
1、观察数轴上的点的特点:数轴上表示数3的点在原点的右边,与原点的距离是3个单位长度;表示数-2的点在原点的左边,与原点的距离是2个单位长度.
0
1
2
3
-1
-2
-3
4
-4
一般地,设a是一个正数,则数轴上表示数a的点在原点的______边,与原点的距离是______个单位长度;表示数-a的点在原点的______边,与原点的距离是______个单位长度.
右
a
左
a
例1:
(1)画 出数轴并表示下列有理数:
(2)写出数轴上点A、B、C、D、E表示的数:
0
1
2
3
-1
-2
-3
4
-4
1.5
-2
2
-2.5
0
0
1
2
3
-1
-2
-3
4
-4
E
A
B
C
D
点A表示0
点B表示-2
点C表示1
点D表示2.5
点E表示-3
例2:点A在数轴上距原点2个单位长度
(1)当点A位于原点的左侧时,将点A沿数轴正方向移动1个单位长度到点B,则点B表示的数是多少
B
0
1
2
3
-1
-2
A
点B表示的数是-1
例2:(2)在①的基础上,再将点B沿数轴负方向移动3个单位长度到点C,则点C 表示的数是多少
B
0
1
2
3
-1
-2
C
-3
-4
点C表示的数是-4
0
1
2
3
解:
1、画出数轴,并用数轴上的点表示下列各数:
3|2
-5,0,5,-4,
-
3|2
,
4
5
-5
-4
-3
-2
-1
-
3|2
3|2
2、点A在数轴上距原点1个单位长度,点A表示的数是多少?
A
0
1
2
3
-1
-2
A
-3
-4
点A表示的数是1和-1
3、如图,一个点从数轴上的原点开始,先向右移动3个单位长度,再向左移动4个单位长度,可以看出,终点表示的数是-1,已知A、B是数轴上的点,请参照下图,完成填空。
-5 -4 -3 -2 -1 0 1 2 3 4 5
(1)若点A表示-3,把A向右移动7个单位长度,则终点表示的数是 。
(2)若点A表示3,把A向左移动7个单位长度,再向右移动的4个单位长度,则终点表示的数是 。
(3)若把点B向右移动3个单位长度,再向左移动4个单位长度,终点表示的数是0,则点B所表示的数是 。
4、如图,点A与点B的距离是3个单位长度的木条,当木条左端A点落在-9与-8之间,B点落在哪两个整数之间?
-5 -4 -3 -2 -1 0 1 2 3 4 5
5、如图,以P点为圆心,3个单位长度为半径画圆,该圆与数轴交点表示的数是多少?
-5 -4 -3 -2 -1 0 1 2 3 4 5
P
1、小强写作业时不慎将墨水滴在已画好的数轴上.试根据图中数据,确定被墨迹遮盖住的整数共有几个?并写出分别是哪些整数?
2、数轴上,与原点距离5个单位长度的点表示的数是
(1)数轴概念:一般地,在数学中人们用画图把数“直观化”.通常用一条直线上的点表示数,这条直线叫做数轴.
(2)数轴的三要素:原点、正方向、长度单位
(3)数与形的关系:一 一对应的关系.
(4)数学思想:数形结合的思想.
