12.1平方差公式 课件

课件16张PPT。§12.1平方差公式 曹县磐石回中 蔡艳平
（1） (a+5)(a-5) （2）(a+3)(a-3）
（3）（5-a)(5+a) (4) (3-a)(3+a)
3、观察第2题几个乘式中的因式以及它们的乘积，
你能快速写出 下列各题的运算结果吗？
（m-7)(m+7)= , ,
（m+n)(m-n)= .
2、回忆多项式与多项式相乘法则,计算下列各题温故知新： （1）(7ab)2 = （2） (-3a)2 =1、回忆积的乘方与幂的乘方法则。49a2b29a2 （3）(a3)2 = （4） (-6ab2)2 = 36a2b4a6a2-9a2-25
25-a2 9-a2重点：掌握并运用平方差公式。
难点：灵活运用平方差公式解决问题。1.会推导平方差公式,能说出公式的结构特征,能运用平方差公式进行乘法运算。
2.经历探索平方差公式的过程,了解公式的几何背景,进一步体会公式的实际意义。
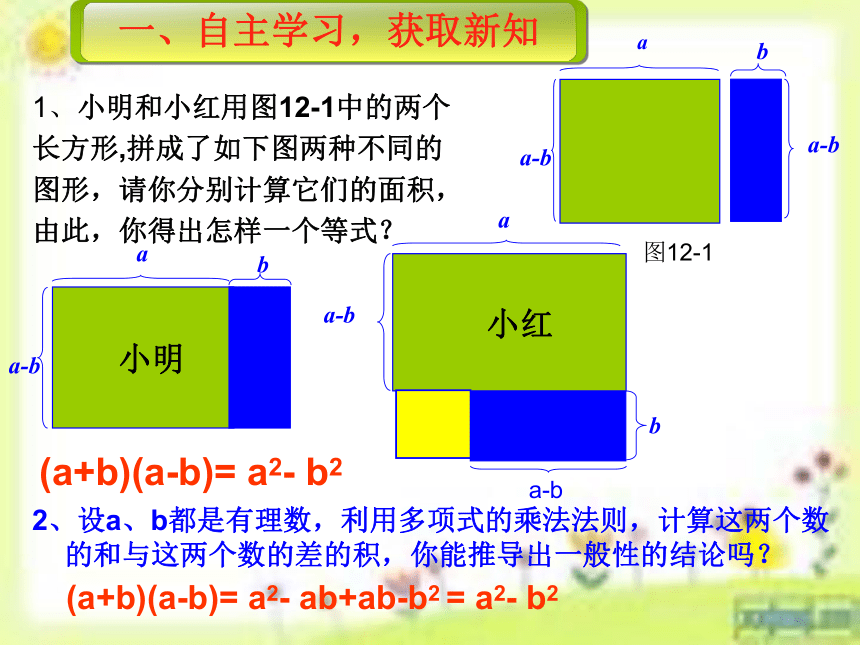
3.发展符号意识，体会“特殊 —— 一般 —— 特殊”的认识规律。1、小明和小红用图12-1中的两个
长方形,拼成了如下图两种不同的
图形，请你分别计算它们的面积，
由此，你得出怎样一个等式？(a+b)(a-b)= a2- b22、设a、b都是有理数，利用多项式的乘法法则，计算这两个数的和与这两个数的差的积，你能推导出一般性的结论吗？
(a+b)(a-b)= a2- ab+ab-b2 = a2- b2
3、平方差公式
(a + b)(a - b)= a2- b2
你能说出平方差公式有哪些结构特征吗？两个数的和与这两个数的差的乘积，
等于这两个数的平方差.
结构
特征
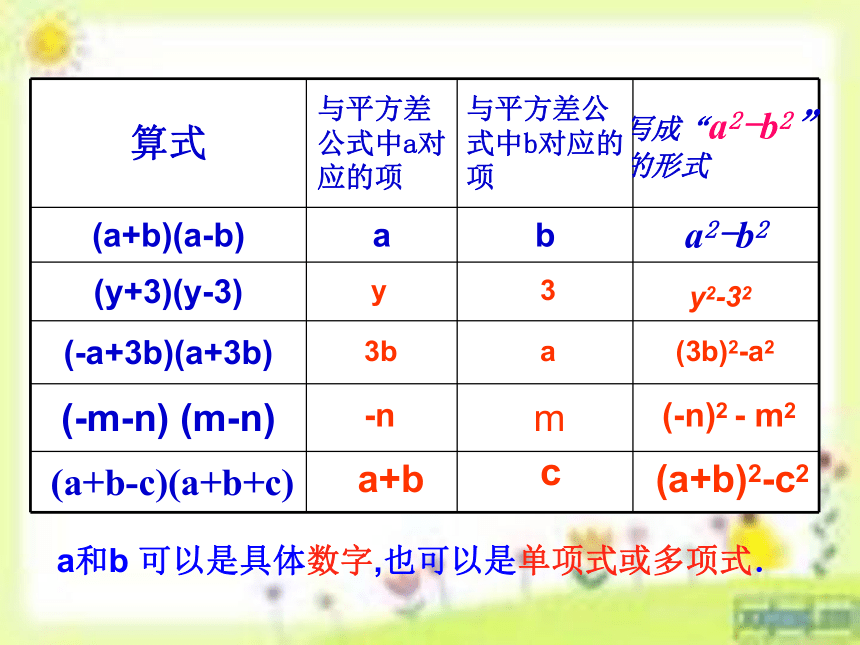
4、平方差公式(a+b)(a-b)= a2-b2的结构特征(1) 左边两个二项式相乘，这两 个二项式有一项完全相同，另一项互为相反数。(2) 公式右边是乘数中两个数的平方差（相同项的平方减去相反项的平方）； ｛（3）公式中的字母可以是具体的数字，也可以是多项式或单项式。 a和b 可以是具体数字,也可以是单项式或多项式．
y3y2-323ba(3b)2-a2m(-n)2 - m2a+b(a+b)2-c2-nc三、课堂体验，成果展示2、运用平方差公式计算下列各题：1. (3x+2) (3x-2)2. (b+2a) (2a-b)3. (-x+2y) (-x-2y)4. (m3-n) (m3+n)=(3x)2-4
=9x2-4=(2a)2-b2
=4a2-b2=(-x)2-(2y)2
=x2-4y2=(m3)2-n2
=m6-n2 2、 这是我们的磐石回中的操场,它的长为103米, 宽为97米.你能用平方差公式计算出它的面积吗？(1+2x)(1?2x)
=1?2x2
(2) (b2+2a)(?b2+2a)
= ? b4+2ab2 ?2ab2+4a2
=4a2 ? b4
(3) (? 3m+2n)(3m?2n)
= 9m2-4n21、下列计算是否正确？方法是否得当？第二数在平方时未加括号没有灵活运用
平方差公式误用
平方差公式四、当堂反馈，查缺补漏2、请运用平方差公式计算下列各题：
（1）19×21
（3)(2x-5)(2x+5)-（7+2x)(2x-7)=(2x)2-52-[(2x)2-72]
=4x2-25-[4x2-49]
=4x2-25-4x2+49
=24
（2）(x+y)(x-y)(x2+y2) =(x2-y2)(x2+y2)
=x4-y4
=(20-1) ×(20+1)
=202-12
=400-1
=399
通过本节课的学习你有哪些收获？课堂小结平方差公式 (a+b)(a?b)=a2?b2。运用平方差公式时，要紧扣公式的特征，
找出相等的“项”和符号相反的“项”，
然后应用公式.
一、填空：
1. (2x+3y)(2x-3y)=_____ ; (x+2) ( ) =x2-4
(x-3)(x+3)(x2+9)=_____ ; (2x+1)(2x-1) +1=_____
二、选择题
3.下列多项式乘法中不能用平方差公式计算的是（ ）
A.(a3-b3)(a3+b3) B.(a2+b2)(b2-a2)
C.(2xy+1)(2xy-1) D.(x2y-5)(y2x+5)
三、计算
4.（b+a）(b-a) + (b+c) (-b+c)
达标检测4x2-9y2X-2X4-814x2D-a2+c2 选做题：计算
(1) (-3x2+5)(-3x2-5)-x2(3x+4)(3x-4)-16 (-x)2
-25316-216作业
必做题 P112 1 、2
选做题 P112 5谢谢大家,再见！