11.1平面内点的坐标(3) 课件(共28张PPT)
文档属性
| 名称 | 11.1平面内点的坐标(3) 课件(共28张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 972.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-22 00:00:00 | ||
图片预览








文档简介
(共28张PPT)
沪科版 八年级上册
11.1 平面内点的坐标(3)
教学目标
1.灵活建立平面直角坐标系确定点的位置.
2.已知点的坐标能够知道点所在象限或坐标轴.
3.掌握点在平面直角坐标系中一些简单规律.
教学重点:
理解平面直角坐标系各象限内点的距离特征,并会由这些特征确定点所在平面直角坐标系的象限;
理解平面直角坐标系各象限内点的符号特征,并会由符号特征确定点所在平面直角坐标系象限.
教学难点:
知道平面直角坐标系各象限内点的特征,并会由这些距离特征确定点所在平面直角坐标系的象限.
x轴上的点的纵坐标为0,表示为(x,0)
y轴上的点的横坐标为0,表示为(0,y)
第一象限:(+,+) 第二象限:(-, +)
第三象限:(-,-) 第四象限:(+, -)
平面直角坐标系内点的坐标的特征
复习旧知
2.若点(a+5,a-3)在y轴上,则a的值
为 ,该点的坐标为 .
1.若点(a+5,a-3)在x轴上,则a的值
为 ,该点的坐标为 .
3
-5
(0,-8)
(8,0)
温故新知
3.在同一坐标系中,如果(3a+1,b-2)与(-5,1)所示的位置相同,则a= ,b= .
-2
3
4.已知(a-2)2 +︱b+3 ︱=0,则P(-a,-b)的坐标为 .
(-2,3)
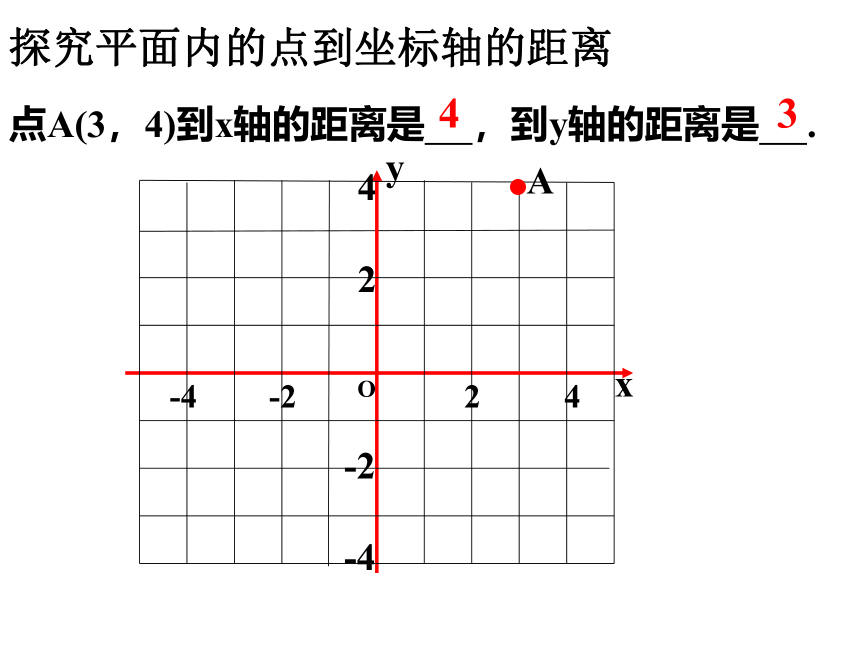
点A(3,4)到x轴的距离是 ,到y轴的距离是 .
4
3
x
y
-4 -2 2 4
O
4
2
-2
-4
A
探究平面内的点到坐标轴的距离
1.点A(2,5)到x轴的距离是 ,到y轴的距离是 ;
2.点B(-2,5)到x轴的距离是 ,到y轴的距离是 ;
3.点C(2, -5)到x轴的距离是 ,到y轴的距离是 ;
4.点D (-2,-5)到x轴的距离是 ,到y轴的距离是 .
5
2
5
2
5
2
5
2
探究平面内的点到坐标轴的距离
1.点A(2,5)到x轴的距离是 ,到y轴的距离是 ;
2.点B(-2,5)到x轴的距离是 ,到y轴的距离是 ;
3.点C(2, -5)到x轴的距离是 ,到y轴的距离是 ;
4.点D (-2,-5)到x轴的距离是 ,到y轴的距离是 .
5
2
5
2
5
2
5
2
点P(a,b)到x轴的距离是 ,到y轴的距离是 .
︱b︱
︱a︱
探究平面内的点到坐标轴的距离
已知x轴上的P到y轴的距离为3,则点P的
坐标为__________________
(3,0)
或(-3,0)
例2 如图,正方形ABCD的边长为4,请建立一个平面直角坐标系,并写出正方形的四个顶点A,B,C,D在这个平面直角坐标系中的坐标.
A
B
C
D
建立平面直角坐标系表示图形的坐标
例2 如图,正方形ABCD的边长为4,请建立一个平面直角坐标系,并写出正方形的四个顶点A,B,C,D在这个平面直角坐标系中的坐标.
解:如图,以顶点A为原点,AB所在直线为x轴,AD所在直线为y轴建立平面直角坐标系.
A
B
C
D
此时,正方形的四个顶点A,B,C,D的坐标分别为:
x
y
A(0,0), B(4,0),
C(4,4),D(0,4).
O
例2,如图11-8,正方形ABCD的边长为4,请建立一个平面直角坐标系,并写出正方形的四个顶点A,B,C,D在这个平面直角坐标系中的坐标。
解:如图,以顶点C为原点,DC所在直线为x轴,BC所在直线为y轴建立平面直角坐标系。
A
B
C
D
此时,正方形的四个顶点A,B,C,D的坐标分别为:
x
y
A(-4,-4), B(0,-4),
C(0,0),D(-4,0).
O
A
B
C
D
x
y
O
由上得知,建立的平面直角坐标系不同,则各点的坐标也不同.你认为怎样建立直角坐标系才比较适当?
平面直角坐标系建立得适当,可以容易确定图形上的点,例如以正方形的两条边所在的直线为坐标轴,建立平面直角坐标系.又如可按图建立平面直角坐标系.
A
B
C
D
x
y
O
建立的平面直角坐标时,要记得标注x轴、y轴和坐标原点O.建立的平面直角坐标系不同,则各点的坐标也不同.
建立不同的平面直角坐标系,同一个点就会有不同的坐标,但正方形的形状和性质不会改变.
例.如图,已知△ABC在方格中,顶点A的坐标为(0,3).请在图中建立适当的平面直角坐标系,并根据所建立的平面直角坐标系写B,C的坐标.
A
B
C
解:
∵ 点A的横坐标为0,
∴ 点A在y轴上,
∵ 点A的纵坐标为3,
∴ 坐标原点在点A的正
下方且与点A的距离为3.
典型例析
A
B
C
解:
∵ 点A的横坐标为0,
∴ 点A在y轴上,
∵ 点A的纵坐标为3,
∴ 坐标原点在点A的正
下方且与点A的距离为3.
∴ 取过坐标原点的水平数轴为轴,向右为 正方
向,取过坐标原点的竖直数轴为y轴,向上为
正方向,建立平面直角坐标系,如图所示.
x
O
∴ 点B的坐标是(-3,-1),
点C的坐标是(1,1).
y
1.如图,建立适当的平面直角坐标系后,点B,C在这个平面直角坐标系中的坐标分别为(0,1),
(1,-1),则点A的坐标为( ).
A
B
C
练习巩固
A.(-1,2)
B.(2,-1)
C.(-2,1)
D.(1,-2)
A
2. 如图,在正方形ABCD中,已知点A,B,C的坐标分别是(1,1), (-1,1), (-1,-1), 则点D的坐标是 ( ).
A
B
C
D
A.(-1,0)
B.(1,0)
C.(1,-1)
D.(0,-2)
C
3. 已知点A(-4,3)和点B(-8,3),则点A,B之间的距离是 ( ).
A.3 B.4 C.8 D.12
B
4. 若点A(2,-4)和点B(a,-4)之间的距离是3,则a的值为 ( ).
A.3 B.5 C. -1 D.5或-1
D
5. 过点A(-1,-1)和点B(-1,5)作直线AB,则点AB ( ).
A.与y轴平行 B.与x轴平行 C.与y轴相交 D.无法确定
A
6. 已知点A的坐标为 (n+3,3),点B的坐标为(n-4,n),AB∥x轴,则AB的长为 ( ).
A.5 B.6 C. 7 D.13
C
7.如图,在5×4的方格纸中,每个小正方形边 长
为1,点O,A,B在方格纸的交点(格点)上,在
第四象限内的格点上找点C,使△ABC的面积
为3,则这样的点C共有( ).
A.2个 B.3个
C.4个 D.5个
A
B
x
y
B
图书馆
教学楼
旗杆
校门
实验楼
8.某学校的平面示意图如图所示,如果实验楼所在位置的坐标为(-2,-3) ,教学楼所在位置的坐标为(-1,2) ,请你建立坐标系,并写出图书馆,校门,旗杆的坐标.
x
y
O
图书馆,校门,旗杆的坐标分别是:
(-4,3), (-4,0),
(0,0).
解:
9.现有一张利用平面直角坐标系画出来的某
公园景区地图,如图所示,若知道游乐园D的坐标
为(2,-2).
(1)请按题意建立平面直角坐标系;
(2)写出其他景点的坐标;
(3)请指出哪个景点距离原点最近?
哪个景点距离原点最远?
(3)望春亭距离原点最近;牡丹园距离原点最远.
x
y
O
(-2,-1)
(-3,2)
(0,4)
(3,3)
雁塔
中心广场
钟楼
大成殿
科技大学
碑林
影月湖
如图,是某城市旅游景点的示意图.你是如何确定各个景点的位置的?
今天作业
课本P9页第4题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
沪科版 八年级上册
11.1 平面内点的坐标(3)
教学目标
1.灵活建立平面直角坐标系确定点的位置.
2.已知点的坐标能够知道点所在象限或坐标轴.
3.掌握点在平面直角坐标系中一些简单规律.
教学重点:
理解平面直角坐标系各象限内点的距离特征,并会由这些特征确定点所在平面直角坐标系的象限;
理解平面直角坐标系各象限内点的符号特征,并会由符号特征确定点所在平面直角坐标系象限.
教学难点:
知道平面直角坐标系各象限内点的特征,并会由这些距离特征确定点所在平面直角坐标系的象限.
x轴上的点的纵坐标为0,表示为(x,0)
y轴上的点的横坐标为0,表示为(0,y)
第一象限:(+,+) 第二象限:(-, +)
第三象限:(-,-) 第四象限:(+, -)
平面直角坐标系内点的坐标的特征
复习旧知
2.若点(a+5,a-3)在y轴上,则a的值
为 ,该点的坐标为 .
1.若点(a+5,a-3)在x轴上,则a的值
为 ,该点的坐标为 .
3
-5
(0,-8)
(8,0)
温故新知
3.在同一坐标系中,如果(3a+1,b-2)与(-5,1)所示的位置相同,则a= ,b= .
-2
3
4.已知(a-2)2 +︱b+3 ︱=0,则P(-a,-b)的坐标为 .
(-2,3)
点A(3,4)到x轴的距离是 ,到y轴的距离是 .
4
3
x
y
-4 -2 2 4
O
4
2
-2
-4
A
探究平面内的点到坐标轴的距离
1.点A(2,5)到x轴的距离是 ,到y轴的距离是 ;
2.点B(-2,5)到x轴的距离是 ,到y轴的距离是 ;
3.点C(2, -5)到x轴的距离是 ,到y轴的距离是 ;
4.点D (-2,-5)到x轴的距离是 ,到y轴的距离是 .
5
2
5
2
5
2
5
2
探究平面内的点到坐标轴的距离
1.点A(2,5)到x轴的距离是 ,到y轴的距离是 ;
2.点B(-2,5)到x轴的距离是 ,到y轴的距离是 ;
3.点C(2, -5)到x轴的距离是 ,到y轴的距离是 ;
4.点D (-2,-5)到x轴的距离是 ,到y轴的距离是 .
5
2
5
2
5
2
5
2
点P(a,b)到x轴的距离是 ,到y轴的距离是 .
︱b︱
︱a︱
探究平面内的点到坐标轴的距离
已知x轴上的P到y轴的距离为3,则点P的
坐标为__________________
(3,0)
或(-3,0)
例2 如图,正方形ABCD的边长为4,请建立一个平面直角坐标系,并写出正方形的四个顶点A,B,C,D在这个平面直角坐标系中的坐标.
A
B
C
D
建立平面直角坐标系表示图形的坐标
例2 如图,正方形ABCD的边长为4,请建立一个平面直角坐标系,并写出正方形的四个顶点A,B,C,D在这个平面直角坐标系中的坐标.
解:如图,以顶点A为原点,AB所在直线为x轴,AD所在直线为y轴建立平面直角坐标系.
A
B
C
D
此时,正方形的四个顶点A,B,C,D的坐标分别为:
x
y
A(0,0), B(4,0),
C(4,4),D(0,4).
O
例2,如图11-8,正方形ABCD的边长为4,请建立一个平面直角坐标系,并写出正方形的四个顶点A,B,C,D在这个平面直角坐标系中的坐标。
解:如图,以顶点C为原点,DC所在直线为x轴,BC所在直线为y轴建立平面直角坐标系。
A
B
C
D
此时,正方形的四个顶点A,B,C,D的坐标分别为:
x
y
A(-4,-4), B(0,-4),
C(0,0),D(-4,0).
O
A
B
C
D
x
y
O
由上得知,建立的平面直角坐标系不同,则各点的坐标也不同.你认为怎样建立直角坐标系才比较适当?
平面直角坐标系建立得适当,可以容易确定图形上的点,例如以正方形的两条边所在的直线为坐标轴,建立平面直角坐标系.又如可按图建立平面直角坐标系.
A
B
C
D
x
y
O
建立的平面直角坐标时,要记得标注x轴、y轴和坐标原点O.建立的平面直角坐标系不同,则各点的坐标也不同.
建立不同的平面直角坐标系,同一个点就会有不同的坐标,但正方形的形状和性质不会改变.
例.如图,已知△ABC在方格中,顶点A的坐标为(0,3).请在图中建立适当的平面直角坐标系,并根据所建立的平面直角坐标系写B,C的坐标.
A
B
C
解:
∵ 点A的横坐标为0,
∴ 点A在y轴上,
∵ 点A的纵坐标为3,
∴ 坐标原点在点A的正
下方且与点A的距离为3.
典型例析
A
B
C
解:
∵ 点A的横坐标为0,
∴ 点A在y轴上,
∵ 点A的纵坐标为3,
∴ 坐标原点在点A的正
下方且与点A的距离为3.
∴ 取过坐标原点的水平数轴为轴,向右为 正方
向,取过坐标原点的竖直数轴为y轴,向上为
正方向,建立平面直角坐标系,如图所示.
x
O
∴ 点B的坐标是(-3,-1),
点C的坐标是(1,1).
y
1.如图,建立适当的平面直角坐标系后,点B,C在这个平面直角坐标系中的坐标分别为(0,1),
(1,-1),则点A的坐标为( ).
A
B
C
练习巩固
A.(-1,2)
B.(2,-1)
C.(-2,1)
D.(1,-2)
A
2. 如图,在正方形ABCD中,已知点A,B,C的坐标分别是(1,1), (-1,1), (-1,-1), 则点D的坐标是 ( ).
A
B
C
D
A.(-1,0)
B.(1,0)
C.(1,-1)
D.(0,-2)
C
3. 已知点A(-4,3)和点B(-8,3),则点A,B之间的距离是 ( ).
A.3 B.4 C.8 D.12
B
4. 若点A(2,-4)和点B(a,-4)之间的距离是3,则a的值为 ( ).
A.3 B.5 C. -1 D.5或-1
D
5. 过点A(-1,-1)和点B(-1,5)作直线AB,则点AB ( ).
A.与y轴平行 B.与x轴平行 C.与y轴相交 D.无法确定
A
6. 已知点A的坐标为 (n+3,3),点B的坐标为(n-4,n),AB∥x轴,则AB的长为 ( ).
A.5 B.6 C. 7 D.13
C
7.如图,在5×4的方格纸中,每个小正方形边 长
为1,点O,A,B在方格纸的交点(格点)上,在
第四象限内的格点上找点C,使△ABC的面积
为3,则这样的点C共有( ).
A.2个 B.3个
C.4个 D.5个
A
B
x
y
B
图书馆
教学楼
旗杆
校门
实验楼
8.某学校的平面示意图如图所示,如果实验楼所在位置的坐标为(-2,-3) ,教学楼所在位置的坐标为(-1,2) ,请你建立坐标系,并写出图书馆,校门,旗杆的坐标.
x
y
O
图书馆,校门,旗杆的坐标分别是:
(-4,3), (-4,0),
(0,0).
解:
9.现有一张利用平面直角坐标系画出来的某
公园景区地图,如图所示,若知道游乐园D的坐标
为(2,-2).
(1)请按题意建立平面直角坐标系;
(2)写出其他景点的坐标;
(3)请指出哪个景点距离原点最近?
哪个景点距离原点最远?
(3)望春亭距离原点最近;牡丹园距离原点最远.
x
y
O
(-2,-1)
(-3,2)
(0,4)
(3,3)
雁塔
中心广场
钟楼
大成殿
科技大学
碑林
影月湖
如图,是某城市旅游景点的示意图.你是如何确定各个景点的位置的?
今天作业
课本P9页第4题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
