人教版数学八年级上册 11.1.2 三角形的高、中线与角平分线 教案
文档属性
| 名称 | 人教版数学八年级上册 11.1.2 三角形的高、中线与角平分线 教案 |  | |
| 格式 | docx | ||
| 文件大小 | 397.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-20 16:12:51 | ||
图片预览




文档简介
第十一章 三角形
11.1 与三角形有关的线段
11.1.2 三角形的高、中线与角平分线
第1课时 三角形的高、中线与角平分线
一、教学目标
【知识与技能】
1.了解三角形的高、中线、角平分线等有关概念;
2.会用工具准确画出三角形的高、中线、角平分线.
【过程与方法】
1.让学生经历画三角形的高、中线、角平分线过程,理解三角形的高、中线、角平分线的特点以及符号语言和图形语言的表达方法;
2.培养学生观察、分析、作图、解决问题的能力.
【情感、态度与价值观】
培养学生敢于实践操作、勇于发现、大胆探索、合作创新的精神.
二、课型
新授课
三、课时
第1课时
四、教学重难点
【教学重点】
三角形的高线、中线、角平分线的概念及画法.
【教学难点】
探究三角形的三条高线、三条角平分线、三条中线都交于一点的过程.
五、课前准备
教师:课件、三角尺、圆规、三角形木板等。
学生:三角尺、圆规、三角形纸板、小刀。
六、教学过程
(一)导入新课
1.动手操作,引出三角形高的概念
教师问1:我们前边学习过垂线、线段的中点、角平分线的定义,同学们还记得吗?
学生回答:
垂线:当两条直线相交所成的四个角中,有一个角是直角时,就说这两条直线互相垂直,其中一条直线叫做另一条直线的垂线
线段中点:把一条线段分成两条相等的线段的点
角平分线:一条射线把一个角分成两个相等的角,这条射线叫做这个角的平分线
教师总结后,出示课件2
教师问2:你还记得 “过一点画已知直线的垂线” 吗
如何做呢?
学生回答:放、靠、过、画(出示课件3)
教师问3:过三角形的一个顶点,你能画出它的对边的垂线吗
(二)探索新知
学生试着画出△ABC的边BC边上的高(出示课件5)
学生画出三角形所有的高,并观察这些高的特点.
教师问:根据画高的过程说明什么叫三角形的高?
学生讨论回答,教师完善并归纳.
教师总结:从三角形的一个顶点,向它的对边所在直线作垂线,顶点和垂足之间的线段叫做三角形的高线,简称三角形的高.
如下图, 线段AD是BC边上的高.
几何语言:AD⊥BC于点D,读作AD垂直BC于点D或∠ADC=∠ADB=90°.
(出示课件6)
教师问:在这些三角形中你能画出几条高?它们有什么相同点和不同点?
学生回答:每个三角形都能画出三条高.
相同点:三角形的三条高交于同一点.
不同点:锐角三角形的高交于三角形内一点,直角三角形的高交于直角的顶点,钝角三角形的高交于三角形外一点.(出示课件7-11)
教师问:如图所示,如果AD是△ABC的高,你能得到哪些结论?
学生回答,教师引导总结.(出示课件12)
三角形的三条高的特性:
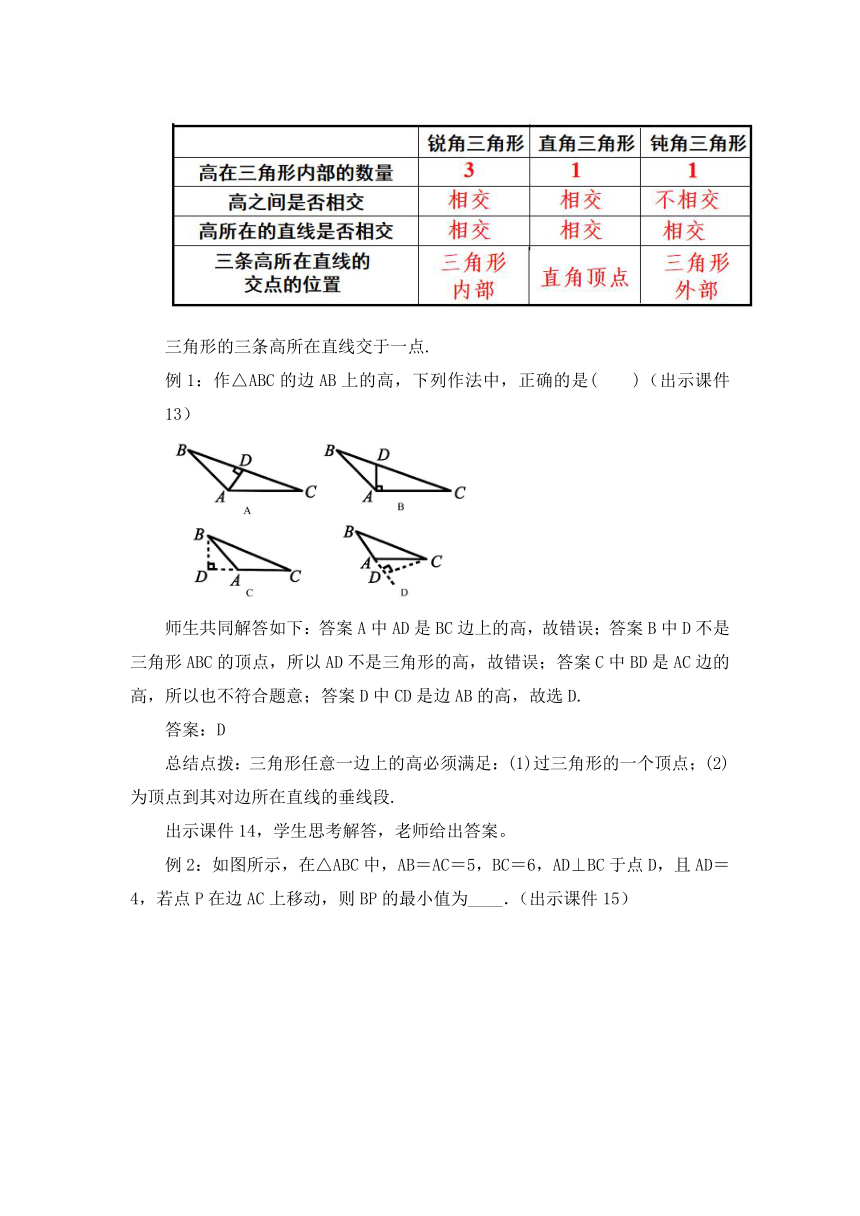
三角形的三条高所在直线交于一点.
例1:作△ABC的边AB上的高,下列作法中,正确的是( )(出示课件13)
师生共同解答如下:答案A中AD是BC边上的高,故错误;答案B中D不是三角形ABC的顶点,所以AD不是三角形的高,故错误;答案C中BD是AC边的高,所以也不符合题意;答案D中CD是边AB的高,故选D.
答案:D
总结点拨:三角形任意一边上的高必须满足:(1)过三角形的一个顶点;(2)为顶点到其对边所在直线的垂线段.
出示课件14,学生思考解答,老师给出答案。
例2:如图所示,在△ABC中,AB=AC=5,BC=6,AD⊥BC于点D,且AD=4,若点P在边AC上移动,则BP的最小值为____.(出示课件15)
师生共同解答如下:
当BP⊥AC时,BP的值最小.
∵S△ABC=BC·AD,S△ABC=AC·BP,
∴BC·AD=AC·BP ∴BC·AD=AC·BP
∴6×4=5BP, BP=,所以BP的最小值为。
总结点拨:
可利用面积相等作桥梁(但不求面积)求三角形的高, 此解题方法通常称为“面积法”.
出示课件16,学生思考解答,老师进行纠错改正。
2. 类比探索三角形的高的过程探索三角形的中线
教师问:如图,如果点C是线段AB的中点,你能得到什么结论?
学生回答:AC=BC=AB.
教师问:如图,如果点D是线段BC的中点,那么线段AD就称为△ABC的中线.类比三角形的高的概念,试说明什么叫三角形的中线?由三角形的中线能得到什么结论?
学生回答,教师总结.(出示课件18)
在三角形中,连接一个顶点与它对边的中点的线段叫做三角形的中线.
如图, 点D 是BC 的中点,则线段AD 是△ABC 的中线.
几何语言:BD =DC = BC.
教师问:如上图,画出△ABC 的另两条中线,观察三条中线,你有什么
发现?(出示课件19)
教师问:画出下列三角形的所有的中线,并讨论说明三角形的中线有什么特点?
学生作图并回答
三角形的三条中线相交于一点.
教师引导指点总结如下:
三角形的三条中线相交于一点,三角形三条中线的交点叫做三角形的重心.
教师问:如图所示,在△ABC中,AD是△ABC的中线,AE是△ABC的高.试判断△ABD和△ACD的面积有什么关系?为什么?
学生回答:△ABD和△ACD的面积相等,等低等高的三角形面积相等.
学生提问:你能发现什么规律?
学生回答:三角形的中线将三角形的面积平均分成两份.
教师总结:三角形的中线把三角形分成两个面积相等的三角形.(出示课件20)
教师小结如下(出示课件21)
1.定义:在三角形中,连接一个顶点和所对边的中点的线段叫做三角形的中线.
2.三角形的重心:三角形三条中线的交点.
3.三角形的重心在各三角形中的位置:在三角形内部.
4.三角形的任何一条中线把三角形分成面积相等的两个三角形.如上图:AD为中线,则S△ABD=S△ACD.
5.三角形任何一边上的中线把三角形分成的两个小三角形周长之差等于原三角形长边与短边之差.△ABD的周长–△ACD的周长=AB–AC.
例3:如图所示,AD是△ABC的中线,已知△ABD的周长为25 cm,AB比AC长6 cm,则△ACD的周长为( )(出示课件21)
A.19 cm B.22 cm C.25 cm D.31 cm
师生共同解答如下:
解:∵AD是BC边上的中线,
∴BD=CD,
∴△ABD和△ACD周长的差=(AB+BD+AD)–(AC+CD+AD)=AB –AC.
∵△ABD的周长为25 cm,AB比AC长6 cm,
∴△ACD的周长为25–6=19(cm).
故选A.
3. 通过类比的方法探究三角形的角平分线
教师问:如图,若OC是∠AOB的平分线,你能得到什么结论?
学生回答:∠AOC=∠BOC=∠AOB.
教师问:如果这个角是三角形的一个内角?请同学们在一张薄纸上任意画一个三角形,你能设法画出它的一个内角的平分线吗 你能通过折纸的方法得到它吗
学生操作并回答(出示课件25)
(1)用量角器画最简便,用圆规也能
(2)在一张纸上画出一个三角形并剪下,将它的一个角对折,使其两边重合.
折痕AD即为三角形的∠A的平分线.
教师问:如图,在△ABC中,如果∠BAC的平分线AD交BC边于点D,我们就称AD是△ABC的角平分线.如何给三角形的角平分线下一个定义呢?
学生回答:平分三角形一个内角的线段叫做三角形的角平分线.
教师总结如下:
三角形的角平分线的定义:在三角形中,一个内角的平分线与它的对边相交,这个角的顶点与交点之间的线段叫三角形的角平分线.
几何语言:∠1=∠2= ∠BAC
警示:“三角形的角平分线”是一条线段.
做一做:
每人准备锐角三角形、钝角三角形和直角三角形纸片各一个.分别画出这三个三角形的三条角平分线。
教师问:你能用折纸的办法得到它们吗 在每个三角形中,这三条角平分线之间有怎样的位置关系
学生回答:三角形共有三条内角平分线,它们交于三角形内一点.(出示课件28)
学生问:三角形的角平分线与角的角平分线相同吗?为什么?
学生回答,教师归纳并总结.
三角形的角平分线与角平分线不相同,角平分线是一条射线,三角形的角平分线是一条线段.
例4:如图,在△ABC中,∠BAC=68°,∠B=36°,AD是△ABC的一条角平分线,求∠ADB的度数.
(出示课件29)
师生共同解答如下:
解:∵AD是△ABC的角平分线,∠BAC=68°,
∴∠DAC=∠BAD=34°.
在△ABD中,∠B+∠ADB+∠BAD=180°,
∴∠ADB=180°–∠B–∠BAD
=180°–36°–34°
=110°.
(三)课堂练习(出示课件34-40)
1.下列说法正确的是( )
A.三角形三条高都在三角形内
B.三角形三条中线相交于一点
C.三角形的三条角平分线可能在三角形内,也可能在三角形外
D.三角形的角平分线是射线
2.在△ABC中,AD为中线,BE为角平分线,则在以下等式中:①∠BAD=∠CAD;②∠ABE=∠CBE;③BD=DC;
④AE=EC.其中正确的是 ( )
A.①② B.③④ C.①④ D.②③
3. 如图,△ABC中∠C=90°,CD⊥AB,图中线段中可以作为△ABC的高的有( )
A.2条 B.3条 C.4条 D.5条
4. 下列各组图形中,哪一组图形中AD是△ABC 的BC边上的高 ( )
5.填空:
(1)如图①,AD,BE,CF是△ABC的三条中线,则AB= 2__,BD= __,AE= ___.
(2)如图②,AD,BE,CF是△ABC的三条角平分线,则∠1= __, ∠3=_________, ∠ACB=2______.
6. 在ΔABC中,CD是中线,已知BC–AC=5cm,ΔDBC的周长为25cm,求ΔADC的周长.
7. 如图,在△ABC中,AD是△ABC的高,AE是 △ABC的角平分线,已知∠BAC=82°,∠C=40°,求∠DAE的大小.
参考答案:
1.B
2.D
3.B
4.D
5.(1)AF DC AC (2)∠2 ∠ABC ∠4
6. 解:∵CD是△ABC的中线,
∴BD=AD,
∴△DBC的周长=BC+BD+CD=25cm,
则BD+CD=25–BC.
∴△ADC的周长=AD+CD+AC
=BD+CD+AC
=25–BC+AC
=25–(BC–AC)=25–5=20cm.
7. 解: ∵ AD是△ABC的高,∴∠ADC=90°.
∵ ∠ADC+∠C+∠DAC=180°,
∴ ∠DAC=180°–(∠ADC+∠C )
=180°–90°–40°=50°.
∵AE是△ABC的角平分线,且∠BAC=82°,
∴∠CAE=41°,
∴∠DAE=∠DAC–∠CAE=50°–41°= 9°.
(四)课堂小结
今天我们学了哪些内容:
三角形的重要线段 概念 图形 表示法 数量及交点位置
三角形的高线 从三角形的一个顶点向它的对边所在的直线作垂线,顶点和垂足之间的线段 ∵AD是△ABC的高线. ∴AD⊥BC,∠ADB=∠ADC=90°. 3条高,锐角三角形:形内;钝角三角形:形外;直角三角形:直角顶点
三角形的中线 三角形中,连结一个顶点和它对边中的线段 ∵AD是△ABC的BC上的中线, ∴BD=CD= BC 3条,交点叫作三角形的重心.形内
三角形的角平分线 三角形一个内角的平分线与它的对边相交,这个角顶点与交点之间的线段 ∵AD是△ABC的∠BAC的平分线, ∴∠1=∠2= ∠BAC 3条,形内.
(五)课前预习
预习下节课(11.1.3)的相关内容。
知道三角形稳定性,了解三角形稳定在生活中的应用
七、课后作业
1、教材5页练习1,2
2、如图,△ABC中,AD是BC边上的高,AE、BF分别是∠BAC、∠ABC的平分线,∠BAC=50°,∠ABC=60°,则∠EAD+∠ACD=( )
A.75° B.80° C.85° D.90°
八、板书设计:
九、教学反思:
本节内容主要介绍三角形的高、中线和角平分线的概念及基本性质,重点是性质的应用.教师要引导学生从熟悉的知识入手,并利用类比的方法自主探索新的知识.在教学过程中,让学生以独立思考为主,并在必要时进行互助交流,让学生经历得出结论的过程,培养学生解决问题的能力.
11.1 与三角形有关的线段
11.1.2 三角形的高、中线与角平分线
第1课时 三角形的高、中线与角平分线
一、教学目标
【知识与技能】
1.了解三角形的高、中线、角平分线等有关概念;
2.会用工具准确画出三角形的高、中线、角平分线.
【过程与方法】
1.让学生经历画三角形的高、中线、角平分线过程,理解三角形的高、中线、角平分线的特点以及符号语言和图形语言的表达方法;
2.培养学生观察、分析、作图、解决问题的能力.
【情感、态度与价值观】
培养学生敢于实践操作、勇于发现、大胆探索、合作创新的精神.
二、课型
新授课
三、课时
第1课时
四、教学重难点
【教学重点】
三角形的高线、中线、角平分线的概念及画法.
【教学难点】
探究三角形的三条高线、三条角平分线、三条中线都交于一点的过程.
五、课前准备
教师:课件、三角尺、圆规、三角形木板等。
学生:三角尺、圆规、三角形纸板、小刀。
六、教学过程
(一)导入新课
1.动手操作,引出三角形高的概念
教师问1:我们前边学习过垂线、线段的中点、角平分线的定义,同学们还记得吗?
学生回答:
垂线:当两条直线相交所成的四个角中,有一个角是直角时,就说这两条直线互相垂直,其中一条直线叫做另一条直线的垂线
线段中点:把一条线段分成两条相等的线段的点
角平分线:一条射线把一个角分成两个相等的角,这条射线叫做这个角的平分线
教师总结后,出示课件2
教师问2:你还记得 “过一点画已知直线的垂线” 吗
如何做呢?
学生回答:放、靠、过、画(出示课件3)
教师问3:过三角形的一个顶点,你能画出它的对边的垂线吗
(二)探索新知
学生试着画出△ABC的边BC边上的高(出示课件5)
学生画出三角形所有的高,并观察这些高的特点.
教师问:根据画高的过程说明什么叫三角形的高?
学生讨论回答,教师完善并归纳.
教师总结:从三角形的一个顶点,向它的对边所在直线作垂线,顶点和垂足之间的线段叫做三角形的高线,简称三角形的高.
如下图, 线段AD是BC边上的高.
几何语言:AD⊥BC于点D,读作AD垂直BC于点D或∠ADC=∠ADB=90°.
(出示课件6)
教师问:在这些三角形中你能画出几条高?它们有什么相同点和不同点?
学生回答:每个三角形都能画出三条高.
相同点:三角形的三条高交于同一点.
不同点:锐角三角形的高交于三角形内一点,直角三角形的高交于直角的顶点,钝角三角形的高交于三角形外一点.(出示课件7-11)
教师问:如图所示,如果AD是△ABC的高,你能得到哪些结论?
学生回答,教师引导总结.(出示课件12)
三角形的三条高的特性:
三角形的三条高所在直线交于一点.
例1:作△ABC的边AB上的高,下列作法中,正确的是( )(出示课件13)
师生共同解答如下:答案A中AD是BC边上的高,故错误;答案B中D不是三角形ABC的顶点,所以AD不是三角形的高,故错误;答案C中BD是AC边的高,所以也不符合题意;答案D中CD是边AB的高,故选D.
答案:D
总结点拨:三角形任意一边上的高必须满足:(1)过三角形的一个顶点;(2)为顶点到其对边所在直线的垂线段.
出示课件14,学生思考解答,老师给出答案。
例2:如图所示,在△ABC中,AB=AC=5,BC=6,AD⊥BC于点D,且AD=4,若点P在边AC上移动,则BP的最小值为____.(出示课件15)
师生共同解答如下:
当BP⊥AC时,BP的值最小.
∵S△ABC=BC·AD,S△ABC=AC·BP,
∴BC·AD=AC·BP ∴BC·AD=AC·BP
∴6×4=5BP, BP=,所以BP的最小值为。
总结点拨:
可利用面积相等作桥梁(但不求面积)求三角形的高, 此解题方法通常称为“面积法”.
出示课件16,学生思考解答,老师进行纠错改正。
2. 类比探索三角形的高的过程探索三角形的中线
教师问:如图,如果点C是线段AB的中点,你能得到什么结论?
学生回答:AC=BC=AB.
教师问:如图,如果点D是线段BC的中点,那么线段AD就称为△ABC的中线.类比三角形的高的概念,试说明什么叫三角形的中线?由三角形的中线能得到什么结论?
学生回答,教师总结.(出示课件18)
在三角形中,连接一个顶点与它对边的中点的线段叫做三角形的中线.
如图, 点D 是BC 的中点,则线段AD 是△ABC 的中线.
几何语言:BD =DC = BC.
教师问:如上图,画出△ABC 的另两条中线,观察三条中线,你有什么
发现?(出示课件19)
教师问:画出下列三角形的所有的中线,并讨论说明三角形的中线有什么特点?
学生作图并回答
三角形的三条中线相交于一点.
教师引导指点总结如下:
三角形的三条中线相交于一点,三角形三条中线的交点叫做三角形的重心.
教师问:如图所示,在△ABC中,AD是△ABC的中线,AE是△ABC的高.试判断△ABD和△ACD的面积有什么关系?为什么?
学生回答:△ABD和△ACD的面积相等,等低等高的三角形面积相等.
学生提问:你能发现什么规律?
学生回答:三角形的中线将三角形的面积平均分成两份.
教师总结:三角形的中线把三角形分成两个面积相等的三角形.(出示课件20)
教师小结如下(出示课件21)
1.定义:在三角形中,连接一个顶点和所对边的中点的线段叫做三角形的中线.
2.三角形的重心:三角形三条中线的交点.
3.三角形的重心在各三角形中的位置:在三角形内部.
4.三角形的任何一条中线把三角形分成面积相等的两个三角形.如上图:AD为中线,则S△ABD=S△ACD.
5.三角形任何一边上的中线把三角形分成的两个小三角形周长之差等于原三角形长边与短边之差.△ABD的周长–△ACD的周长=AB–AC.
例3:如图所示,AD是△ABC的中线,已知△ABD的周长为25 cm,AB比AC长6 cm,则△ACD的周长为( )(出示课件21)
A.19 cm B.22 cm C.25 cm D.31 cm
师生共同解答如下:
解:∵AD是BC边上的中线,
∴BD=CD,
∴△ABD和△ACD周长的差=(AB+BD+AD)–(AC+CD+AD)=AB –AC.
∵△ABD的周长为25 cm,AB比AC长6 cm,
∴△ACD的周长为25–6=19(cm).
故选A.
3. 通过类比的方法探究三角形的角平分线
教师问:如图,若OC是∠AOB的平分线,你能得到什么结论?
学生回答:∠AOC=∠BOC=∠AOB.
教师问:如果这个角是三角形的一个内角?请同学们在一张薄纸上任意画一个三角形,你能设法画出它的一个内角的平分线吗 你能通过折纸的方法得到它吗
学生操作并回答(出示课件25)
(1)用量角器画最简便,用圆规也能
(2)在一张纸上画出一个三角形并剪下,将它的一个角对折,使其两边重合.
折痕AD即为三角形的∠A的平分线.
教师问:如图,在△ABC中,如果∠BAC的平分线AD交BC边于点D,我们就称AD是△ABC的角平分线.如何给三角形的角平分线下一个定义呢?
学生回答:平分三角形一个内角的线段叫做三角形的角平分线.
教师总结如下:
三角形的角平分线的定义:在三角形中,一个内角的平分线与它的对边相交,这个角的顶点与交点之间的线段叫三角形的角平分线.
几何语言:∠1=∠2= ∠BAC
警示:“三角形的角平分线”是一条线段.
做一做:
每人准备锐角三角形、钝角三角形和直角三角形纸片各一个.分别画出这三个三角形的三条角平分线。
教师问:你能用折纸的办法得到它们吗 在每个三角形中,这三条角平分线之间有怎样的位置关系
学生回答:三角形共有三条内角平分线,它们交于三角形内一点.(出示课件28)
学生问:三角形的角平分线与角的角平分线相同吗?为什么?
学生回答,教师归纳并总结.
三角形的角平分线与角平分线不相同,角平分线是一条射线,三角形的角平分线是一条线段.
例4:如图,在△ABC中,∠BAC=68°,∠B=36°,AD是△ABC的一条角平分线,求∠ADB的度数.
(出示课件29)
师生共同解答如下:
解:∵AD是△ABC的角平分线,∠BAC=68°,
∴∠DAC=∠BAD=34°.
在△ABD中,∠B+∠ADB+∠BAD=180°,
∴∠ADB=180°–∠B–∠BAD
=180°–36°–34°
=110°.
(三)课堂练习(出示课件34-40)
1.下列说法正确的是( )
A.三角形三条高都在三角形内
B.三角形三条中线相交于一点
C.三角形的三条角平分线可能在三角形内,也可能在三角形外
D.三角形的角平分线是射线
2.在△ABC中,AD为中线,BE为角平分线,则在以下等式中:①∠BAD=∠CAD;②∠ABE=∠CBE;③BD=DC;
④AE=EC.其中正确的是 ( )
A.①② B.③④ C.①④ D.②③
3. 如图,△ABC中∠C=90°,CD⊥AB,图中线段中可以作为△ABC的高的有( )
A.2条 B.3条 C.4条 D.5条
4. 下列各组图形中,哪一组图形中AD是△ABC 的BC边上的高 ( )
5.填空:
(1)如图①,AD,BE,CF是△ABC的三条中线,则AB= 2__,BD= __,AE= ___.
(2)如图②,AD,BE,CF是△ABC的三条角平分线,则∠1= __, ∠3=_________, ∠ACB=2______.
6. 在ΔABC中,CD是中线,已知BC–AC=5cm,ΔDBC的周长为25cm,求ΔADC的周长.
7. 如图,在△ABC中,AD是△ABC的高,AE是 △ABC的角平分线,已知∠BAC=82°,∠C=40°,求∠DAE的大小.
参考答案:
1.B
2.D
3.B
4.D
5.(1)AF DC AC (2)∠2 ∠ABC ∠4
6. 解:∵CD是△ABC的中线,
∴BD=AD,
∴△DBC的周长=BC+BD+CD=25cm,
则BD+CD=25–BC.
∴△ADC的周长=AD+CD+AC
=BD+CD+AC
=25–BC+AC
=25–(BC–AC)=25–5=20cm.
7. 解: ∵ AD是△ABC的高,∴∠ADC=90°.
∵ ∠ADC+∠C+∠DAC=180°,
∴ ∠DAC=180°–(∠ADC+∠C )
=180°–90°–40°=50°.
∵AE是△ABC的角平分线,且∠BAC=82°,
∴∠CAE=41°,
∴∠DAE=∠DAC–∠CAE=50°–41°= 9°.
(四)课堂小结
今天我们学了哪些内容:
三角形的重要线段 概念 图形 表示法 数量及交点位置
三角形的高线 从三角形的一个顶点向它的对边所在的直线作垂线,顶点和垂足之间的线段 ∵AD是△ABC的高线. ∴AD⊥BC,∠ADB=∠ADC=90°. 3条高,锐角三角形:形内;钝角三角形:形外;直角三角形:直角顶点
三角形的中线 三角形中,连结一个顶点和它对边中的线段 ∵AD是△ABC的BC上的中线, ∴BD=CD= BC 3条,交点叫作三角形的重心.形内
三角形的角平分线 三角形一个内角的平分线与它的对边相交,这个角顶点与交点之间的线段 ∵AD是△ABC的∠BAC的平分线, ∴∠1=∠2= ∠BAC 3条,形内.
(五)课前预习
预习下节课(11.1.3)的相关内容。
知道三角形稳定性,了解三角形稳定在生活中的应用
七、课后作业
1、教材5页练习1,2
2、如图,△ABC中,AD是BC边上的高,AE、BF分别是∠BAC、∠ABC的平分线,∠BAC=50°,∠ABC=60°,则∠EAD+∠ACD=( )
A.75° B.80° C.85° D.90°
八、板书设计:
九、教学反思:
本节内容主要介绍三角形的高、中线和角平分线的概念及基本性质,重点是性质的应用.教师要引导学生从熟悉的知识入手,并利用类比的方法自主探索新的知识.在教学过程中,让学生以独立思考为主,并在必要时进行互助交流,让学生经历得出结论的过程,培养学生解决问题的能力.
