第六章 平面图形的认识(一)重难点检测卷-小升初衔接数学试卷苏科版(预习资料)
文档属性
| 名称 | 第六章 平面图形的认识(一)重难点检测卷-小升初衔接数学试卷苏科版(预习资料) |  | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-22 10:00:25 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第七章平面图形的认识(一)重难点检测卷-小升初衔接数学试卷苏科版(预习资料)
一、单选题
1.钟表4点30分时,时针与分针所成的角的度数为( )
A.45° B.30° C.60° D.75°
2.木匠在木料上画线,先确定两个点的位置,就能把线画得很准确,其依据是( )
A.两点之间线段最短
B.过一点有无数条直线
C.两点确定一条直线
D.两点之间线段的长度叫做这两点之间的距离
3.如图,码头A在码头B的正西方向,甲、乙两船分别从A,B同时出发,并以等速驶向某海域,甲的航向是北偏东35°,为避免行进中甲、乙相撞,则乙的航向不能是( )
A.北偏西55° B.北偏东65° C.北偏东35° D.北偏西35°
4.如图,一副三角板(直角顶点重合)摆放在桌面上,若 ,则 等于( )
A. B. C. D.
5.为了让一队学生站成一条直线,先让两名学生站好不动,其他学生依次往后站,要求目视前方只能看到各自前面的那名学生,这种做法运用的数学知识是( )
A.两点确定一条直线 B.两点之间,线段最短
C.射线只有一个端点 D.过一点有无数条直线
6.如图,观察图形,下列结论中不正确的是( )
A.图中有 条线段
B.直线 和直线 是同一条直线
C.
D.射线 和射线 是同一条射线
7.一个角的度数等于,那么它的余角等于( )
A. B. C. D.
8.关于角的描述不正确的是( )
A.∠1与∠AOB表示同一个角 B.∠AOC可以用∠O表示
C.∠AOC=∠AOB+∠BOC D.∠β表示∠BOC
二、填空题
9.11°27′= °.
10.如图,直线AB、CD相交于点O, ,那么 .
11.如图, 的度数是 .
12.已知 , 比较这两个角的大小, 结果为∠1 △2.
13.下列说法:①两点之间,线段最短.②射线和射线是同一条射线.③连接两点的线段的长度叫做这两点间的距离.其中正确的序号是 .
14.若,,则与的关系是 .(填“互余”或“互补”)
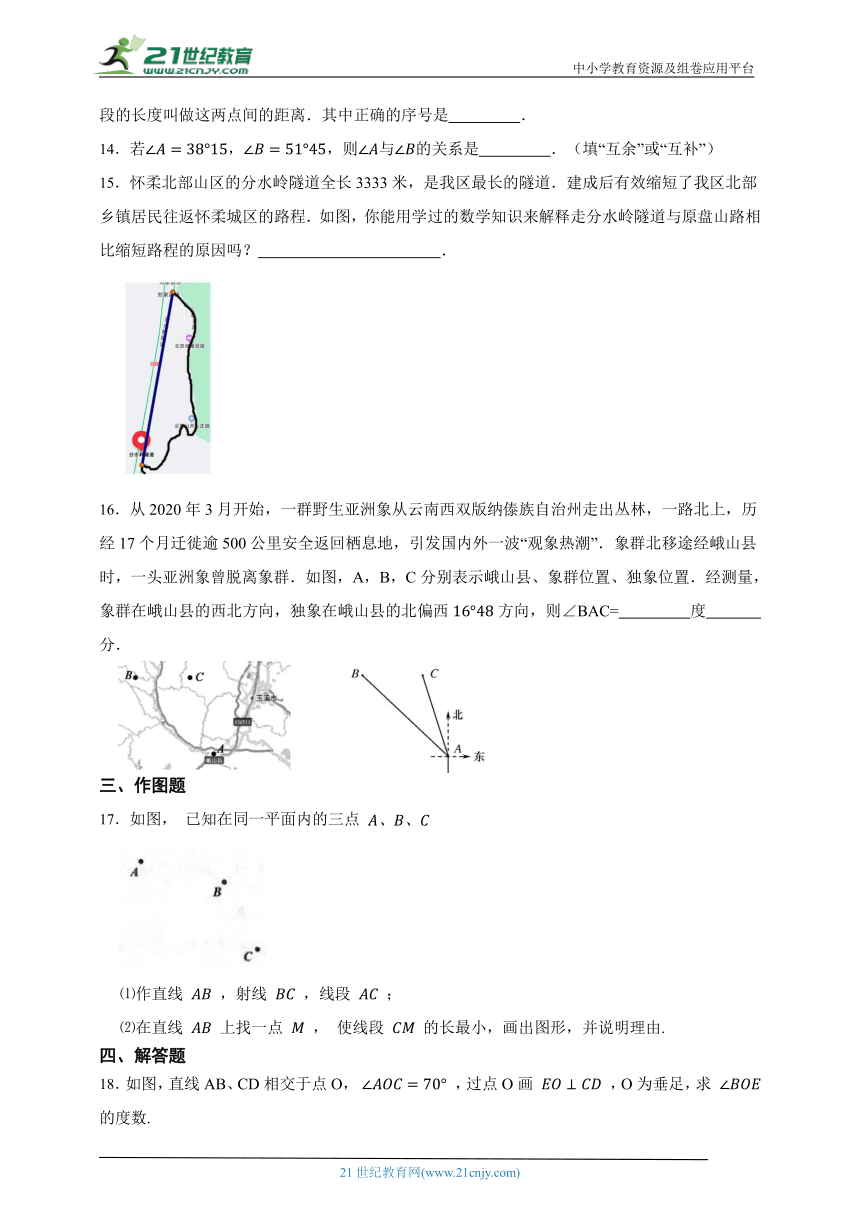
15.怀柔北部山区的分水岭隧道全长3333米,是我区最长的隧道.建成后有效缩短了我区北部乡镇居民往返怀柔城区的路程.如图,你能用学过的数学知识来解释走分水岭隧道与原盘山路相比缩短路程的原因吗? .
16.从2020年3月开始,一群野生亚洲象从云南西双版纳傣族自治州走出丛林,一路北上,历经17个月迁徙逾500公里安全返回栖息地,引发国内外一波“观象热潮”.象群北移途经峨山县时,一头亚洲象曾脱离象群.如图,A,B,C分别表示峨山县、象群位置、独象位置.经测量,象群在峨山县的西北方向,独象在峨山县的北偏西方向,则∠BAC= 度 分.
三、作图题
17.如图, 已知在同一平面内的三点
⑴作直线 ,射线 ,线段 ;
⑵在直线 上找一点 , 使线段 的长最小,画出图形,并说明理由.
四、解答题
18.如图,直线AB、CD相交于点O, ,过点O画 ,O为垂足,求 的度数.
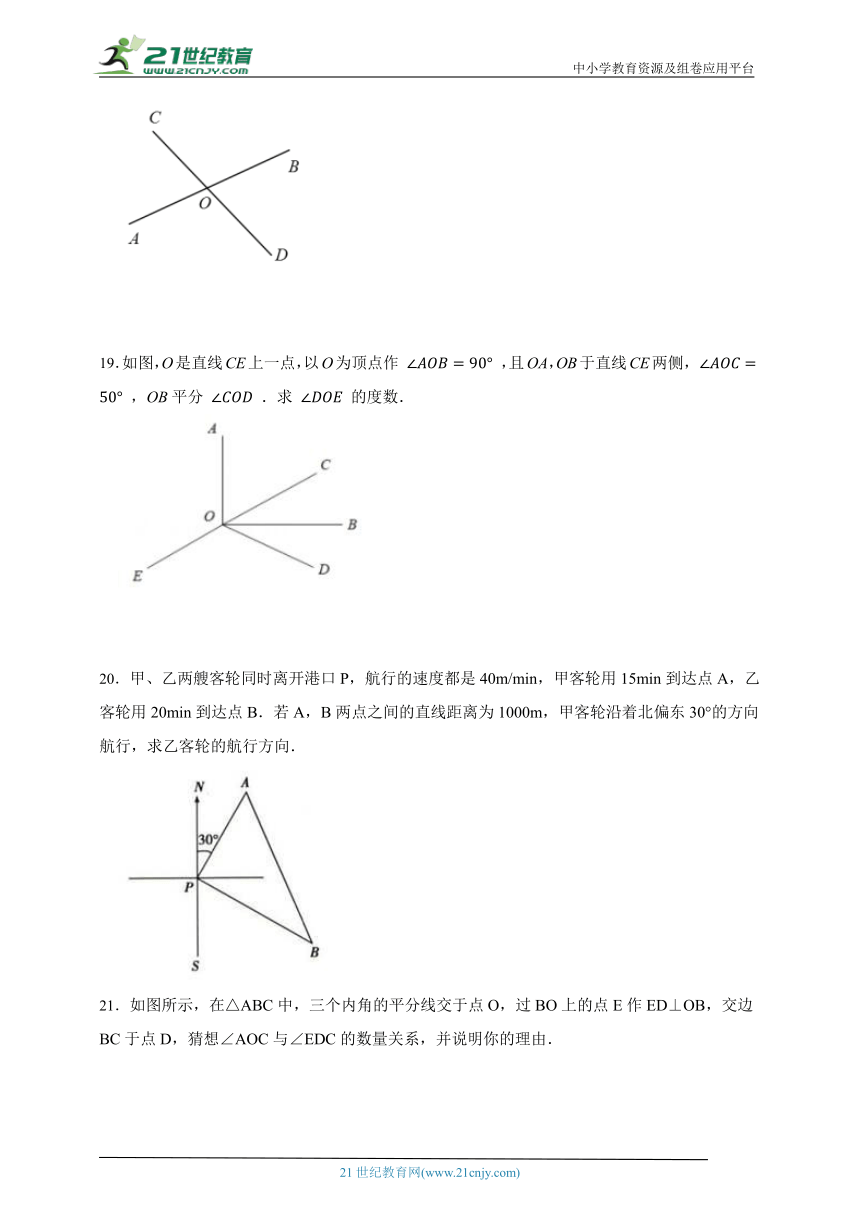
19.如图,O是直线CE上一点,以O为顶点作 ,且OA,OB于直线CE两侧, ,OB平分 .求 的度数.
20.甲、乙两艘客轮同时离开港口P,航行的速度都是40m/min,甲客轮用15min到达点A,乙客轮用20min到达点B.若A,B两点之间的直线距离为1000m,甲客轮沿着北偏东30°的方向航行,求乙客轮的航行方向.
21.如图所示,在△ABC中,三个内角的平分线交于点O,过BO上的点E作ED⊥OB,交边BC于点D,猜想∠AOC与∠EDC的数量关系,并说明你的理由.
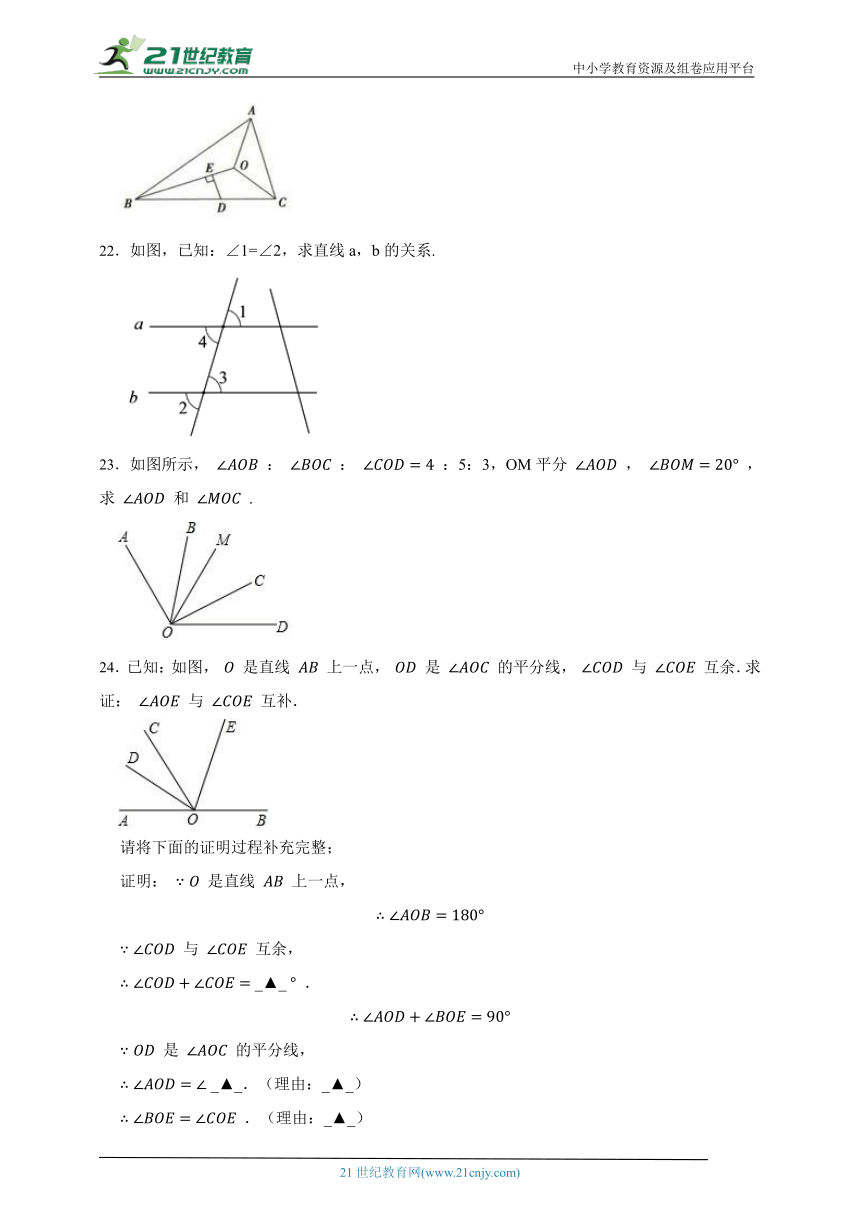
22.如图,已知:∠1=∠2,求直线a,b的关系.
23.如图所示, : : :5:3,OM平分 , ,求 和 .
24.已知:如图, 是直线 上一点, 是 的平分线, 与 互余.求证: 与 互补.
请将下面的证明过程补充完整;
证明: 是直线 上一点,
与 互余,
_▲_ .
是 的平分线,
_▲_.(理由:_▲_)
.(理由:_▲_)
_▲_ .
与 互补.
五、综合题
25.如图1,某校七年级数学学习小组在课后综合实践活动中,把一个直角三角尺AOB的直角顶点O放在互相垂直的两条直线PQ、MN的垂足O处,并使两条直角边落在直线PQ、MN上,将△AOB绕着点O顺时针旋转α°(0°<α<180°) .
(1)如图2,若α=26°,则∠BOP= ,∠AOM+∠BOQ= .
(2)若射线OC是∠BOM的角平分线,且∠POC=β°
①若△AOB旋转到图3的位置,∠BON的度数为多少?(用含β的代数式表示)
②△AOB在旋转过程中,若∠AOC=2∠AOM,求此时β的值.
答案解析部分
1.【答案】A
2.【答案】C
3.【答案】D
4.【答案】B
5.【答案】A
6.【答案】A
7.【答案】D
8.【答案】B
9.【答案】11.45
10.【答案】59.4
11.【答案】35
12.【答案】<
13.【答案】①③
14.【答案】互余
15.【答案】两点之间,线段最短
16.【答案】28;12
17.【答案】解:如图
18.【答案】解:如图:
∵∠AOC=70°,
∴∠BOC=180°-70°=110°,
∵EO⊥CD,
∴∠BOE=∠BOC-∠COE=20°;
如图,
∵∠AOC=70°,
∴∠BOD=70°,
∵EO⊥CD,
∴∠BOE=∠BOD+∠DOE=160°;
综上:∠BOE的度数为20°或160°.
19.【答案】解:∠BOC=∠AOB-∠AOC
=90°-50°
=40°,
∵ OB平分 ,
∴∠COD=2∠BOC=80°,
∴∠DOE=180°-∠COD=100°.
20.【答案】解:由题意,得PA= 40×15= 600(m),PB=40× 20= 800(m),
AB=1 000 m.
∵PA2+ PB2 = 6002+ 8002=1 0002=AB2,
∴△APB为直角三角形,∠APB= 90°.
∵∠NPA= =30° ,所以∠SPB= 60°,
∴乙客轮的航行方向为南偏东60°.
21.【答案】解:∠AOC=∠EDC.理由如下:
∵△ABC的三个内角的平分线交于点O,
∴∠OAC= ∠BAC,∠OCA= ∠ACB,∠OBC= ∠ABC.
∴∠AOC= 180°-(∠OAC+∠OCA)=180°- (∠BAC+∠BCA)=180°- (180°-∠ABC)=90°+ ∠ABC=90°+∠OBC.
∵DE⊥OB,所以∠BED= 90°.
∴∠EDC= 180°-∠EDB=∠OBC+∠BED= 90°+∠OBC.
∴∠AOC=∠EDC.
22.【答案】解:∵∠1=∠4,∠2=∠3(对顶角相等)
又∠1=∠2(已知)
所以∠3=∠4(等量代换)
∴a//b(内错角相等,两直线平行)
23.【答案】解:设 , , ,
,
平分 ,
,
,
,
解得: ,
, ,
.
24.【答案】证明:∵O是直线AB上一点
∴∠AOB=180°
∵∠COD与∠COE互余
∴∠COD+∠COE=90°
∴∠AOD+∠BOE=90°
∵OD是∠AOC的平分线
∴∠AOD=∠COD(理由:角平分线的定义)
∴∠BOE=∠COE(理由:等式性质)
∵∠AOE+∠BOE=180°
∴∠AOE+∠COE=180°
∴∠AOE与∠COE互补.
故答案为:90;COD; 角平分线的定义;等式性质,180.
25.【答案】(1)64°;180°
(2)①∵∠MOP=90°,∠POC=β°,
∴∠MOC=90°-β°,
∵OC是∠BOM的角平分线,
∴∠MOB=2∠MOC=180°-2β°,
∴∠BOP=90°-∠MOB=90°-(180°-2β°)=2β°-90°,
∵∠PON=90°,
∴∠BON=∠BOP+∠PON=2β°-90°+90°=2β°;
②如图,当OB旋转到OP的左侧时,
∵OC是∠BOM的角平分线,
∴∠COB=∠MOC,
∵∠AOC=2∠AOM,
∴∠AOM=∠MOC,
∴∠COB=∠MOC=∠AOM,
∵∠COB+∠MOC+∠AOM=90°,
∴∠COB=∠MOC=∠AOM=30°,
∴∠POC=β°=90°-∠MOC=90°-30°=60°,
②如图,当OB旋转到OP的右侧时,
设∠AOM=x,
∵∠AOC=2∠AOM=2x,
∴∠MOC=3∠AOM=3x,
∵∠COB+∠MOC+∠AOM=90°,
∴∠COB=∠MOC=∠AOM=30°,
∵OC是∠BOM的角平分线,
∴∠COB=∠MOC=3x,
∴∠AOB=∠AOC+∠BOC=5x=90°,
∴x=18°,
∴∠MOC=3x=54°,
∴∠POC=β°=90°-∠MOC=90°-54°=36°,
综上,β的值为60°或36°.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第七章平面图形的认识(一)重难点检测卷-小升初衔接数学试卷苏科版(预习资料)
一、单选题
1.钟表4点30分时,时针与分针所成的角的度数为( )
A.45° B.30° C.60° D.75°
2.木匠在木料上画线,先确定两个点的位置,就能把线画得很准确,其依据是( )
A.两点之间线段最短
B.过一点有无数条直线
C.两点确定一条直线
D.两点之间线段的长度叫做这两点之间的距离
3.如图,码头A在码头B的正西方向,甲、乙两船分别从A,B同时出发,并以等速驶向某海域,甲的航向是北偏东35°,为避免行进中甲、乙相撞,则乙的航向不能是( )
A.北偏西55° B.北偏东65° C.北偏东35° D.北偏西35°
4.如图,一副三角板(直角顶点重合)摆放在桌面上,若 ,则 等于( )
A. B. C. D.
5.为了让一队学生站成一条直线,先让两名学生站好不动,其他学生依次往后站,要求目视前方只能看到各自前面的那名学生,这种做法运用的数学知识是( )
A.两点确定一条直线 B.两点之间,线段最短
C.射线只有一个端点 D.过一点有无数条直线
6.如图,观察图形,下列结论中不正确的是( )
A.图中有 条线段
B.直线 和直线 是同一条直线
C.
D.射线 和射线 是同一条射线
7.一个角的度数等于,那么它的余角等于( )
A. B. C. D.
8.关于角的描述不正确的是( )
A.∠1与∠AOB表示同一个角 B.∠AOC可以用∠O表示
C.∠AOC=∠AOB+∠BOC D.∠β表示∠BOC
二、填空题
9.11°27′= °.
10.如图,直线AB、CD相交于点O, ,那么 .
11.如图, 的度数是 .
12.已知 , 比较这两个角的大小, 结果为∠1 △2.
13.下列说法:①两点之间,线段最短.②射线和射线是同一条射线.③连接两点的线段的长度叫做这两点间的距离.其中正确的序号是 .
14.若,,则与的关系是 .(填“互余”或“互补”)
15.怀柔北部山区的分水岭隧道全长3333米,是我区最长的隧道.建成后有效缩短了我区北部乡镇居民往返怀柔城区的路程.如图,你能用学过的数学知识来解释走分水岭隧道与原盘山路相比缩短路程的原因吗? .
16.从2020年3月开始,一群野生亚洲象从云南西双版纳傣族自治州走出丛林,一路北上,历经17个月迁徙逾500公里安全返回栖息地,引发国内外一波“观象热潮”.象群北移途经峨山县时,一头亚洲象曾脱离象群.如图,A,B,C分别表示峨山县、象群位置、独象位置.经测量,象群在峨山县的西北方向,独象在峨山县的北偏西方向,则∠BAC= 度 分.
三、作图题
17.如图, 已知在同一平面内的三点
⑴作直线 ,射线 ,线段 ;
⑵在直线 上找一点 , 使线段 的长最小,画出图形,并说明理由.
四、解答题
18.如图,直线AB、CD相交于点O, ,过点O画 ,O为垂足,求 的度数.
19.如图,O是直线CE上一点,以O为顶点作 ,且OA,OB于直线CE两侧, ,OB平分 .求 的度数.
20.甲、乙两艘客轮同时离开港口P,航行的速度都是40m/min,甲客轮用15min到达点A,乙客轮用20min到达点B.若A,B两点之间的直线距离为1000m,甲客轮沿着北偏东30°的方向航行,求乙客轮的航行方向.
21.如图所示,在△ABC中,三个内角的平分线交于点O,过BO上的点E作ED⊥OB,交边BC于点D,猜想∠AOC与∠EDC的数量关系,并说明你的理由.
22.如图,已知:∠1=∠2,求直线a,b的关系.
23.如图所示, : : :5:3,OM平分 , ,求 和 .
24.已知:如图, 是直线 上一点, 是 的平分线, 与 互余.求证: 与 互补.
请将下面的证明过程补充完整;
证明: 是直线 上一点,
与 互余,
_▲_ .
是 的平分线,
_▲_.(理由:_▲_)
.(理由:_▲_)
_▲_ .
与 互补.
五、综合题
25.如图1,某校七年级数学学习小组在课后综合实践活动中,把一个直角三角尺AOB的直角顶点O放在互相垂直的两条直线PQ、MN的垂足O处,并使两条直角边落在直线PQ、MN上,将△AOB绕着点O顺时针旋转α°(0°<α<180°) .
(1)如图2,若α=26°,则∠BOP= ,∠AOM+∠BOQ= .
(2)若射线OC是∠BOM的角平分线,且∠POC=β°
①若△AOB旋转到图3的位置,∠BON的度数为多少?(用含β的代数式表示)
②△AOB在旋转过程中,若∠AOC=2∠AOM,求此时β的值.
答案解析部分
1.【答案】A
2.【答案】C
3.【答案】D
4.【答案】B
5.【答案】A
6.【答案】A
7.【答案】D
8.【答案】B
9.【答案】11.45
10.【答案】59.4
11.【答案】35
12.【答案】<
13.【答案】①③
14.【答案】互余
15.【答案】两点之间,线段最短
16.【答案】28;12
17.【答案】解:如图
18.【答案】解:如图:
∵∠AOC=70°,
∴∠BOC=180°-70°=110°,
∵EO⊥CD,
∴∠BOE=∠BOC-∠COE=20°;
如图,
∵∠AOC=70°,
∴∠BOD=70°,
∵EO⊥CD,
∴∠BOE=∠BOD+∠DOE=160°;
综上:∠BOE的度数为20°或160°.
19.【答案】解:∠BOC=∠AOB-∠AOC
=90°-50°
=40°,
∵ OB平分 ,
∴∠COD=2∠BOC=80°,
∴∠DOE=180°-∠COD=100°.
20.【答案】解:由题意,得PA= 40×15= 600(m),PB=40× 20= 800(m),
AB=1 000 m.
∵PA2+ PB2 = 6002+ 8002=1 0002=AB2,
∴△APB为直角三角形,∠APB= 90°.
∵∠NPA= =30° ,所以∠SPB= 60°,
∴乙客轮的航行方向为南偏东60°.
21.【答案】解:∠AOC=∠EDC.理由如下:
∵△ABC的三个内角的平分线交于点O,
∴∠OAC= ∠BAC,∠OCA= ∠ACB,∠OBC= ∠ABC.
∴∠AOC= 180°-(∠OAC+∠OCA)=180°- (∠BAC+∠BCA)=180°- (180°-∠ABC)=90°+ ∠ABC=90°+∠OBC.
∵DE⊥OB,所以∠BED= 90°.
∴∠EDC= 180°-∠EDB=∠OBC+∠BED= 90°+∠OBC.
∴∠AOC=∠EDC.
22.【答案】解:∵∠1=∠4,∠2=∠3(对顶角相等)
又∠1=∠2(已知)
所以∠3=∠4(等量代换)
∴a//b(内错角相等,两直线平行)
23.【答案】解:设 , , ,
,
平分 ,
,
,
,
解得: ,
, ,
.
24.【答案】证明:∵O是直线AB上一点
∴∠AOB=180°
∵∠COD与∠COE互余
∴∠COD+∠COE=90°
∴∠AOD+∠BOE=90°
∵OD是∠AOC的平分线
∴∠AOD=∠COD(理由:角平分线的定义)
∴∠BOE=∠COE(理由:等式性质)
∵∠AOE+∠BOE=180°
∴∠AOE+∠COE=180°
∴∠AOE与∠COE互补.
故答案为:90;COD; 角平分线的定义;等式性质,180.
25.【答案】(1)64°;180°
(2)①∵∠MOP=90°,∠POC=β°,
∴∠MOC=90°-β°,
∵OC是∠BOM的角平分线,
∴∠MOB=2∠MOC=180°-2β°,
∴∠BOP=90°-∠MOB=90°-(180°-2β°)=2β°-90°,
∵∠PON=90°,
∴∠BON=∠BOP+∠PON=2β°-90°+90°=2β°;
②如图,当OB旋转到OP的左侧时,
∵OC是∠BOM的角平分线,
∴∠COB=∠MOC,
∵∠AOC=2∠AOM,
∴∠AOM=∠MOC,
∴∠COB=∠MOC=∠AOM,
∵∠COB+∠MOC+∠AOM=90°,
∴∠COB=∠MOC=∠AOM=30°,
∴∠POC=β°=90°-∠MOC=90°-30°=60°,
②如图,当OB旋转到OP的右侧时,
设∠AOM=x,
∵∠AOC=2∠AOM=2x,
∴∠MOC=3∠AOM=3x,
∵∠COB+∠MOC+∠AOM=90°,
∴∠COB=∠MOC=∠AOM=30°,
∵OC是∠BOM的角平分线,
∴∠COB=∠MOC=3x,
∴∠AOB=∠AOC+∠BOC=5x=90°,
∴x=18°,
∴∠MOC=3x=54°,
∴∠POC=β°=90°-∠MOC=90°-54°=36°,
综上,β的值为60°或36°.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
