北师大版数学九年级上册 4.3 相似多边形 教学设计(表格式)
文档属性
| 名称 | 北师大版数学九年级上册 4.3 相似多边形 教学设计(表格式) |

|
|
| 格式 | docx | ||
| 文件大小 | 219.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-19 14:22:21 | ||
图片预览

文档简介
《4.3相似多边形》教学设计
课型 新授课 上课时间 第9周 主备人
项目 主备内容 二备内容
教学目标 1.了解相似多边形和相似比的概念; 2.会根据条件判断两个多边形是否为相似多边形; 3.掌握相似多边形的性质,并能根据相似比进行相关的计算.
教学重点 会根据相似多边形的定义判断两个多边形是否为相似多边形。
教学难点 掌握相似多边形的性质,并能根据相似比进行相关的计算.
教 学 过 程
实施步聚 主备内容 二备内容
内 容 教学方法
复习引入 连一连:在下列图形中找出形状相同的图形。 引导学生观察分析图形,从而准确地找出形状相同的图形。
新授一 知识点一:相似多边形的慨念和相似比的概念 一、请观察课本P86页图4-11,然后回答下列问题: 1.在这两个多边形中,是否有对应相等的内角 2.在这两个多边形中, 夹相等内角的两边是否成比例 二、尝试训练 1.(1)任意两个等边三角形相似吗?任意两个正方形呢?任意两个正n边形呢? (2)任意两个菱形相似吗? 2.(1)两个相似多边形一组对应边分别为3cm,4.5cm,那么它们的相似比为 .;(2)3如果多边形ABCDEF∽多边形A`B`C`D`E`F`,且∠A=68°,则∠A`等于 。 老师引导学生思考分析并计算。
新授二 知识点二:相似多边形的性质 相似多边形的性质:相似多边形的对应角相等,对应边成比例。 启发学生观察形状相同的图形有什么特征。
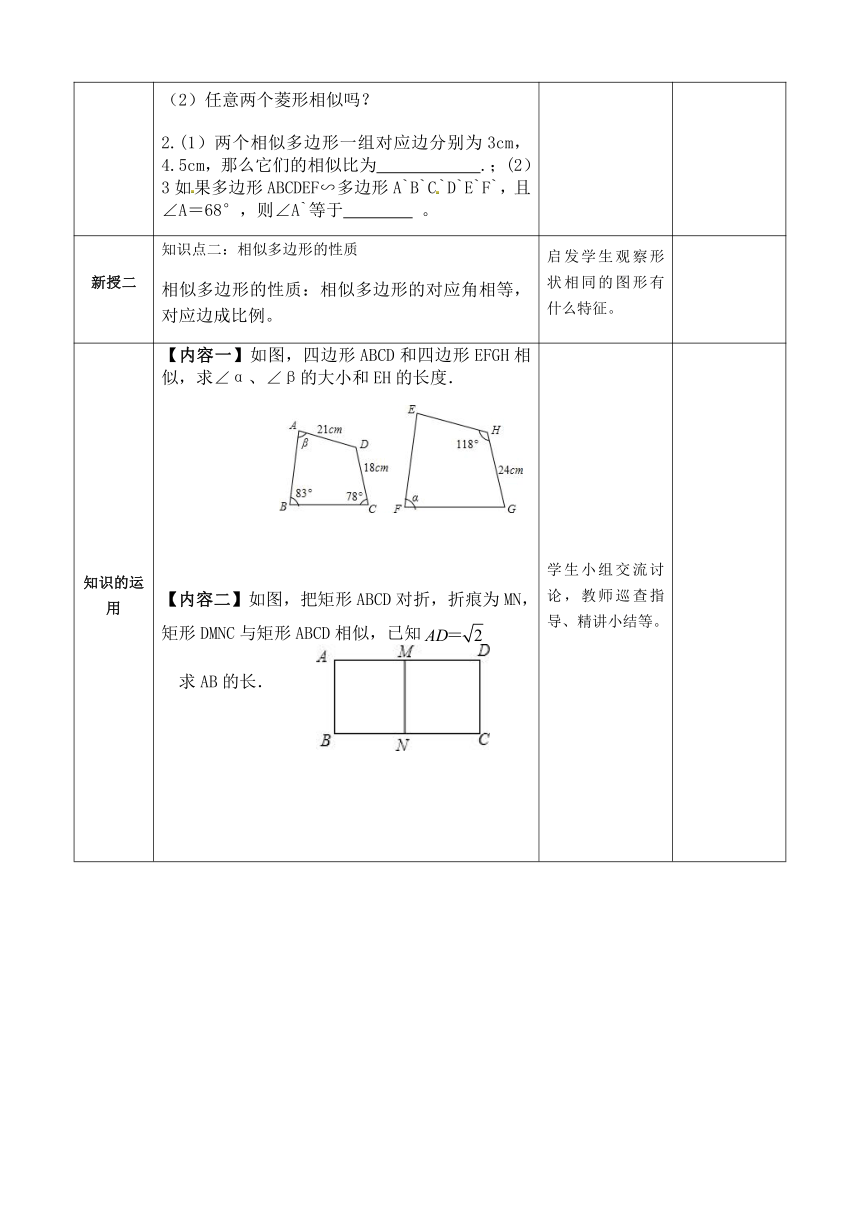
知识的运用 【内容一】如图,四边形ABCD和四边形EFGH相似,求∠α、∠β的大小和EH的长度. 【内容二】如图,把矩形ABCD对折,折痕为MN,矩形DMNC与矩形ABCD相似,已知 求AB的长. 学生小组交流讨论,教师巡查指导、精讲小结等。
当堂训练 1.下列说法中,正确的是( ) A.两个菱形一定相似 B.两个正方形一定相似 C.两个矩形一定相D.两个等腰梯形一定相似 2.五边形ABCDE∽五边形A′B′C′D′E′,若对应边AB与A′B′的长分别为50厘米和40厘米,则五边形ABCDE与五边形A′B′C′D′E′的相似比是________. 3.一个多边形的边长为2,3,4,5,6,另一个和它相似的多边形的最长边为24,则这个多边形的最短边长为 . 4.若四边形ABCD∽四边形A′B′C′D′,∠A=72°,∠B=95°,∠C=135°,则四边形A′B′C′D′的四个内角中最小角的度数为________. 5.把一个长方形鸡舍(如图)划分成两个全等的长方形.若要使每一个小长方形与原长方形相似,问原长方形应满足什么条件? 学生动手练习,老师巡视引导归纳。 目的是让学生掌握相似多边形的判定方法及其性质的运用。
小结 本节课你学到了什么 学生个人展示,教师归纳
板书设计 复习找出形状相同图形; 新授知识 (1)相似多边形和相似比的概念;(2)相似多边形的性质; 3、授例;例1 例2 4、小结
作业布置 《同步精炼》p41--p42练习
教学反思
课型 新授课 上课时间 第9周 主备人
项目 主备内容 二备内容
教学目标 1.了解相似多边形和相似比的概念; 2.会根据条件判断两个多边形是否为相似多边形; 3.掌握相似多边形的性质,并能根据相似比进行相关的计算.
教学重点 会根据相似多边形的定义判断两个多边形是否为相似多边形。
教学难点 掌握相似多边形的性质,并能根据相似比进行相关的计算.
教 学 过 程
实施步聚 主备内容 二备内容
内 容 教学方法
复习引入 连一连:在下列图形中找出形状相同的图形。 引导学生观察分析图形,从而准确地找出形状相同的图形。
新授一 知识点一:相似多边形的慨念和相似比的概念 一、请观察课本P86页图4-11,然后回答下列问题: 1.在这两个多边形中,是否有对应相等的内角 2.在这两个多边形中, 夹相等内角的两边是否成比例 二、尝试训练 1.(1)任意两个等边三角形相似吗?任意两个正方形呢?任意两个正n边形呢? (2)任意两个菱形相似吗? 2.(1)两个相似多边形一组对应边分别为3cm,4.5cm,那么它们的相似比为 .;(2)3如果多边形ABCDEF∽多边形A`B`C`D`E`F`,且∠A=68°,则∠A`等于 。 老师引导学生思考分析并计算。
新授二 知识点二:相似多边形的性质 相似多边形的性质:相似多边形的对应角相等,对应边成比例。 启发学生观察形状相同的图形有什么特征。
知识的运用 【内容一】如图,四边形ABCD和四边形EFGH相似,求∠α、∠β的大小和EH的长度. 【内容二】如图,把矩形ABCD对折,折痕为MN,矩形DMNC与矩形ABCD相似,已知 求AB的长. 学生小组交流讨论,教师巡查指导、精讲小结等。
当堂训练 1.下列说法中,正确的是( ) A.两个菱形一定相似 B.两个正方形一定相似 C.两个矩形一定相D.两个等腰梯形一定相似 2.五边形ABCDE∽五边形A′B′C′D′E′,若对应边AB与A′B′的长分别为50厘米和40厘米,则五边形ABCDE与五边形A′B′C′D′E′的相似比是________. 3.一个多边形的边长为2,3,4,5,6,另一个和它相似的多边形的最长边为24,则这个多边形的最短边长为 . 4.若四边形ABCD∽四边形A′B′C′D′,∠A=72°,∠B=95°,∠C=135°,则四边形A′B′C′D′的四个内角中最小角的度数为________. 5.把一个长方形鸡舍(如图)划分成两个全等的长方形.若要使每一个小长方形与原长方形相似,问原长方形应满足什么条件? 学生动手练习,老师巡视引导归纳。 目的是让学生掌握相似多边形的判定方法及其性质的运用。
小结 本节课你学到了什么 学生个人展示,教师归纳
板书设计 复习找出形状相同图形; 新授知识 (1)相似多边形和相似比的概念;(2)相似多边形的性质; 3、授例;例1 例2 4、小结
作业布置 《同步精炼》p41--p42练习
教学反思
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
