沪教版(五四学制)数学八上 19.1 命题与证明 教案(表格式)
文档属性
| 名称 | 沪教版(五四学制)数学八上 19.1 命题与证明 教案(表格式) |
|
|
| 格式 | doc | ||
| 文件大小 | 55.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-19 16:12:50 | ||
图片预览


文档简介
教学目标 教学内容 命题与证明
个性化学习问题解决
教学重点、难点
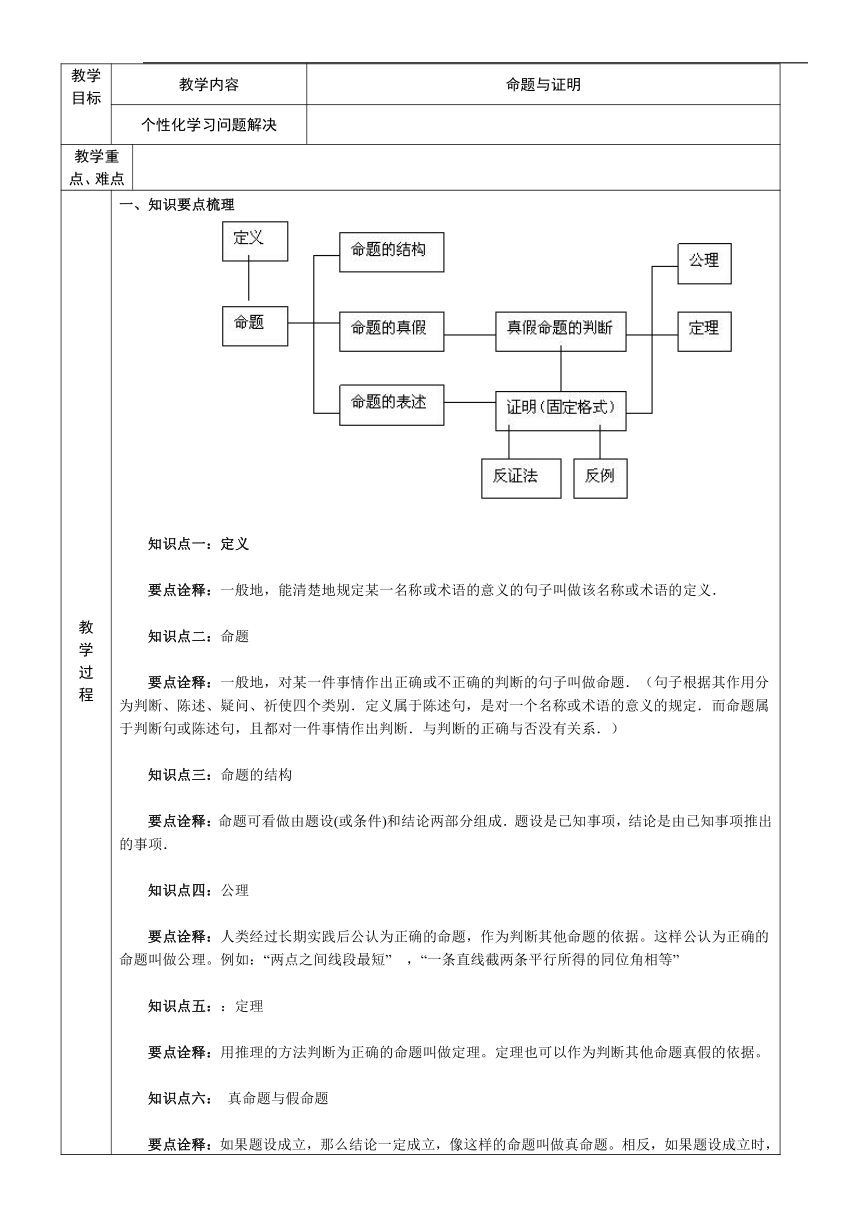
教学过程 一、知识要点梳理
知识点一:定义
要点诠释:一般地,能清楚地规定某一名称或术语的意义的句子叫做该名称或术语的定义.
知识点二:命题
要点诠释:一般地,对某一件事情作出正确或不正确的判断的句子叫做命题.(句子根据其作用分为判断、陈述、疑问、祈使四个类别.定义属于陈述句,是对一个名称或术语的意义的规定.而命题属于判断句或陈述句,且都对一件事情作出判断.与判断的正确与否没有关系.)
知识点三:命题的结构
要点诠释:命题可看做由题设(或条件)和结论两部分组成.题设是已知事项,结论是由已知事项推出的事项.
知识点四:公理
要点诠释:人类经过长期实践后公认为正确的命题,作为判断其他命题的依据。这样公认为正确的命题叫做公理。例如:“两点之间线段最短” ,“一条直线截两条平行所得的同位角相等”
知识点五::定理
要点诠释:用推理的方法判断为正确的命题叫做定理。定理也可以作为判断其他命题真假的依据。
知识点六: 真命题与假命题
要点诠释:如果题设成立,那么结论一定成立,像这样的命题叫做真命题。相反,如果题设成立时,不能保证结论总是正确的,就认为结论不成立,像这样的命题叫做假命题,凡是假命题都是错误的命题。
知识点七:证明
要点诠释:由题设出发,经过一步步的推理最后推出结论(书证)正确的过程叫做证明。证明中的每一步推理都要有根据,不能“想当然”,这些根据,可以是已知条件,也可以是定义、公理,在此以前学过的定理。(证明命题的格式一般为:1)按题意画出图形;2)分清命题的条件和结论,结合图形在“已知”中写出条件,在“求证”中写出结论;3)在“证明”中写出推理过程)
知识点八:假命题的判定
要点诠释:只需举出反例,它符合命题的题设,但不满足结论,即可判定该命题是假命题。
知识点九:反证法
要点诠释:从假设所需证的命题的结论不成立出发,结合条件推出与已知条件或正确命题相矛盾的结论,说明假设错误,原命题成立的证明方法
二、规律方法指导
1.数学中判定一个命题是真命题,要经过证明.要判断一个命题是假命题,只需举一个反例即可.
2.证明的意义:在几何中,除了公理以外,不管所论及的命题的结论是多么明显,都必须通过推理来证明.
3.反证法的适用范围
(1)已知条件很少或由已知条件能推得的结论很少; (2)命题的结论以否定形式出现时;
(3)命题的结论以“至多”、“至少”的形式出现时 (4)命题的结论以“唯一”的形式出现;
(5)命题的结论以“无限”的形式出现时; (6)关于存在性命题;
(7)某些定理的逆定理。
三、经典例题透析
类型一:
例、 判断下列语句在表述形式上,哪些对事情作了判断?哪些没有对事情作出判断?
(1)对顶角相等; (2)画一个角等于已知角; (3)两直线平行,同位角相等;
(4),两条直线平行吗 (5)鸟是动物; (6)若,求的值; (7)若,则.
思路点拨:通过本题熟悉命题的定义
总结升华:数学课的主要研究对象是数学知识,所以今后的相关学习是研究数学命题。
举一反三:
【变式1】下列语句中,哪些是命题,哪些不是命题
(1)若a<b,则;
(2)三角形的三条高交于一点;
(3)在ΔABC中,若AB>AC,则∠C>∠B吗
(4)两点之间线段最短;
(5)解方程;
(6)1+2≠3.
类型二:
例、指出下列命题的条件和结论,并改写成“如果……那么……”的形式:
(1)三条边对应相等的两个三角形全等;
(2)在同一个三角形中,等角对等边;
(3)对顶角相等;
(4)同角的余角相等;
(5)三角形的内角和等于180°;
(6)角平分线上的点到角的两边距离相等.
思路点拨: 找出命题的条件和结论是本题的难点,因为命题在叙述时要求通顺和简练,把命题中的有些词或句子省略了,在改写时注意要把省略的词或句子添加上去.
总结升华:注意原命题中省略的重要内内容一定要补充完整。
举一反三:
【变式1】试将下列各个命题的题设和结论相互颠倒或变为否定式,得到新的命题,并判断这些命题的真假.
(1)对顶角相等;
(2)两直线平行,同位角相等;
(3)若a=0,则ab=0;
(4)两条直线不平行,则一定相交;
【变式2】判断正误:
(1)如果两个角是对顶角,那么这两个角相等。 ( )
(2)如果两个角相等,那么这两个角是对顶角。 ( )
(3)如果两个角有公共顶点,那么这两个角是对顶角。 ( )
(4)如果两个角有公共顶点,有一条公共边,那么这两个角是邻补角。 ( )
(5)如果两个角是邻补角,那么这两个角一定互为补角。 ( )
(6)如果两个角的和是180°,那么这两个角是邻补角。 ( )
(7)对顶角的角平分线在同一条直线上。 ( )
(8)如果两个角有公共顶点,且角平分线互为反向延长线,那么这两个角是对顶角。
注:判断题如果是正确的命题需要加以说明或论证,找出依据,如果是错误的命题,只要举出一个反例即可。
类型三:
例、证明:“如果一条直线和两条平行线中的一条垂直,这条直线也和另一条垂直.”
思路点拨: 总结步骤:
1.审题:分清命题的“题设”和“结论”.
2.译题:结合图形中的字母及符号,写出已知,求证.
3.想题:用“执因索果”(综合法);用“执果索因”(分析法)寻找论证推理的逻辑思路.一般是把二者结合起来思考,效果较好,这也叫综合分析法.
4.证题:从已知出发,每一步过程要有根据(定义,公理或定理)最后得到结论,全面推理过程要因果分明.
解析:已知:a∥b,a⊥c,
求证:b⊥c
【变式1】求证:同角的余角相等.
已知:∠2是∠1的余角,∠3是∠1的余角.
求证:∠2=∠3.
类型四:
例、已知:如右图,直线l1,l2,l3在同一平面内,且l1∥l2,13与11相交于点P.
求证:13与l2相交.
(使用反证法)
思路点拨:仔细阅读反证法的定义,掌握这种方法的规律。
【变式1】用反证法证明不是有理数
【变式2】我们年级有367名学生,请你证明这些学生中至少有两个学生在同一天过生日.
个性化学习问题解决
教学重点、难点
教学过程 一、知识要点梳理
知识点一:定义
要点诠释:一般地,能清楚地规定某一名称或术语的意义的句子叫做该名称或术语的定义.
知识点二:命题
要点诠释:一般地,对某一件事情作出正确或不正确的判断的句子叫做命题.(句子根据其作用分为判断、陈述、疑问、祈使四个类别.定义属于陈述句,是对一个名称或术语的意义的规定.而命题属于判断句或陈述句,且都对一件事情作出判断.与判断的正确与否没有关系.)
知识点三:命题的结构
要点诠释:命题可看做由题设(或条件)和结论两部分组成.题设是已知事项,结论是由已知事项推出的事项.
知识点四:公理
要点诠释:人类经过长期实践后公认为正确的命题,作为判断其他命题的依据。这样公认为正确的命题叫做公理。例如:“两点之间线段最短” ,“一条直线截两条平行所得的同位角相等”
知识点五::定理
要点诠释:用推理的方法判断为正确的命题叫做定理。定理也可以作为判断其他命题真假的依据。
知识点六: 真命题与假命题
要点诠释:如果题设成立,那么结论一定成立,像这样的命题叫做真命题。相反,如果题设成立时,不能保证结论总是正确的,就认为结论不成立,像这样的命题叫做假命题,凡是假命题都是错误的命题。
知识点七:证明
要点诠释:由题设出发,经过一步步的推理最后推出结论(书证)正确的过程叫做证明。证明中的每一步推理都要有根据,不能“想当然”,这些根据,可以是已知条件,也可以是定义、公理,在此以前学过的定理。(证明命题的格式一般为:1)按题意画出图形;2)分清命题的条件和结论,结合图形在“已知”中写出条件,在“求证”中写出结论;3)在“证明”中写出推理过程)
知识点八:假命题的判定
要点诠释:只需举出反例,它符合命题的题设,但不满足结论,即可判定该命题是假命题。
知识点九:反证法
要点诠释:从假设所需证的命题的结论不成立出发,结合条件推出与已知条件或正确命题相矛盾的结论,说明假设错误,原命题成立的证明方法
二、规律方法指导
1.数学中判定一个命题是真命题,要经过证明.要判断一个命题是假命题,只需举一个反例即可.
2.证明的意义:在几何中,除了公理以外,不管所论及的命题的结论是多么明显,都必须通过推理来证明.
3.反证法的适用范围
(1)已知条件很少或由已知条件能推得的结论很少; (2)命题的结论以否定形式出现时;
(3)命题的结论以“至多”、“至少”的形式出现时 (4)命题的结论以“唯一”的形式出现;
(5)命题的结论以“无限”的形式出现时; (6)关于存在性命题;
(7)某些定理的逆定理。
三、经典例题透析
类型一:
例、 判断下列语句在表述形式上,哪些对事情作了判断?哪些没有对事情作出判断?
(1)对顶角相等; (2)画一个角等于已知角; (3)两直线平行,同位角相等;
(4),两条直线平行吗 (5)鸟是动物; (6)若,求的值; (7)若,则.
思路点拨:通过本题熟悉命题的定义
总结升华:数学课的主要研究对象是数学知识,所以今后的相关学习是研究数学命题。
举一反三:
【变式1】下列语句中,哪些是命题,哪些不是命题
(1)若a<b,则;
(2)三角形的三条高交于一点;
(3)在ΔABC中,若AB>AC,则∠C>∠B吗
(4)两点之间线段最短;
(5)解方程;
(6)1+2≠3.
类型二:
例、指出下列命题的条件和结论,并改写成“如果……那么……”的形式:
(1)三条边对应相等的两个三角形全等;
(2)在同一个三角形中,等角对等边;
(3)对顶角相等;
(4)同角的余角相等;
(5)三角形的内角和等于180°;
(6)角平分线上的点到角的两边距离相等.
思路点拨: 找出命题的条件和结论是本题的难点,因为命题在叙述时要求通顺和简练,把命题中的有些词或句子省略了,在改写时注意要把省略的词或句子添加上去.
总结升华:注意原命题中省略的重要内内容一定要补充完整。
举一反三:
【变式1】试将下列各个命题的题设和结论相互颠倒或变为否定式,得到新的命题,并判断这些命题的真假.
(1)对顶角相等;
(2)两直线平行,同位角相等;
(3)若a=0,则ab=0;
(4)两条直线不平行,则一定相交;
【变式2】判断正误:
(1)如果两个角是对顶角,那么这两个角相等。 ( )
(2)如果两个角相等,那么这两个角是对顶角。 ( )
(3)如果两个角有公共顶点,那么这两个角是对顶角。 ( )
(4)如果两个角有公共顶点,有一条公共边,那么这两个角是邻补角。 ( )
(5)如果两个角是邻补角,那么这两个角一定互为补角。 ( )
(6)如果两个角的和是180°,那么这两个角是邻补角。 ( )
(7)对顶角的角平分线在同一条直线上。 ( )
(8)如果两个角有公共顶点,且角平分线互为反向延长线,那么这两个角是对顶角。
注:判断题如果是正确的命题需要加以说明或论证,找出依据,如果是错误的命题,只要举出一个反例即可。
类型三:
例、证明:“如果一条直线和两条平行线中的一条垂直,这条直线也和另一条垂直.”
思路点拨: 总结步骤:
1.审题:分清命题的“题设”和“结论”.
2.译题:结合图形中的字母及符号,写出已知,求证.
3.想题:用“执因索果”(综合法);用“执果索因”(分析法)寻找论证推理的逻辑思路.一般是把二者结合起来思考,效果较好,这也叫综合分析法.
4.证题:从已知出发,每一步过程要有根据(定义,公理或定理)最后得到结论,全面推理过程要因果分明.
解析:已知:a∥b,a⊥c,
求证:b⊥c
【变式1】求证:同角的余角相等.
已知:∠2是∠1的余角,∠3是∠1的余角.
求证:∠2=∠3.
类型四:
例、已知:如右图,直线l1,l2,l3在同一平面内,且l1∥l2,13与11相交于点P.
求证:13与l2相交.
(使用反证法)
思路点拨:仔细阅读反证法的定义,掌握这种方法的规律。
【变式1】用反证法证明不是有理数
【变式2】我们年级有367名学生,请你证明这些学生中至少有两个学生在同一天过生日.
