沪教版(五四学制)数学八上 19.7 直角三角形全等的判定 教案(表格式)
文档属性
| 名称 | 沪教版(五四学制)数学八上 19.7 直角三角形全等的判定 教案(表格式) |
|
|
| 格式 | doc | ||
| 文件大小 | 131.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-19 16:12:58 | ||
图片预览

文档简介
19.7直角三角形全等的判定
【教学目标】
1. 通过探索判定两个直角三角形全等的特殊的方法,体会特殊与一般的关系,掌握“H.L”这一判定两个直角三角形全等的特殊方法.
2. 会利用“H.L”判定方法和一般三角形全等的方法判定直角三角形全等.
3. 在探索判定两个直角三角形全等的特殊的方法的过程中体验转化的思想.
【教学重难点】
重点: “斜边直角边”判定方法判定两个直角三角形全等的掌握和应用.
难点: 探索判定两个直角三角形全等的特殊的方法.
【教学过程】
教学过程 设计意图
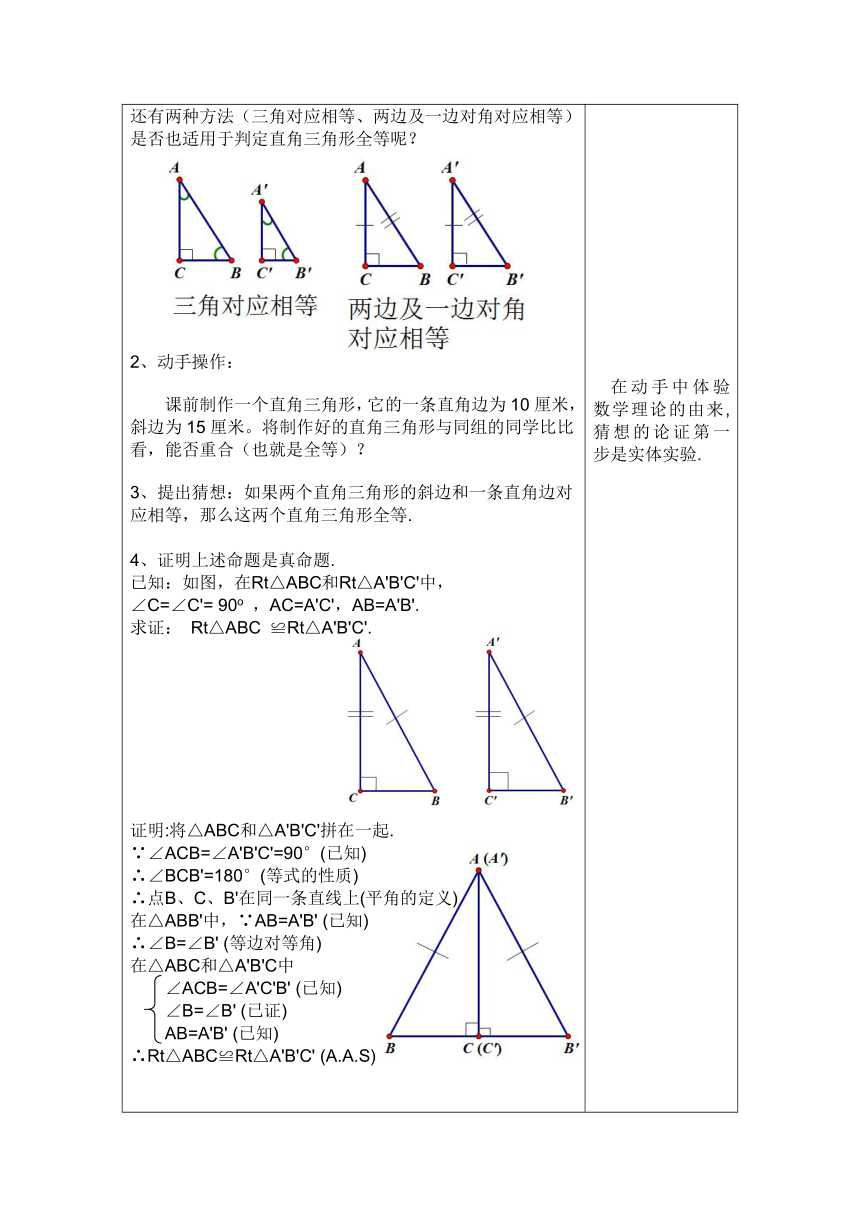
1、合作交流,探索新知:已知Rt△ABC和Rt△A'B'C',∠C=∠C'=90°,再添加两个条件,使Rt△ABC≌Rt△A'B'C',有哪些方法?如: 等.还有两种方法(三角对应相等、两边及一边对角对应相等)是否也适用于判定直角三角形全等呢? 2、动手操作:课前制作一个直角三角形,它的一条直角边为10厘米,斜边为15厘米。将制作好的直角三角形与同组的同学比比看,能否重合(也就是全等)?3、提出猜想:如果两个直角三角形的斜边和一条直角边对应相等,那么这两个直角三角形全等.4、证明上述命题是真命题.已知:如图,在Rt△ABC和Rt△A'B'C'中,∠C=∠C'= 90o ,AC=A'C',AB=A'B'.求证: Rt△ABC ≌Rt△A'B'C'.证明:将△ABC和△A'B'C'拼在一起.∵∠ACB=∠A'B'C'=90°(已知)∴∠BCB'=180°(等式的性质)∴点B、C、B'在同一条直线上(平角的定义) 在△ABB'中,∵AB=A'B' (已知)∴∠B=∠B' (等边对等角)在△ABC和△A'B'C中 ∠ACB=∠A'C'B' (已知) ∠B=∠B' (已证) AB=A'B' (已知) ∴Rt△ABC≌Rt△A'B'C' (A.A.S) 问题解决直角三角形全等的判定方法:如果两个直角三角形的斜边和一条直角边对应相等,那么这两个直角三角形全等.(简记为“H.L”)5、定理的应用例1.如图,BD⊥CD,CE⊥BE,且BD=CE.求证:BE=CD.分析:BE=CD 证明Rt△EBC≌Rt△DCB归纳:应用判定定理“HL”时,寻找“斜边和一条直角边对应相等”.并且“Rt”的符号不要漏写.变式:如图,△ABC中,BD⊥AC,CE⊥AB,BD=CE.求证:△ABC是等腰三角形. 分析:△ABC是等腰三角形 证明AB=AC 证明∠EBC=∠DCB 证明Rt△ADB≌Rt△ACE证明Rt△EBC≌Rt△DCB例题2 求证:在一个角的内部(包括顶点)且到角的两边距离相等的点,在这个角的平分线上. 已知:如图,QD⊥OA,QE⊥OB,垂足分别为D、E, QD= QE.求证:点Q在∠AOB的平分线上. 6、小结: (1)提问:你能够用几种方法证明两个直角三角形全等?直角三角形是特殊的三角形,所以不仅有一般三角形判定全等的方法: S.A.S、A.S.A、S.S.S、A.A.S,还有直角三角形特殊的判定方法——“HL”.(五种) (2)那么,H.L定理也适用于判定非直角三角形的全等吗 不适用.(特别的H.L给特别的直角三角形)7.思考题:已知:如图,EC⊥AB,FD⊥AB,垂足分别为C、D,AF=BE,FD=EC.求证:AC=BD.8、分层作业,发展个性 必做题:数学书P114 1、3题(抄题,画图,做题). 练习部分19.7 1、2、3题. 选做题:练习部分P70 第4题. 在此:强调直角三角形中已知了条件∠C=∠C,这是直角三角形的特殊之处.因此, S.A.S、A.S.A、S.S.S、A.A.S中有了一对角相等,还需要添加什么条件能证明两个三角形全等 (第一时间排除用SSS定理证明的情况) 改进定理的引入方法,使之符合学生的认知规律.在动手中体验数学理论的由来,猜想的论证第一步是实体实验.先引导学生分析题目,再出现过程。同时要加强规范学生的书写格式。直角三角形也有一般三角形的判定方法.温故知新,用新知识解决旧问题.体会化归的思想.
E
C
B
D
【教学目标】
1. 通过探索判定两个直角三角形全等的特殊的方法,体会特殊与一般的关系,掌握“H.L”这一判定两个直角三角形全等的特殊方法.
2. 会利用“H.L”判定方法和一般三角形全等的方法判定直角三角形全等.
3. 在探索判定两个直角三角形全等的特殊的方法的过程中体验转化的思想.
【教学重难点】
重点: “斜边直角边”判定方法判定两个直角三角形全等的掌握和应用.
难点: 探索判定两个直角三角形全等的特殊的方法.
【教学过程】
教学过程 设计意图
1、合作交流,探索新知:已知Rt△ABC和Rt△A'B'C',∠C=∠C'=90°,再添加两个条件,使Rt△ABC≌Rt△A'B'C',有哪些方法?如: 等.还有两种方法(三角对应相等、两边及一边对角对应相等)是否也适用于判定直角三角形全等呢? 2、动手操作:课前制作一个直角三角形,它的一条直角边为10厘米,斜边为15厘米。将制作好的直角三角形与同组的同学比比看,能否重合(也就是全等)?3、提出猜想:如果两个直角三角形的斜边和一条直角边对应相等,那么这两个直角三角形全等.4、证明上述命题是真命题.已知:如图,在Rt△ABC和Rt△A'B'C'中,∠C=∠C'= 90o ,AC=A'C',AB=A'B'.求证: Rt△ABC ≌Rt△A'B'C'.证明:将△ABC和△A'B'C'拼在一起.∵∠ACB=∠A'B'C'=90°(已知)∴∠BCB'=180°(等式的性质)∴点B、C、B'在同一条直线上(平角的定义) 在△ABB'中,∵AB=A'B' (已知)∴∠B=∠B' (等边对等角)在△ABC和△A'B'C中 ∠ACB=∠A'C'B' (已知) ∠B=∠B' (已证) AB=A'B' (已知) ∴Rt△ABC≌Rt△A'B'C' (A.A.S) 问题解决直角三角形全等的判定方法:如果两个直角三角形的斜边和一条直角边对应相等,那么这两个直角三角形全等.(简记为“H.L”)5、定理的应用例1.如图,BD⊥CD,CE⊥BE,且BD=CE.求证:BE=CD.分析:BE=CD 证明Rt△EBC≌Rt△DCB归纳:应用判定定理“HL”时,寻找“斜边和一条直角边对应相等”.并且“Rt”的符号不要漏写.变式:如图,△ABC中,BD⊥AC,CE⊥AB,BD=CE.求证:△ABC是等腰三角形. 分析:△ABC是等腰三角形 证明AB=AC 证明∠EBC=∠DCB 证明Rt△ADB≌Rt△ACE证明Rt△EBC≌Rt△DCB例题2 求证:在一个角的内部(包括顶点)且到角的两边距离相等的点,在这个角的平分线上. 已知:如图,QD⊥OA,QE⊥OB,垂足分别为D、E, QD= QE.求证:点Q在∠AOB的平分线上. 6、小结: (1)提问:你能够用几种方法证明两个直角三角形全等?直角三角形是特殊的三角形,所以不仅有一般三角形判定全等的方法: S.A.S、A.S.A、S.S.S、A.A.S,还有直角三角形特殊的判定方法——“HL”.(五种) (2)那么,H.L定理也适用于判定非直角三角形的全等吗 不适用.(特别的H.L给特别的直角三角形)7.思考题:已知:如图,EC⊥AB,FD⊥AB,垂足分别为C、D,AF=BE,FD=EC.求证:AC=BD.8、分层作业,发展个性 必做题:数学书P114 1、3题(抄题,画图,做题). 练习部分19.7 1、2、3题. 选做题:练习部分P70 第4题. 在此:强调直角三角形中已知了条件∠C=∠C,这是直角三角形的特殊之处.因此, S.A.S、A.S.A、S.S.S、A.A.S中有了一对角相等,还需要添加什么条件能证明两个三角形全等 (第一时间排除用SSS定理证明的情况) 改进定理的引入方法,使之符合学生的认知规律.在动手中体验数学理论的由来,猜想的论证第一步是实体实验.先引导学生分析题目,再出现过程。同时要加强规范学生的书写格式。直角三角形也有一般三角形的判定方法.温故知新,用新知识解决旧问题.体会化归的思想.
E
C
B
D
