2022-2023学年苏科版八年级数学上册第1章全等三角形 选择专项练习题 (word、含解析)
文档属性
| 名称 | 2022-2023学年苏科版八年级数学上册第1章全等三角形 选择专项练习题 (word、含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 374.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-20 16:07:26 | ||
图片预览


文档简介
2022-2023学年苏科版八年级数学上册《第1章全等三角形》选择专项练习题(附答案)
1.如图,若∠B=∠C,下列结论正确的是( )
A.△BOE≌△COD B.△ABD≌△ACE C.AE=AD D.∠AEC=∠ADB
2.如图,若△ABC≌△DEF,BD=22,AE=8,则BE等于( )
A.6 B.7 C.8 D.10
3.如图,已知∠DAB=∠CBA,添加下列条件不一定使△ABD与△BAC全等的是( )
A.BD=AC B.AD=BC C.∠D=∠C D.∠DBA=∠CAB
4.如图,已知AE=AC,∠C=∠E,若∠1=∠2可得△ABC≌△ADE,则判定这两个三角形全等的依据是( )
A.SSS B.ASA C.SAS D.AAS
5.如图,在△ABC中,∠B=80°,∠C=30°.若△ABC≌△ADE,∠DAC=32°,则∠EAC的度数为( )
A.18° B.30° C.32° D.38°
6.如图,在△ABC中,AD⊥BC于点D,CE⊥AB于点E,AD、CE交于点F,已知EF=EB=6,S△AEF=24,则CF的长为( )
A.1 B.2 C. D.3
7.如图,点E,F在AC上,AD=BC,DF=BE,下列条件中,能使△ADF≌△CBE的是( )
A.∠A=∠C B.AF=CE C.AD∥BC D.DF∥BE
8.如图,在Rt△ABC 中,∠ACB=90°,∠ABC=30° ,若△ABC≌△A′B′C ,且点A′ 恰好落在AB 上,则∠ACA′ 的度数为( )
A.30° B.45° C.50° D.60°
9.如图,为了测量B点到河对面的目标A之间的距离,在B点同侧选择一点C,测得∠ABC=75°,∠ACB=35°,然后在M处立了标杆,使∠MBC=75°,∠MCB=35°,得到△MBC≌△ABC,测得MB的长就是A,B两点间的距离,这里判定△MBC≌△ABC的理由是( )
A.SSS B.SAS C.ASA D.AAA
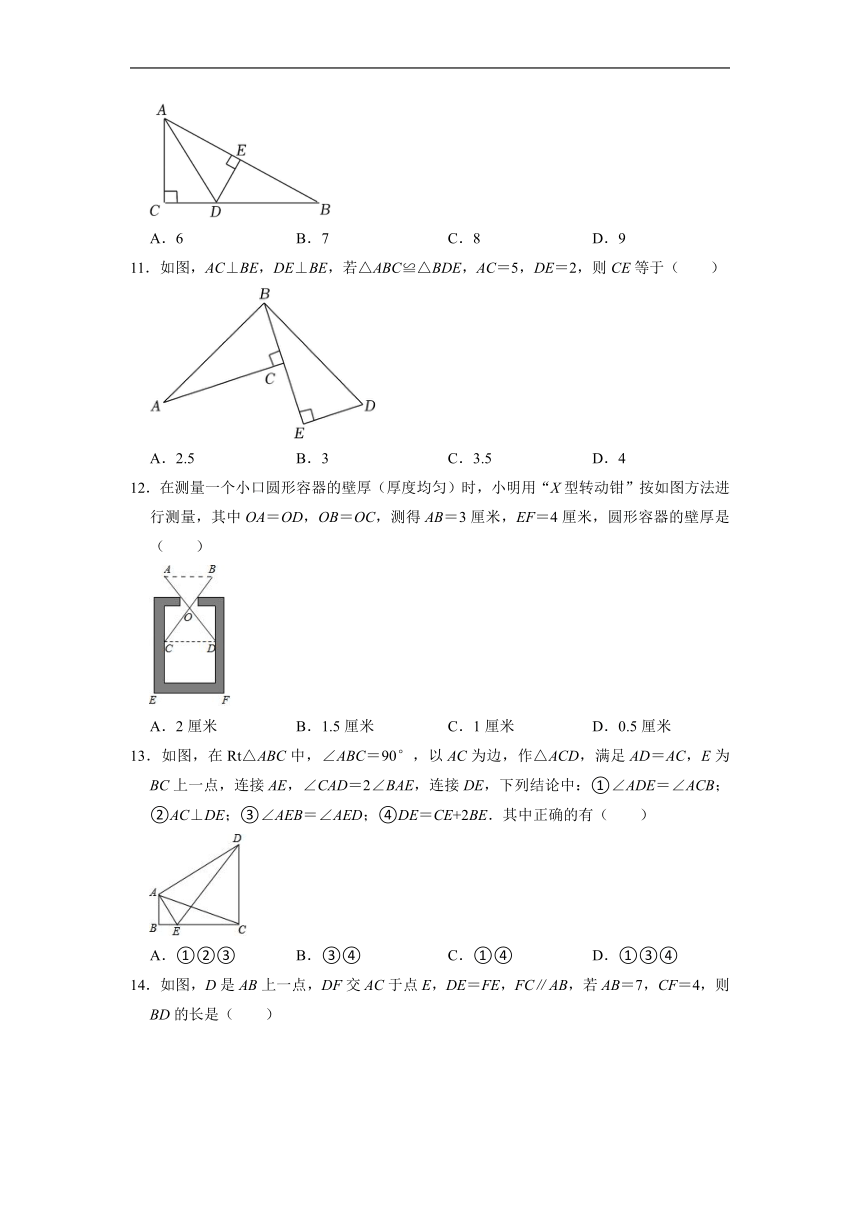
10.如图,在△ABC中,∠C=90°,D是BC上一点,DE⊥AB于点E,AE=AC,连接AD,若BC=8,则BD+DE等于( )
A.6 B.7 C.8 D.9
11.如图,AC⊥BE,DE⊥BE,若△ABC≌△BDE,AC=5,DE=2,则CE等于( )
A.2.5 B.3 C.3.5 D.4
12.在测量一个小口圆形容器的壁厚(厚度均匀)时,小明用“X型转动钳”按如图方法进行测量,其中OA=OD,OB=OC,测得AB=3厘米,EF=4厘米,圆形容器的壁厚是( )
A.2厘米 B.1.5厘米 C.1厘米 D.0.5厘米
13.如图,在Rt△ABC中,∠ABC=90°,以AC为边,作△ACD,满足AD=AC,E为BC上一点,连接AE,∠CAD=2∠BAE,连接DE,下列结论中:①∠ADE=∠ACB;②AC⊥DE;③∠AEB=∠AED;④DE=CE+2BE.其中正确的有( )
A.①②③ B.③④ C.①④ D.①③④
14.如图,D是AB上一点,DF交AC于点E,DE=FE,FC∥AB,若AB=7,CF=4,则BD的长是( )
A.5 B.4 C.3 D.2
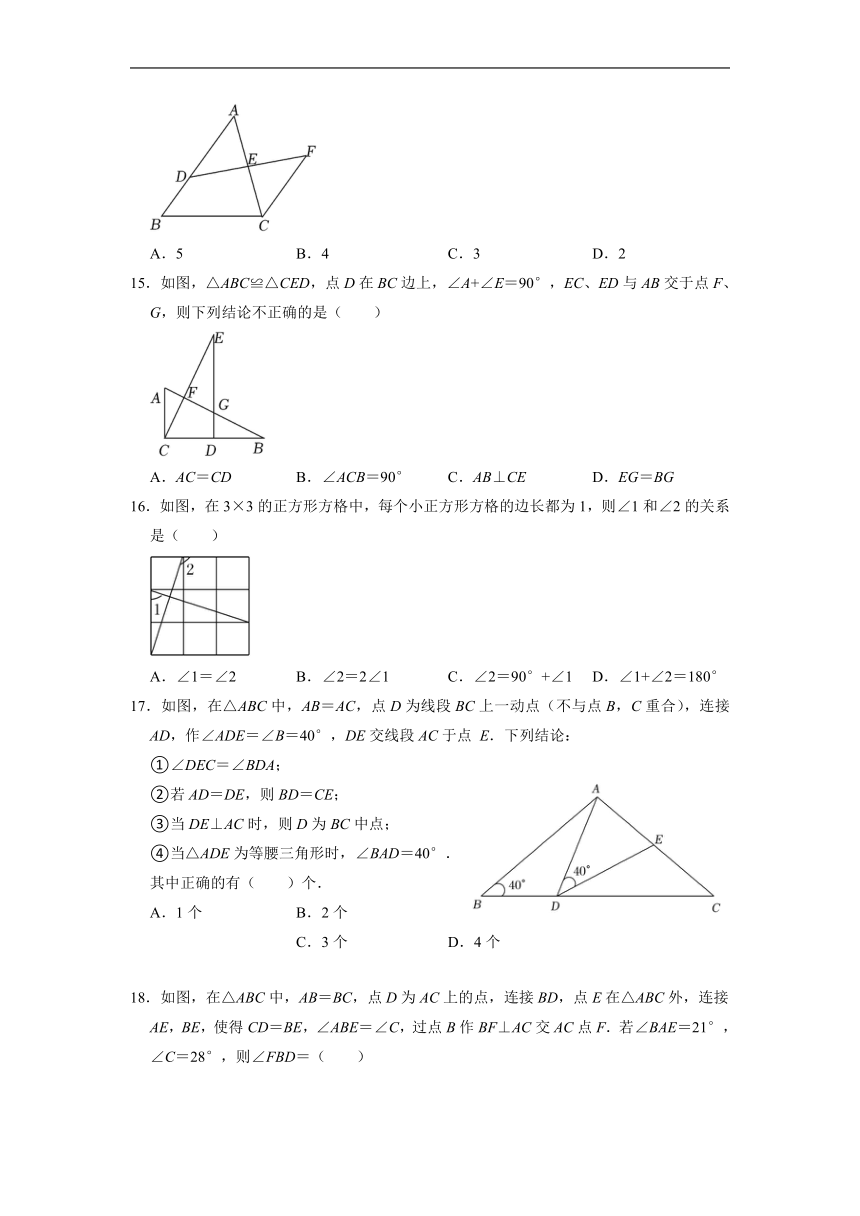
15.如图,△ABC≌△CED,点D在BC边上,∠A+∠E=90°,EC、ED与AB交于点F、G,则下列结论不正确的是( )
A.AC=CD B.∠ACB=90° C.AB⊥CE D.EG=BG
16.如图,在3×3的正方形方格中,每个小正方形方格的边长都为1,则∠1和∠2的关系是( )
A.∠1=∠2 B.∠2=2∠1 C.∠2=90°+∠1 D.∠1+∠2=180°
17.如图,在△ABC中,AB=AC,点D为线段BC上一动点(不与点B,C重合),连接AD,作∠ADE=∠B=40°,DE交线段AC于点 E.下列结论:
①∠DEC=∠BDA;
②若AD=DE,则BD=CE;
③当DE⊥AC时,则D为BC中点;
④当△ADE为等腰三角形时,∠BAD=40°.
其中正确的有( )个.
A.1个 B.2个 C.3个 D.4个
18.如图,在△ABC中,AB=BC,点D为AC上的点,连接BD,点E在△ABC外,连接AE,BE,使得CD=BE,∠ABE=∠C,过点B作BF⊥AC交AC点F.若∠BAE=21°,∠C=28°,则∠FBD=( )
A.49° B.59° C.41° D.51°
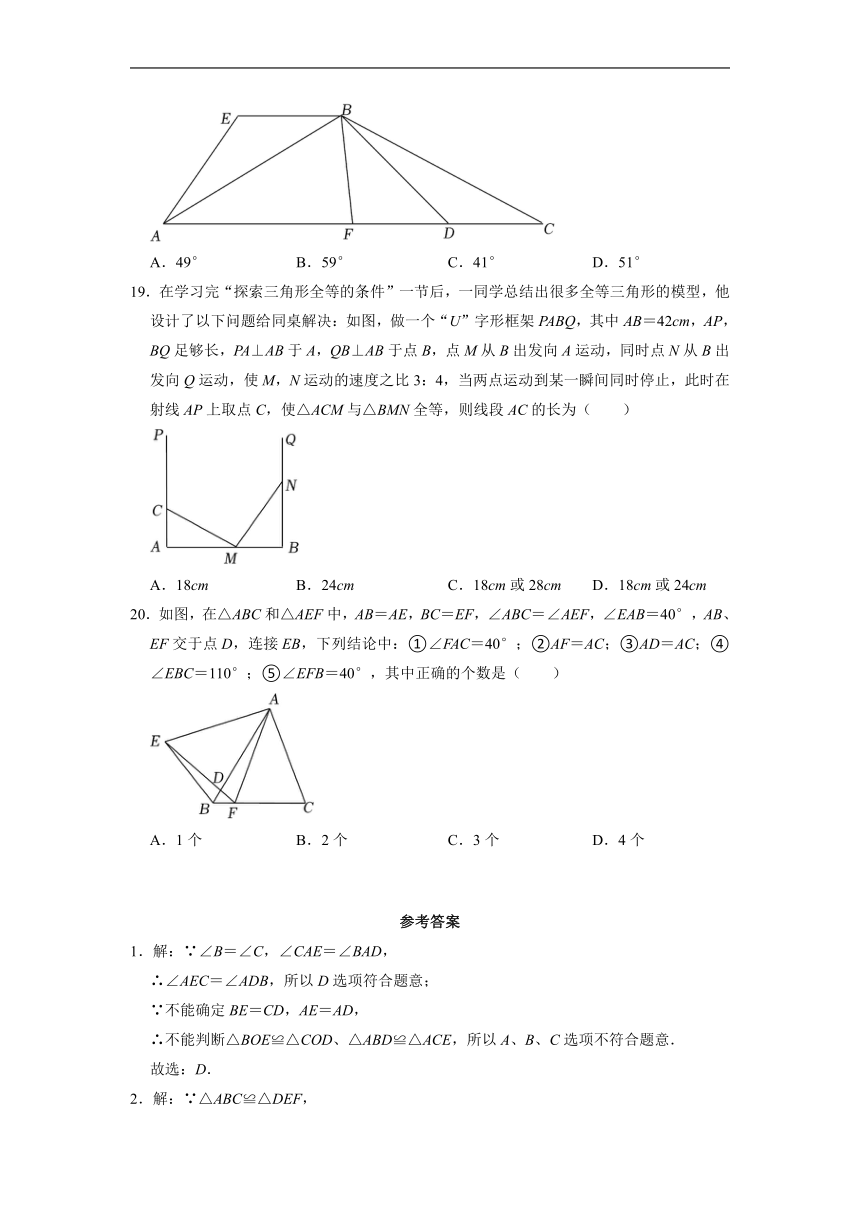
19.在学习完“探索三角形全等的条件”一节后,一同学总结出很多全等三角形的模型,他设计了以下问题给同桌解决:如图,做一个“U”字形框架PABQ,其中AB=42cm,AP,BQ足够长,PA⊥AB于A,QB⊥AB于点B,点M从B出发向A运动,同时点N从B出发向Q运动,使M,N运动的速度之比3:4,当两点运动到某一瞬间同时停止,此时在射线AP上取点C,使△ACM与△BMN全等,则线段AC的长为( )
A.18cm B.24cm C.18cm或28cm D.18cm或24cm
20.如图,在△ABC和△AEF中,AB=AE,BC=EF,∠ABC=∠AEF,∠EAB=40°,AB、EF交于点D,连接EB,下列结论中:①∠FAC=40°;②AF=AC;③AD=AC;④∠EBC=110°;⑤∠EFB=40°,其中正确的个数是( )
A.1个 B.2个 C.3个 D.4个
参考答案
1.解:∵∠B=∠C,∠CAE=∠BAD,
∴∠AEC=∠ADB,所以D选项符合题意;
∵不能确定BE=CD,AE=AD,
∴不能判断△BOE≌△COD、△ABD≌△ACE,所以A、B、C选项不符合题意.
故选:D.
2.解:∵△ABC≌△DEF,
∴AB=DE,
∵BD=22,AE=8,
∴BE=AD=(22﹣8)=7,
故选:B.
3.解:A.BD=AC,AB=BA,∠DAB=∠CBA,不符合全等三角形的判定定理,不能推出△ABD≌△BAC,故本选项符合题意;
B.AB=BA,∠DAB=∠CBA,AD=BC,符合全等三角形的判定定理SAS,能推出△ABD≌△BAC,故本选项不符合题意;
C.∠D=∠C,∠DAB=∠CBA,AB=BA,符合全等三角形的判定定理AAS,能推出△ABD≌△BAC,故本选项不符合题意;
D.∠DBA=∠CAB,AB=BA,∠DAB=∠CBA,符合全等三角形的判定定理ASA,能推出△ABD≌△BAC,故本选项不符合题意;
故选:A.
4.解:∵∠1=∠2,
∴∠1+∠DAC=∠2+∠DAC,
∴∠BAC=∠DAE,
∵AE=AC,∠C=∠E,
∴△ABC≌△ADE(ASA),
故选:B.
5.解:∵∠B=80°,∠C=30°,
∴∠BAC=70°,
∵∠DAC=32°,
∴∠BAD=38°,
∵△ABC≌△ADE,
∴∠BAC=∠DAE,
∴∠EAC=∠BAD=38°,
故选:D.
6.解:∵CE⊥AB,
∴∠AEC=90°,
∴S△AEF=×AE×EF=3AE=24,
∴AE=8,
∵AD⊥BC,
∴∠ADC=90°,
又∵∠AFE=∠CFD,
∴∠EAF=∠ECB,
∴△BEC≌△FEA(AAS),
∴AE=CE=8,
∴CF=CE﹣EF=8﹣6=2,
故选:B.
7.解:A、∵AD=BC,DF=BE,∠A=∠C,
∴△ADF与△CBE不一定全等,
故A不符合题意;
B、∵AD=BC,DF=BE,AF=CE,
∴△ADF≌△CBE(SSS),
故B符合题意;
C、∵AD∥BC,
∴∠A=∠C,
∵AD=BC,DF=BE,
∴△ADF与△CBE不一定全等,
故C不符合题意;
D、∵DF∥EB,
∴∠DFA=∠BEC,
∵AD=BC,DF=BE,
∴△ADF与△CBE不一定全等,
故D不符合题意;
故选:B.
8.解:∵∠ACB=90°,∠ABC=3 0°,
∴∠A=90°﹣30°=60° ,
∵△ABC≌△A′B′C ,
∴CA′=CA,
∴△ACA′ 为等边三角形,
∴∠ACA′=60° ,
故选:D.
9.解:在△MBC和△ABC中,
,
∴△MBC≌△ABC(ASA),
∴判定△MBC≌△ABC的理由是ASA,
故选:C.
10.解:∵DE⊥AB,
∴∠DEB=90°,
在Rt△ACD和Rt△AED中,
,
∴Rt△ACD≌Rt△AED(HL),
∴CD=DE,
∴BD+DE=BD+CD=BC,
∵BC=8,
∴BD+DE=BC=8.
故选:C.
11.解:∵△ABC≌△BDE,AC=5,DE=2,
∴BE=AC=5,BC=DE=2,
∴CE=BE﹣BC=5﹣2=3,
故选:B.
12.解:在△AOB和△DOC中,
,
∴△AOB≌△DOC(SAS),
∴AB=CD=3厘米,
∵EF=4厘米,
∴圆柱形容器的壁厚是×(4﹣3)=0.5(厘米),
故选:D.
13.解:如图,延长EB至G,使BE=BG,设AC与DE交于点M,
∵∠ABC=90°,
∴AB⊥GE,
∴AB垂直平分GE,
∴AG=AE,∠GAB=∠BAE=∠DAC,
∵∠BAE=∠GAE,
∴∠GAE=∠CAD,
∴∠GAE+∠EAC=∠CAD+∠EAC,
∴∠GAC=∠EAD,
在△GAC与△EAD中,
,
∴△GAC≌△EAD(SAS),
∴∠G=∠AED,∠ACB=∠ADE,故①是正确的;
∵AG=AE,
∴∠G=∠AEG=∠AED,故③正确;
∴AE平分∠BED,
当∠BAE=∠EAC时,∠AME=∠ABE=90°,则AC⊥DE,
当∠BAE≠∠EAC时,∠AME≠∠ABE,则无法说明AC⊥DE,故②是不正确的;
∵△GAC≌△EAD,
∴CG=DE,
∵CG=CE+GE=CE+2BE,
∴DE=CE+2BE,故④是正确的,
综上所述:其中正确的有①③④.
故选:D.
14.解:∵CF∥AB,
∴∠A=∠FCE,∠ADE=∠F,
在△ADE和△FCE中,
,
∴△ADE≌△CFE(AAS),
∴AD=CF=4,
∵AB=7,
∴DB=AB﹣AD=7﹣4=3.
故选:C.
15.解:∵△ABC≌△CED,
∴AC=CD,
故A选项不符合题意;
∵△ABC≌△CED,
∴∠B=∠E,
∵∠A+∠E=90°,
∴∠A+∠B=90°,
∴∠ACB=90°,
故B选项不符合题意;
∵△ABC≌△CED,
∴∠CDE=∠ACB=90°,
∴∠BDG=90°,
∵∠B=∠E,∠BGD=∠EGF,
∴∠EFG=∠BDG=90°,
∴AB⊥CE,
故C选项不符合题意,
没有足够的条件证明EG=BG,
故D选项符合题意,
故选:D.
16.解:如图,
在△ABC与△EDF中,
,
∴△ABC≌△EDF(SAS),
∴∠1=∠ABC.
∵∠ABC+∠2=180°,
∴∠1+∠2=180°.
故选:D.
17.解:①∵∠ADC=∠B+∠BAD,∠B=∠ADE=40°,
∴∠BAD=∠CDE.
∵AB=AC,
∴∠B=∠C.
∴由三角形内角和定理知:∠DEC=∠BDA.
故①正确;
②∵AB=AC,
∴∠B=∠C=40°,
由①知:∠DEC=∠BDA.
∵AD=DE.
∴△ABD≌△DCE.
∴BD=CE,
故②正确;
③∵D为BC中点,AB=AC,
∴AD⊥BC,
∴∠ADC=90°,
∴∠CDE=50°,
∵∠C=40°,
∴∠DEC=90°,
∴DE⊥AC,
故③正确;
④∵∠C=40°,
∴∠AED>40°,
∴∠ADE≠∠AED,
∵△ADE为等腰三角形,
∴AE=DE或AD=DE,
当AE=DE时,∠DAE=∠ADE=40°,
∵∠BAC=180°﹣40°﹣40°=100°,
∴∠BAD=60°,
故④不正确.
故选:C.
18.解:在△ABE和△BCD中,
,
∴△ABE≌△BCD(SAS),
∴∠BAE=∠CBD,
∵∠BAE=21°,∠C=28°,
∴∠CBD=21°,
∴∠BDF=∠CBD+∠C=21°+28°=49°,
∵BF⊥AC,
∴∠BFD=90°,
∴∠FBD=90°﹣∠BDF=90°﹣49°=41°.
故选:C.
19.解:设:BM=3xcm,则BN=4xcm,
∵∠A=∠B=90°,
(1),当△ACM≌△BNM时,有BM=AM,BN=AC,
又AM+BM=42cm,
∴3x+3x=42,
∴x=7.
∴AC=BN=4x=28cm;
当△ACM≌△BMN时,有AM=BN,BM=AC,
又AM+BM=42cm,
∴4x+3x=42,
∴x=6,
∴AC=BM=18cm;
故选:C.
20.解:在△AEF和△ABC中,
∵EA=BA,∠AEF=∠ABC,EF=BC,
∴△AEF≌△ABC(SAS),
∴∠EAF=∠BAC,AF=AC,故②正确;
∴∠EAB=∠FAC=40°,故①正确;
∴∠C=∠AFC=∠AFE=70°,
∴∠EFB=180°﹣70°﹣70°=40°,故⑤正确;
∵AE=AB,∠EAB=40°,
∴∠AEB=∠ABE=70°,
若∠EBC=110°,则
∠ABC=40°=∠EAB,
∴∠EAB=∠ABC,
∴AE∥BC,显然与题目条件不符,故④错误;
若AD=AC,则∠ADF=∠AFD=70°,
∴∠DAF=40°,这个显然与条件不符,故③错误.
故选:C.
1.如图,若∠B=∠C,下列结论正确的是( )
A.△BOE≌△COD B.△ABD≌△ACE C.AE=AD D.∠AEC=∠ADB
2.如图,若△ABC≌△DEF,BD=22,AE=8,则BE等于( )
A.6 B.7 C.8 D.10
3.如图,已知∠DAB=∠CBA,添加下列条件不一定使△ABD与△BAC全等的是( )
A.BD=AC B.AD=BC C.∠D=∠C D.∠DBA=∠CAB
4.如图,已知AE=AC,∠C=∠E,若∠1=∠2可得△ABC≌△ADE,则判定这两个三角形全等的依据是( )
A.SSS B.ASA C.SAS D.AAS
5.如图,在△ABC中,∠B=80°,∠C=30°.若△ABC≌△ADE,∠DAC=32°,则∠EAC的度数为( )
A.18° B.30° C.32° D.38°
6.如图,在△ABC中,AD⊥BC于点D,CE⊥AB于点E,AD、CE交于点F,已知EF=EB=6,S△AEF=24,则CF的长为( )
A.1 B.2 C. D.3
7.如图,点E,F在AC上,AD=BC,DF=BE,下列条件中,能使△ADF≌△CBE的是( )
A.∠A=∠C B.AF=CE C.AD∥BC D.DF∥BE
8.如图,在Rt△ABC 中,∠ACB=90°,∠ABC=30° ,若△ABC≌△A′B′C ,且点A′ 恰好落在AB 上,则∠ACA′ 的度数为( )
A.30° B.45° C.50° D.60°
9.如图,为了测量B点到河对面的目标A之间的距离,在B点同侧选择一点C,测得∠ABC=75°,∠ACB=35°,然后在M处立了标杆,使∠MBC=75°,∠MCB=35°,得到△MBC≌△ABC,测得MB的长就是A,B两点间的距离,这里判定△MBC≌△ABC的理由是( )
A.SSS B.SAS C.ASA D.AAA
10.如图,在△ABC中,∠C=90°,D是BC上一点,DE⊥AB于点E,AE=AC,连接AD,若BC=8,则BD+DE等于( )
A.6 B.7 C.8 D.9
11.如图,AC⊥BE,DE⊥BE,若△ABC≌△BDE,AC=5,DE=2,则CE等于( )
A.2.5 B.3 C.3.5 D.4
12.在测量一个小口圆形容器的壁厚(厚度均匀)时,小明用“X型转动钳”按如图方法进行测量,其中OA=OD,OB=OC,测得AB=3厘米,EF=4厘米,圆形容器的壁厚是( )
A.2厘米 B.1.5厘米 C.1厘米 D.0.5厘米
13.如图,在Rt△ABC中,∠ABC=90°,以AC为边,作△ACD,满足AD=AC,E为BC上一点,连接AE,∠CAD=2∠BAE,连接DE,下列结论中:①∠ADE=∠ACB;②AC⊥DE;③∠AEB=∠AED;④DE=CE+2BE.其中正确的有( )
A.①②③ B.③④ C.①④ D.①③④
14.如图,D是AB上一点,DF交AC于点E,DE=FE,FC∥AB,若AB=7,CF=4,则BD的长是( )
A.5 B.4 C.3 D.2
15.如图,△ABC≌△CED,点D在BC边上,∠A+∠E=90°,EC、ED与AB交于点F、G,则下列结论不正确的是( )
A.AC=CD B.∠ACB=90° C.AB⊥CE D.EG=BG
16.如图,在3×3的正方形方格中,每个小正方形方格的边长都为1,则∠1和∠2的关系是( )
A.∠1=∠2 B.∠2=2∠1 C.∠2=90°+∠1 D.∠1+∠2=180°
17.如图,在△ABC中,AB=AC,点D为线段BC上一动点(不与点B,C重合),连接AD,作∠ADE=∠B=40°,DE交线段AC于点 E.下列结论:
①∠DEC=∠BDA;
②若AD=DE,则BD=CE;
③当DE⊥AC时,则D为BC中点;
④当△ADE为等腰三角形时,∠BAD=40°.
其中正确的有( )个.
A.1个 B.2个 C.3个 D.4个
18.如图,在△ABC中,AB=BC,点D为AC上的点,连接BD,点E在△ABC外,连接AE,BE,使得CD=BE,∠ABE=∠C,过点B作BF⊥AC交AC点F.若∠BAE=21°,∠C=28°,则∠FBD=( )
A.49° B.59° C.41° D.51°
19.在学习完“探索三角形全等的条件”一节后,一同学总结出很多全等三角形的模型,他设计了以下问题给同桌解决:如图,做一个“U”字形框架PABQ,其中AB=42cm,AP,BQ足够长,PA⊥AB于A,QB⊥AB于点B,点M从B出发向A运动,同时点N从B出发向Q运动,使M,N运动的速度之比3:4,当两点运动到某一瞬间同时停止,此时在射线AP上取点C,使△ACM与△BMN全等,则线段AC的长为( )
A.18cm B.24cm C.18cm或28cm D.18cm或24cm
20.如图,在△ABC和△AEF中,AB=AE,BC=EF,∠ABC=∠AEF,∠EAB=40°,AB、EF交于点D,连接EB,下列结论中:①∠FAC=40°;②AF=AC;③AD=AC;④∠EBC=110°;⑤∠EFB=40°,其中正确的个数是( )
A.1个 B.2个 C.3个 D.4个
参考答案
1.解:∵∠B=∠C,∠CAE=∠BAD,
∴∠AEC=∠ADB,所以D选项符合题意;
∵不能确定BE=CD,AE=AD,
∴不能判断△BOE≌△COD、△ABD≌△ACE,所以A、B、C选项不符合题意.
故选:D.
2.解:∵△ABC≌△DEF,
∴AB=DE,
∵BD=22,AE=8,
∴BE=AD=(22﹣8)=7,
故选:B.
3.解:A.BD=AC,AB=BA,∠DAB=∠CBA,不符合全等三角形的判定定理,不能推出△ABD≌△BAC,故本选项符合题意;
B.AB=BA,∠DAB=∠CBA,AD=BC,符合全等三角形的判定定理SAS,能推出△ABD≌△BAC,故本选项不符合题意;
C.∠D=∠C,∠DAB=∠CBA,AB=BA,符合全等三角形的判定定理AAS,能推出△ABD≌△BAC,故本选项不符合题意;
D.∠DBA=∠CAB,AB=BA,∠DAB=∠CBA,符合全等三角形的判定定理ASA,能推出△ABD≌△BAC,故本选项不符合题意;
故选:A.
4.解:∵∠1=∠2,
∴∠1+∠DAC=∠2+∠DAC,
∴∠BAC=∠DAE,
∵AE=AC,∠C=∠E,
∴△ABC≌△ADE(ASA),
故选:B.
5.解:∵∠B=80°,∠C=30°,
∴∠BAC=70°,
∵∠DAC=32°,
∴∠BAD=38°,
∵△ABC≌△ADE,
∴∠BAC=∠DAE,
∴∠EAC=∠BAD=38°,
故选:D.
6.解:∵CE⊥AB,
∴∠AEC=90°,
∴S△AEF=×AE×EF=3AE=24,
∴AE=8,
∵AD⊥BC,
∴∠ADC=90°,
又∵∠AFE=∠CFD,
∴∠EAF=∠ECB,
∴△BEC≌△FEA(AAS),
∴AE=CE=8,
∴CF=CE﹣EF=8﹣6=2,
故选:B.
7.解:A、∵AD=BC,DF=BE,∠A=∠C,
∴△ADF与△CBE不一定全等,
故A不符合题意;
B、∵AD=BC,DF=BE,AF=CE,
∴△ADF≌△CBE(SSS),
故B符合题意;
C、∵AD∥BC,
∴∠A=∠C,
∵AD=BC,DF=BE,
∴△ADF与△CBE不一定全等,
故C不符合题意;
D、∵DF∥EB,
∴∠DFA=∠BEC,
∵AD=BC,DF=BE,
∴△ADF与△CBE不一定全等,
故D不符合题意;
故选:B.
8.解:∵∠ACB=90°,∠ABC=3 0°,
∴∠A=90°﹣30°=60° ,
∵△ABC≌△A′B′C ,
∴CA′=CA,
∴△ACA′ 为等边三角形,
∴∠ACA′=60° ,
故选:D.
9.解:在△MBC和△ABC中,
,
∴△MBC≌△ABC(ASA),
∴判定△MBC≌△ABC的理由是ASA,
故选:C.
10.解:∵DE⊥AB,
∴∠DEB=90°,
在Rt△ACD和Rt△AED中,
,
∴Rt△ACD≌Rt△AED(HL),
∴CD=DE,
∴BD+DE=BD+CD=BC,
∵BC=8,
∴BD+DE=BC=8.
故选:C.
11.解:∵△ABC≌△BDE,AC=5,DE=2,
∴BE=AC=5,BC=DE=2,
∴CE=BE﹣BC=5﹣2=3,
故选:B.
12.解:在△AOB和△DOC中,
,
∴△AOB≌△DOC(SAS),
∴AB=CD=3厘米,
∵EF=4厘米,
∴圆柱形容器的壁厚是×(4﹣3)=0.5(厘米),
故选:D.
13.解:如图,延长EB至G,使BE=BG,设AC与DE交于点M,
∵∠ABC=90°,
∴AB⊥GE,
∴AB垂直平分GE,
∴AG=AE,∠GAB=∠BAE=∠DAC,
∵∠BAE=∠GAE,
∴∠GAE=∠CAD,
∴∠GAE+∠EAC=∠CAD+∠EAC,
∴∠GAC=∠EAD,
在△GAC与△EAD中,
,
∴△GAC≌△EAD(SAS),
∴∠G=∠AED,∠ACB=∠ADE,故①是正确的;
∵AG=AE,
∴∠G=∠AEG=∠AED,故③正确;
∴AE平分∠BED,
当∠BAE=∠EAC时,∠AME=∠ABE=90°,则AC⊥DE,
当∠BAE≠∠EAC时,∠AME≠∠ABE,则无法说明AC⊥DE,故②是不正确的;
∵△GAC≌△EAD,
∴CG=DE,
∵CG=CE+GE=CE+2BE,
∴DE=CE+2BE,故④是正确的,
综上所述:其中正确的有①③④.
故选:D.
14.解:∵CF∥AB,
∴∠A=∠FCE,∠ADE=∠F,
在△ADE和△FCE中,
,
∴△ADE≌△CFE(AAS),
∴AD=CF=4,
∵AB=7,
∴DB=AB﹣AD=7﹣4=3.
故选:C.
15.解:∵△ABC≌△CED,
∴AC=CD,
故A选项不符合题意;
∵△ABC≌△CED,
∴∠B=∠E,
∵∠A+∠E=90°,
∴∠A+∠B=90°,
∴∠ACB=90°,
故B选项不符合题意;
∵△ABC≌△CED,
∴∠CDE=∠ACB=90°,
∴∠BDG=90°,
∵∠B=∠E,∠BGD=∠EGF,
∴∠EFG=∠BDG=90°,
∴AB⊥CE,
故C选项不符合题意,
没有足够的条件证明EG=BG,
故D选项符合题意,
故选:D.
16.解:如图,
在△ABC与△EDF中,
,
∴△ABC≌△EDF(SAS),
∴∠1=∠ABC.
∵∠ABC+∠2=180°,
∴∠1+∠2=180°.
故选:D.
17.解:①∵∠ADC=∠B+∠BAD,∠B=∠ADE=40°,
∴∠BAD=∠CDE.
∵AB=AC,
∴∠B=∠C.
∴由三角形内角和定理知:∠DEC=∠BDA.
故①正确;
②∵AB=AC,
∴∠B=∠C=40°,
由①知:∠DEC=∠BDA.
∵AD=DE.
∴△ABD≌△DCE.
∴BD=CE,
故②正确;
③∵D为BC中点,AB=AC,
∴AD⊥BC,
∴∠ADC=90°,
∴∠CDE=50°,
∵∠C=40°,
∴∠DEC=90°,
∴DE⊥AC,
故③正确;
④∵∠C=40°,
∴∠AED>40°,
∴∠ADE≠∠AED,
∵△ADE为等腰三角形,
∴AE=DE或AD=DE,
当AE=DE时,∠DAE=∠ADE=40°,
∵∠BAC=180°﹣40°﹣40°=100°,
∴∠BAD=60°,
故④不正确.
故选:C.
18.解:在△ABE和△BCD中,
,
∴△ABE≌△BCD(SAS),
∴∠BAE=∠CBD,
∵∠BAE=21°,∠C=28°,
∴∠CBD=21°,
∴∠BDF=∠CBD+∠C=21°+28°=49°,
∵BF⊥AC,
∴∠BFD=90°,
∴∠FBD=90°﹣∠BDF=90°﹣49°=41°.
故选:C.
19.解:设:BM=3xcm,则BN=4xcm,
∵∠A=∠B=90°,
(1),当△ACM≌△BNM时,有BM=AM,BN=AC,
又AM+BM=42cm,
∴3x+3x=42,
∴x=7.
∴AC=BN=4x=28cm;
当△ACM≌△BMN时,有AM=BN,BM=AC,
又AM+BM=42cm,
∴4x+3x=42,
∴x=6,
∴AC=BM=18cm;
故选:C.
20.解:在△AEF和△ABC中,
∵EA=BA,∠AEF=∠ABC,EF=BC,
∴△AEF≌△ABC(SAS),
∴∠EAF=∠BAC,AF=AC,故②正确;
∴∠EAB=∠FAC=40°,故①正确;
∴∠C=∠AFC=∠AFE=70°,
∴∠EFB=180°﹣70°﹣70°=40°,故⑤正确;
∵AE=AB,∠EAB=40°,
∴∠AEB=∠ABE=70°,
若∠EBC=110°,则
∠ABC=40°=∠EAB,
∴∠EAB=∠ABC,
∴AE∥BC,显然与题目条件不符,故④错误;
若AD=AC,则∠ADF=∠AFD=70°,
∴∠DAF=40°,这个显然与条件不符,故③错误.
故选:C.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
