2022—2023学年北师大版数学九年级上册2.6应用一元二次方程---九年级同步复习小测 (word、含解析)
文档属性
| 名称 | 2022—2023学年北师大版数学九年级上册2.6应用一元二次方程---九年级同步复习小测 (word、含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 132.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-20 16:53:32 | ||
图片预览




文档简介
2.6应用一元二次方程---九年级同步复习小测(基础复习+能力提升)
【北师大版】
【基础复习】
一、单选题
1.2018年第一季度,某企业营收入比2017年同期增长12%,2019年第一季度营收入比2018年同期增长10%,设2018年和2019年第一季度营收入的平均增长率为x,则可列方程( )
A.2x=12%+10%
B.(1+x)2=1+12%+10%
C.1+2x=(1+12%)(1+10%)
D.(1+x)2=(1+12%)(1+10%)
2.直角三角形两条直角边的和为7,面积是6,则斜边长是( )
A. B.5 C. D.7
3.某农场的粮食产量在两年内从2800吨增加到3090吨,若设平均每年增产的百分率为x,则所列的方程为( )
A.2800(1+2x)=3090 B.(1+x)2=290
C.2800(1+x)2=3090 D.2800(1+x2)=3090
4.用一条长40cm的绳子围成一个面积为64cm2的长方形.设长方形的长为xcm,则可列方程为( )
A.x(20+x)=64 B.x(20﹣x)=64
C.x(40+x)=64 D.x(40﹣x)=64
5.某地区计划举行校际篮球友谊赛,赛制为主客场形式(每两队之间在主客场各比赛一场),已知共比赛了30场次,则共有( )支队伍参赛.
A.4 B.5 C.6 D.7
6.近年来,全国房价不断上涨,某县2010年4月份的房价平均每平方米为3600元, 比2008年同期的房价平均每平方米上涨了2000元,假设这两年该县房价的平均增长率均为x,则关于x的方程为( )
A.(1+x)2=2000 B.2000(1+x)2=3600
C.(3600-2000)(1+x)=3600 D.(3600-2000)(1+x)2=3600
7.新冠病毒主要是经呼吸道飞沫传播的,在无防护下传播速度很快,已知有1个人患了新冠,经过两轮传染后共有625个人患了新冠,每轮传染中平均一个人传染m人,则m的值为( )
A.20 B.22 C.24 D.25
8.从正方形铁片上截取2cm宽的一个矩形,剩余矩形的面积为80cm2,则原正方形的面积为( )
A.100 cm2 B.121 cm2 C.144 cm2 D.169 cm2
二、填空题
9.若一个数的平方等于这个数的3倍,则这个数为 .
10.现要在一个长为40m,宽为26m的矩形花园中修建等宽的小道,剩余的地方种植花草.如图所示,要使种植花草的面积为864m2,那么小道的宽度应是 m.
11.在一次商品交易会上,参加交易会的每两家公司之间都要签订一份合同,会议结束后统计共签订了78份合同,若设有x家公司出席了这次交易会,则可列方程为: .
12.学校打算用长16m的篱笆围成一个长方形的生物园饲养小动物,生物园的一面靠墙(如图),面积是30m2,求生物园的长和宽.设生物园的宽(与墙相邻的一边)为xm,则列出的方程为 .
13.有长为30m的篱笆,如图所示,一面靠墙(墙足够长),围成中间隔有一道篱笆的长方形花圃,当花圃的面积是72m2时,则AB= .
14.已知两个连续正偶数的积为224,则这两个连续的正偶数是 .
15.一块矩形菜地的面积是120平方米,如果它的长减少2米,那么菜地就变成了正方形,则原矩形的长是 米.
16.用一条长40cm的绳子围成一个面积为64cm2的矩形.设矩形的一边长为xcm,则可列方程为 .
三、解答题
17.将一段铁丝围成面积为 的矩形,且它的长比宽多 ,求矩形的长.
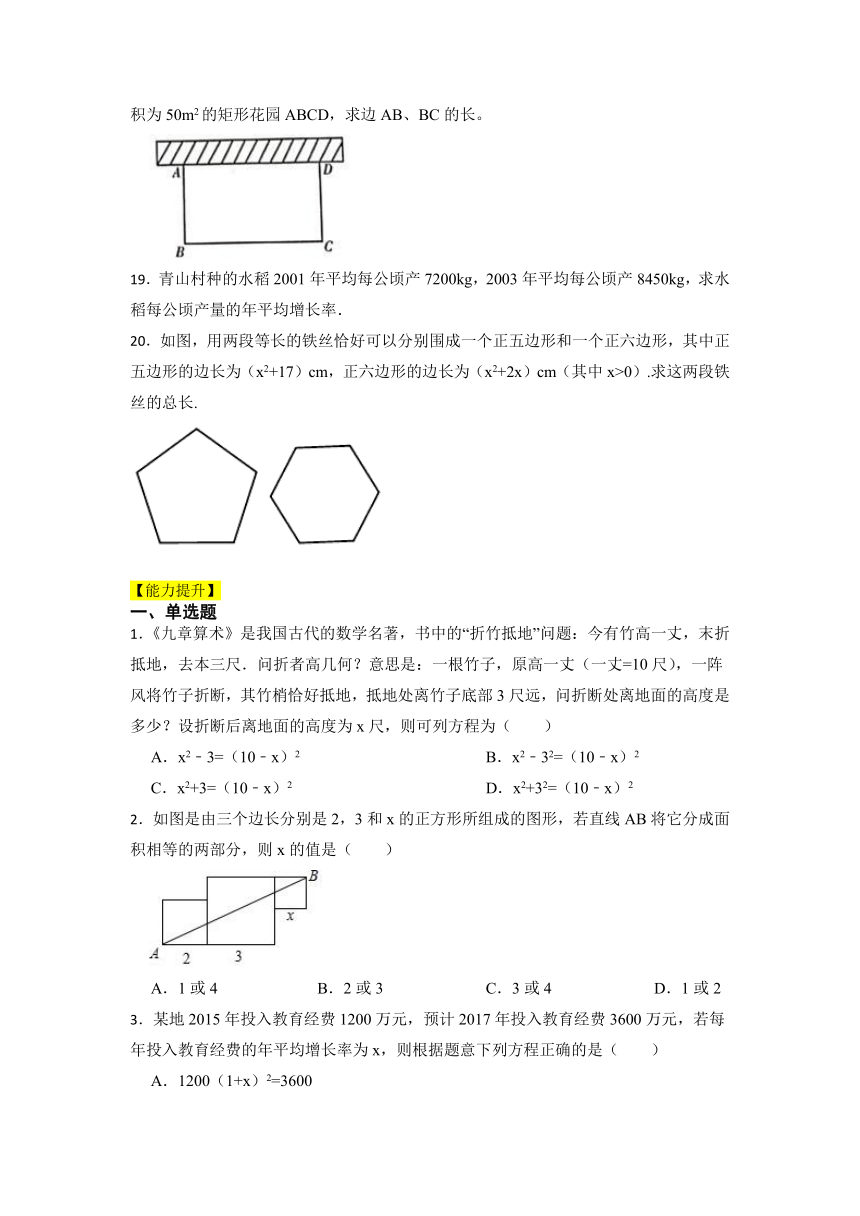
18.如图,某课外活动小组利用一面墙(墙足够长),另三边用20m长的篱笆围成一个面积为50m2的矩形花园ABCD,求边AB、BC的长。
19.青山村种的水稻2001年平均每公顷产7200kg,2003年平均每公顷产8450kg,求水稻每公顷产量的年平均增长率.
20.如图,用两段等长的铁丝恰好可以分别围成一个正五边形和一个正六边形,其中正五边形的边长为(x2+17)cm,正六边形的边长为(x2+2x)cm(其中x>0).求这两段铁丝的总长.
【能力提升】
一、单选题
1.《九章算术》是我国古代的数学名著,书中的“折竹抵地”问题:今有竹高一丈,末折抵地,去本三尺.问折者高几何?意思是:一根竹子,原高一丈(一丈=10尺),一阵风将竹子折断,其竹梢恰好抵地,抵地处离竹子底部3尺远,问折断处离地面的高度是多少?设折断后离地面的高度为x尺,则可列方程为( )
A.x2﹣3=(10﹣x)2 B.x2﹣32=(10﹣x)2
C.x2+3=(10﹣x)2 D.x2+32=(10﹣x)2
2.如图是由三个边长分别是2,3和x的正方形所组成的图形,若直线AB将它分成面积相等的两部分,则x的值是( )
A.1或4 B.2或3 C.3或4 D.1或2
3.某地2015年投入教育经费1200万元,预计2017年投入教育经费3600万元,若每年投入教育经费的年平均增长率为x,则根据题意下列方程正确的是( )
A.1200(1+x)2=3600
B.1200+1200(1+x)+1200(1+x)2=3600
C.1200(1﹣x)2=3600
D.1200(1+x)+1200(1+x)2=3600
4.某中学有一块长30m,宽20m的矩形空地,该中学计划在这块空地。上划出三分之二的区域种花,设计方案如图所示,求花带的宽度。设花带的宽度为xm,则可列方程为( )
A.(30-x)(20-x)= ×20×30
B.(30-2x)(20-x)= ×20×30
C.30x+2×20x= ×20×30
D.(30-2x)(20-x)= ×20×30
5.2019年第一季度,安徽省某企业生产总值比2018年同期增长14%,2020年第一季度受新冠肺炎疫情影响,生产总值比2019年同期减少了9%,设2019年和2020年第一季度生产总值平均增长率为x,则可列方程为( )
A.2x=14%-9%
B.(1+x)2=1+14%-9%
C.(1+x)2=(1+14%)(1-9%)
D.1+2x=(1+14%)(1-9%)
二、填空题
6.一个两位数,它的数值等于它的个位上的数字的平方的3倍,它的十位数字比个位数字大2.若设个位数字为x,列出求该两位数的方程式为 .
7.庆“元旦”,市工会组织篮球比赛,赛制为单循环形式(每两队之间都赛一场),共进行了45场比赛,这次有 队参加比赛
8.根据题意列出方程:有一面积为54m2的长方形,将它的一边剪短5m,另一边剪短2m,恰好变成一个正方形,这个正方形的边长是多少?设正方形的边长为xm,请列出你求解的方程 .
9.一种植物的主干长出若干数目的支干,每个支干又长出同样数目的小分支,主干、支干和小分支的总数是57,每个支干长出 个小分支.
10.一个两位数,个位数字比十位数字大3,个位数的平方恰好等于这个两位数,这个两位数是 .
三、解答题
11.如图所示,学校准备在教学楼后面搭建一简易矩形自行车车棚,一边利用教学楼的后墙(可利用的墙长为 ),另外三边利用学校现有总长 的铁栏围成,留出2米长门供学生进出.若围成的面积为 ,试求出自行车车棚的长和宽.
12.某商场今年二月份的营业额为400万元,三月份由于经营不善,其营业额比二月份下降10%.后来通过加强管理,五月份的营业额达到518.4万元.求三月份到五月份营业额的月平均增长率.
13.如图,某农场有一块长40m, 宽32m的矩形种植地,为方便管理,准备沿平行于两边的方向纵、横各修建一条等宽的小路,要使种植面积为1140m2, 求小路的宽
14.小知识:古希腊的毕达哥拉斯,在2500年前曾经大胆断言,一条线段(AB)的某一短线段(比如AC)与另一长线段(比如BC)之比,如果正好等于另一长线段(比如BC)同整个线段(AB)的比(即 ),那么这样的比例会给人一种美感,后来我们将分割这条线段(AB)的点C称为线段AB的“黄金分割点”.
在主持节目时,主持人站在舞台的黄金分割点处最自然得体,那么在长20米的舞台AB上,主持人从A点到B点走多少米,他的站台最得体?(取 =1.4, =1.7, =2.2)
15.某小区在绿化工程中有一块长为 ,宽为 的矩形空地,计划在其中修建两块相同的矩形绿地,使它们的面积之和为 ,两块绿地之间及周边留有宽度相等的人行通道(如图所示),求人行通道的宽度.
16.在一次酒会上,每两人都只碰一次杯,如果一共碰杯105次,则参加酒会的人数有多少人.
【基础复习答案】
1.【答案】D
【解析】【解答】解:设2018年和2019年第一季度营收入的平均增长率为x,
则可列方程(1+x)2=(1+12%)(1+10%),
故答案为:D.
【分析】设2018年和2019年第一季度营收入的平均增长率为x,再根据企业营收入比2017年同期增长12%,2019年第一季度营收入比2018年同期增长10%,列出方程即可解答
2.【答案】B
【解析】【解答】解:设其中一条直角边的长为x,则另一条直角边的长为(7﹣x),由题意,得
x(7﹣x)=6,
解得:x1=3.,x2=4,
由勾股定理,得
斜边为: =5.
故答案为:B.
【分析】根据直角三角形的面积求出量直角边的长,进而根据勾股定理得出答案。
3.【答案】C
【解析】【解答】从2800吨增加到3090吨,增长年数为2,增长率为x,则方程为:
2800(1+x)2=3090.
故选C.
【分析】本题考查了由实际问题抽象出一元二次方程中的增长率问题.关键是明确增长的基数,增长次数,增长后的值.
4.【答案】B
【解析】【解答】设长方形的长为xcm,则长方形的宽为(20-x)cm,
根据长方形的面积等于长乘以宽可列方程:x(20﹣x)=64,
故答案为:B.
【分析】根据长方形的面积=长×宽可列方程.
5.【答案】C
【解析】【解答】解:有x个球队参加比赛,
根据题意可列方程为:x(x1)=30,
解得:或(舍去);
∴共有6支队伍参赛;
故答案为:C
【分析】根据题意可设有x个球队参加比赛,由此列出方程解之即可。
6.【答案】D
【解析】【分析】2010年的房价为3600元,比2008年的上涨了2000元,即2008年房价为(3600-2000)元,而两年的平均增长率为x,则到了2010年的房价为(3600-2000)(1+x)2元,即3600元,由此可以列出方程式为:
(3600-2000)(1+x)2=3600
故选择D。
【点评】此类题目万变不离其宗,学生可以尝试多做此类题目,将会发现其中的规律。
7.【答案】C
【解析】【解答】由题意,第一轮会有 人被传染,
第二轮会有 人被传染,
则 ,
解得 或 (不符题意,舍去),
故答案为:C.
【分析】根据每轮传染中平均一个人传染m人,分别把第一轮和第二轮被传染的人分别表示出来,再根据两轮过后患者总数为625,列出方程求解即可.
8.【答案】A
【解析】【解答】解:设正方形边长为xcm,依题意得:
x2=2x+80,
解方程得x1=10,x2=﹣8(舍去),
所以正方形的面积是10×10=100(cm2),
故选:A.
【分析】从正方形铁片上截去2cm宽的一个长方形,所截去的长方形的长是正方形的边长,设边长是xcm,即可表示出截取的长方形的面积,根据剩余矩形的面积为80cm2,即正方形的面积=截去的长方形的面积+80cm2.即可列出方程求解.
9.【答案】3或0
【解析】【解答】设这个数是x, =3x
=3x
【分析】设这个数是x,根据一个数的平方等于这个数的3倍,列出方程,求解即可。
10.【答案】2
【解析】【解答】解:设小道的宽为x米,依题意得
(40-2x)(26-x)=864,
解之得
x1=44(舍去),x2=2.
故答案为:2.
【分析】设小道的宽为x米,利用平移的知识知: 种植花草的矩形的长和宽分别为(40-2x)、(26-x),再根据矩形的面积=矩形的长×宽可列关于x的方程,解方程可求解.
11.【答案】 x(x 1)=78
【解析】【解答】解:设有x家公司出席了这次交易会,依题意,得
x(x 1)=78.
故答案为: x(x 1)=78.
【分析】设有x家公司出席了这次交易会,由题意可知每个公司要签订(x-1)份合同,则共签订合同x(x-1)份,结合题意可列方程.
12.【答案】x(16-2x)=30
【解析】【解答】解:由题意得:生物园的长为
则由长方形的面积公式得:x(16-2x)=30
故答案为:x(16-2x)=30.
【分析】由题意得:生物园的长为(16-2x)m,然后利用矩形的面积公式进行解答.
13.【答案】4m或6m
【解析】【解答】解:设AB长为xm,则BC长为(30-3x)m,
根据题意得:x(30-3x)=72,
整理得:x2-10x+24=0,
解得:x1=4,x2=6.
答:AB的长4m或6m.
故答案是:4m或6m.
【分析】根据花圃的面积是72m2,可得x(30-3x)=72,再计算求解即可。
14.【答案】14,16
【解析】【解答】解:设较小的正偶数为x,则较大的正偶数为x+2,根据题意得
x(x+2)=224
解之:x1=14,x2=-16
∵x>0
∴x=14,
∴x+2=16.
故答案为:14,16.
【分析】设较小的正偶数为x,可表示出较大的正偶数,再根据两个连续正偶数的积为224,由此可得到关于x的方程,解方程求出x的值,然后求出这两个连续的正偶数.
15.【答案】12
【解析】【解答】解:∵长减少2m,菜地就变成正方形,
∴设原菜地的长为x米,则宽为(x﹣2)米,
根据题意得:x(x﹣2)=120,
解得:x=12或x=﹣10(舍去),
故答案为:12.
【分析】根据“如果它的长减少2m,那么菜地就变成正方形”可以得到长方形的长比宽多2米,利用矩形的面积公式列出方程即可.
16.【答案】x(20﹣x)=64
【解析】【解答】解:设矩形的一边长为xcm,
∵长方形的周长为40cm,
∴宽为=(20﹣x)(cm),
得x(20﹣x)=64.
故答案为:x(20﹣x)=64.
【分析】本题可根据长方形的周长可以用x表示宽的值,然后根据面积公式即可列出方程.
17.【答案】解:设矩形的长为 cm,则 解得: (不合题意,舍去),答:矩形的长为15cm.
【解析】【分析】实际中矩形的长不可能为负数,所以舍去 .
18.【答案】解:设边AB的长为xm. 根据题意,得 . 解得 . ∴AB=5,BC=20-2×5=10. ∴边AB的长为5m,边BC的长为10 m
【解析】【分析】 设边AB的长为xm ,根据等量关系,列出一元二次方程,即可求解.
19.【答案】解:设水稻每公顷产量的年平均增长率为x,
则有:7200(1+x)2=8450,
解得:x1= ≈0.0833,x2=﹣ =﹣2.0833(应舍去).
∴水稻每公顷产量的年平均增长率为8.33%
【解析】【分析】本题依据题中的等量关系水稻2001年平均每公顷产7200kg,2003年平均每公顷产8450kg,根据增长后的产量=增长前的产量(1+增长率),设增长率是x,则2003年的产量是7200(1+x)2据此即可列方程,解出后检验即可.
20.【答案】解:由已知得,正五边形周长为5(x2+17)cm,正六边形周长为6(x2+2x)cm,
∵正五边形和正六边形的周长相等,
∴5(x2+17)=6(x2+2x),
整理得x2+12x-85=0,配方得(x+6)2=121,
解得x1=5,x2=-17(舍去),
故正五边形的周长为5(52+17)=210(cm).
又因为两段铁丝等长,所以这两段铁丝的总长为420cm.
答:这两段铁丝的总长为420cm.
【解析】【分析】根据正五边形和正六边形的周长相等,列一元二次方程求x的值,得出正六边形的边长,再根据所求边长即可求两段铁丝的总长.
【能力提升答案】
1.【答案】D
【解析】【解答】解:设竹子折断处离地面x尺,则斜边为(10-x)尺,
根据勾股定理得:x2+32=(10-x)2.
故答案为:D
【分析】设竹子折断处离地面x尺,则斜边为(10-x)尺,根据勾股定理建立方程,即可。
2.【答案】D
【解析】【解答】解:如图,补全图形,
∵直线AB将它分成面积相等的两部分,
∴ (2+3+x)×3﹣x(3﹣x)= ×(2+3+x)×3﹣2×1,
解得x=1或x=2,
故答案为:D.
【分析】根据题意列出方程求解即可。
3.【答案】A
【解析】【解答】解: ∵年平均增长率为x,
∴两年后变为原来的 ,
∴可列方程1200(1+x)2=3600
故选A.
4.【答案】B
【解析】【解答】解: 设花带的宽度为xm,
根据题意得:(30-2x)(20-x)= ×20×30,
故答案为:B.
【分析】 设花带的宽度为xm,得出矩形空地的长为(30-2x)m,宽为(20-x)m,根据题意得出矩形空地的面积是原矩形面积的,列出方程即可求解.
5.【答案】C
【解析】【解答】∵2019年的生产总值为(1+14%),
∴2020年的生产总值为(1+14%)(1-9%),
得到方程为(1+x)2=(1+14%)(1-9%),
故答案为:C.
【分析】根据题意得到2019年的生产总值为(1+14%),2020年的生产总值为(1+14%)(1-9%),由此列方程即可.
6.【答案】10(x+2)+x=3x2
【解析】【解答】解:设个位数字为x,则这个数为3x2,十位数字为x+2,
由题意得,10(x+2)+x=3x2.
故答案为10(x+2)+x=3x2.
【分析】设个位数字为x,则这个数为3x2,十位数字为x+2,根据题意表示出这个两位数,列出方程.
7.【答案】10
【解析】【解答】解:设这次有x队参加比赛,则此次比赛的总场数为 场,
根据题意列出方程得: =45,
整理,得:x2-x-90=0,
解得:x1=10,x2=-9(不合题意舍去),
所以,这次有10队参加比赛.
【分析】设这次有x队参加比赛,由于赛制为单循环形式(每两队之间都赛一场),则此次比赛的总场数为 场.根据题意可知:此次比赛的总场数=45场,依此等量关系列出方程求解即可.
8.【答案】(x+5)(x+2)=54
【解析】【解答】解:设正方形的边长为xm,
那么长方形的两边应该为:x+5,x+2,
∴(x+5)(x+2)=54.
故答案为:(x+5)(x+2)=54.
【分析】如果设正方形的边长为xm,那么长方形的两边应该为:x+5,x+2,根据面积相等可列出的方程.
9.【答案】7
【解析】【解答】设每个支干长出x个小分支,
根据题意得: ,
解得: , (不符题意,舍去).
答:每个支干长出7个小分支.
答案是:7.
【分析】设每个支干长出x个小分支,根据主干、支干和小分支的总数是57,列出方程,即可求解.
10.【答案】25或36
【解析】【解答】解:设个位数字为x,那么十位数字是(x-3),这个两位数是10(x-3)+x,
依题意得:
∴
∴
∴x-3=2或3.
答:这个两位数是25或36.
故答案为:25或36.
【分析】设个位数字为x,那么十位数字是(x-3),这个两位数是[10(x-3)+x],然后根据个位数字的平方刚好等于这个两位数即可列出方程求解.
11.【答案】解: 现有总长 的铁栏围成,需留出2米长门
∴设 ,则 ;
根据题意列方程 ,
解得 , ;
当 , (米),
当 , (米),而墙长 ,不合题意舍去,
答:若围成的面积为 ,自行车车棚的长和宽分别为10米,18米.
【解析】【分析】设自行车车棚的宽AB为x米,则长为(38-2x)米,根据矩形的面积公式,即可列方程求解即可.
12.【答案】解:设三月份到五月份营业额的月平均增长率为x,
根据题意得,400×(1-10%)(1+x)2=518.4,
解得,x1=0.2=20%,x2=﹣2.2(不合题意,舍去).
答:三月份到五月份营业额的月平均增长率为20%.
【解析】【分析】设三月份到五月份营业额的月平均增长率为x,则四月份的营业额400×(1-10%)(1+x),五月份的营业额为400×(1-10%)(1+x)2,列出方程求解即可.
13.【答案】解:设小路的宽为xm,依题意有
(40-x)(32-x)=1140,
整理,得x2-72x+140=0.
解得x1=2,x2=70(不合题意,舍去).
答:小路的宽应是2m
【解析】【分析】设小路的宽为xm,采用平移法,可得出种植部分是边长为40-x和32-x的矩形,利用矩形的面积公式建立方程,解方程求出符合题意条件的x(0<x<32)的值。
14.【答案】解:设 ,则 ,
∴由题意得:当 即 ,
∴ ,
解得 , (舍去),
∴此时主持人从A点到B点走 ,
当 即 ,
∴ ,
解得 , (舍去),
∴此时主持人从A点到B点走 ,
∴综上所述,主持人从A点到B点走8m或12m时他的站台最得体.
答:主持人从A点到B点走8m或12m时他的站台最得体.
【解析】【分析】设AC=xm,则BC=(20-x)m,当BC2=AC·AB时,代入求解可得x,进而可得主持人从A点到B点走的距离;当AC2=BC·AB时,同理可得主持人从A点到B点走的距离,据此解答.
15.【答案】解:设人行道的宽度为 米,根据题意得
, (不合题意,舍去)
答:人行道的宽度是 .
【解析】【分析】设人行道的宽度为 米,根据题意列出方程求解即可。
16.【答案】解:设参加酒会的人数为x人,
依题意,得: x(x﹣1)=105,
整理,得:x2﹣x﹣210=0,
解得:x1=15,x2=﹣14(不合题意,舍去).
答:参加酒会的人数有15人
【解析】【分析】设参加酒会的人数为x人,根据每两人都只碰一次杯且一共碰杯105次,即可得出关于x的一元二次方程,解之取其正值即可得出结论.
【北师大版】
【基础复习】
一、单选题
1.2018年第一季度,某企业营收入比2017年同期增长12%,2019年第一季度营收入比2018年同期增长10%,设2018年和2019年第一季度营收入的平均增长率为x,则可列方程( )
A.2x=12%+10%
B.(1+x)2=1+12%+10%
C.1+2x=(1+12%)(1+10%)
D.(1+x)2=(1+12%)(1+10%)
2.直角三角形两条直角边的和为7,面积是6,则斜边长是( )
A. B.5 C. D.7
3.某农场的粮食产量在两年内从2800吨增加到3090吨,若设平均每年增产的百分率为x,则所列的方程为( )
A.2800(1+2x)=3090 B.(1+x)2=290
C.2800(1+x)2=3090 D.2800(1+x2)=3090
4.用一条长40cm的绳子围成一个面积为64cm2的长方形.设长方形的长为xcm,则可列方程为( )
A.x(20+x)=64 B.x(20﹣x)=64
C.x(40+x)=64 D.x(40﹣x)=64
5.某地区计划举行校际篮球友谊赛,赛制为主客场形式(每两队之间在主客场各比赛一场),已知共比赛了30场次,则共有( )支队伍参赛.
A.4 B.5 C.6 D.7
6.近年来,全国房价不断上涨,某县2010年4月份的房价平均每平方米为3600元, 比2008年同期的房价平均每平方米上涨了2000元,假设这两年该县房价的平均增长率均为x,则关于x的方程为( )
A.(1+x)2=2000 B.2000(1+x)2=3600
C.(3600-2000)(1+x)=3600 D.(3600-2000)(1+x)2=3600
7.新冠病毒主要是经呼吸道飞沫传播的,在无防护下传播速度很快,已知有1个人患了新冠,经过两轮传染后共有625个人患了新冠,每轮传染中平均一个人传染m人,则m的值为( )
A.20 B.22 C.24 D.25
8.从正方形铁片上截取2cm宽的一个矩形,剩余矩形的面积为80cm2,则原正方形的面积为( )
A.100 cm2 B.121 cm2 C.144 cm2 D.169 cm2
二、填空题
9.若一个数的平方等于这个数的3倍,则这个数为 .
10.现要在一个长为40m,宽为26m的矩形花园中修建等宽的小道,剩余的地方种植花草.如图所示,要使种植花草的面积为864m2,那么小道的宽度应是 m.
11.在一次商品交易会上,参加交易会的每两家公司之间都要签订一份合同,会议结束后统计共签订了78份合同,若设有x家公司出席了这次交易会,则可列方程为: .
12.学校打算用长16m的篱笆围成一个长方形的生物园饲养小动物,生物园的一面靠墙(如图),面积是30m2,求生物园的长和宽.设生物园的宽(与墙相邻的一边)为xm,则列出的方程为 .
13.有长为30m的篱笆,如图所示,一面靠墙(墙足够长),围成中间隔有一道篱笆的长方形花圃,当花圃的面积是72m2时,则AB= .
14.已知两个连续正偶数的积为224,则这两个连续的正偶数是 .
15.一块矩形菜地的面积是120平方米,如果它的长减少2米,那么菜地就变成了正方形,则原矩形的长是 米.
16.用一条长40cm的绳子围成一个面积为64cm2的矩形.设矩形的一边长为xcm,则可列方程为 .
三、解答题
17.将一段铁丝围成面积为 的矩形,且它的长比宽多 ,求矩形的长.
18.如图,某课外活动小组利用一面墙(墙足够长),另三边用20m长的篱笆围成一个面积为50m2的矩形花园ABCD,求边AB、BC的长。
19.青山村种的水稻2001年平均每公顷产7200kg,2003年平均每公顷产8450kg,求水稻每公顷产量的年平均增长率.
20.如图,用两段等长的铁丝恰好可以分别围成一个正五边形和一个正六边形,其中正五边形的边长为(x2+17)cm,正六边形的边长为(x2+2x)cm(其中x>0).求这两段铁丝的总长.
【能力提升】
一、单选题
1.《九章算术》是我国古代的数学名著,书中的“折竹抵地”问题:今有竹高一丈,末折抵地,去本三尺.问折者高几何?意思是:一根竹子,原高一丈(一丈=10尺),一阵风将竹子折断,其竹梢恰好抵地,抵地处离竹子底部3尺远,问折断处离地面的高度是多少?设折断后离地面的高度为x尺,则可列方程为( )
A.x2﹣3=(10﹣x)2 B.x2﹣32=(10﹣x)2
C.x2+3=(10﹣x)2 D.x2+32=(10﹣x)2
2.如图是由三个边长分别是2,3和x的正方形所组成的图形,若直线AB将它分成面积相等的两部分,则x的值是( )
A.1或4 B.2或3 C.3或4 D.1或2
3.某地2015年投入教育经费1200万元,预计2017年投入教育经费3600万元,若每年投入教育经费的年平均增长率为x,则根据题意下列方程正确的是( )
A.1200(1+x)2=3600
B.1200+1200(1+x)+1200(1+x)2=3600
C.1200(1﹣x)2=3600
D.1200(1+x)+1200(1+x)2=3600
4.某中学有一块长30m,宽20m的矩形空地,该中学计划在这块空地。上划出三分之二的区域种花,设计方案如图所示,求花带的宽度。设花带的宽度为xm,则可列方程为( )
A.(30-x)(20-x)= ×20×30
B.(30-2x)(20-x)= ×20×30
C.30x+2×20x= ×20×30
D.(30-2x)(20-x)= ×20×30
5.2019年第一季度,安徽省某企业生产总值比2018年同期增长14%,2020年第一季度受新冠肺炎疫情影响,生产总值比2019年同期减少了9%,设2019年和2020年第一季度生产总值平均增长率为x,则可列方程为( )
A.2x=14%-9%
B.(1+x)2=1+14%-9%
C.(1+x)2=(1+14%)(1-9%)
D.1+2x=(1+14%)(1-9%)
二、填空题
6.一个两位数,它的数值等于它的个位上的数字的平方的3倍,它的十位数字比个位数字大2.若设个位数字为x,列出求该两位数的方程式为 .
7.庆“元旦”,市工会组织篮球比赛,赛制为单循环形式(每两队之间都赛一场),共进行了45场比赛,这次有 队参加比赛
8.根据题意列出方程:有一面积为54m2的长方形,将它的一边剪短5m,另一边剪短2m,恰好变成一个正方形,这个正方形的边长是多少?设正方形的边长为xm,请列出你求解的方程 .
9.一种植物的主干长出若干数目的支干,每个支干又长出同样数目的小分支,主干、支干和小分支的总数是57,每个支干长出 个小分支.
10.一个两位数,个位数字比十位数字大3,个位数的平方恰好等于这个两位数,这个两位数是 .
三、解答题
11.如图所示,学校准备在教学楼后面搭建一简易矩形自行车车棚,一边利用教学楼的后墙(可利用的墙长为 ),另外三边利用学校现有总长 的铁栏围成,留出2米长门供学生进出.若围成的面积为 ,试求出自行车车棚的长和宽.
12.某商场今年二月份的营业额为400万元,三月份由于经营不善,其营业额比二月份下降10%.后来通过加强管理,五月份的营业额达到518.4万元.求三月份到五月份营业额的月平均增长率.
13.如图,某农场有一块长40m, 宽32m的矩形种植地,为方便管理,准备沿平行于两边的方向纵、横各修建一条等宽的小路,要使种植面积为1140m2, 求小路的宽
14.小知识:古希腊的毕达哥拉斯,在2500年前曾经大胆断言,一条线段(AB)的某一短线段(比如AC)与另一长线段(比如BC)之比,如果正好等于另一长线段(比如BC)同整个线段(AB)的比(即 ),那么这样的比例会给人一种美感,后来我们将分割这条线段(AB)的点C称为线段AB的“黄金分割点”.
在主持节目时,主持人站在舞台的黄金分割点处最自然得体,那么在长20米的舞台AB上,主持人从A点到B点走多少米,他的站台最得体?(取 =1.4, =1.7, =2.2)
15.某小区在绿化工程中有一块长为 ,宽为 的矩形空地,计划在其中修建两块相同的矩形绿地,使它们的面积之和为 ,两块绿地之间及周边留有宽度相等的人行通道(如图所示),求人行通道的宽度.
16.在一次酒会上,每两人都只碰一次杯,如果一共碰杯105次,则参加酒会的人数有多少人.
【基础复习答案】
1.【答案】D
【解析】【解答】解:设2018年和2019年第一季度营收入的平均增长率为x,
则可列方程(1+x)2=(1+12%)(1+10%),
故答案为:D.
【分析】设2018年和2019年第一季度营收入的平均增长率为x,再根据企业营收入比2017年同期增长12%,2019年第一季度营收入比2018年同期增长10%,列出方程即可解答
2.【答案】B
【解析】【解答】解:设其中一条直角边的长为x,则另一条直角边的长为(7﹣x),由题意,得
x(7﹣x)=6,
解得:x1=3.,x2=4,
由勾股定理,得
斜边为: =5.
故答案为:B.
【分析】根据直角三角形的面积求出量直角边的长,进而根据勾股定理得出答案。
3.【答案】C
【解析】【解答】从2800吨增加到3090吨,增长年数为2,增长率为x,则方程为:
2800(1+x)2=3090.
故选C.
【分析】本题考查了由实际问题抽象出一元二次方程中的增长率问题.关键是明确增长的基数,增长次数,增长后的值.
4.【答案】B
【解析】【解答】设长方形的长为xcm,则长方形的宽为(20-x)cm,
根据长方形的面积等于长乘以宽可列方程:x(20﹣x)=64,
故答案为:B.
【分析】根据长方形的面积=长×宽可列方程.
5.【答案】C
【解析】【解答】解:有x个球队参加比赛,
根据题意可列方程为:x(x1)=30,
解得:或(舍去);
∴共有6支队伍参赛;
故答案为:C
【分析】根据题意可设有x个球队参加比赛,由此列出方程解之即可。
6.【答案】D
【解析】【分析】2010年的房价为3600元,比2008年的上涨了2000元,即2008年房价为(3600-2000)元,而两年的平均增长率为x,则到了2010年的房价为(3600-2000)(1+x)2元,即3600元,由此可以列出方程式为:
(3600-2000)(1+x)2=3600
故选择D。
【点评】此类题目万变不离其宗,学生可以尝试多做此类题目,将会发现其中的规律。
7.【答案】C
【解析】【解答】由题意,第一轮会有 人被传染,
第二轮会有 人被传染,
则 ,
解得 或 (不符题意,舍去),
故答案为:C.
【分析】根据每轮传染中平均一个人传染m人,分别把第一轮和第二轮被传染的人分别表示出来,再根据两轮过后患者总数为625,列出方程求解即可.
8.【答案】A
【解析】【解答】解:设正方形边长为xcm,依题意得:
x2=2x+80,
解方程得x1=10,x2=﹣8(舍去),
所以正方形的面积是10×10=100(cm2),
故选:A.
【分析】从正方形铁片上截去2cm宽的一个长方形,所截去的长方形的长是正方形的边长,设边长是xcm,即可表示出截取的长方形的面积,根据剩余矩形的面积为80cm2,即正方形的面积=截去的长方形的面积+80cm2.即可列出方程求解.
9.【答案】3或0
【解析】【解答】设这个数是x, =3x
=3x
【分析】设这个数是x,根据一个数的平方等于这个数的3倍,列出方程,求解即可。
10.【答案】2
【解析】【解答】解:设小道的宽为x米,依题意得
(40-2x)(26-x)=864,
解之得
x1=44(舍去),x2=2.
故答案为:2.
【分析】设小道的宽为x米,利用平移的知识知: 种植花草的矩形的长和宽分别为(40-2x)、(26-x),再根据矩形的面积=矩形的长×宽可列关于x的方程,解方程可求解.
11.【答案】 x(x 1)=78
【解析】【解答】解:设有x家公司出席了这次交易会,依题意,得
x(x 1)=78.
故答案为: x(x 1)=78.
【分析】设有x家公司出席了这次交易会,由题意可知每个公司要签订(x-1)份合同,则共签订合同x(x-1)份,结合题意可列方程.
12.【答案】x(16-2x)=30
【解析】【解答】解:由题意得:生物园的长为
则由长方形的面积公式得:x(16-2x)=30
故答案为:x(16-2x)=30.
【分析】由题意得:生物园的长为(16-2x)m,然后利用矩形的面积公式进行解答.
13.【答案】4m或6m
【解析】【解答】解:设AB长为xm,则BC长为(30-3x)m,
根据题意得:x(30-3x)=72,
整理得:x2-10x+24=0,
解得:x1=4,x2=6.
答:AB的长4m或6m.
故答案是:4m或6m.
【分析】根据花圃的面积是72m2,可得x(30-3x)=72,再计算求解即可。
14.【答案】14,16
【解析】【解答】解:设较小的正偶数为x,则较大的正偶数为x+2,根据题意得
x(x+2)=224
解之:x1=14,x2=-16
∵x>0
∴x=14,
∴x+2=16.
故答案为:14,16.
【分析】设较小的正偶数为x,可表示出较大的正偶数,再根据两个连续正偶数的积为224,由此可得到关于x的方程,解方程求出x的值,然后求出这两个连续的正偶数.
15.【答案】12
【解析】【解答】解:∵长减少2m,菜地就变成正方形,
∴设原菜地的长为x米,则宽为(x﹣2)米,
根据题意得:x(x﹣2)=120,
解得:x=12或x=﹣10(舍去),
故答案为:12.
【分析】根据“如果它的长减少2m,那么菜地就变成正方形”可以得到长方形的长比宽多2米,利用矩形的面积公式列出方程即可.
16.【答案】x(20﹣x)=64
【解析】【解答】解:设矩形的一边长为xcm,
∵长方形的周长为40cm,
∴宽为=(20﹣x)(cm),
得x(20﹣x)=64.
故答案为:x(20﹣x)=64.
【分析】本题可根据长方形的周长可以用x表示宽的值,然后根据面积公式即可列出方程.
17.【答案】解:设矩形的长为 cm,则 解得: (不合题意,舍去),答:矩形的长为15cm.
【解析】【分析】实际中矩形的长不可能为负数,所以舍去 .
18.【答案】解:设边AB的长为xm. 根据题意,得 . 解得 . ∴AB=5,BC=20-2×5=10. ∴边AB的长为5m,边BC的长为10 m
【解析】【分析】 设边AB的长为xm ,根据等量关系,列出一元二次方程,即可求解.
19.【答案】解:设水稻每公顷产量的年平均增长率为x,
则有:7200(1+x)2=8450,
解得:x1= ≈0.0833,x2=﹣ =﹣2.0833(应舍去).
∴水稻每公顷产量的年平均增长率为8.33%
【解析】【分析】本题依据题中的等量关系水稻2001年平均每公顷产7200kg,2003年平均每公顷产8450kg,根据增长后的产量=增长前的产量(1+增长率),设增长率是x,则2003年的产量是7200(1+x)2据此即可列方程,解出后检验即可.
20.【答案】解:由已知得,正五边形周长为5(x2+17)cm,正六边形周长为6(x2+2x)cm,
∵正五边形和正六边形的周长相等,
∴5(x2+17)=6(x2+2x),
整理得x2+12x-85=0,配方得(x+6)2=121,
解得x1=5,x2=-17(舍去),
故正五边形的周长为5(52+17)=210(cm).
又因为两段铁丝等长,所以这两段铁丝的总长为420cm.
答:这两段铁丝的总长为420cm.
【解析】【分析】根据正五边形和正六边形的周长相等,列一元二次方程求x的值,得出正六边形的边长,再根据所求边长即可求两段铁丝的总长.
【能力提升答案】
1.【答案】D
【解析】【解答】解:设竹子折断处离地面x尺,则斜边为(10-x)尺,
根据勾股定理得:x2+32=(10-x)2.
故答案为:D
【分析】设竹子折断处离地面x尺,则斜边为(10-x)尺,根据勾股定理建立方程,即可。
2.【答案】D
【解析】【解答】解:如图,补全图形,
∵直线AB将它分成面积相等的两部分,
∴ (2+3+x)×3﹣x(3﹣x)= ×(2+3+x)×3﹣2×1,
解得x=1或x=2,
故答案为:D.
【分析】根据题意列出方程求解即可。
3.【答案】A
【解析】【解答】解: ∵年平均增长率为x,
∴两年后变为原来的 ,
∴可列方程1200(1+x)2=3600
故选A.
4.【答案】B
【解析】【解答】解: 设花带的宽度为xm,
根据题意得:(30-2x)(20-x)= ×20×30,
故答案为:B.
【分析】 设花带的宽度为xm,得出矩形空地的长为(30-2x)m,宽为(20-x)m,根据题意得出矩形空地的面积是原矩形面积的,列出方程即可求解.
5.【答案】C
【解析】【解答】∵2019年的生产总值为(1+14%),
∴2020年的生产总值为(1+14%)(1-9%),
得到方程为(1+x)2=(1+14%)(1-9%),
故答案为:C.
【分析】根据题意得到2019年的生产总值为(1+14%),2020年的生产总值为(1+14%)(1-9%),由此列方程即可.
6.【答案】10(x+2)+x=3x2
【解析】【解答】解:设个位数字为x,则这个数为3x2,十位数字为x+2,
由题意得,10(x+2)+x=3x2.
故答案为10(x+2)+x=3x2.
【分析】设个位数字为x,则这个数为3x2,十位数字为x+2,根据题意表示出这个两位数,列出方程.
7.【答案】10
【解析】【解答】解:设这次有x队参加比赛,则此次比赛的总场数为 场,
根据题意列出方程得: =45,
整理,得:x2-x-90=0,
解得:x1=10,x2=-9(不合题意舍去),
所以,这次有10队参加比赛.
【分析】设这次有x队参加比赛,由于赛制为单循环形式(每两队之间都赛一场),则此次比赛的总场数为 场.根据题意可知:此次比赛的总场数=45场,依此等量关系列出方程求解即可.
8.【答案】(x+5)(x+2)=54
【解析】【解答】解:设正方形的边长为xm,
那么长方形的两边应该为:x+5,x+2,
∴(x+5)(x+2)=54.
故答案为:(x+5)(x+2)=54.
【分析】如果设正方形的边长为xm,那么长方形的两边应该为:x+5,x+2,根据面积相等可列出的方程.
9.【答案】7
【解析】【解答】设每个支干长出x个小分支,
根据题意得: ,
解得: , (不符题意,舍去).
答:每个支干长出7个小分支.
答案是:7.
【分析】设每个支干长出x个小分支,根据主干、支干和小分支的总数是57,列出方程,即可求解.
10.【答案】25或36
【解析】【解答】解:设个位数字为x,那么十位数字是(x-3),这个两位数是10(x-3)+x,
依题意得:
∴
∴
∴x-3=2或3.
答:这个两位数是25或36.
故答案为:25或36.
【分析】设个位数字为x,那么十位数字是(x-3),这个两位数是[10(x-3)+x],然后根据个位数字的平方刚好等于这个两位数即可列出方程求解.
11.【答案】解: 现有总长 的铁栏围成,需留出2米长门
∴设 ,则 ;
根据题意列方程 ,
解得 , ;
当 , (米),
当 , (米),而墙长 ,不合题意舍去,
答:若围成的面积为 ,自行车车棚的长和宽分别为10米,18米.
【解析】【分析】设自行车车棚的宽AB为x米,则长为(38-2x)米,根据矩形的面积公式,即可列方程求解即可.
12.【答案】解:设三月份到五月份营业额的月平均增长率为x,
根据题意得,400×(1-10%)(1+x)2=518.4,
解得,x1=0.2=20%,x2=﹣2.2(不合题意,舍去).
答:三月份到五月份营业额的月平均增长率为20%.
【解析】【分析】设三月份到五月份营业额的月平均增长率为x,则四月份的营业额400×(1-10%)(1+x),五月份的营业额为400×(1-10%)(1+x)2,列出方程求解即可.
13.【答案】解:设小路的宽为xm,依题意有
(40-x)(32-x)=1140,
整理,得x2-72x+140=0.
解得x1=2,x2=70(不合题意,舍去).
答:小路的宽应是2m
【解析】【分析】设小路的宽为xm,采用平移法,可得出种植部分是边长为40-x和32-x的矩形,利用矩形的面积公式建立方程,解方程求出符合题意条件的x(0<x<32)的值。
14.【答案】解:设 ,则 ,
∴由题意得:当 即 ,
∴ ,
解得 , (舍去),
∴此时主持人从A点到B点走 ,
当 即 ,
∴ ,
解得 , (舍去),
∴此时主持人从A点到B点走 ,
∴综上所述,主持人从A点到B点走8m或12m时他的站台最得体.
答:主持人从A点到B点走8m或12m时他的站台最得体.
【解析】【分析】设AC=xm,则BC=(20-x)m,当BC2=AC·AB时,代入求解可得x,进而可得主持人从A点到B点走的距离;当AC2=BC·AB时,同理可得主持人从A点到B点走的距离,据此解答.
15.【答案】解:设人行道的宽度为 米,根据题意得
, (不合题意,舍去)
答:人行道的宽度是 .
【解析】【分析】设人行道的宽度为 米,根据题意列出方程求解即可。
16.【答案】解:设参加酒会的人数为x人,
依题意,得: x(x﹣1)=105,
整理,得:x2﹣x﹣210=0,
解得:x1=15,x2=﹣14(不合题意,舍去).
答:参加酒会的人数有15人
【解析】【分析】设参加酒会的人数为x人,根据每两人都只碰一次杯且一共碰杯105次,即可得出关于x的一元二次方程,解之取其正值即可得出结论.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
