第四章 投影与视图单元测试题(含答案)
文档属性
| 名称 | 第四章 投影与视图单元测试题(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 11.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-07 15:44:51 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第四章综合测试题
(满分:100分 时间:60分钟)
一、选择题(每小题4分,共32分)
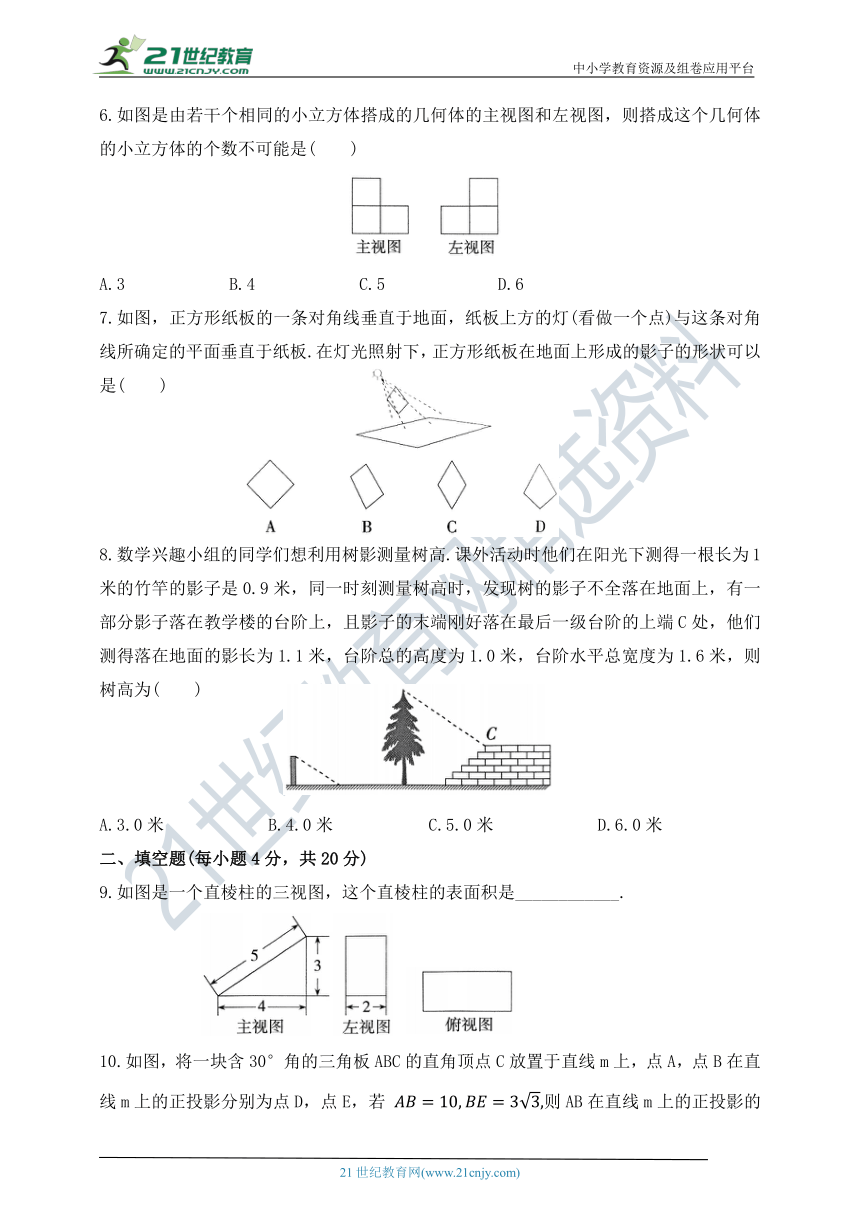
1.如图是小明一天看到的一根电线杆的影子的俯视图,按时间先后顺序排列正确的是 ( )
A.①②③④ B.④③②① C.④③①② D.②③④①
2.如图,是一个底面为等边三角形的正三棱柱,它的主视图是( )
3.小阳和小明两人从远处沿直线走到路灯下,他们规定:小阳在前,小明在后,两人之间的距离始终与小阳的影长相等.在这种情况下,他们两人之间的距离( )
A.始终不变 B.越来越远 C.时近时远 D.越来越近
4.如图所示的几何体的左视图是( )
5.如图,树AB在路灯O的照射下形成投影AC,已知路灯高PO=5m,树影AC=3m,树AB与路灯O的水平距离AP=4.5m,则树的高度AB的长是( )
6.如图是由若干个相同的小立方体搭成的几何体的主视图和左视图,则搭成这个几何体的小立方体的个数不可能是( )
A.3 B.4 C.5 D.6
7.如图,正方形纸板的一条对角线垂直于地面,纸板上方的灯(看做一个点)与这条对角线所确定的平面垂直于纸板.在灯光照射下,正方形纸板在地面上形成的影子的形状可以是( )
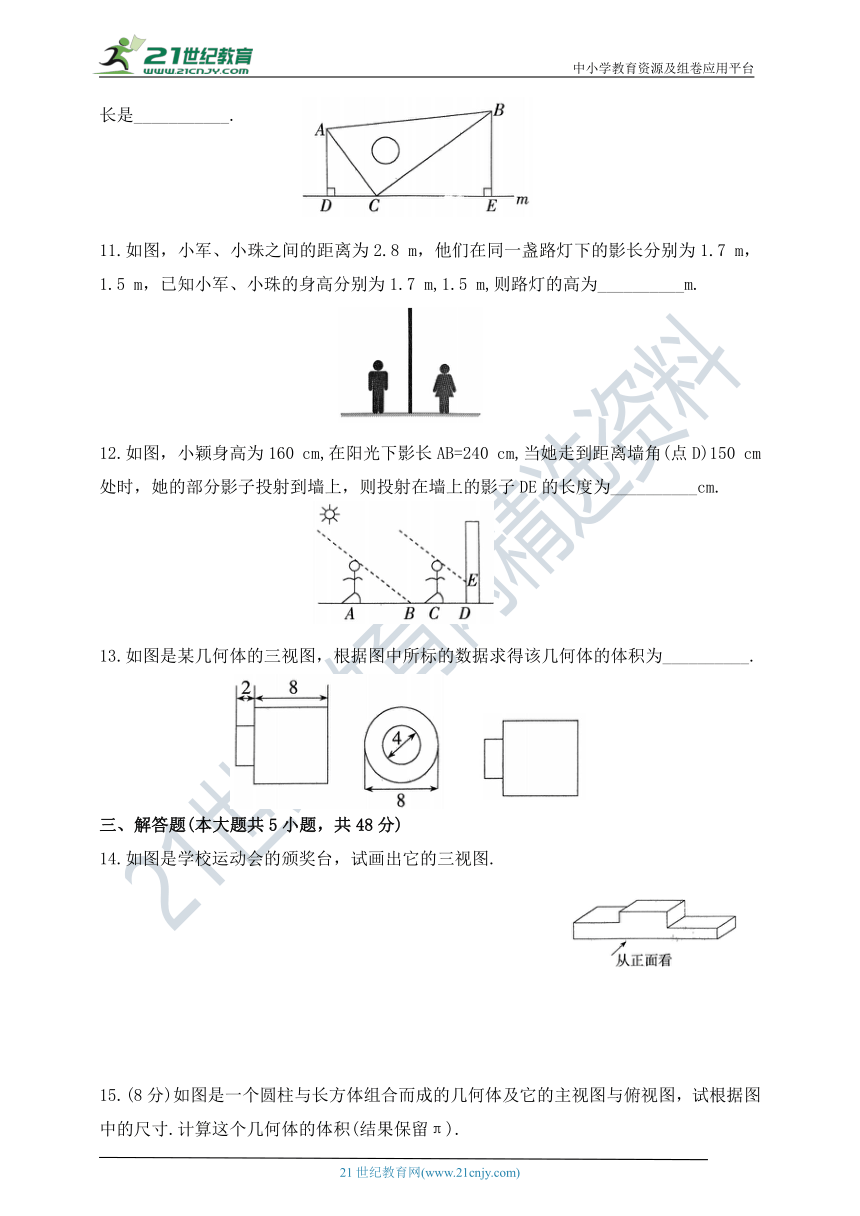
8.数学兴趣小组的同学们想利用树影测量树高.课外活动时他们在阳光下测得一根长为1米的竹竿的影子是0.9米,同一时刻测量树高时,发现树的影子不全落在地面上,有一部分影子落在教学楼的台阶上,且影子的末端刚好落在最后一级台阶的上端C处,他们测得落在地面的影长为1.1米,台阶总的高度为1.0米,台阶水平总宽度为1.6米,则树高为( )
A.3.0米 B.4.0米 C.5.0米 D.6.0米
二、填空题(每小题4分,共20分)
9.如图是一个直棱柱的三视图,这个直棱柱的表面积是____________.
10.如图,将一块含30°角的三角板ABC的直角顶点C放置于直线m上,点A,点B在直线m上的正投影分别为点D,点E,若 则AB在直线m上的正投影的长是___________.
11.如图,小军、小珠之间的距离为2.8 m,他们在同一盏路灯下的影长分别为1.7 m,1.5 m,已知小军、小珠的身高分别为1.7 m,1.5 m,则路灯的高为__________m.
12.如图,小颖身高为160 cm,在阳光下影长AB=240 cm,当她走到距离墙角(点D)150 cm处时,她的部分影子投射到墙上,则投射在墙上的影子DE的长度为__________cm.
13.如图是某几何体的三视图,根据图中所标的数据求得该几何体的体积为__________.
三、解答题(本大题共5小题,共48分)
14.如图是学校运动会的颁奖台,试画出它的三视图.
15.(8分)如图是一个圆柱与长方体组合而成的几何体及它的主视图与俯视图,试根据图中的尺寸.计算这个几何体的体积(结果保留π).
16.(10分)如图,小欣(线段AD)站在灯光下,投在地面上的身影AB=2.4 m,蹲下来(线段
AM),则身影AC=1.05 m,已知小欣的身高AD=1.6 m,蹲下时的高度等于站立高度的一半,求灯离地面的高度PH.
17. (10分)如图,在坡角为30°的山坡上有一铁塔AB,其正前方矗立着一大型广告牌,当阳光与水平线成45°角时,测得铁塔AB落在斜坡上的影子BD的长为6米,落在广告牌上的影子CD的长为4米,求铁塔AB的高(AB,CD均与水平面垂直,结果保留根号).
18.(12分)如图,某光源下有三根杆子,甲杆GH的影子为GM,乙杆EF的影子一部分落在地面上的EA处,一部分落在斜坡AB上的AD处.
(1)请在图中画出形成影子的光线,确定光源所在的位置R,并画出丙杆PQ在地面上的影子;
(2)在(1)的结论下,若过点F的光线FD⊥AB,斜坡与地面的夹角为60°,AD=1米,AE=2米,请求出乙杆EF的高度.(结果保留根号)
参考答案
1.C 从早晨到傍晚太阳光下的影子的指向:西→西北→北→东北→东,由此可判断顺序为④③①②.故选C.
2.A 题图所示的正三棱柱,其主视图是矩形,矩形中间有一条纵向的虚线.故选A.
3.D 因为小阳和小明两人从远处沿直线走到路灯下这一过程中,离光源是由远到近的过程,所以他们在地上的影子会变短,所以他们两人之间的距离越来越近.故选D.
4.A 从几何体的左面看,是两个同心圆.故选A.
5.A ∵AB∥OP,∴△CAB∽△CPO.即 故选A.
6.D 由主视图与左视图,画出俯视图可能的三种情况(数字表示该位置所放小立方体的个数),如图所示,因此搭成这个几何体的小立方体的个数不可能是6,故选D.
7.D ∵正方形纸板的一条对角线垂直于地面,纸板上方的灯(看做一个点)与这条对角线所确定的平面垂直于纸板,∴在地面上的投影关于对角线对称.
∵灯在纸板上方,∴上方投影比下方投影要长.故选D.
8.B 如图,根据同一时刻物高与影长成正比,得
∴AD=3米.∴AB=AD+DB=3+1=4米.故选B.
9.答案 36
解析 由三视图可得这是一个直三棱柱,它的高为2,
这个直三棱柱的底面是直角三角形.
∴这个直三棱柱的表面积为 =36.
10.答案
解析 在Rt△ABC中,∠ABC=30°,AB=10,
在Rt△CBE中,
∵∠CAD+∠ACD=90°,∠BCE+∠ACD=90°,∴∠CAD=∠BCE.
又∠ADC=∠CEB=90°,∴Rt△ACD∽Rt△CBE.
即AB在直线m上的正投影的长是
11.答案 3
解析 如图,由题意可得CD∥AB,MN∥AB,∴△ABE∽△CDE,△ABF∽△MNF.
即 ∴AB=3m.∴路灯的高为3m.
12.答案 60
解析 如图,过E作EF⊥CG于F.
设投射在墙上的影子DE的长度为x cm,由题意得△GFE∽△HAB,
即 解得x=60.
∴投射在墙上的影子DE的长度为60 cm.
13.答案 136π
解析 由三视图知该几何体由大小两个圆柱构成,且处于横放的状态.大圆柱的底面直径为8,高为8;小圆柱的底面直径为4,高为2.故该几何体的体积为π
14.解析 如图所示:
15.解析 由主视图及俯视图可得到数据:圆柱的底面直径为2,高为3;长方体的长、宽、高分别为5、3、1.2.∴这个几何体的体积是 +3π.
16.解析 由题意知AD∥PH,∴△ADB∽△HPB,△AMC∽△HPC.
解得HA=8.4,PH=7.2.
∴灯离地面的高度为7.2m.
17.解析 如图,过点C作CE⊥AB于E,过点B作BF⊥CD于F,
在Rt△BFD中,∵∠DBF=30°,BD=6,
∵AB∥CD,CE⊥AB,BF⊥CD,∴四边形BFCE为矩形,
在Rt△ACE中,
答:铁塔AB的高为 米.
18.解析 (1)如图,QN即为丙杆PQ在地面上的影子.
(2)分别延长FD、EA,交于点S.
在Rt△ADS中,∠ADS=90°,∠DAS=60°,∴∠S=30°.
又∵AD=1,∴AS=2,∴ES=AS+AE=2+2=4.
在Rt△EFS中,∠FES=90°,∠S=30°,
答:乙杆EF的高度为 米.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第四章综合测试题
(满分:100分 时间:60分钟)
一、选择题(每小题4分,共32分)
1.如图是小明一天看到的一根电线杆的影子的俯视图,按时间先后顺序排列正确的是 ( )
A.①②③④ B.④③②① C.④③①② D.②③④①
2.如图,是一个底面为等边三角形的正三棱柱,它的主视图是( )
3.小阳和小明两人从远处沿直线走到路灯下,他们规定:小阳在前,小明在后,两人之间的距离始终与小阳的影长相等.在这种情况下,他们两人之间的距离( )
A.始终不变 B.越来越远 C.时近时远 D.越来越近
4.如图所示的几何体的左视图是( )
5.如图,树AB在路灯O的照射下形成投影AC,已知路灯高PO=5m,树影AC=3m,树AB与路灯O的水平距离AP=4.5m,则树的高度AB的长是( )
6.如图是由若干个相同的小立方体搭成的几何体的主视图和左视图,则搭成这个几何体的小立方体的个数不可能是( )
A.3 B.4 C.5 D.6
7.如图,正方形纸板的一条对角线垂直于地面,纸板上方的灯(看做一个点)与这条对角线所确定的平面垂直于纸板.在灯光照射下,正方形纸板在地面上形成的影子的形状可以是( )
8.数学兴趣小组的同学们想利用树影测量树高.课外活动时他们在阳光下测得一根长为1米的竹竿的影子是0.9米,同一时刻测量树高时,发现树的影子不全落在地面上,有一部分影子落在教学楼的台阶上,且影子的末端刚好落在最后一级台阶的上端C处,他们测得落在地面的影长为1.1米,台阶总的高度为1.0米,台阶水平总宽度为1.6米,则树高为( )
A.3.0米 B.4.0米 C.5.0米 D.6.0米
二、填空题(每小题4分,共20分)
9.如图是一个直棱柱的三视图,这个直棱柱的表面积是____________.
10.如图,将一块含30°角的三角板ABC的直角顶点C放置于直线m上,点A,点B在直线m上的正投影分别为点D,点E,若 则AB在直线m上的正投影的长是___________.
11.如图,小军、小珠之间的距离为2.8 m,他们在同一盏路灯下的影长分别为1.7 m,1.5 m,已知小军、小珠的身高分别为1.7 m,1.5 m,则路灯的高为__________m.
12.如图,小颖身高为160 cm,在阳光下影长AB=240 cm,当她走到距离墙角(点D)150 cm处时,她的部分影子投射到墙上,则投射在墙上的影子DE的长度为__________cm.
13.如图是某几何体的三视图,根据图中所标的数据求得该几何体的体积为__________.
三、解答题(本大题共5小题,共48分)
14.如图是学校运动会的颁奖台,试画出它的三视图.
15.(8分)如图是一个圆柱与长方体组合而成的几何体及它的主视图与俯视图,试根据图中的尺寸.计算这个几何体的体积(结果保留π).
16.(10分)如图,小欣(线段AD)站在灯光下,投在地面上的身影AB=2.4 m,蹲下来(线段
AM),则身影AC=1.05 m,已知小欣的身高AD=1.6 m,蹲下时的高度等于站立高度的一半,求灯离地面的高度PH.
17. (10分)如图,在坡角为30°的山坡上有一铁塔AB,其正前方矗立着一大型广告牌,当阳光与水平线成45°角时,测得铁塔AB落在斜坡上的影子BD的长为6米,落在广告牌上的影子CD的长为4米,求铁塔AB的高(AB,CD均与水平面垂直,结果保留根号).
18.(12分)如图,某光源下有三根杆子,甲杆GH的影子为GM,乙杆EF的影子一部分落在地面上的EA处,一部分落在斜坡AB上的AD处.
(1)请在图中画出形成影子的光线,确定光源所在的位置R,并画出丙杆PQ在地面上的影子;
(2)在(1)的结论下,若过点F的光线FD⊥AB,斜坡与地面的夹角为60°,AD=1米,AE=2米,请求出乙杆EF的高度.(结果保留根号)
参考答案
1.C 从早晨到傍晚太阳光下的影子的指向:西→西北→北→东北→东,由此可判断顺序为④③①②.故选C.
2.A 题图所示的正三棱柱,其主视图是矩形,矩形中间有一条纵向的虚线.故选A.
3.D 因为小阳和小明两人从远处沿直线走到路灯下这一过程中,离光源是由远到近的过程,所以他们在地上的影子会变短,所以他们两人之间的距离越来越近.故选D.
4.A 从几何体的左面看,是两个同心圆.故选A.
5.A ∵AB∥OP,∴△CAB∽△CPO.即 故选A.
6.D 由主视图与左视图,画出俯视图可能的三种情况(数字表示该位置所放小立方体的个数),如图所示,因此搭成这个几何体的小立方体的个数不可能是6,故选D.
7.D ∵正方形纸板的一条对角线垂直于地面,纸板上方的灯(看做一个点)与这条对角线所确定的平面垂直于纸板,∴在地面上的投影关于对角线对称.
∵灯在纸板上方,∴上方投影比下方投影要长.故选D.
8.B 如图,根据同一时刻物高与影长成正比,得
∴AD=3米.∴AB=AD+DB=3+1=4米.故选B.
9.答案 36
解析 由三视图可得这是一个直三棱柱,它的高为2,
这个直三棱柱的底面是直角三角形.
∴这个直三棱柱的表面积为 =36.
10.答案
解析 在Rt△ABC中,∠ABC=30°,AB=10,
在Rt△CBE中,
∵∠CAD+∠ACD=90°,∠BCE+∠ACD=90°,∴∠CAD=∠BCE.
又∠ADC=∠CEB=90°,∴Rt△ACD∽Rt△CBE.
即AB在直线m上的正投影的长是
11.答案 3
解析 如图,由题意可得CD∥AB,MN∥AB,∴△ABE∽△CDE,△ABF∽△MNF.
即 ∴AB=3m.∴路灯的高为3m.
12.答案 60
解析 如图,过E作EF⊥CG于F.
设投射在墙上的影子DE的长度为x cm,由题意得△GFE∽△HAB,
即 解得x=60.
∴投射在墙上的影子DE的长度为60 cm.
13.答案 136π
解析 由三视图知该几何体由大小两个圆柱构成,且处于横放的状态.大圆柱的底面直径为8,高为8;小圆柱的底面直径为4,高为2.故该几何体的体积为π
14.解析 如图所示:
15.解析 由主视图及俯视图可得到数据:圆柱的底面直径为2,高为3;长方体的长、宽、高分别为5、3、1.2.∴这个几何体的体积是 +3π.
16.解析 由题意知AD∥PH,∴△ADB∽△HPB,△AMC∽△HPC.
解得HA=8.4,PH=7.2.
∴灯离地面的高度为7.2m.
17.解析 如图,过点C作CE⊥AB于E,过点B作BF⊥CD于F,
在Rt△BFD中,∵∠DBF=30°,BD=6,
∵AB∥CD,CE⊥AB,BF⊥CD,∴四边形BFCE为矩形,
在Rt△ACE中,
答:铁塔AB的高为 米.
18.解析 (1)如图,QN即为丙杆PQ在地面上的影子.
(2)分别延长FD、EA,交于点S.
在Rt△ADS中,∠ADS=90°,∠DAS=60°,∴∠S=30°.
又∵AD=1,∴AS=2,∴ES=AS+AE=2+2=4.
在Rt△EFS中,∠FES=90°,∠S=30°,
答:乙杆EF的高度为 米.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
