9.4 平行线的判定课件

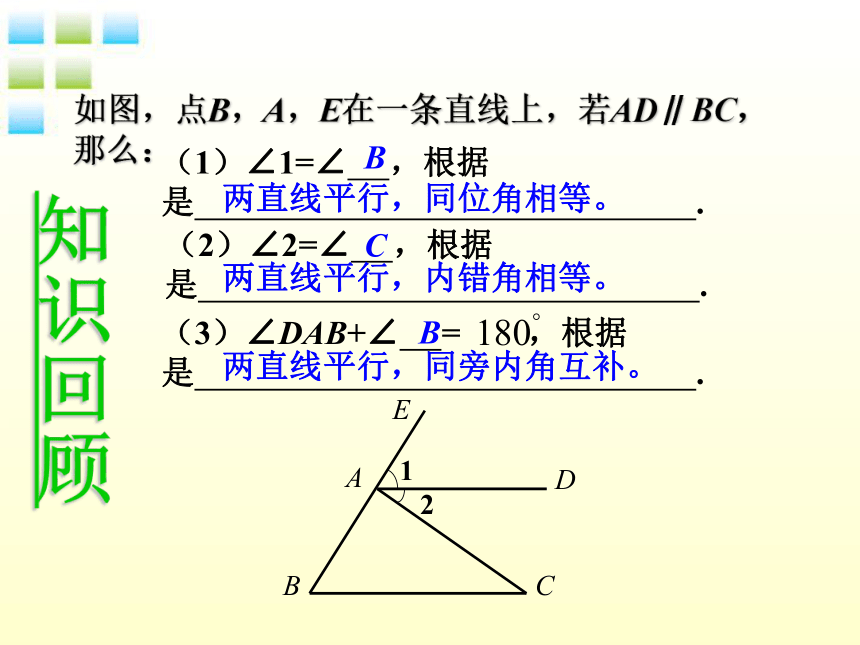
课件19张PPT。9.4平行线的判定知识回顾如图，点B，A，E在一条直线上，若AD∥BC，那么：两直线平行，同位角相等。两直线平行，内错角相等。两直线平行，同旁内角互补。BCB1、经历实验操作、观察、推理、思考、交流等活动，探索并掌握平行线的几种判定方法。
2、能初步运用平行线的判定方法解决一些简单的问题。
3、通过活动进一步发展空间观念和几何直觉，培养推理意识和语言表达能力。
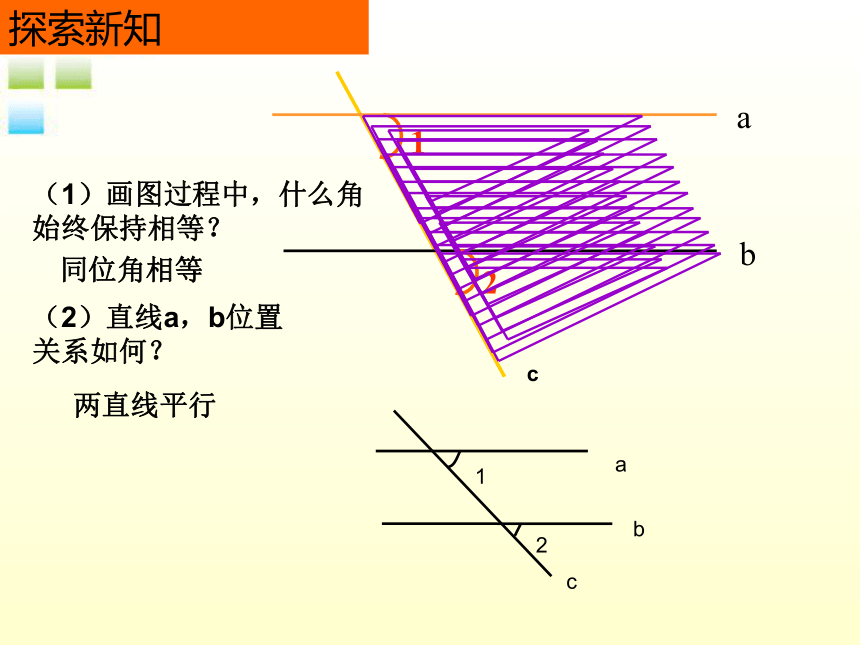
学习目标一、放二、靠三、移四、画回忆画平行线的过程怎样用移动三角尺的方法过线外一点画已知直线的平行线？●探索新知b21ac（1）画图过程中，什么角
始终保持相等？ （2）直线a，b位置
关系如何？ 同位角相等两直线平行简单说成: 同位角相等，两直线平行.两条直线被第三条直线所截，如果同位角相等，那么这两条直线平行.判定两直线平行方法1符号语言：如图∵ ∠1=∠2（已知）
∴ a∥b
（同位角相等，两直线平行） 装修工人正在向墙上钉木条，如果木条b与墙壁的边缘垂直，那么木条a与墙壁的边缘所夹的角为多少度时，才能使木条a与木条b平行？?当∠2=90 °时， ∠1=∠2，
根据同位角相等，两直线平行；
木条a与木条b平行。应用拓展练习1 如图1，∠2＝ ∠1 ，你能得出哪两条直线平行？BE∥CD练习2(1)如图2，∠2＝∠3时，？
(2) ∠1＝ ？时,a∥b .
(3) ∠3＝∠4时, a∥b ?
图2简单说成: 内错角相等，两直线平行.两条直线被第三条直线所截，如果内错角相等，那么这两条直线平行.判定两直线平行方法2符号语言：如图∵ ∠3=∠4（已知）
∴ a∥b
（内错角相等，两直线平行） 交流与发现：如图，∠1与∠2互补，直线a与直线b平行吗？为什么？由此，又得到怎样的方法去判定两条直线平行呢？∴ AB∥CD （同旁内角互补，两直线平行）同旁内角互补，两直线平行。∵ ∠1+∠2=180 °符号语言：两条直线被第三条直线所截，如果同旁内角互补，那么这两条直线平行.例1 如图，直线a,b被c所截，已知∠1＝120°，∠2＝60°，直线a,b平行吗？为什么？ 解：由图可知:
∠3 ＝∠1 =120°（对顶角相等）
∵∠2＝60°
∴∠2＋∠3＝180°
∴a//b（同旁内角互补，两直线平行） 如图，如果CD∥AB，EF∥AB，那么直线CD与直线EF平行吗？你能用我们本节课学习的平行线的判定定理来进行推理证明吗？ 如果两条直线都与第三条直线平行，那么这两条直线平行。思考并交流：注意体会推理哦！试一试 如图，如果∠1=∠A，∠2=∠B，那么直线EF∥DC吗？为什么？ 因为∠2=∠B，所以AB∥DC，（内错角相等，两直线平行。）因为AB∥EF、 AB∥DC，所以EF∥DC。（如果两条直线都与第三条直线平行，那么这两条直线平行。）因为∠1=∠A，所以AB∥EF，（同位角相等，两直线平行。）解：解答1.已知：如图，a⊥c,b⊥c。求证：a∥b。结论：在同一平面内，垂直于同一条直线的两条直线互相平行。 2.如图，AD平分∠BAC， ∠1=∠3，能推出AB∥CD吗？说明理由。3.如图，已知∠MCA= ∠ A， ∠ DEC= ∠ B，那么DE∥MN吗？为什么？加油啊！推理就像走楼梯，要一步一步的逐层递进！2.解：因为 AD平分∠BAC，所以∠1=∠2 （角平分线的定义）又因为 ∠1= ∠3，所以 ∠2= ∠3 （等量代换）所以AB∥CD（内错角相等，两直线平行。）注意哦！推理时可别忘了写上重要的根据啊！1.我们学习了哪些平行线的判定方法？
2. 回忆本节课判定方法的获得过程，我们经历了怎样的基本步骤？ 课堂小结