1.4.2线段的比较与作法(第2课时)课件(共20张PPT)
文档属性
| 名称 | 1.4.2线段的比较与作法(第2课时)课件(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-22 09:47:34 | ||
图片预览







文档简介
1.4 线段的比较与作法(第2课时)
学习目标
1、会用尺子和圆规作一条线段,使它等于已知线段。
2.理解线段和、差的意义,能用直尺和圆规作出线段的和、差。
3、理解线段中点的意义,用刻度尺画出一条线段的中点,并能用准确的数学语言表述,感受符号语言在描述图形中的重要作用.
即学即练
▲探究一
用尺规作线段(和、差)
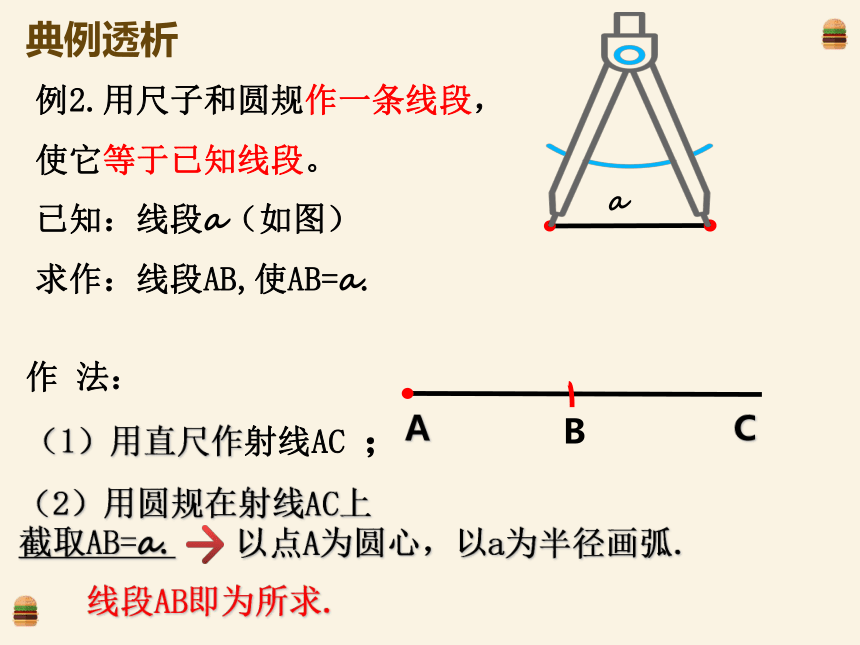
(1)用直尺作射线AC ;
A C
(2)用圆规在射线AC上
截取AB=a.
线段AB即为所求.
作 法:
例2.用尺子和圆规作一条线段,
使它等于已知线段。
已知:线段a(如图)
求作:线段AB,使AB=a.
典例透析
a
B
以点A为圆心,以a为半径画弧.
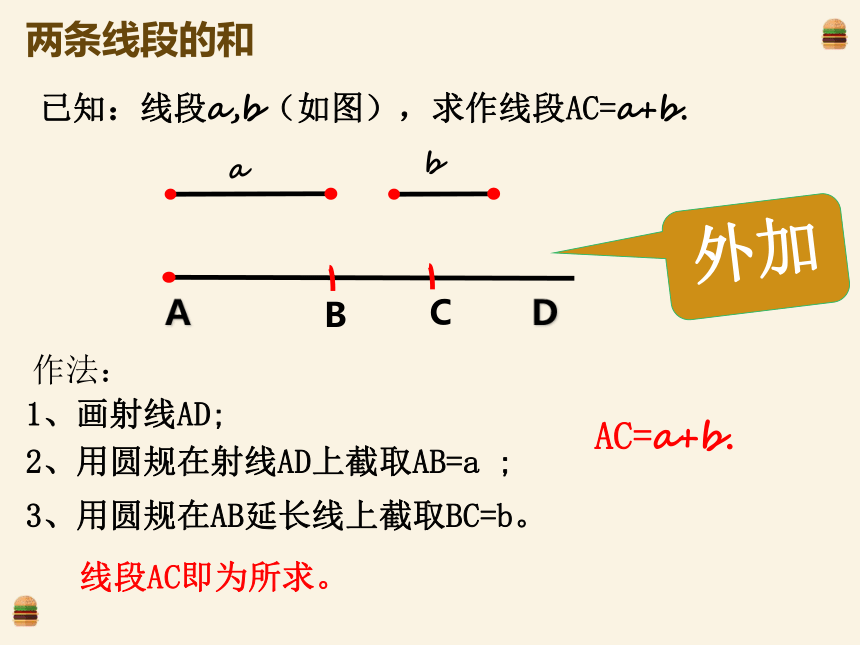
已知:线段a,b(如图),求作线段AC=a+b.
作法:
1、画射线AD;
2、用圆规在射线AD上截取AB=a ;
3、用圆规在AB延长线上截取BC=b。
外加
两条线段的和
a
b
A D
B
C
线段AC即为所求。
AC=a+b.
已知:线段a,b(如图),求作线段AC=a-b.
作法:
1、画射线AD;
2、用圆规在射线AD上截取AB=a ;
3、用圆规在AB上截取BC=b。
内减
两条线段的差
a
b
A D
B
C
线段AC即为所求。
AC=a-b.
1、已知线段a,b,作线段AB,使AB=2a-b.
作法:
线段AB即为所求
小试牛刀
b
a
A C
B
2、如图,填空:
A
B
C
D
(1)AB+BC= ( )
AC
AD - CD=( )
AC
BC=( ) - CD
BD
AD=( ) + ( ) + ( )
AB
BC
CD
小试牛刀
(2)AD=8cm,AC=BD=5cm,则CD等于 cm.
2
▲探究二 线段的中点
想一想
如图所示,要把一根条形木料锯成相等的两段,应从何锯断?
寻找条形木料的中点.
M
B
A
线段的中点
如图所示,如果点 M 把线段 AB 分成相等的两条线段AM与BM, 那么点M叫做线段AB的中点.
这时AM=BM=12 AB ,AB = 2AM=2BM.
?
几何语言
∵M是线段AB的中点
∴AM=BM=?AB 或者 AB=2AM=2BM
总结
1、中点一定在线段上
2、中点将线段分成的两部分一定相等。
即学即练
1、如果点B在线段AC上,那么下列表达式中:
AC=BC、AB=BC、AB=AC、AC=2AB、
AB=12 AC 、 AB+BC=AC。能表示点B是线段AC中点的有 个
?
3
2、如图,已知点C是线段AB的中点,点D是线段AC的中点,完成下列填空:
(1)AB= __ BC ,BC= __ AD
(2)BD= __ AD
(3)已知DC=2cm,则BD= cm.
A
B
C
D
2
2
3
6
线段的等分点
如图,把线段 AB 分成相等的三条线段AM,MN,BM,得到三等分点M,N. 还可以得到四等分点等。
A
B
M
N
∵M,N是线段AB的三等分点
∴AM=MN=BM=?AB
或者AB=3AM=3MN=3BM.
A
B
M
N
P
∵M,N,P是线段AB的四等分点
∴AM=MN=MP=PB=?AB
或者AB=4AM=4MN=4MP=4PB.
小试牛刀
1、如图,已知点C是线段AB的中点,D在线段CB上,DA=10cm,DB=6cm,则线段CD的长为 。
A
B
C
D
2、如图,M,N是AB的三等分点,C为NB中点,且CN=5cm,则AB= cm。
A
B
C
M
N
30
2cm
4、已知线段AB=12cm,点M是它的一个
三等分点, 则AM=___________cm.
4或8
3、线段AB=6厘米,点C在直线AB上,
且BC=3厘米,则线段AC的长为 。
3厘米或9厘米
1.画一条线段等于已知线段,画已知线段的和与差.
2.线段的中点以及等分点(几何语言).
3.线段的计算.—分类讨论
总结
我的收获?
1、己知,如图,点C是线段AB上一点,点M是线段AC的中点,点N是线段BC的中点,如果AC=10cm,BC=4cm,求NM的长。
变式:如图,点C是线段AB上一点,点M是线段AC的中点,点N是线段BC的中点,如果AB=12cm,求NM的长。
能力提升
2、己知,如图,点C是线段AB上一点,点M是线段AB的中点,点N是线段BC的中点,如果AC=10cm,BC=4cm,求NM的长。
A
B
N
C
M
3、已知线段AB上有一点C,点C使AC∶CB=2∶3,且AB=20 cm,点M是线段AC的中点,那么线段AM等于( )
A.2 cm B.4 cm C.6 cm D.8 cm
B
完成20页习题1.4 2,3,5,6题
布置作业
学习目标
1、会用尺子和圆规作一条线段,使它等于已知线段。
2.理解线段和、差的意义,能用直尺和圆规作出线段的和、差。
3、理解线段中点的意义,用刻度尺画出一条线段的中点,并能用准确的数学语言表述,感受符号语言在描述图形中的重要作用.
即学即练
▲探究一
用尺规作线段(和、差)
(1)用直尺作射线AC ;
A C
(2)用圆规在射线AC上
截取AB=a.
线段AB即为所求.
作 法:
例2.用尺子和圆规作一条线段,
使它等于已知线段。
已知:线段a(如图)
求作:线段AB,使AB=a.
典例透析
a
B
以点A为圆心,以a为半径画弧.
已知:线段a,b(如图),求作线段AC=a+b.
作法:
1、画射线AD;
2、用圆规在射线AD上截取AB=a ;
3、用圆规在AB延长线上截取BC=b。
外加
两条线段的和
a
b
A D
B
C
线段AC即为所求。
AC=a+b.
已知:线段a,b(如图),求作线段AC=a-b.
作法:
1、画射线AD;
2、用圆规在射线AD上截取AB=a ;
3、用圆规在AB上截取BC=b。
内减
两条线段的差
a
b
A D
B
C
线段AC即为所求。
AC=a-b.
1、已知线段a,b,作线段AB,使AB=2a-b.
作法:
线段AB即为所求
小试牛刀
b
a
A C
B
2、如图,填空:
A
B
C
D
(1)AB+BC= ( )
AC
AD - CD=( )
AC
BC=( ) - CD
BD
AD=( ) + ( ) + ( )
AB
BC
CD
小试牛刀
(2)AD=8cm,AC=BD=5cm,则CD等于 cm.
2
▲探究二 线段的中点
想一想
如图所示,要把一根条形木料锯成相等的两段,应从何锯断?
寻找条形木料的中点.
M
B
A
线段的中点
如图所示,如果点 M 把线段 AB 分成相等的两条线段AM与BM, 那么点M叫做线段AB的中点.
这时AM=BM=12 AB ,AB = 2AM=2BM.
?
几何语言
∵M是线段AB的中点
∴AM=BM=?AB 或者 AB=2AM=2BM
总结
1、中点一定在线段上
2、中点将线段分成的两部分一定相等。
即学即练
1、如果点B在线段AC上,那么下列表达式中:
AC=BC、AB=BC、AB=AC、AC=2AB、
AB=12 AC 、 AB+BC=AC。能表示点B是线段AC中点的有 个
?
3
2、如图,已知点C是线段AB的中点,点D是线段AC的中点,完成下列填空:
(1)AB= __ BC ,BC= __ AD
(2)BD= __ AD
(3)已知DC=2cm,则BD= cm.
A
B
C
D
2
2
3
6
线段的等分点
如图,把线段 AB 分成相等的三条线段AM,MN,BM,得到三等分点M,N. 还可以得到四等分点等。
A
B
M
N
∵M,N是线段AB的三等分点
∴AM=MN=BM=?AB
或者AB=3AM=3MN=3BM.
A
B
M
N
P
∵M,N,P是线段AB的四等分点
∴AM=MN=MP=PB=?AB
或者AB=4AM=4MN=4MP=4PB.
小试牛刀
1、如图,已知点C是线段AB的中点,D在线段CB上,DA=10cm,DB=6cm,则线段CD的长为 。
A
B
C
D
2、如图,M,N是AB的三等分点,C为NB中点,且CN=5cm,则AB= cm。
A
B
C
M
N
30
2cm
4、已知线段AB=12cm,点M是它的一个
三等分点, 则AM=___________cm.
4或8
3、线段AB=6厘米,点C在直线AB上,
且BC=3厘米,则线段AC的长为 。
3厘米或9厘米
1.画一条线段等于已知线段,画已知线段的和与差.
2.线段的中点以及等分点(几何语言).
3.线段的计算.—分类讨论
总结
我的收获?
1、己知,如图,点C是线段AB上一点,点M是线段AC的中点,点N是线段BC的中点,如果AC=10cm,BC=4cm,求NM的长。
变式:如图,点C是线段AB上一点,点M是线段AC的中点,点N是线段BC的中点,如果AB=12cm,求NM的长。
能力提升
2、己知,如图,点C是线段AB上一点,点M是线段AB的中点,点N是线段BC的中点,如果AC=10cm,BC=4cm,求NM的长。
A
B
N
C
M
3、已知线段AB上有一点C,点C使AC∶CB=2∶3,且AB=20 cm,点M是线段AC的中点,那么线段AM等于( )
A.2 cm B.4 cm C.6 cm D.8 cm
B
完成20页习题1.4 2,3,5,6题
布置作业
同课章节目录
- 第1章 基本的几何图形
- 1.1 我们身边的图形世界
- 1.2 几何图形
- 1.3 线段、射线和直线
- 1.4 线段的比较与作法
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数与绝对值
- 第3章 有理数的运算
- 3.1 有理数的加法与减法
- 3.2 有理数的乘法与除法
- 3.3 有理数的乘方
- 3.4 有理数的混合运算
- 3.5 利用计算器进行有理数的计算
- 第4章 数据的收集整理与描述
- 4.1 普查和抽样调查
- 4.2 简单随机抽样
- 4.3 数据的整理
- 4.4 扇形统计图
- 第5章 代数式与函数的初步认识
- 5.1 用字母表示数
- 5.2 代数式
- 5.3 代数式的值
- 5.4 生活中的常量与变量
- 5.5 函数的初步认识
- 第6章 整式的加减
- 6.1 单项式与多项式
- 6.2 同类项
- 6.3 去括号
- 6.4 整式的加减
- 第7章 一元一次方程
- 7.1 等式的基本性质
- 7.2 一元一次方程
- 7.3 一元一次方程的解法
- 7.4 一元一次方程的应用
