2.2圆的对称性(第1课时) 课件(共24张PPT)
文档属性
| 名称 | 2.2圆的对称性(第1课时) 课件(共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-05 00:00:00 | ||
图片预览




文档简介
(共24张PPT)
苏科版 九年级上册
2.2 圆的对称性
第1课时 圆的对称性
学习目标
1.理解圆的对称性(轴对称)及有关的性质;
2.探索圆心角、弧、弦之间关系定理并利用其解决相关问
题;
3.理解圆心角、弧、弦之间关系定理中的“在同圆或等圆”
条件的意义.
导入新课
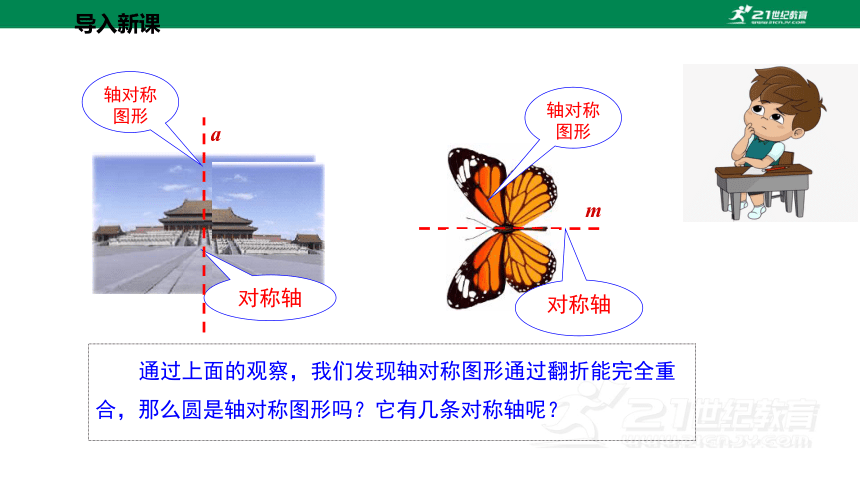
通过上面的观察,我们发现轴对称图形通过翻折能完全重合,那么圆是轴对称图形吗?它有几条对称轴呢?
轴对称图形
轴对称图形
对称轴
对称轴
a
m
导入新课
观察图形
导入新课
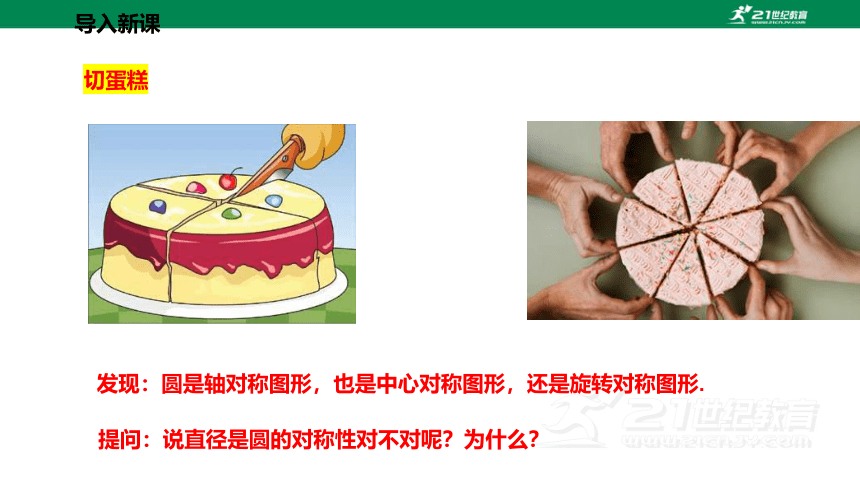
切蛋糕
发现:圆是轴对称图形,也是中心对称图形,还是旋转对称图形.
提问:说直径是圆的对称性对不对呢?为什么?
讲授新课
知识点一 圆的对称性
(1)圆是否是轴对称图形?如果是,它的对称轴是什么?对称轴又有多少条?
(2)想一想,你用什么方法可以证明呢?
圆的对称性:
圆是轴对称图形,其对称轴是任意一条过圆心的直线,也可以说是直径所在的直线;
用折叠的方法
●O
回答问题
讲授新课
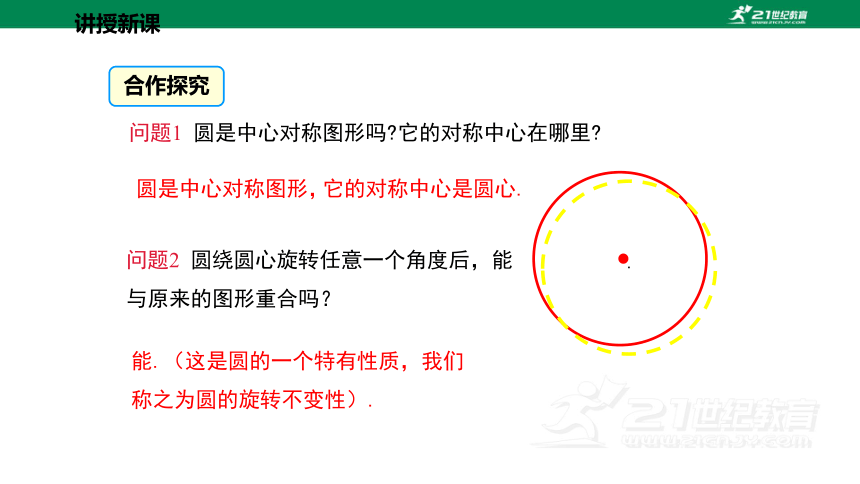
问题1 圆是中心对称图形吗 它的对称中心在哪里
·
圆是中心对称图形,
它的对称中心是圆心.
问题2 圆绕圆心旋转任意一个角度后,能与原来的图形重合吗?
能.(这是圆的一个特有性质,我们称之为圆的旋转不变性).
合作探究
讲授新课
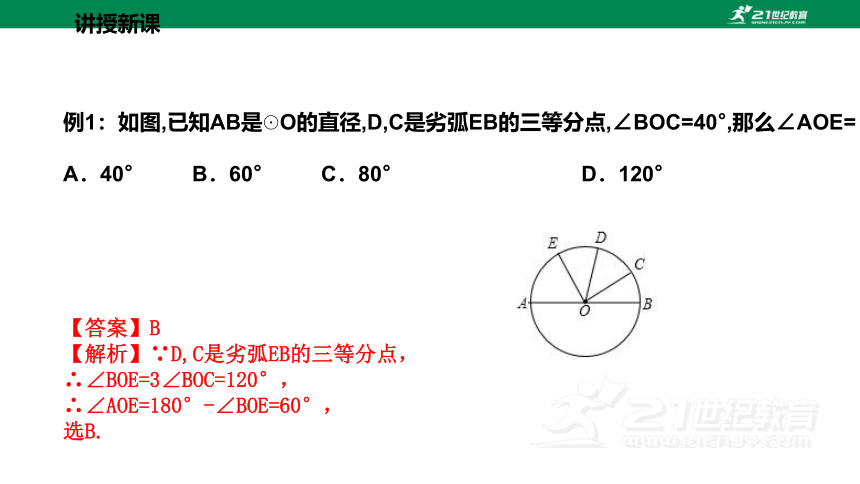
例1:如图,已知AB是☉O的直径,D,C是劣弧EB的三等分点,∠BOC=40°,那么∠AOE= ( )
A.40° B.60° C.80° D.120°
【答案】B
【解析】∵D,C是劣弧EB的三等分点,
∴∠BOE=3∠BOC=120°,
∴∠AOE=180°-∠BOE=60°,
选B.
讲授新课
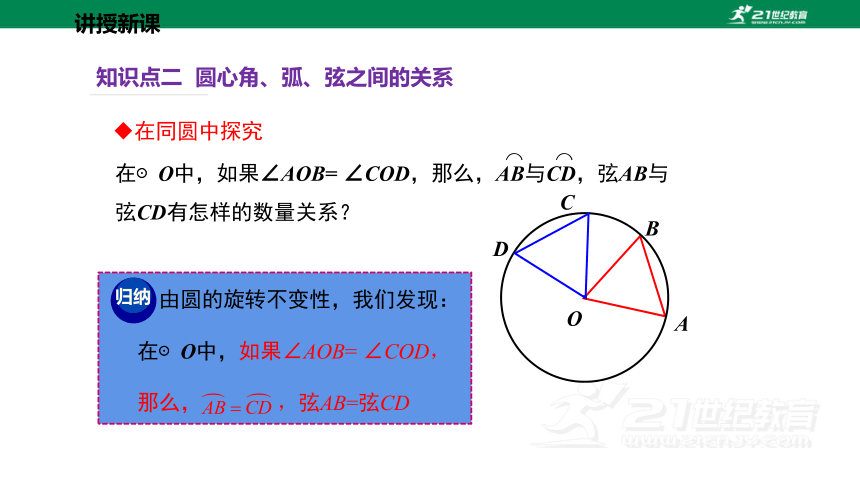
知识点二 圆心角、弧、弦之间的关系
在同圆中探究
在⊙O中,如果∠AOB= ∠COD,那么,AB与CD,弦AB与弦CD有怎样的数量关系?
⌒
⌒
C
·
O
A
B
D
由圆的旋转不变性,我们发现:
在⊙O中,如果∠AOB= ∠COD,
那么, ,弦AB=弦CD
归纳
讲授新课
·
O
A
B
如图,在等圆中,如果∠AOB=∠CO ′ D,你发现的等量关系是否依然成立?为什么?
·
O ′
C
D
在等圆中探究
通过平移和旋转将两个等圆变成同一个圆,我们发现:如果∠AOB=∠COD,那么,AB=CD,弦AB=弦CD.
归纳
⌒
⌒
概念归纳
在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等.
①∠AOB=∠COD
②AB=CD
⌒ ⌒
③AB=CD
A
B
O
D
C
要点归纳
在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等.
弧、弦与圆心角关系定理的推论
典型例题
例1 如图,AB,DE是⊙O 的直径,C是⊙O 上的一点,
且AD=CE.BE和CE的大小有什么关系?为什么?
·
E
B
C
O
A
D
解:BE=CE.理由是:
∵∠AOD=∠BOE,
∴AD=BE.
又∵AD=CE,
∴BE=CE.
∴BE=CE.
⌒ ⌒
⌒ ⌒
⌒ ⌒
⌒ ⌒
练一练
1、判断下列说法是否正确:
相等的圆心角所对的弧相等。( )
相等的弧所对的弦相等。( )
相等的弦所对的弧相等。( )
2、如图,⊙O中,AB=CD,
,则
O
D
C
A
B
1
2
×
√
50
o
×
练一练
3、下列命题中正确的有( )
①弦是圆上任意两点之间的部分;②半径是弦;③直径是最长的弦;④弧是半圆,半圆是弧.
A.1个 B.2个 C.3个 D.4个
【答案】A
【解析】①弦是圆上任意两点之间的连线段,所以①错误;
②半径不是弦,所以②错误;
③直径是最长的弦,正确;④弧是半圆,只有180°的弧才是半圆,所以④错误,故选A.
当堂检测
1、判断:
(1)直径是弦,弦是直径(_____)
(2)半圆是圆弧(_____)
(3)长度相等的弧是等弧(_____)
(4)能够重合的弧是等弧(_____)
(5)圆弧分为优弧和劣弧(_____)
(6)优弧一定大于劣弧 (_____)
(7)半径相等的圆是等圆 (_____)
【答案】 × √ × × × × √
【详解】(1)直径是弦,弦不一定是是直径,故错误;
(2)半圆是圆弧,正确;
(3)能完全重合的弧是等弧,故错误;
(4)能够完全重合的弧是等弧,故错误;
(5)圆弧分为优弧和劣弧和半圆,故错误;
(6)同圆或等圆中,优弧一定大于劣弧,故错误;
(7)半径相等的圆是等圆,正确.
当堂检测
2、如图,点A、B、C在⊙O上,∠ABO=22°,∠ACO=42°,则∠BOC等于( )
A.128° B.108° C.86° D.64°
【答案】A
【分析】先过A作⊙O的直径,交⊙O于D,
将∠BOC分为两个角,利用圆的半径相等及
外角定理求出每个角的度数,相加即可得到
∠BOC的度数.
【解析】过A作⊙O的直径,交⊙O于D;
在△OAB中,OA=OB,则∠BOD=∠ABO+∠OAB
=2×22°=44°,
同理可得:∠COD=∠ACO+∠OAC=2×42°=84°,
故∠BOC=∠BOD+∠COD=128°。故选:A.
当堂检测
3、如图,⊙O的直径为10,弦AB=8,P是弦AB上的一个动点,那么OP的长的取值范围是 .
【答案】3≤OP≤5.
【解析】OP最长边应是半径长,为5;
根据垂线段最短,可得到当OP⊥AB时,OP最短.
∵直径为10,弦AB=8,
∴∠OPA=90°,OA=5,
由圆的对称性得AP=4,由勾股定理的OP=5,
∴OP最短为3,
∴OP的长的取值范围是3≤OP≤5.
当堂检测
4、如图,AB是⊙O的直径,∠AOE=78°,点C、D是弧BE的三等分点,则∠COE=_____.
【答案】68°
【解析】∵∠AOE=78°,
∴劣弧的度数为78°.
∵AB是⊙O的直径,
∴劣弧的度数为180°﹣78°=102°.
∵点C、D是弧BE的三等分点,
∴∠COE=102°=68°.
故答案为:68°.
当堂检测
5、将一个圆分割成三个扇形,使它们圆心角度数比为2:3:4,则这3个圆心角中度数最大的为________
【答案】160°
【解析】将一个圆分割成三个扇形,它们的圆心角的和为360°,再由三个圆心角的度数比为2:3:4,可求出最大的圆心角度数:360°×=160°.故答案是:160°.
当堂检测
6、如图,在⊙O中,2∠AOB=∠COD,那么CD=2AB成立吗?CD=2AB也成立吗?请说明理由;如不是,那它们之间的关系又是什么?
⌒ ⌒
答:CD=2AB成立,CD=2AB不成立.不是,取 的中点E,连接OE.那么∠AOB=∠COE=∠DOE,所以 = = . =2 ,弦AB=CE=DE,在△CDE中,CE+DE>CD,即CD<2AB.
⌒ ⌒
A
B
C
D
E
O
课堂小结
1.圆是中心对称图形,圆心是它的对称中心.
2.在同圆或等圆中,如果两个圆心角,两条弧,两条弦中有一组量相等,那么它们所对应的其余各组都分别相等.
3.圆心角的度数与它所对的弧的度数相等.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
苏科版 九年级上册
2.2 圆的对称性
第1课时 圆的对称性
学习目标
1.理解圆的对称性(轴对称)及有关的性质;
2.探索圆心角、弧、弦之间关系定理并利用其解决相关问
题;
3.理解圆心角、弧、弦之间关系定理中的“在同圆或等圆”
条件的意义.
导入新课
通过上面的观察,我们发现轴对称图形通过翻折能完全重合,那么圆是轴对称图形吗?它有几条对称轴呢?
轴对称图形
轴对称图形
对称轴
对称轴
a
m
导入新课
观察图形
导入新课
切蛋糕
发现:圆是轴对称图形,也是中心对称图形,还是旋转对称图形.
提问:说直径是圆的对称性对不对呢?为什么?
讲授新课
知识点一 圆的对称性
(1)圆是否是轴对称图形?如果是,它的对称轴是什么?对称轴又有多少条?
(2)想一想,你用什么方法可以证明呢?
圆的对称性:
圆是轴对称图形,其对称轴是任意一条过圆心的直线,也可以说是直径所在的直线;
用折叠的方法
●O
回答问题
讲授新课
问题1 圆是中心对称图形吗 它的对称中心在哪里
·
圆是中心对称图形,
它的对称中心是圆心.
问题2 圆绕圆心旋转任意一个角度后,能与原来的图形重合吗?
能.(这是圆的一个特有性质,我们称之为圆的旋转不变性).
合作探究
讲授新课
例1:如图,已知AB是☉O的直径,D,C是劣弧EB的三等分点,∠BOC=40°,那么∠AOE= ( )
A.40° B.60° C.80° D.120°
【答案】B
【解析】∵D,C是劣弧EB的三等分点,
∴∠BOE=3∠BOC=120°,
∴∠AOE=180°-∠BOE=60°,
选B.
讲授新课
知识点二 圆心角、弧、弦之间的关系
在同圆中探究
在⊙O中,如果∠AOB= ∠COD,那么,AB与CD,弦AB与弦CD有怎样的数量关系?
⌒
⌒
C
·
O
A
B
D
由圆的旋转不变性,我们发现:
在⊙O中,如果∠AOB= ∠COD,
那么, ,弦AB=弦CD
归纳
讲授新课
·
O
A
B
如图,在等圆中,如果∠AOB=∠CO ′ D,你发现的等量关系是否依然成立?为什么?
·
O ′
C
D
在等圆中探究
通过平移和旋转将两个等圆变成同一个圆,我们发现:如果∠AOB=∠COD,那么,AB=CD,弦AB=弦CD.
归纳
⌒
⌒
概念归纳
在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等.
①∠AOB=∠COD
②AB=CD
⌒ ⌒
③AB=CD
A
B
O
D
C
要点归纳
在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等.
弧、弦与圆心角关系定理的推论
典型例题
例1 如图,AB,DE是⊙O 的直径,C是⊙O 上的一点,
且AD=CE.BE和CE的大小有什么关系?为什么?
·
E
B
C
O
A
D
解:BE=CE.理由是:
∵∠AOD=∠BOE,
∴AD=BE.
又∵AD=CE,
∴BE=CE.
∴BE=CE.
⌒ ⌒
⌒ ⌒
⌒ ⌒
⌒ ⌒
练一练
1、判断下列说法是否正确:
相等的圆心角所对的弧相等。( )
相等的弧所对的弦相等。( )
相等的弦所对的弧相等。( )
2、如图,⊙O中,AB=CD,
,则
O
D
C
A
B
1
2
×
√
50
o
×
练一练
3、下列命题中正确的有( )
①弦是圆上任意两点之间的部分;②半径是弦;③直径是最长的弦;④弧是半圆,半圆是弧.
A.1个 B.2个 C.3个 D.4个
【答案】A
【解析】①弦是圆上任意两点之间的连线段,所以①错误;
②半径不是弦,所以②错误;
③直径是最长的弦,正确;④弧是半圆,只有180°的弧才是半圆,所以④错误,故选A.
当堂检测
1、判断:
(1)直径是弦,弦是直径(_____)
(2)半圆是圆弧(_____)
(3)长度相等的弧是等弧(_____)
(4)能够重合的弧是等弧(_____)
(5)圆弧分为优弧和劣弧(_____)
(6)优弧一定大于劣弧 (_____)
(7)半径相等的圆是等圆 (_____)
【答案】 × √ × × × × √
【详解】(1)直径是弦,弦不一定是是直径,故错误;
(2)半圆是圆弧,正确;
(3)能完全重合的弧是等弧,故错误;
(4)能够完全重合的弧是等弧,故错误;
(5)圆弧分为优弧和劣弧和半圆,故错误;
(6)同圆或等圆中,优弧一定大于劣弧,故错误;
(7)半径相等的圆是等圆,正确.
当堂检测
2、如图,点A、B、C在⊙O上,∠ABO=22°,∠ACO=42°,则∠BOC等于( )
A.128° B.108° C.86° D.64°
【答案】A
【分析】先过A作⊙O的直径,交⊙O于D,
将∠BOC分为两个角,利用圆的半径相等及
外角定理求出每个角的度数,相加即可得到
∠BOC的度数.
【解析】过A作⊙O的直径,交⊙O于D;
在△OAB中,OA=OB,则∠BOD=∠ABO+∠OAB
=2×22°=44°,
同理可得:∠COD=∠ACO+∠OAC=2×42°=84°,
故∠BOC=∠BOD+∠COD=128°。故选:A.
当堂检测
3、如图,⊙O的直径为10,弦AB=8,P是弦AB上的一个动点,那么OP的长的取值范围是 .
【答案】3≤OP≤5.
【解析】OP最长边应是半径长,为5;
根据垂线段最短,可得到当OP⊥AB时,OP最短.
∵直径为10,弦AB=8,
∴∠OPA=90°,OA=5,
由圆的对称性得AP=4,由勾股定理的OP=5,
∴OP最短为3,
∴OP的长的取值范围是3≤OP≤5.
当堂检测
4、如图,AB是⊙O的直径,∠AOE=78°,点C、D是弧BE的三等分点,则∠COE=_____.
【答案】68°
【解析】∵∠AOE=78°,
∴劣弧的度数为78°.
∵AB是⊙O的直径,
∴劣弧的度数为180°﹣78°=102°.
∵点C、D是弧BE的三等分点,
∴∠COE=102°=68°.
故答案为:68°.
当堂检测
5、将一个圆分割成三个扇形,使它们圆心角度数比为2:3:4,则这3个圆心角中度数最大的为________
【答案】160°
【解析】将一个圆分割成三个扇形,它们的圆心角的和为360°,再由三个圆心角的度数比为2:3:4,可求出最大的圆心角度数:360°×=160°.故答案是:160°.
当堂检测
6、如图,在⊙O中,2∠AOB=∠COD,那么CD=2AB成立吗?CD=2AB也成立吗?请说明理由;如不是,那它们之间的关系又是什么?
⌒ ⌒
答:CD=2AB成立,CD=2AB不成立.不是,取 的中点E,连接OE.那么∠AOB=∠COE=∠DOE,所以 = = . =2 ,弦AB=CE=DE,在△CDE中,CE+DE>CD,即CD<2AB.
⌒ ⌒
A
B
C
D
E
O
课堂小结
1.圆是中心对称图形,圆心是它的对称中心.
2.在同圆或等圆中,如果两个圆心角,两条弧,两条弦中有一组量相等,那么它们所对应的其余各组都分别相等.
3.圆心角的度数与它所对的弧的度数相等.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
