2.4圆周角(第1课时) 课件(共33张PPT)
文档属性
| 名称 | 2.4圆周角(第1课时) 课件(共33张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-05 17:56:18 | ||
图片预览





文档简介
(共33张PPT)
苏科版 九年级上册
2.4 圆周角
第1课时 圆周角与圆心角的关系
学习目标
1.结合图形了解圆心角、圆周角的概念和区别;会叙述并且证明圆周角定理;
2.利用圆心角与圆周角的关系解决与圆相关的几何问题;
3.熟练掌握圆周角定理的推论,并学会其证明过程与应用;
当堂检测
知识回顾
1.什么叫圆心角
.
O
A
B
顶点在圆心的角叫圆心角
2. 圆心角、弧、弦三个量之间关系的一个结论,这个结论是什么?
在同圆(或等圆)中,如果圆心角、弧、弦有一组量相等,那么它们所对应的其余两个量都分别相等.
导入新课
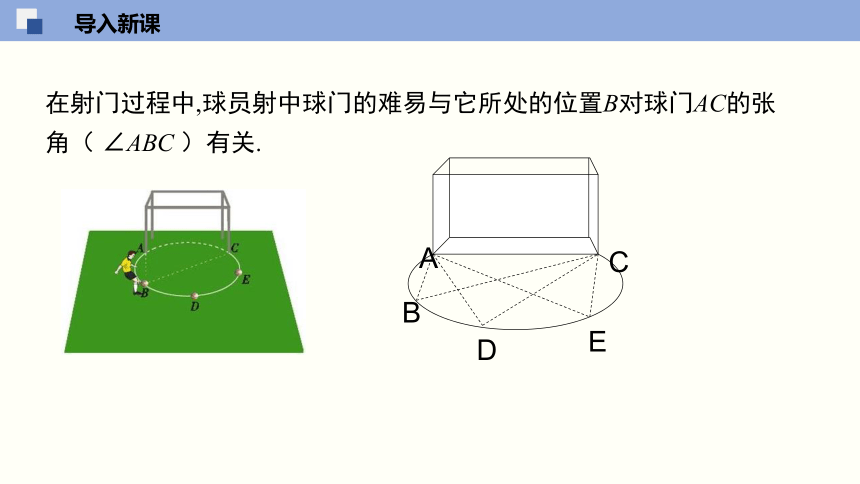
在射门过程中,球员射中球门的难易与它所处的位置B对球门AC的张角( ∠ABC )有关.
A
B
C
D
E
导入新课
各抒己见:图中的∠ABC、∠ADC和∠AEC的顶点各在圆的什么位置?它们的两边和圆是什么关系?
顶点在☉O上,角的两边分别与☉O相交.
再思考一下:∠ABC、∠ADC和∠AEC的度数有什么关系呢?
讲授新课
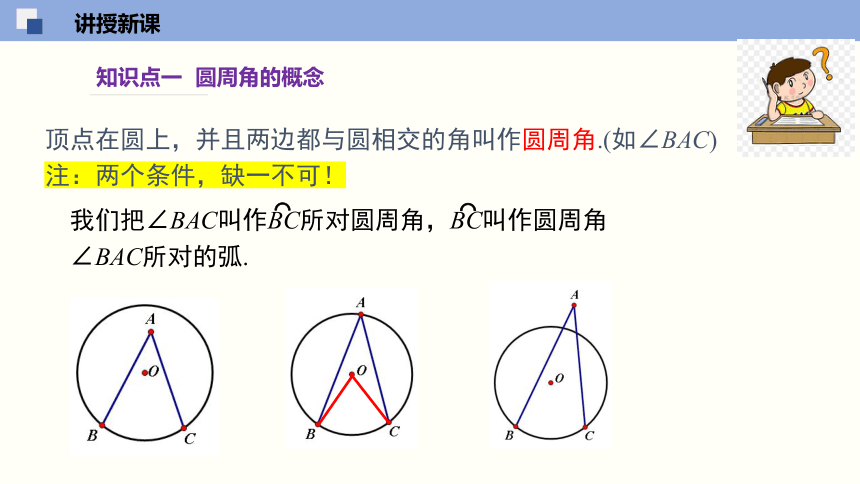
知识点一 圆周角的概念
顶点在圆上,并且两边都与圆相交的角叫作圆周角.(如∠BAC)
注:两个条件,缺一不可!
我们把∠BAC叫作BC所对圆周角,BC叫作圆周角∠BAC所对的弧.
⌒
⌒
讲授新课
圆周角在我们生活中处处可见,比如,我们从团旗上的图案抽象出如图所示图形,图形中就有很多圆周角.
E
·
A
O
D
B
C
典型例题
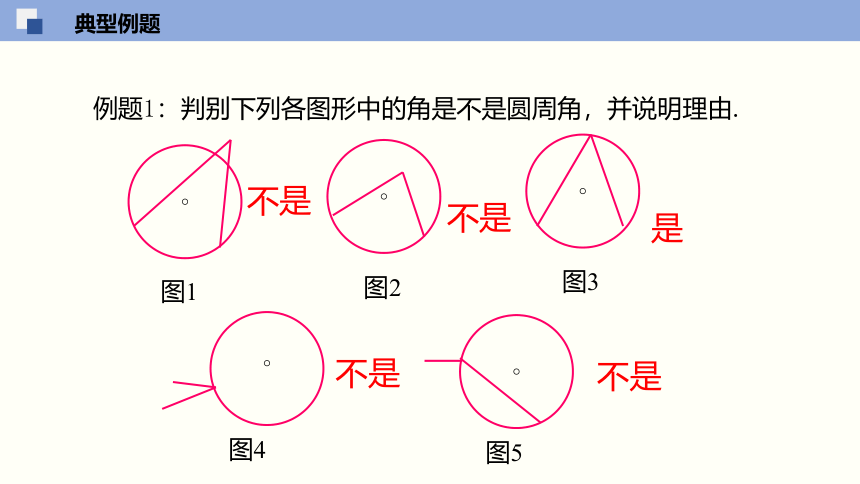
例题1:判别下列各图形中的角是不是圆周角,并说明理由.
不是
不是
是
不是
不是
图1
图2
图3
图4
图5
练一练
·
C
O
A
B
·
C
O
B
·
C
O
B
A
A
·
C
O
A
B
·
C
O
B
·
C
O
B
A
A
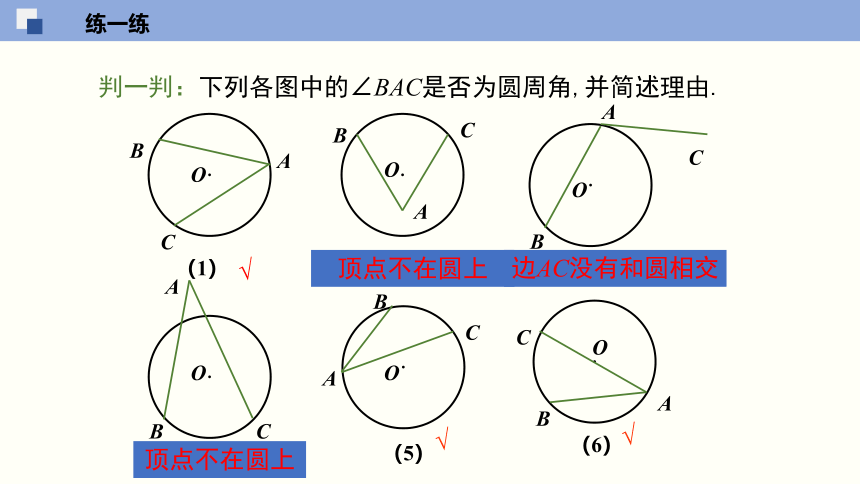
判一判:下列各图中的∠BAC是否为圆周角,并简述理由.
(2)
(1)
(3)
(5)
(6)
顶点不在圆上
顶点不在圆上
边AC没有和圆相交
√
√
√
讲授新课
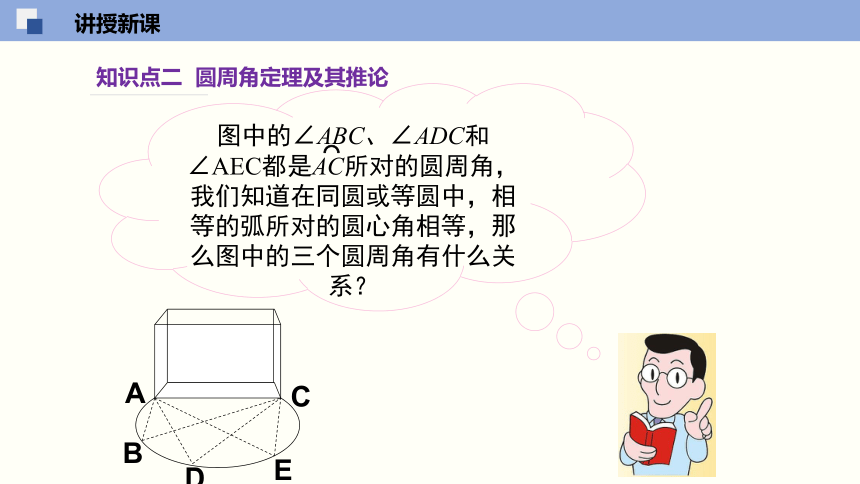
知识点二 圆周角定理及其推论
图中的∠ABC、∠ADC和∠AEC都是AC所对的圆周角,我们知道在同圆或等圆中,相等的弧所对的圆心角相等,那么图中的三个圆周角有什么关系?
⌒
A
B
C
D
E
讲授新课
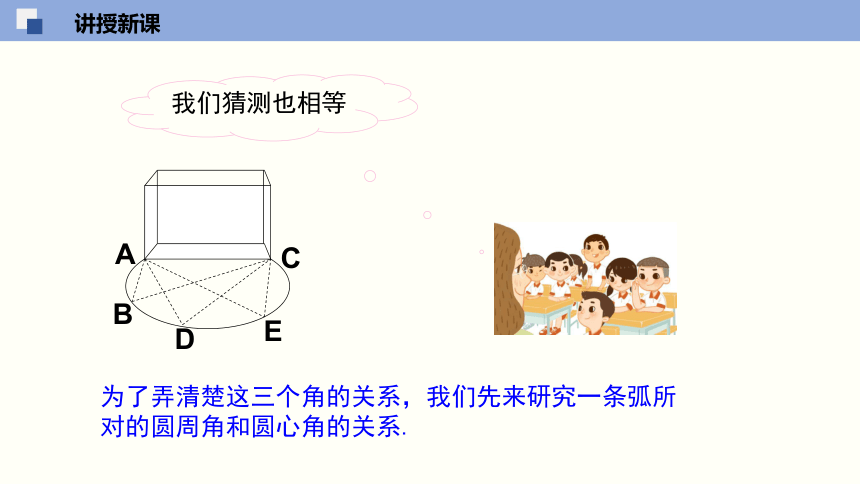
为了弄清楚这三个角的关系,我们先来研究一条弧所对的圆周角和圆心角的关系.
我们猜测也相等
A
B
C
D
E
讲授新课
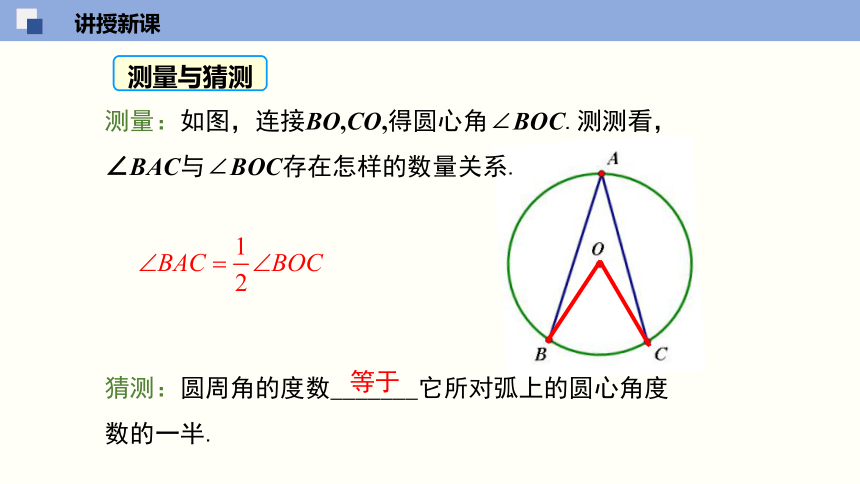
测量:如图,连接BO,CO,得圆心角∠BOC.测测看,∠BAC与∠BOC存在怎样的数量关系.
测量与猜测
猜测:圆周角的度数_______它所对弧上的圆心角度数的一半.
等于
讲授新课
问题 变动点A的位置,看看上述结论是否依然成立?
A
A
A
变动点A的位置,圆周角的度数没有变化,它的度数恰好为同弧所对的圆心角的度数的一半.
讲授新课
圆心O在∠BAC的内部
圆心O在
∠BAC的一边上
圆心O在
∠BAC的外部
圆心O与圆周角的位置有以下三种情况,我们一一讨论.
讲授新课
与同桌或邻近桌的同学交流,猜测一条弧所对的圆周角
与圆心角有什么关系.你能证明这个猜测吗?
·
A
O
C
B
情形一 圆周角的一边通过圆心.
如图 圆O中,∠BAC的一边AB通过圆心.
从而∠BOC=∠C+∠BAC
=2∠BAC,
由于OA=OC,因此∠C=∠BAC,
即∠BAC= ∠BOC
∠BAC= ∠BOC
讲授新课
·
D
A
O
C
B
情形二 圆心在圆心角的内部
如图,圆O在∠BAC的内部.作直径AD,
根据情形一的结果得
∠BAD = —————,
∠DAC = —————.
= ——————
从而∠BAC=∠BAD+∠DAC
= ——————
讲授新课
情形三 圆心在圆周角的外部.
A
·
O
B
C
D
一条弧所对的圆周角等于它所对的圆心角的一半.
综上所述,我们证明了下述定理:
你能证明∠BAC= ∠BOC吗?
如图,圆心O在∠BAC的外部.
证明:
∵∠BAD= ∠BOD
∠CAD= ∠COD
∴∠BAD-CAD= (∠BOD-∠COD)
∴∠BAC= ∠BOC
作直径AD
讲授新课
圆周角定理:
圆周角的度数等于它所对弧上的圆心角度数的一半.
圆周角定理及其推论
A1
A2
A3
推论1:
同弧所对的圆周角相等.
要点归纳
典型例题
B
C
O
.
70°
A
例题2、如图OA,OB,OC都是⊙O的半径,已知∠AOB=50°
∠BOC=70°求∠ACB和∠BAC度数.
∴∠ACB= ∠AOB=25°
同理∠BAC= ∠BOC=35°
解:∵圆心角∠AOB 与圆周角∠ACB
所对的弧为 弧AB
练一练
1.如图,AB是⊙O的直径,C是⊙O上的点,已知∠AOC=45°,则∠B=_______, ∠A=_________; ∠ACB=_______
B
A
C
O.
22.5°
67.5°
90°
讲授新课
2、如图,点A、B、C是圆O上的三点,且四边形ABCO是平行四边形,OF⊥OC交圆O于点F,则∠BAF等于( )
A.12.5° B.15°
C.20° D.22.5°
练一练
解析:连接OB,
∵四边形ABCO是平行四边形,
∴OC=AB,又OA=OB=OC,
∴OA=OB=AB,
∴△AOB为等边三角形,
∵OF⊥OC,OC∥AB,
∴OF⊥AB,
∴∠BOF=∠AOF=30°,
由圆周角定理得∠BAF= ∠BOF=15°,
故选:B.
当堂检测
答:(1)、(2)是圆周角,(3)、(4)不是圆周角,
因(3)、(4)不满足圆周角定义,角顶点没在圆上.
1.下图中各角是不是圆周角?请说明理由.
(1)
(2)
(3)
(4)
当堂检测
解:∵点A、B、C、D在
⊙O上,∠BAC=35°,
2、如图,点A、B、C、D在⊙O上,∠BAC=35°.求∠BDC、∠BOC的度数.
∴∠BDC=∠BAC=35°.
(同弧所对圆周角相等)
∴∠BOC=2∠BAC=70°.
(同弧所对的圆周角等
于圆心角的一半)
当堂检测
3. 如图,在圆O中,弦AB与CD相交于点M. 若∠CAB = 25°, ∠ABD=95°, 试求∠CDB 和∠ACD 的度数.
圆周角∠ACD与圆周角∠ABD所对的
弧均为 ,
∵
解:
∠ACD= ∠ABD= 95°.
∴
同理 ∠CDB = ∠CAB= 25°.
当堂检测
4. 如图, 点A,B,C 在⊙O 上, AC∥OB. 若∠OBA=25°, 求∠BOC的度数.
圆周角∠BAC与圆心角∠BOC所对的
弧均为 ,
∵
∠BOC = 2∠BAC = 50°.
∴
解
∵ AC∥OB,∠OBA=25°,
∠BAC= ∠OBA=25°.
∴
当堂检测
5. 如图, 在⊙O 中,AB是直径, C,D是圆上两点,
且AC =AD.
求证:BC=BD.
∵ AC=AD,
∴ ∠AOC=∠AOD.
∴ ∠COB=∠DOB.
∴ BC=BD.
证明
连接CO、DO.
当堂检测
C
6、如图,对于圆心O在圆周角∠APB外部的情形,证明∠APB= ∠AOB.
证明:连接PO并延长交⊙O于点C.
易知PO=BO=CO,
∴ ∠OAP=∠OPA,∠OBP=∠OPB.
由外角和定理易知
∠COA=∠OAP+∠OPA=2∠OPA;
∠COB=∠OBP+∠OPB=2∠OPB.
而∠AOB=∠COB-∠COA=2∠OPB-2∠OPA=2∠APB.
∴ ∠APB= ∠AOB.
当堂检测
7、如图,∠ACB与∠ADB分别为⊙O上同一条弧AB所对的两个圆周角.
(1) ∠ACB与∠ADB之间具有怎样的大小关系?把你猜想和大家进行交流.
(2)试证明你的猜想.
(1) ∠ACB=∠ADB
(2)连接AO,BO,CO,DO.由同弧所对的圆周角等于所对的圆心角的一半可知:
∠AOB=2∠ADB=2∠ACB.所以∠ACB=∠ADB.
解:
课堂小结
一 、这节课主要学习了两个知识点:
1、圆周角定义.
2、圆周角定理及其定理应用.
二、方法上主要学习了圆周角定理的证明渗透了“特殊到一般”的思想方法和分类讨论的思想方法.
三、圆周角及圆周角定理的应用极其广泛,也是中考的一个重要考点,望同学们灵活运用.
课堂小结
圆心角
类比
圆周角
圆周角定义
圆周角定理
圆周角定理的推论1
圆周角的度数等于它所对弧上的圆心角度数的一半.
同弧或等弧所对的圆周角相等;
1.顶点在圆上,2.两边都与圆相交的角
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
苏科版 九年级上册
2.4 圆周角
第1课时 圆周角与圆心角的关系
学习目标
1.结合图形了解圆心角、圆周角的概念和区别;会叙述并且证明圆周角定理;
2.利用圆心角与圆周角的关系解决与圆相关的几何问题;
3.熟练掌握圆周角定理的推论,并学会其证明过程与应用;
当堂检测
知识回顾
1.什么叫圆心角
.
O
A
B
顶点在圆心的角叫圆心角
2. 圆心角、弧、弦三个量之间关系的一个结论,这个结论是什么?
在同圆(或等圆)中,如果圆心角、弧、弦有一组量相等,那么它们所对应的其余两个量都分别相等.
导入新课
在射门过程中,球员射中球门的难易与它所处的位置B对球门AC的张角( ∠ABC )有关.
A
B
C
D
E
导入新课
各抒己见:图中的∠ABC、∠ADC和∠AEC的顶点各在圆的什么位置?它们的两边和圆是什么关系?
顶点在☉O上,角的两边分别与☉O相交.
再思考一下:∠ABC、∠ADC和∠AEC的度数有什么关系呢?
讲授新课
知识点一 圆周角的概念
顶点在圆上,并且两边都与圆相交的角叫作圆周角.(如∠BAC)
注:两个条件,缺一不可!
我们把∠BAC叫作BC所对圆周角,BC叫作圆周角∠BAC所对的弧.
⌒
⌒
讲授新课
圆周角在我们生活中处处可见,比如,我们从团旗上的图案抽象出如图所示图形,图形中就有很多圆周角.
E
·
A
O
D
B
C
典型例题
例题1:判别下列各图形中的角是不是圆周角,并说明理由.
不是
不是
是
不是
不是
图1
图2
图3
图4
图5
练一练
·
C
O
A
B
·
C
O
B
·
C
O
B
A
A
·
C
O
A
B
·
C
O
B
·
C
O
B
A
A
判一判:下列各图中的∠BAC是否为圆周角,并简述理由.
(2)
(1)
(3)
(5)
(6)
顶点不在圆上
顶点不在圆上
边AC没有和圆相交
√
√
√
讲授新课
知识点二 圆周角定理及其推论
图中的∠ABC、∠ADC和∠AEC都是AC所对的圆周角,我们知道在同圆或等圆中,相等的弧所对的圆心角相等,那么图中的三个圆周角有什么关系?
⌒
A
B
C
D
E
讲授新课
为了弄清楚这三个角的关系,我们先来研究一条弧所对的圆周角和圆心角的关系.
我们猜测也相等
A
B
C
D
E
讲授新课
测量:如图,连接BO,CO,得圆心角∠BOC.测测看,∠BAC与∠BOC存在怎样的数量关系.
测量与猜测
猜测:圆周角的度数_______它所对弧上的圆心角度数的一半.
等于
讲授新课
问题 变动点A的位置,看看上述结论是否依然成立?
A
A
A
变动点A的位置,圆周角的度数没有变化,它的度数恰好为同弧所对的圆心角的度数的一半.
讲授新课
圆心O在∠BAC的内部
圆心O在
∠BAC的一边上
圆心O在
∠BAC的外部
圆心O与圆周角的位置有以下三种情况,我们一一讨论.
讲授新课
与同桌或邻近桌的同学交流,猜测一条弧所对的圆周角
与圆心角有什么关系.你能证明这个猜测吗?
·
A
O
C
B
情形一 圆周角的一边通过圆心.
如图 圆O中,∠BAC的一边AB通过圆心.
从而∠BOC=∠C+∠BAC
=2∠BAC,
由于OA=OC,因此∠C=∠BAC,
即∠BAC= ∠BOC
∠BAC= ∠BOC
讲授新课
·
D
A
O
C
B
情形二 圆心在圆心角的内部
如图,圆O在∠BAC的内部.作直径AD,
根据情形一的结果得
∠BAD = —————,
∠DAC = —————.
= ——————
从而∠BAC=∠BAD+∠DAC
= ——————
讲授新课
情形三 圆心在圆周角的外部.
A
·
O
B
C
D
一条弧所对的圆周角等于它所对的圆心角的一半.
综上所述,我们证明了下述定理:
你能证明∠BAC= ∠BOC吗?
如图,圆心O在∠BAC的外部.
证明:
∵∠BAD= ∠BOD
∠CAD= ∠COD
∴∠BAD-CAD= (∠BOD-∠COD)
∴∠BAC= ∠BOC
作直径AD
讲授新课
圆周角定理:
圆周角的度数等于它所对弧上的圆心角度数的一半.
圆周角定理及其推论
A1
A2
A3
推论1:
同弧所对的圆周角相等.
要点归纳
典型例题
B
C
O
.
70°
A
例题2、如图OA,OB,OC都是⊙O的半径,已知∠AOB=50°
∠BOC=70°求∠ACB和∠BAC度数.
∴∠ACB= ∠AOB=25°
同理∠BAC= ∠BOC=35°
解:∵圆心角∠AOB 与圆周角∠ACB
所对的弧为 弧AB
练一练
1.如图,AB是⊙O的直径,C是⊙O上的点,已知∠AOC=45°,则∠B=_______, ∠A=_________; ∠ACB=_______
B
A
C
O.
22.5°
67.5°
90°
讲授新课
2、如图,点A、B、C是圆O上的三点,且四边形ABCO是平行四边形,OF⊥OC交圆O于点F,则∠BAF等于( )
A.12.5° B.15°
C.20° D.22.5°
练一练
解析:连接OB,
∵四边形ABCO是平行四边形,
∴OC=AB,又OA=OB=OC,
∴OA=OB=AB,
∴△AOB为等边三角形,
∵OF⊥OC,OC∥AB,
∴OF⊥AB,
∴∠BOF=∠AOF=30°,
由圆周角定理得∠BAF= ∠BOF=15°,
故选:B.
当堂检测
答:(1)、(2)是圆周角,(3)、(4)不是圆周角,
因(3)、(4)不满足圆周角定义,角顶点没在圆上.
1.下图中各角是不是圆周角?请说明理由.
(1)
(2)
(3)
(4)
当堂检测
解:∵点A、B、C、D在
⊙O上,∠BAC=35°,
2、如图,点A、B、C、D在⊙O上,∠BAC=35°.求∠BDC、∠BOC的度数.
∴∠BDC=∠BAC=35°.
(同弧所对圆周角相等)
∴∠BOC=2∠BAC=70°.
(同弧所对的圆周角等
于圆心角的一半)
当堂检测
3. 如图,在圆O中,弦AB与CD相交于点M. 若∠CAB = 25°, ∠ABD=95°, 试求∠CDB 和∠ACD 的度数.
圆周角∠ACD与圆周角∠ABD所对的
弧均为 ,
∵
解:
∠ACD= ∠ABD= 95°.
∴
同理 ∠CDB = ∠CAB= 25°.
当堂检测
4. 如图, 点A,B,C 在⊙O 上, AC∥OB. 若∠OBA=25°, 求∠BOC的度数.
圆周角∠BAC与圆心角∠BOC所对的
弧均为 ,
∵
∠BOC = 2∠BAC = 50°.
∴
解
∵ AC∥OB,∠OBA=25°,
∠BAC= ∠OBA=25°.
∴
当堂检测
5. 如图, 在⊙O 中,AB是直径, C,D是圆上两点,
且AC =AD.
求证:BC=BD.
∵ AC=AD,
∴ ∠AOC=∠AOD.
∴ ∠COB=∠DOB.
∴ BC=BD.
证明
连接CO、DO.
当堂检测
C
6、如图,对于圆心O在圆周角∠APB外部的情形,证明∠APB= ∠AOB.
证明:连接PO并延长交⊙O于点C.
易知PO=BO=CO,
∴ ∠OAP=∠OPA,∠OBP=∠OPB.
由外角和定理易知
∠COA=∠OAP+∠OPA=2∠OPA;
∠COB=∠OBP+∠OPB=2∠OPB.
而∠AOB=∠COB-∠COA=2∠OPB-2∠OPA=2∠APB.
∴ ∠APB= ∠AOB.
当堂检测
7、如图,∠ACB与∠ADB分别为⊙O上同一条弧AB所对的两个圆周角.
(1) ∠ACB与∠ADB之间具有怎样的大小关系?把你猜想和大家进行交流.
(2)试证明你的猜想.
(1) ∠ACB=∠ADB
(2)连接AO,BO,CO,DO.由同弧所对的圆周角等于所对的圆心角的一半可知:
∠AOB=2∠ADB=2∠ACB.所以∠ACB=∠ADB.
解:
课堂小结
一 、这节课主要学习了两个知识点:
1、圆周角定义.
2、圆周角定理及其定理应用.
二、方法上主要学习了圆周角定理的证明渗透了“特殊到一般”的思想方法和分类讨论的思想方法.
三、圆周角及圆周角定理的应用极其广泛,也是中考的一个重要考点,望同学们灵活运用.
课堂小结
圆心角
类比
圆周角
圆周角定义
圆周角定理
圆周角定理的推论1
圆周角的度数等于它所对弧上的圆心角度数的一半.
同弧或等弧所对的圆周角相等;
1.顶点在圆上,2.两边都与圆相交的角
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
