3.3圆周角(2)课件(共25张PPT)
文档属性
| 名称 | 3.3圆周角(2)课件(共25张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 260.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-19 15:22:05 | ||
图片预览




文档简介
(共25张PPT)
青岛版 数学 九(上) 第3章: 对圆的进一步认识
3.3 圆周角 (2)
复习回顾
1、什么叫做圆周角
一条弧所对的圆周角等于它所对的圆心角的一半.
2、圆周角定理:
3、圆周角定理的推论1:
圆周角的度数等于它所对弧的度数的一半.
定义(1):顶点在圆上,且角的两边分别与圆相交的角
叫做圆周角.
定义(2):两条有公共端点的弦所夹的角叫做圆周角.
新知探索一
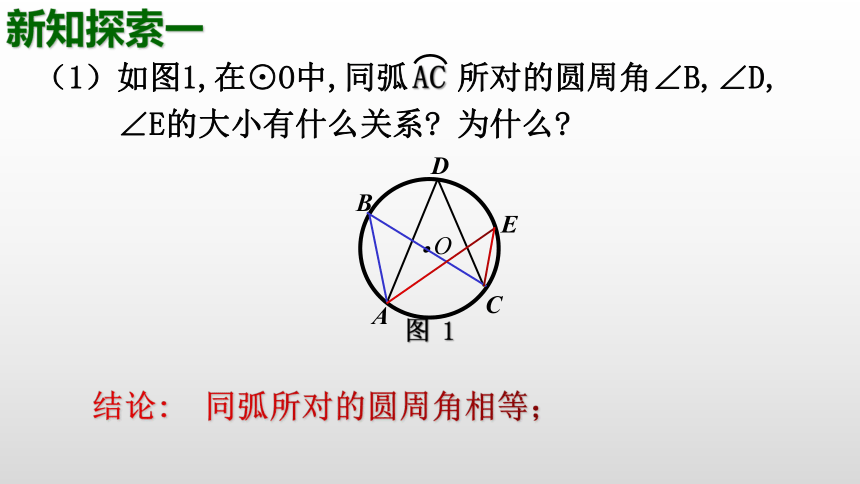
(1)如图1,在⊙O中,同弧 所对的圆周角∠B,∠D,
∠E的大小有什么关系 为什么
AC
● O
B
A
C
D
E
图 1
结论: 同弧所对的圆周角相等;
AC =
EF
(2)如图2,在⊙O中,若 那么圆周角∠B,∠D
的大小有什么关系 为什么
● O
B
A
C
D
E
F
图 2
新知探索一
AC与
EF
(3)如图2,在⊙O中,若圆周角∠B=∠D,那么 是
等弧吗 为什么
结论:
(1) 等弧所对的圆周角相等;
(2)同圆中,相等的圆周角所对的弧也相等。
AC =
EF
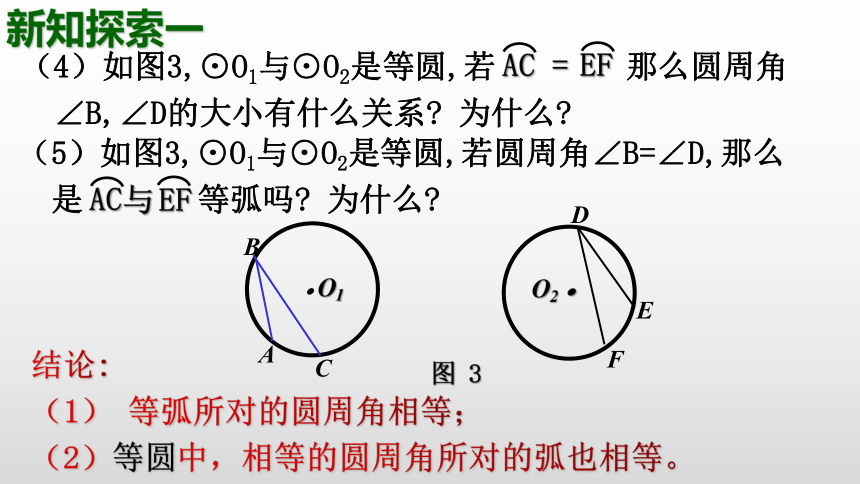
(4)如图3,⊙O1与⊙O2是等圆,若 那么圆周角
∠B,∠D的大小有什么关系 为什么
新知探索一
AC与
EF
(5)如图3,⊙O1与⊙O2是等圆,若圆周角∠B=∠D,那么
是 等弧吗 为什么
结论:
(1) 等弧所对的圆周角相等;
(2)等圆中,相等的圆周角所对的弧也相等。
● O1
B
A
C
图 3
O2 ●
D
E
F
新授知识小结1
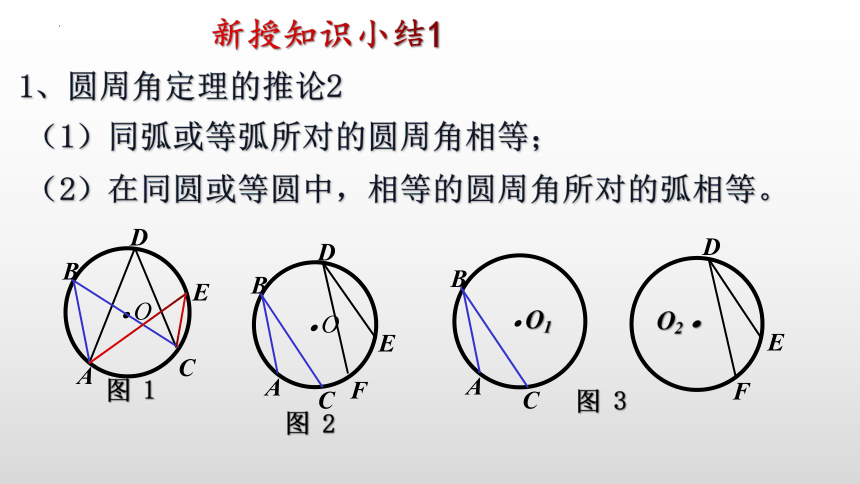
1、圆周角定理的推论2
(1)同弧或等弧所对的圆周角相等;
(2)在同圆或等圆中,相等的圆周角所对的弧相等。
● O
B
A
C
D
E
图 1
● O
B
A
C
D
E
F
图 2
● O1
B
A
C
图 3
O2 ●
D
E
F
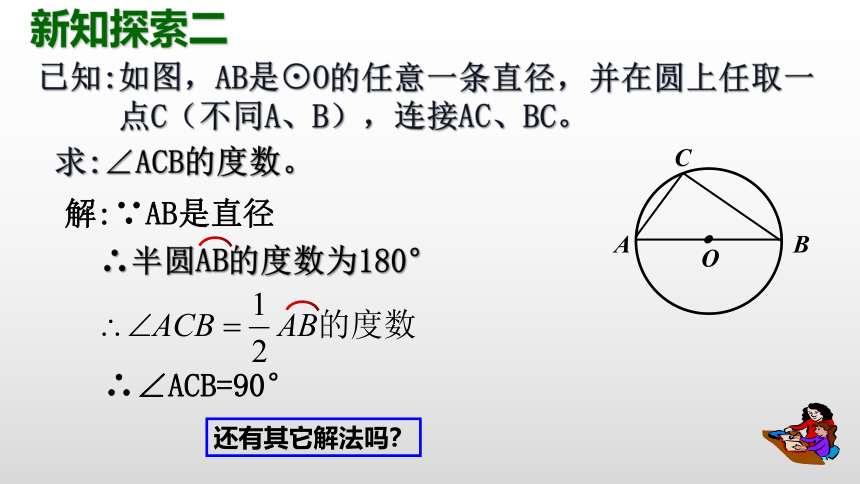
求:∠ACB的度数。
已知:如图,AB是⊙O的任意一条直径,并在圆上任取一
点C(不同A、B),连接AC、BC。
●O
C
A
B
新知探索二
解:∵AB是直径
∴半圆AB的度数为180°
∴∠ACB=90°
还有其它解法吗?
A
C
O
B
图1
1
2
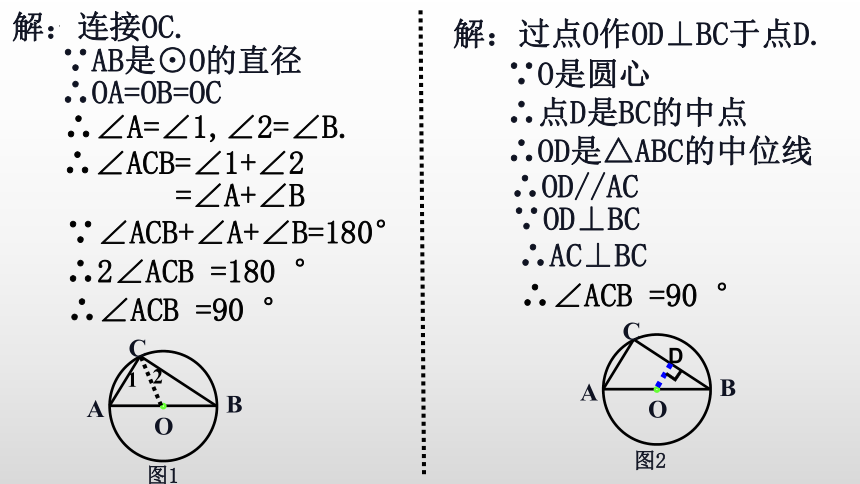
解:连接OC.
∴∠A=∠1,∠2=∠B.
∴∠ACB=∠1+∠2
=∠A+∠B
∵∠ACB+∠A+∠B=180°
∴2∠ACB =180 °
∴∠ACB =90 °
A
C
O
B
图2
解:过点O作OD⊥BC于点D.
D
┓
∵AB是⊙O的直径
∴OA=OB=OC
∵O是圆心
∴点D是BC的中点
∴OD是△ABC的中位线
∴OD//AC
∵OD⊥BC
∴AC⊥BC
∴∠ACB =90 °
2、圆周角定理的推论3:
(1)半圆(或直径)所对的圆周角是直角.
新授知识小结2
你能说出该定理的逆命题吗?
这个逆命题是真命题吗?
(2)90°的圆周角所对的弦是直径.
你能证明该逆定理吗?
已知:A,B,C是⊙O上任一点,∠ACB =90°
求证:AB是⊙O的直径.
证明:取AB的中点O,并连接OC.
∵△ABC是直角三角形,
点O是 AB的中点,
∴OA=OB=OC
∴O是△ABC的外接圆圆心
∵AB是△ABC外接圆的弦,并且过圆心O
∴弦AB是圆的直径
A
B
C
●O
例题讲解
例1、如图,△ABC内接与⊙O,A为劣弧 的中点,∠BAC=
120°,过点B作⊙O的直径BD,连接AD,若AD=6,求AC的长.
BC
A
C
O
B
D
解:点A是劣弧BC的中点
∴AB=
AC
∴∠ABC=∠ACB
∵∠BAC=120°
∴∠ACB=120°
∴∠D=∠ACB=120°
∵BD是⊙O的直径
∴∠DAB=90°
在Rt△ABD中
∵AD=6
例2、如图,AB是⊙O的直径,D是圆上任意一点(不与A、B重合),连接BD并延长到C,使BD=DC,连接AC。
试判断△ABC的形状。
C
D
●O
B
A
温馨提示:
(1)有直径时,常常添加辅助线,构造直径所对的圆周角。
例题讲解
(2)有两个中点时,常常构造三角形的中位线。
C
D
●O
B
A
C
D
●O
B
A
理由:连接AD
∴AB是⊙O的直径
∴∠ADB=90°
∴AD⊥BC
∵BD=CD
∴AD是BC的垂直平分线
∴AB=AC
解:△ABC是等腰三角形
∴△ABC是等腰三角形
解:△ABC是等腰三角形
理由:连接OD
∴OB=OD
∴∠OBD=∠ODB
∵O是AB的中点,BD=CD
∴OD是△ABC的中位线
∴OD//AC
∴∠C=∠ODB
∴∠OBD=∠C
∴△ABC是等腰三角形
A
B
C
m
D
O●
例3、如图,已知:△ABC内接于⊙O,AC=5,BC=12,AB=13,
D是AmB的中点。
求:BD的长。
例题讲解
提示:①△ABC是直角三角形吗?
②弦AB是直径吗?
③怎样把弦BD转化到直角三角形中?
解:连接AD
∵AC=5,BC=12,AB=13
∴AC2+BC2=AB2
∴∠ACB=90°
∴AB是⊙O的直径
∴∠ADB=90°
∵点D是 的中点
AmB
AD
BD
∴ =
∴ AD=BD
∴∠DBA=∠DAB=45°
A
B
C
m
D
O●
在Rt△ABD中
例4、如图,AD是△ABC的高,AE是△ABC的外接圆直径。
求证:AB·AC = AE·AD
提示:
① AB·AC = AE·AD由什么式子变形得到?
△ABD∽△AEC或△ABE∽△ADC
例题讲解
A
O
B
C
D
E
┓
③若得到两三角形相似,得作什么辅助线呢?
A
O
B
C
D
E
┓
证明:连接CE
∵AE是⊙O的直径
∴∠ACE=90°
∴∠ADB=90°
∵AD⊥BC
∴∠ADB=∠ACE
∵∠ABD=∠AEC
(同弧所对的圆周角相等)
∴△ABD∽△AEC
∴AB·AC = AE·AD
A
O
B
C
D
E
┓
证明:连接BE
∵AE是⊙O的直径
∴∠ABE=90°
∴∠ADC=90°
∵AD⊥BC
∴∠ABE=∠ADC
∵∠AEB=∠ACD
(同弧所对的圆周角相等)
∴△ABE∽△ADC
∴AB·AC = AE·AD
例题讲解
A
O
B
C
D
E
┓
F
例5、如图,AB是⊙O的直径,E为⊙O上一点,C是AE的中点,
CD⊥AB垂足为D,AE交CD于F,连接AC。
求证:AF=CF.
提示:
① 因为AF,CF是△ACF的两边,若
证AF=CF,得证哪两个角相等?
∠FAC=∠FCA
②∠FAC是圆周角,它所对的弧是CE,
而AC所对的圆周角是哪一个呢?
③怎样添加辅助线?
④又怎样证∠ABC=∠FCA
A
O
B
C
D
E
┓
F
证明:连接BC
∵AB是⊙O的直径
∴∠ACB=90°
∴∠ADC=90°
∵CD⊥AB
∴∠FCA=∠ABC
∴∠ABC+∠DAC=90°
∴∠FCA+∠DAC=90°
∴AC=
CE
∵C是AE的中点
∴∠FAC=∠ABC
∴∠FCA=∠FAC
∴AF=CF
练 习
P87 练习 第1、2题
3、如图,已知:OA是⊙O的半径,以OA为直径的⊙C与⊙O的弦AB相交于点D。
求:AD与BD的关系,并说明理由。
A
●O
●
C
D
B
温馨提示:有直径时,常常添加辅助线,构造直径所对的圆周角。
练 习
AD=BD
课堂小结
1、圆周角定理的推论2:
(1)同弧或等弧所对的圆周角相等;
(2)在同圆或等圆中,相等的圆周角所对的弧相等。
2、圆周角定理的推论3:
(1)半圆(或直径)所对的圆周角是直角.
(2)90°的圆周角所对的弦是直径.
P89-90习题3.3 第4、5、7题
作 业
结束寄语
不学自知,不问自晓,
古今行事,未之有也.
再见
青岛版 数学 九(上) 第3章: 对圆的进一步认识
3.3 圆周角 (2)
复习回顾
1、什么叫做圆周角
一条弧所对的圆周角等于它所对的圆心角的一半.
2、圆周角定理:
3、圆周角定理的推论1:
圆周角的度数等于它所对弧的度数的一半.
定义(1):顶点在圆上,且角的两边分别与圆相交的角
叫做圆周角.
定义(2):两条有公共端点的弦所夹的角叫做圆周角.
新知探索一
(1)如图1,在⊙O中,同弧 所对的圆周角∠B,∠D,
∠E的大小有什么关系 为什么
AC
● O
B
A
C
D
E
图 1
结论: 同弧所对的圆周角相等;
AC =
EF
(2)如图2,在⊙O中,若 那么圆周角∠B,∠D
的大小有什么关系 为什么
● O
B
A
C
D
E
F
图 2
新知探索一
AC与
EF
(3)如图2,在⊙O中,若圆周角∠B=∠D,那么 是
等弧吗 为什么
结论:
(1) 等弧所对的圆周角相等;
(2)同圆中,相等的圆周角所对的弧也相等。
AC =
EF
(4)如图3,⊙O1与⊙O2是等圆,若 那么圆周角
∠B,∠D的大小有什么关系 为什么
新知探索一
AC与
EF
(5)如图3,⊙O1与⊙O2是等圆,若圆周角∠B=∠D,那么
是 等弧吗 为什么
结论:
(1) 等弧所对的圆周角相等;
(2)等圆中,相等的圆周角所对的弧也相等。
● O1
B
A
C
图 3
O2 ●
D
E
F
新授知识小结1
1、圆周角定理的推论2
(1)同弧或等弧所对的圆周角相等;
(2)在同圆或等圆中,相等的圆周角所对的弧相等。
● O
B
A
C
D
E
图 1
● O
B
A
C
D
E
F
图 2
● O1
B
A
C
图 3
O2 ●
D
E
F
求:∠ACB的度数。
已知:如图,AB是⊙O的任意一条直径,并在圆上任取一
点C(不同A、B),连接AC、BC。
●O
C
A
B
新知探索二
解:∵AB是直径
∴半圆AB的度数为180°
∴∠ACB=90°
还有其它解法吗?
A
C
O
B
图1
1
2
解:连接OC.
∴∠A=∠1,∠2=∠B.
∴∠ACB=∠1+∠2
=∠A+∠B
∵∠ACB+∠A+∠B=180°
∴2∠ACB =180 °
∴∠ACB =90 °
A
C
O
B
图2
解:过点O作OD⊥BC于点D.
D
┓
∵AB是⊙O的直径
∴OA=OB=OC
∵O是圆心
∴点D是BC的中点
∴OD是△ABC的中位线
∴OD//AC
∵OD⊥BC
∴AC⊥BC
∴∠ACB =90 °
2、圆周角定理的推论3:
(1)半圆(或直径)所对的圆周角是直角.
新授知识小结2
你能说出该定理的逆命题吗?
这个逆命题是真命题吗?
(2)90°的圆周角所对的弦是直径.
你能证明该逆定理吗?
已知:A,B,C是⊙O上任一点,∠ACB =90°
求证:AB是⊙O的直径.
证明:取AB的中点O,并连接OC.
∵△ABC是直角三角形,
点O是 AB的中点,
∴OA=OB=OC
∴O是△ABC的外接圆圆心
∵AB是△ABC外接圆的弦,并且过圆心O
∴弦AB是圆的直径
A
B
C
●O
例题讲解
例1、如图,△ABC内接与⊙O,A为劣弧 的中点,∠BAC=
120°,过点B作⊙O的直径BD,连接AD,若AD=6,求AC的长.
BC
A
C
O
B
D
解:点A是劣弧BC的中点
∴AB=
AC
∴∠ABC=∠ACB
∵∠BAC=120°
∴∠ACB=120°
∴∠D=∠ACB=120°
∵BD是⊙O的直径
∴∠DAB=90°
在Rt△ABD中
∵AD=6
例2、如图,AB是⊙O的直径,D是圆上任意一点(不与A、B重合),连接BD并延长到C,使BD=DC,连接AC。
试判断△ABC的形状。
C
D
●O
B
A
温馨提示:
(1)有直径时,常常添加辅助线,构造直径所对的圆周角。
例题讲解
(2)有两个中点时,常常构造三角形的中位线。
C
D
●O
B
A
C
D
●O
B
A
理由:连接AD
∴AB是⊙O的直径
∴∠ADB=90°
∴AD⊥BC
∵BD=CD
∴AD是BC的垂直平分线
∴AB=AC
解:△ABC是等腰三角形
∴△ABC是等腰三角形
解:△ABC是等腰三角形
理由:连接OD
∴OB=OD
∴∠OBD=∠ODB
∵O是AB的中点,BD=CD
∴OD是△ABC的中位线
∴OD//AC
∴∠C=∠ODB
∴∠OBD=∠C
∴△ABC是等腰三角形
A
B
C
m
D
O●
例3、如图,已知:△ABC内接于⊙O,AC=5,BC=12,AB=13,
D是AmB的中点。
求:BD的长。
例题讲解
提示:①△ABC是直角三角形吗?
②弦AB是直径吗?
③怎样把弦BD转化到直角三角形中?
解:连接AD
∵AC=5,BC=12,AB=13
∴AC2+BC2=AB2
∴∠ACB=90°
∴AB是⊙O的直径
∴∠ADB=90°
∵点D是 的中点
AmB
AD
BD
∴ =
∴ AD=BD
∴∠DBA=∠DAB=45°
A
B
C
m
D
O●
在Rt△ABD中
例4、如图,AD是△ABC的高,AE是△ABC的外接圆直径。
求证:AB·AC = AE·AD
提示:
① AB·AC = AE·AD由什么式子变形得到?
△ABD∽△AEC或△ABE∽△ADC
例题讲解
A
O
B
C
D
E
┓
③若得到两三角形相似,得作什么辅助线呢?
A
O
B
C
D
E
┓
证明:连接CE
∵AE是⊙O的直径
∴∠ACE=90°
∴∠ADB=90°
∵AD⊥BC
∴∠ADB=∠ACE
∵∠ABD=∠AEC
(同弧所对的圆周角相等)
∴△ABD∽△AEC
∴AB·AC = AE·AD
A
O
B
C
D
E
┓
证明:连接BE
∵AE是⊙O的直径
∴∠ABE=90°
∴∠ADC=90°
∵AD⊥BC
∴∠ABE=∠ADC
∵∠AEB=∠ACD
(同弧所对的圆周角相等)
∴△ABE∽△ADC
∴AB·AC = AE·AD
例题讲解
A
O
B
C
D
E
┓
F
例5、如图,AB是⊙O的直径,E为⊙O上一点,C是AE的中点,
CD⊥AB垂足为D,AE交CD于F,连接AC。
求证:AF=CF.
提示:
① 因为AF,CF是△ACF的两边,若
证AF=CF,得证哪两个角相等?
∠FAC=∠FCA
②∠FAC是圆周角,它所对的弧是CE,
而AC所对的圆周角是哪一个呢?
③怎样添加辅助线?
④又怎样证∠ABC=∠FCA
A
O
B
C
D
E
┓
F
证明:连接BC
∵AB是⊙O的直径
∴∠ACB=90°
∴∠ADC=90°
∵CD⊥AB
∴∠FCA=∠ABC
∴∠ABC+∠DAC=90°
∴∠FCA+∠DAC=90°
∴AC=
CE
∵C是AE的中点
∴∠FAC=∠ABC
∴∠FCA=∠FAC
∴AF=CF
练 习
P87 练习 第1、2题
3、如图,已知:OA是⊙O的半径,以OA为直径的⊙C与⊙O的弦AB相交于点D。
求:AD与BD的关系,并说明理由。
A
●O
●
C
D
B
温馨提示:有直径时,常常添加辅助线,构造直径所对的圆周角。
练 习
AD=BD
课堂小结
1、圆周角定理的推论2:
(1)同弧或等弧所对的圆周角相等;
(2)在同圆或等圆中,相等的圆周角所对的弧相等。
2、圆周角定理的推论3:
(1)半圆(或直径)所对的圆周角是直角.
(2)90°的圆周角所对的弦是直径.
P89-90习题3.3 第4、5、7题
作 业
结束寄语
不学自知,不问自晓,
古今行事,未之有也.
再见
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
