人教版七年级上册1.4.2有理数的除法(第一课时)课件(共16张PPT)
文档属性
| 名称 | 人教版七年级上册1.4.2有理数的除法(第一课时)课件(共16张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-21 07:32:48 | ||
图片预览




文档简介
(共16张PPT)
2022/8/20
1.4.2 有理数的除法
第一课时
学习目标
1、理解除法是乘法的逆运算;
2、掌握有理数的除法法则,会进行有理数的除法运算 。
1、说一说有理数的乘法法则:
(1) 9×6
(2) 3×(-4)
(3)(-4)×6
(4) 1×(-6)
(5)(-7)×0
知识回顾
=54
两数相乘,同号得正,异号得负,并把绝对值相乘;
任何数与零相乘都得零。
=-12
=-24
=-6
=0
(6)(-1)×(-6)
(7)
(8)
(9)
(10)
=6
=-1
=1
2、计算:
知识回顾
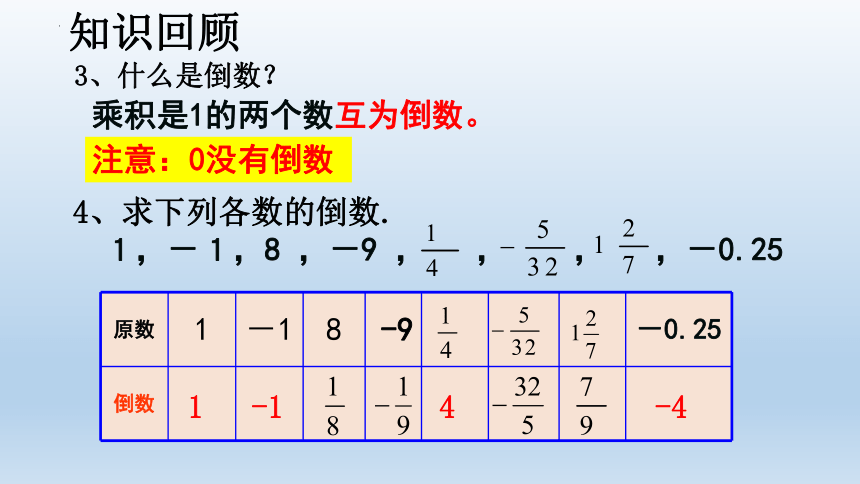
4、求下列各数的倒数.
乘积是1的两个数互为倒数。
3、什么是倒数?
注意:0没有倒数
原数 1 -1 8 -9 -0.25
倒数
1,-1,8 ,-9 , , , ,-0.25
1
-1
4
-4
知识回顾
5、求下列各数的绝对值.
- 1.5, 1.5, - 6, +6,- 3,3, 0.
| -1.5 | =1.5;
解:
正数的绝对值是它本身;
负数的绝对值是它的相反数;
0 的绝对值是 0.
|1.5| =1.5;
|-6| = 6 ;
|+6| = 6 ;
|-3| = 3 ;
|3| = 3 ;
|0| = 0.
(数轴上表示数a的点与原点的距离叫做a的绝对值)
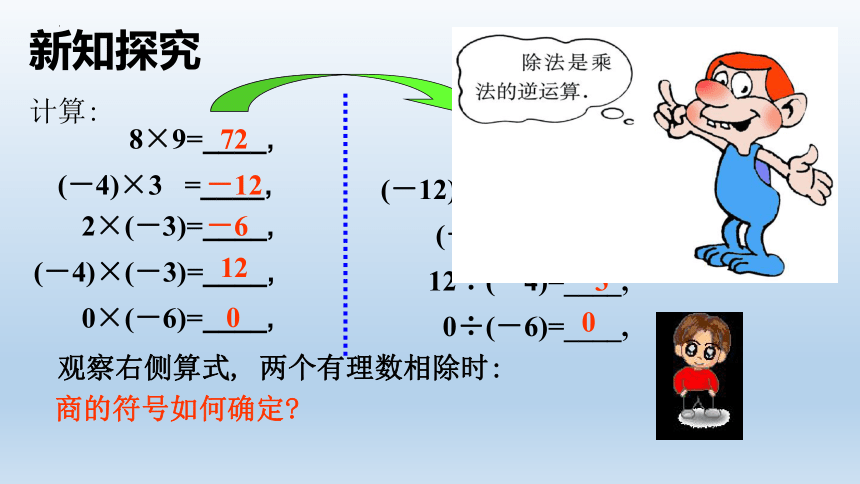
计算:
8×9=____,
(-4)×3 =____,
2×(-3)=____,
(-4)×(-3)=____,
0×(-6)=____,
72
-12
-6
12
0
72÷9=____,
(-12)÷(-4)=____,
(-6) ÷2=____,
12÷(-4)=____,
0÷(-6)=____,
8
3
-3
-3
0
观察右侧算式, 两个有理数相除时:
商的符号如何确定
新知探究
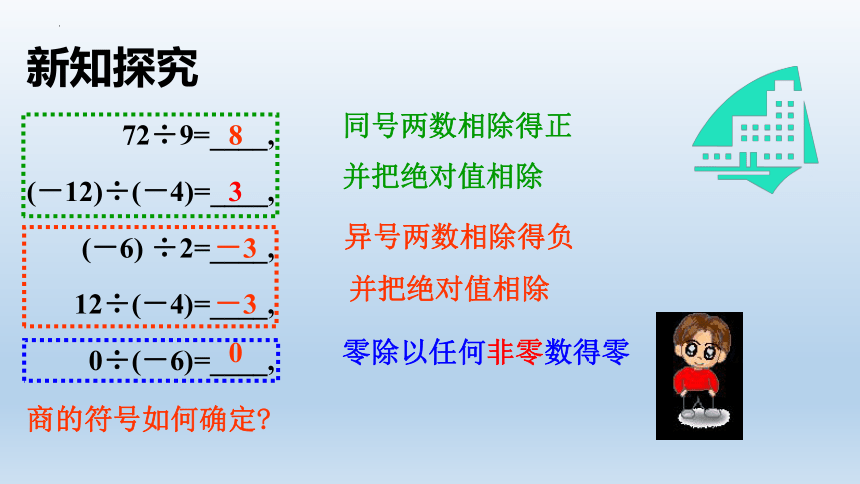
72÷9=____,
(-12)÷(-4)=____,
(-6) ÷2=____,
12÷(-4)=____,
0÷(-6)=____,
8
3
-3
-3
0
商的符号如何确定
同号两数相除得正
并把绝对值相除
异号两数相除得负
并把绝对值相除
零除以任何非零数得零
新知探究
有理数的除法法则:
两个有理数相除, 同号得____,
异号得_____,并把绝对值_______.
0除以任何一个不等于0的数都得___.
正
负
相除
0
注意
0不能作为除数
知识学习
你一定行!
(1) (-8)÷(-4)
(2) (-3.2)÷0.08
解:
(1)原式
=+( )
8÷4
=2
(同号得正,绝对值相除)
(2)原式
=- ( )
3.2÷0.08
=-40
(异号得负,绝对值相除)
(3)原式=
(异号得负,绝对值相除)
求解中的第一步是
_______________ ;
第二步是______________;
确定商的符号
绝对值相除
例题讲解
(3)16÷(-3)
-( )
16 ÷3
=-
知识学习
例
(1)
(2)
解:
(1)原式
= - ( )
(2)原式=
= -( )
= -
除以一个不等于0的数,等于乘这个数的倒数.
=+
=
●
●
●
●
●
除以一个不等于0的数,等于乘这个数的倒数.
也可以表示成:
a ÷ b = a · (b≠0)
除号变乘号
除数变为倒数作因数
归纳总结
有理数的除法法则:
例:计算
解法二:
新知应用
=3
解:原式=(-18)×( )
解:原式=+(18 ÷6)
=3
解:原式= -( )
= -( )
=-3
(3)1 ÷( )
=1×( )
解:原式=1÷( )
解:原式= -( )
= -( )
(2)( )÷0.2
解:原式=( )÷
=-3
化除为乘
运算中遇到小数和分数时,处理的方法与小学一样,小数化成分数,带分数化成假分数,然后相除.
(1) (- 18)÷(- 6)
1、快速抢答
=-4
=+72
=-5
=+32
=0
新知应用
2022/8/20
新知应用
2、计算:
1.有理数除法法则:
两个有理数相除, 同号得正,
异号得负,并把绝对值相除;
0除以任何非0数都得0.
2.除法和乘法之间的关系:
乘法
有理数除法也可以转化为 进行,
其方法是:
除以一个不等于0数, 等于乘这个数的倒数.
归纳小结
再见!
2022/8/20
1.4.2 有理数的除法
第一课时
学习目标
1、理解除法是乘法的逆运算;
2、掌握有理数的除法法则,会进行有理数的除法运算 。
1、说一说有理数的乘法法则:
(1) 9×6
(2) 3×(-4)
(3)(-4)×6
(4) 1×(-6)
(5)(-7)×0
知识回顾
=54
两数相乘,同号得正,异号得负,并把绝对值相乘;
任何数与零相乘都得零。
=-12
=-24
=-6
=0
(6)(-1)×(-6)
(7)
(8)
(9)
(10)
=6
=-1
=1
2、计算:
知识回顾
4、求下列各数的倒数.
乘积是1的两个数互为倒数。
3、什么是倒数?
注意:0没有倒数
原数 1 -1 8 -9 -0.25
倒数
1,-1,8 ,-9 , , , ,-0.25
1
-1
4
-4
知识回顾
5、求下列各数的绝对值.
- 1.5, 1.5, - 6, +6,- 3,3, 0.
| -1.5 | =1.5;
解:
正数的绝对值是它本身;
负数的绝对值是它的相反数;
0 的绝对值是 0.
|1.5| =1.5;
|-6| = 6 ;
|+6| = 6 ;
|-3| = 3 ;
|3| = 3 ;
|0| = 0.
(数轴上表示数a的点与原点的距离叫做a的绝对值)
计算:
8×9=____,
(-4)×3 =____,
2×(-3)=____,
(-4)×(-3)=____,
0×(-6)=____,
72
-12
-6
12
0
72÷9=____,
(-12)÷(-4)=____,
(-6) ÷2=____,
12÷(-4)=____,
0÷(-6)=____,
8
3
-3
-3
0
观察右侧算式, 两个有理数相除时:
商的符号如何确定
新知探究
72÷9=____,
(-12)÷(-4)=____,
(-6) ÷2=____,
12÷(-4)=____,
0÷(-6)=____,
8
3
-3
-3
0
商的符号如何确定
同号两数相除得正
并把绝对值相除
异号两数相除得负
并把绝对值相除
零除以任何非零数得零
新知探究
有理数的除法法则:
两个有理数相除, 同号得____,
异号得_____,并把绝对值_______.
0除以任何一个不等于0的数都得___.
正
负
相除
0
注意
0不能作为除数
知识学习
你一定行!
(1) (-8)÷(-4)
(2) (-3.2)÷0.08
解:
(1)原式
=+( )
8÷4
=2
(同号得正,绝对值相除)
(2)原式
=- ( )
3.2÷0.08
=-40
(异号得负,绝对值相除)
(3)原式=
(异号得负,绝对值相除)
求解中的第一步是
_______________ ;
第二步是______________;
确定商的符号
绝对值相除
例题讲解
(3)16÷(-3)
-( )
16 ÷3
=-
知识学习
例
(1)
(2)
解:
(1)原式
= - ( )
(2)原式=
= -( )
= -
除以一个不等于0的数,等于乘这个数的倒数.
=+
=
●
●
●
●
●
除以一个不等于0的数,等于乘这个数的倒数.
也可以表示成:
a ÷ b = a · (b≠0)
除号变乘号
除数变为倒数作因数
归纳总结
有理数的除法法则:
例:计算
解法二:
新知应用
=3
解:原式=(-18)×( )
解:原式=+(18 ÷6)
=3
解:原式= -( )
= -( )
=-3
(3)1 ÷( )
=1×( )
解:原式=1÷( )
解:原式= -( )
= -( )
(2)( )÷0.2
解:原式=( )÷
=-3
化除为乘
运算中遇到小数和分数时,处理的方法与小学一样,小数化成分数,带分数化成假分数,然后相除.
(1) (- 18)÷(- 6)
1、快速抢答
=-4
=+72
=-5
=+32
=0
新知应用
2022/8/20
新知应用
2、计算:
1.有理数除法法则:
两个有理数相除, 同号得正,
异号得负,并把绝对值相除;
0除以任何非0数都得0.
2.除法和乘法之间的关系:
乘法
有理数除法也可以转化为 进行,
其方法是:
除以一个不等于0数, 等于乘这个数的倒数.
归纳小结
再见!
