1.2.3 相反数 课件 2022-2023学年人教版七年级数学上册 (共16张PPT)
文档属性
| 名称 | 1.2.3 相反数 课件 2022-2023学年人教版七年级数学上册 (共16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-20 21:00:32 | ||
图片预览




文档简介
(共16张PPT)
1.2.3相反数
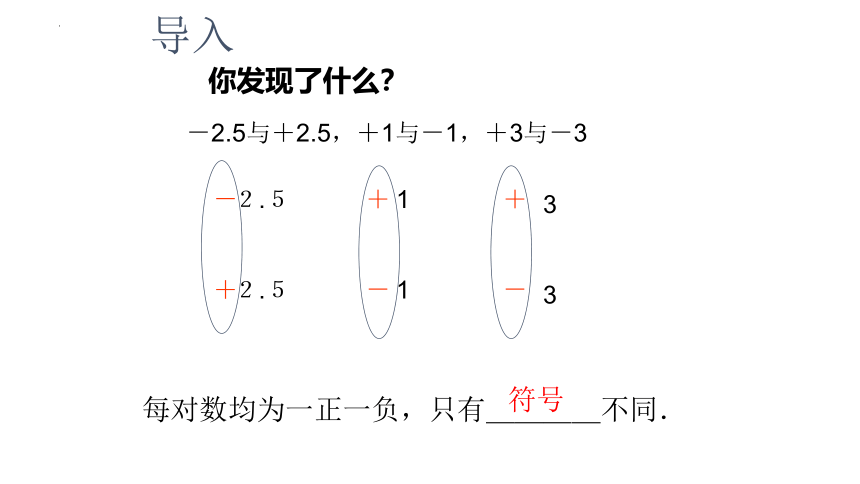
2.5
2.5
1
1
-
+
+
-
+
-
每对数均为一正一负,只有____不同.
符号
3
3
-2.5与+2.5,+1与-1,+3与-3
导入
你发现了什么?
只有符号不同的两个数称互为相反数.
规定: 零的相反数是零 .
结论
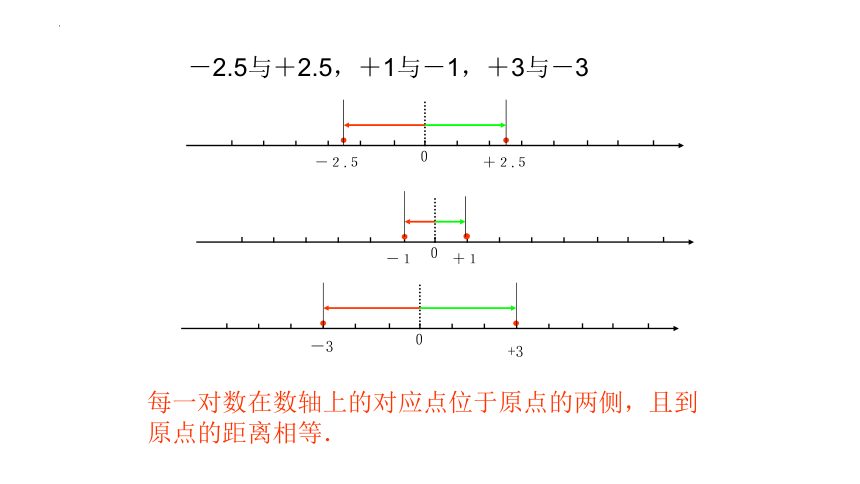
-2.5与+2.5,+1与-1,+3与-3
0
.
.
+2.5
-2.5
0
.
.
+1
-1
0
.
.
每一对数在数轴上的对应点位于原点的两侧,且到原点的距离相等.
-3
+3
我来 辨一辨:
(1)只要符号不同的两个数就称互为相
反数.( )
(2)一个数的相反数一定是负数.( )
(3)零的相反数是零.( )
(4)-8是相反数.( )
×
×
√
×
我来做一做:
(1)分别写出下列各数的相反数:
+11.2, -7, 3 , - ;
(2)指出下列各数是哪个数的相反数:
3.1415926 , -0 , - .
解: (1)+11.2的相反数是-11.2 ,
(2) 3.1415926是- 3.1415926的相反数,
- 是 的相反数.
-7的相反数是+7,
3的相反数是-3,
- 的相反数是+ ;
-0是0的相反数,
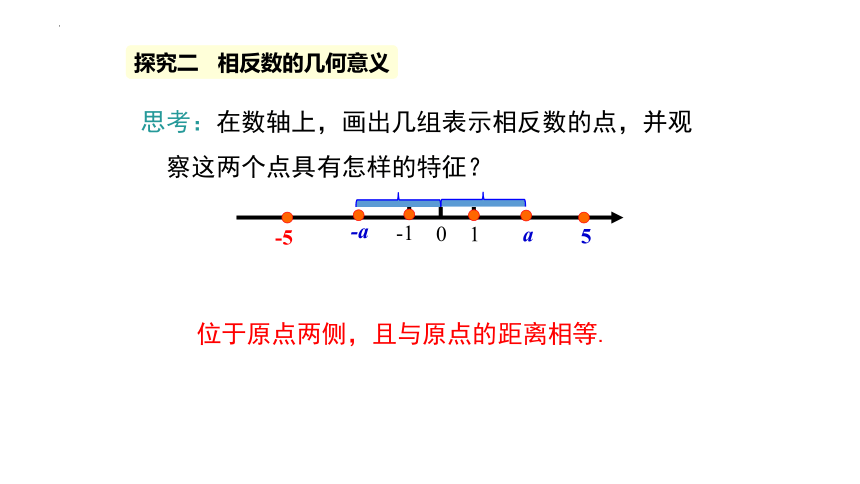
思考:在数轴上,画出几组表示相反数的点,并观
察这两个点具有怎样的特征?
位于原点两侧,且与原点的距离相等.
0
5
-5
-1
1
探究二 相反数的几何意义
a
-a
思考:数轴上到原点的距离相等的点所表示的数有什
么特点?借助数轴填一填:
1.数轴上与原点距离是2的点有____个,这些点表示的
数是________;
2.与原点的距离是5的点有____个,这些点表示的数是
________.
0
2
-2
两
2和-2
5和-5
两
5
-5
1.互为相反数的两个数分别位于原点的两侧(0除外);
2.互为相反数的两个数到原点的距离相等.
要点归纳
几何意义
3.一般地,设a是一个正数,数轴上与原点的距离是
a的点有两个,它们分别在原点的两侧,表示a和
-a,这两点关于原点对称.
1. 在一个数的前面加上一个“ – ”号,表示原来那个数的相反数。
例如:- 7 , + 5的相反数分别是:
- ( -7 )
- ( + 5 )
= 7
= - 5
多重符号的化简
二
(1) 是____的相反数,
(2) 是______的相反数, =______ .
(3) 是_______的相反数, .
(4) 是_______的相反数, .
+4
-4
填一填
思考:如果在一个数前面加上“+”号所得得到的
结果是什么呢?
归纳总结
在一个数前面加上“-”号表示求这个数的相反数.
- 12表示12的相反数。
-(-12)表示什么呢?
-(-12)等于多少?
-[-(-12)]呢?
-{-[+(-12)]}等于多少?
解:- 12
-(-12)表示12的相反数的相反数,所以-(-12)=12
-[-(-12)]=- 12
-{-[+(-12)]}
归纳
具有多重符号的数如何化简?
1、具有多重符号的数的化简过程中,“正号” 可以省略。
2、当“负号” 为奇数个时,结果为负数。
3、当“负号”为偶数个时,结果为正数。
、写出下列各数的
相反数
, -1.5, -12, 0,m, -n
-n一定是负数吗?
1、 当n为正数时,-n表示n的相反数,所以-n为负数。
2、当n为0时,因为0的相反数是0,所以-n等于0.
3、当n为负数时,因为一个负数的相反数是正数,所以-n为正数。
1.2.3相反数
2.5
2.5
1
1
-
+
+
-
+
-
每对数均为一正一负,只有____不同.
符号
3
3
-2.5与+2.5,+1与-1,+3与-3
导入
你发现了什么?
只有符号不同的两个数称互为相反数.
规定: 零的相反数是零 .
结论
-2.5与+2.5,+1与-1,+3与-3
0
.
.
+2.5
-2.5
0
.
.
+1
-1
0
.
.
每一对数在数轴上的对应点位于原点的两侧,且到原点的距离相等.
-3
+3
我来 辨一辨:
(1)只要符号不同的两个数就称互为相
反数.( )
(2)一个数的相反数一定是负数.( )
(3)零的相反数是零.( )
(4)-8是相反数.( )
×
×
√
×
我来做一做:
(1)分别写出下列各数的相反数:
+11.2, -7, 3 , - ;
(2)指出下列各数是哪个数的相反数:
3.1415926 , -0 , - .
解: (1)+11.2的相反数是-11.2 ,
(2) 3.1415926是- 3.1415926的相反数,
- 是 的相反数.
-7的相反数是+7,
3的相反数是-3,
- 的相反数是+ ;
-0是0的相反数,
思考:在数轴上,画出几组表示相反数的点,并观
察这两个点具有怎样的特征?
位于原点两侧,且与原点的距离相等.
0
5
-5
-1
1
探究二 相反数的几何意义
a
-a
思考:数轴上到原点的距离相等的点所表示的数有什
么特点?借助数轴填一填:
1.数轴上与原点距离是2的点有____个,这些点表示的
数是________;
2.与原点的距离是5的点有____个,这些点表示的数是
________.
0
2
-2
两
2和-2
5和-5
两
5
-5
1.互为相反数的两个数分别位于原点的两侧(0除外);
2.互为相反数的两个数到原点的距离相等.
要点归纳
几何意义
3.一般地,设a是一个正数,数轴上与原点的距离是
a的点有两个,它们分别在原点的两侧,表示a和
-a,这两点关于原点对称.
1. 在一个数的前面加上一个“ – ”号,表示原来那个数的相反数。
例如:- 7 , + 5的相反数分别是:
- ( -7 )
- ( + 5 )
= 7
= - 5
多重符号的化简
二
(1) 是____的相反数,
(2) 是______的相反数, =______ .
(3) 是_______的相反数, .
(4) 是_______的相反数, .
+4
-4
填一填
思考:如果在一个数前面加上“+”号所得得到的
结果是什么呢?
归纳总结
在一个数前面加上“-”号表示求这个数的相反数.
- 12表示12的相反数。
-(-12)表示什么呢?
-(-12)等于多少?
-[-(-12)]呢?
-{-[+(-12)]}等于多少?
解:- 12
-(-12)表示12的相反数的相反数,所以-(-12)=12
-[-(-12)]=- 12
-{-[+(-12)]}
归纳
具有多重符号的数如何化简?
1、具有多重符号的数的化简过程中,“正号” 可以省略。
2、当“负号” 为奇数个时,结果为负数。
3、当“负号”为偶数个时,结果为正数。
、写出下列各数的
相反数
, -1.5, -12, 0,m, -n
-n一定是负数吗?
1、 当n为正数时,-n表示n的相反数,所以-n为负数。
2、当n为0时,因为0的相反数是0,所以-n等于0.
3、当n为负数时,因为一个负数的相反数是正数,所以-n为正数。
