2022-2023学年人教版八年级数学上册 11.2.1 三角形的内角 练习(Word版含答案)
文档属性
| 名称 | 2022-2023学年人教版八年级数学上册 11.2.1 三角形的内角 练习(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 308.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-21 09:44:07 | ||
图片预览



文档简介
11.2.1 三角形的内角
一.选择题
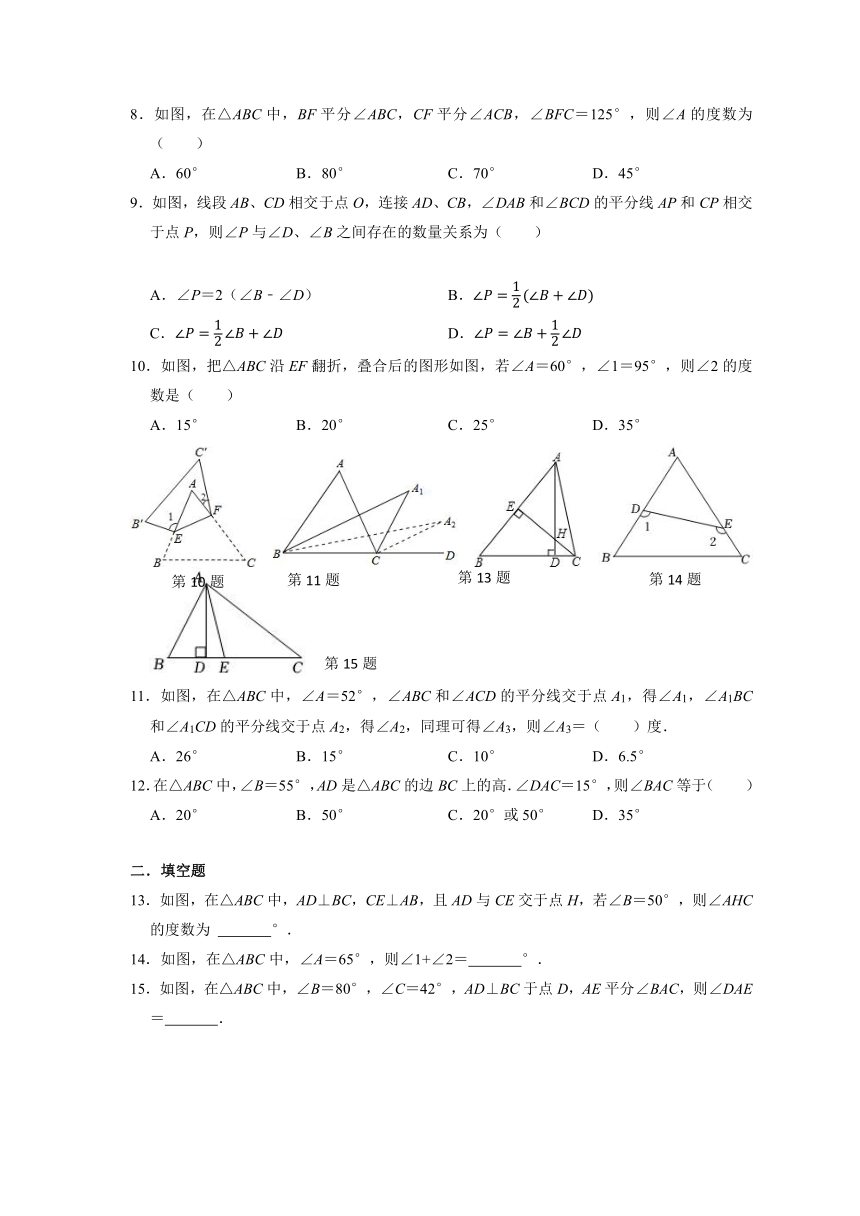
1.如图所示,考古学家发现在地下A处有一座古墓,古墓上方是煤气管道,为了不影响管道,准备在B和C处开工挖出“V”字形通道,如果∠DBA=120°,∠ECA=125°,则∠A的度数是( )
A.65° B.80° C.85° D.90°
2.如图,D是△ABC的BC边上一点,∠B=∠1,∠3=80°,∠BAC=70°.则∠2的大小是( )
A.20° B.25° C.30° D.35°
3.如图,∠B=30°,∠CAD=65°且AD平分∠CAE,则∠ACD等于( )
A.95° B.65° C.50° D.80°
4.如图,在△ABC中,∠A=80°,∠B=36°,将△ABC沿直线BC向右平移到△DEF的位置,则∠F的度数是( )
A.80° B.36° C.64° D.116°
5.如图,在△ABC中,CD是∠ACB的角平分线交AB于点D,DE∥BC,交AC于点E,∠A=60°,∠BDC=80°,则∠EDC的度数为( )
A.10° B.20° C.30° D.40°
6.在一个三角形中,三个内角之比为2:3:5,则这个三角形是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.无法确定
7.如图,在△ABC中,∠ACB=80°,点D在AB上,将△ABC沿CD折叠,点B落在边AC的点E处.若∠ADE=24°,则∠A的度数为( )
A.24° B.32° C.38° D.48°
8.如图,在△ABC中,BF平分∠ABC,CF平分∠ACB,∠BFC=125°,则∠A的度数为( )
A.60° B.80° C.70° D.45°
9.如图,线段AB、CD相交于点O,连接AD、CB,∠DAB和∠BCD的平分线AP和CP相交于点P,则∠P与∠D、∠B之间存在的数量关系为( )
A.∠P=2(∠B﹣∠D) B.
C. D.
10.如图,把△ABC沿EF翻折,叠合后的图形如图,若∠A=60°,∠1=95°,则∠2的度数是( )
A.15° B.20° C.25° D.35°
11.如图,在△ABC中,∠A=52°,∠ABC和∠ACD的平分线交于点A1,得∠A1,∠A1BC和∠A1CD的平分线交于点A2,得∠A2,同理可得∠A3,则∠A3=( )度.
A.26° B.15° C.10° D.6.5°
12.在△ABC中,∠B=55°,AD是△ABC的边BC上的高.∠DAC=15°,则∠BAC等于( )
A.20° B.50° C.20°或50° D.35°
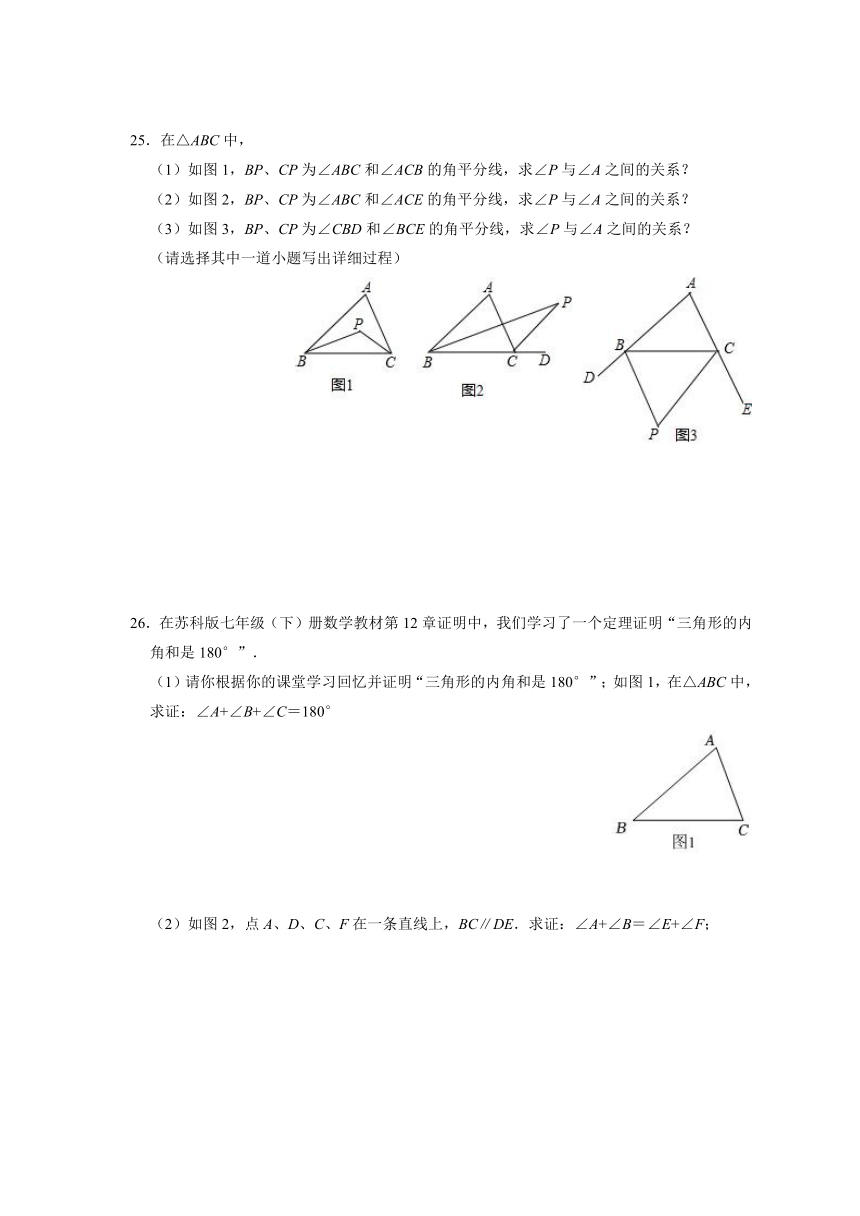
二.填空题
13.如图,在△ABC中,AD⊥BC,CE⊥AB,且AD与CE交于点H,若∠B=50°,则∠AHC的度数为 °.
14.如图,在△ABC中,∠A=65°,则∠1+∠2= °.
15.如图,在△ABC中,∠B=80°,∠C=42°,AD⊥BC于点D,AE平分∠BAC,则∠DAE= .
16.如图,AE,CE分别平分∠BAD和∠BCD,∠B=32°,∠E=35°,则∠D= .
17.如图,直线GD、EH、FI两两相交于点A、B、C,则∠D+∠E+∠F+∠G+∠H+∠I= °.
18.如图,在△ABC中,沿DE折叠,点A落在三角形所在的平面内的点为A′,若∠A=30°,∠BDA′=86°,则∠CEA′的度数为 .
19.如图,∠DBC与∠ECB是△ABC的两个外角,BF平分∠DBC交∠ECB的平分线于点F.若∠F=60°,则∠A= .
20.如图,BA1和CA1分别是△ABC的内角平分线和外角平分线,BA2是∠A1BD的角平分线,CA2是∠A1CD的角平分线,BA3是∠A2BD的角平分线,CA3是∠A2CD的角平分线,若∠A=α,则∠A2022= .
三.解答题
21.如图所示,在△ABC中,AD平分∠BAC交BC于点D,BE平分∠ABC交AD于点E.
(1)若∠C=60°,∠BAC=80°,求∠ADB的度数;
(2)若∠BED=60°,求∠C的度数.
22.如图,在△ABC中,若∠1=∠2,DE∥BC.
(1)试说明FG∥BE;
(2)若BE为∠ABC的角平分线,∠2=30°,∠C=50°,求∠A的度数.
23.如图,在△ABC中,∠B=34°,∠C=70°,AD⊥BC于点D,AE平分∠BAC交BC于点E,DF⊥AE于点F.
(1)求∠BAE的度数;
(2)求∠ADF的度数.
24.(1)如图1,AD平分∠BAC,AE⊥BC,∠B=30°,C=70°,求∠DAE的度数;
(2)如图2,AD平分∠BAC,点F在AD的延长线上,FE⊥BC,∠B=28°,∠C=68°,求∠DFE的度数;
(3)如图3,AD平分∠BAC,EA平分∠BEC,∠C﹣∠B=38°,求∠DAE的度数.
25.在△ABC中,
(1)如图1,BP、CP为∠ABC和∠ACB的角平分线,求∠P与∠A之间的关系?
(2)如图2,BP、CP为∠ABC和∠ACE的角平分线,求∠P与∠A之间的关系?
(3)如图3,BP、CP为∠CBD和∠BCE的角平分线,求∠P与∠A之间的关系?
(请选择其中一道小题写出详细过程)
26.在苏科版七年级(下)册数学教材第12章证明中,我们学习了一个定理证明“三角形的内角和是180°”.
(1)请你根据你的课堂学习回忆并证明“三角形的内角和是180°”;如图1,在△ABC中,求证:∠A+∠B+∠C=180°
(2)如图2,点A、D、C、F在一条直线上,BC∥DE.求证:∠A+∠B=∠E+∠F;
(3)如图3,AD是∠ABC的角平分线,E是BC延长线上一点.∠EAC=∠B,EF⊥AD,垂足为F.求证:EF平分∠AED.
27.如图,在小学我们通过观察、实验的方法得到了“三角形内角和是180°”的结论.
小明受到实验方法1的启发,形成了证明该结论的想法:实验1的拼接方法直观上看,是把∠1和∠2移动到∠3的右侧,且使这三个角的顶点重合,如果把这种拼接方法抽象为几何图形,那么利用平行线的性质就可以解决问题了.
(1)填空:小明的证明过程如下:
已知:如图1,三角形ABC.
求证:∠A+∠B+∠C=180°.
证明:延长BC,过点C作CM∥BA.
∴∠A=∠1(两直线平行,内错角相等),
∠B=∠2( ).
∵∠1+∠2+∠ACB=180°( ),
∴∠A+∠B+∠ACB=180°.
(2)请你参考小明解决问题的思路与方法,画出实验2几何图形,并写出利用实验2证明该结论的过程.
(3)在实验过程中,小超不小心把三个角都撕下来,但他发现,除了可以利用原三角形三个顶点外,还可以在原三角形所在的平面内,将撕下来三个角的顶点重合在平面内任意一点,使撕下来角的两边分别平行(或重合)于原三角形的两边,也可以证明三角形内角和是180°.请你参考小超解决问题的思路与方法,画出几何图形,并写出一种证明该结论的过程.
参考答案与试题解析
一.选择题
1.【分析】根据邻补角的定义求得△ABC的两个内角∠ABC、∠ACB的度数;然后利用△ABC的内角和是180°来求∠A的度数即可.
【解答】解:∵∠DBA=120°,∠ECA=125°,
∴∠ABC=180°﹣∠DBA=60°,∠ACB=180°﹣∠ECA=55°,
∴∠A=180°﹣∠ABC﹣∠ACB=180°﹣60°﹣55°=75°,即∠A=65°.
故选:A.
【点评】本题考查了三角形内角和定理.解答该题时,先利用了邻补角的性质求得△ABC的两个内角∠ABC、∠ACB的度数,然后由三角形内角和定理求得∠A的度数.当然了,也可以利用三角形外角的性质来求∠A的度数.
2.【分析】先由三角形外角的性质得出∠3=∠B+∠1,再由∠3=80°,∠B=∠1即可得出∠1的度数,最后根据角的和差可以求出∠2的度数.
【解答】解:∵∠3是△ABD的一个外角,
∴∠3=∠B+∠1,
又∵∠3=80°,∠B=∠1,
∴∠1∠380°=40°,
∵∠BAC=70°,
∴∠2=∠BAC﹣∠1=70°﹣40°=30°.
故选:C.
【点评】本题考查了三角形外角的性质,熟知三角形的一个外角等于和它不相邻的两个外角是解答此题的关键.
3.【分析】利用平分线的性质,三角形的内角和定理以及外角的性质计算.
【解答】解:∵∠CAD=65°,AD平分∠CAE,
∴∠CAE=2∠CAD=130°,
∴∠BAC=180°﹣130°=50°,
∵∠B=30°,
∴∠ACD=∠B+∠BAC=30°+50°=80°.
故选:D.
【点评】此题主要考查角平分线的性质,三角形的内角和定理以及外角的性质.
4.【分析】根据三角形内角和定理求出∠ACB,再根据平移的性质得出∠F=∠ACB,再得出答案即可.
【解答】解:∵∠A=80°,∠B=36°,
∴∠ACB=180°﹣∠A﹣∠B=180°﹣80°﹣36°=64°,
∵将△ABC沿直线BC向右平移到△DEF的位置,
∴∠F=∠ACB=64°,
故选:C.
【点评】本题考查了三角形内角和定理和平移的性质,能根据平移的性质得出∠F=∠ACB是解此题的关键.
5.【分析】利用三角形的外角与内角间关系先求出∠ACD,再利用角平分线的性质和平行线的性质求出∠EDC.
【解答】解:∵CD是∠ACB的角平分线,
∴∠BCD=∠ACD.
∵∠BDC=∠A+∠ACD,
∴80°=60°+∠ACD.
∴∠ACD=∠BCD=20°.
∵DE∥BC,
∴∠EDC=∠BCD=20°.
故选:B.
【点评】本题主要考查了三角形的内角和定理及平行线的性质,掌握“三角形的外角等于与它不相邻的两个内角的和”、“两直线平行,内错角相等”是解决本题的关键.
6.【分析】设其三个内角分别是2k,3k,5k.根据三角形的内角和是180°,列方程即可求得三个内角的度数,然后根据角的度数判断三角形的形状.
【解答】解:设其三个内角分别是2k,3k,5k.
根据三角形的内角和定理,得2k+3k+5k=180°,
解得k=18°.
则2k=36°,3k=54°,5k=90°.
则该三角形是直角三角形.
故选:B.
【点评】此题考查了三角形的内角和定理以及三角形的分类.掌握三角形的内角和定理是解题的关键.
7.【分析】根据平角定义求出∠BDE,根据折叠性质得出∠BCD=∠ACDACB,∠BDC=∠EDC∠BDE,求出∠ACD和∠CDE,再根据三角形内角和定理求出答案即可.
【解答】解:∵∠ADE=24°,
∴∠BDE=180°﹣∠ADE=156°,
∵将△ABC沿CD折叠,点B落在边AC的点E处,
∴∠BCD=∠ACD,∠BDC=∠EDC∠BDE78°,
∵∠ACB=80°,
∴∠ACD=∠BCDACB=40°,
∴∠A=180°﹣∠ACD﹣∠ADE﹣∠CDE=180°﹣40°﹣78°﹣24°=38°,
故选:C.
【点评】本题考查了折叠性质和三角形内角和定理,能根据折叠得出∠BCD=∠ACD和∠BDC=∠EDC是解此题的关键.
8.【分析】根据BF平分∠ABC可得,∠FBC∠ABC,同理,然后根据∠BFC=125°,利用三角形内角和可得∠∠FBC+∠FCB=55°,从而得到∠ABC+∠ACB=110°,再根据三角形内角和得到∠A=70°.
【解答】解:在△FBC中,∠BFC=125°.
∴∠FBC+∠FCB=180°﹣∠BFC=55°.
∵BF平分∠ABC,CF平分∠ACB.
∴∠ABC=2∠FBC,∠ACB=2∠FCB.
∴∠ABC+∠ACB=2(∠FBC+∠FCB)=110°.
∴在△ABC中,∠A=180°﹣(∠ABC+∠ACB)=70°.
故选:C.
【点评】本题考查了三角形内角和定理与角平分线的定义,熟练掌握三角形内角和定理是解题的关键.
9.【分析】利用角平分线的定义得到∠DAP=∠PAB,∠DCP=∠PCB,再根据对顶角相等和三角形内角和定理得到∠D+∠DAP=∠P+∠DCP,∠PAB+∠P=∠B+∠PCB,然后把两式相减得到∠P与∠D、∠B之间存在的数量关系.
【解答】解:∵∠DAB和∠BCD的平分线AP和CP相交于点P,
∴∠DAP=∠PAB,∠DCP=∠PCB,
∵∠D+∠DAP=∠P+∠DCP①,
∠PAB+∠P=∠B+∠PCB②,
∴①﹣②得:∠D﹣∠P=∠P﹣∠B,
∴2∠P=∠D+∠B,
即∠P(∠D+∠B).
故选:B.
【点评】本题考查了三角形内角和定理:从复杂的图形中找出“8”字型的图形,然后利用三角形的内角和定理确定角之间的关系.
10.【分析】根据折叠的性质,再根据邻补角的定义运用合理的推理,结合三角形内角和定理即可求出答案.
【解答】解:∵△ABC沿EF翻折,
∴∠BEF=∠B'EF,∠CFE=∠C'FE,
∴180°﹣∠AEF=∠1+∠AEF,180°﹣∠AFE=∠2+∠AFE,
∵∠1=95°,
∴∠AEF(180°﹣95°)=42.5°,
∵∠A+∠AEF+∠AFE=180°,
∴∠AFE=180°﹣60°﹣42.5°=77.5°,
∴180°﹣77.5°=∠2+77.5°,
∴∠2=25°,
故选:C.
【点评】本题考查了折叠的性质,解题关键在于根据轴对称变化关系找到对应边,对应角.
11.【分析】根据角平分线的定义以及三角形的外角可得∠A1∠A,∠A2∠A1,∠A3∠A2以此类推,然后代入计算即可.
【解答】解:∵∠BA1是∠ABC的平分线,CA1是∠ACD和∠ACD的平分线,
∴∠ABA1=∠A1BC∠ABC,∠ACA1=∠A1CD∠ACD,
又∵∠ACD=∠A+∠ABC,∠A1CD=∠A1+∠A1BC,
∴∠A1∠A,
同理可得,∠A2∠A1,∠A3∠A2,
∴∠A3∠A52°=6.5°,
故选:D.
【点评】本题考查三角形的内角和,掌握三角形的内角和是180°以及三角形的一个外角等于与它不相邻的两个内角的和是解决问题的关键.
12.【分析】根据题意画出图形,①高AD在△ABC的内部时,②高AD在△ABC的外部时,根据三角形内角和定理求出∠BAD,再求出答案即可.
【解答】解:有两种情况:
①高AD在△ABC的内部时,如图1,
∵AD是高,
∴∠ADB=90°,
∵∠ABC=55°,
∴∠BAD=90°∠ABC=35°,
∵∠DAC=15°,
∴∠BAC=∠BAD+∠DAC=35°+15°=50°;
②高AD在△ABC的外部时,如图2,
∠BAC=∠BAD﹣∠DAC=35°﹣15°=20°;
所以∠BAC的度数是20°或50°,
故选:C.
【点评】本题考查了三角形内角和定理,能画出符合题意的两种图形是解此题的关键.
二.填空题
13.【分析】根据任意凸四边形内角和是360°,对顶角相等即可.
【解答】解:∵∠B=50°,∠CEB=∠ADB﹣90°,
∴∠EHD=180°﹣50°=130°,
又∵∠EHD=∠AHC,
∴∠AHC=130°,
故答案为:130.
【点评】本题考查三角形内角和定理,任意一个凸四边形可以分为两个三角形,所以任意一个凸四边形内角和是360°,再根据对顶角相等即可.
14.【分析】根据三角形内角和为180度可得∠B+∠C的度数,然后再根据四边形内角和为360°可得∠1+∠2的度数.
【解答】解:∵△ABC中,∠A=65°,
∴∠B+∠C=180°﹣65°=115°,
∵∠B+∠C+∠1+∠2=360°,
∴∠1+∠2=360°﹣115°=245°,
故答案为:245.
【点评】此题主要考查了三角形内角和,关键是掌握三角形内角和为180°.
15.【分析】根据三角形内角和定理求出∠BAC和∠DAC,求出∠EAC,即可求出答案.
【解答】解:在△ABC中,∠B=80°,∠C=42°,
∴∠BAC=180°﹣∠B﹣∠C=58°,
∵AE平分∠BAC,
∴∠EAC∠BAC,
∵AD⊥BC,
∴∠ADC=90°,
∴∠DAC=180°﹣∠ADC﹣∠C=180°﹣90°﹣42°=48°,
∴∠DAE=∠DAC﹣∠EAC=48°﹣29°=19°,
故答案为:19°.
【点评】本题考查了三角形内角和定理,垂直定义,角平分线的定义等知识点,能求出∠DAC和∠EAC的度数是解此题的关键.
16.【分析】先根据∠AFC是△ABF与△CDF的外角得出,∠B+∠BAD=∠D+∠DCB,再根据AE、CE分别平分∠BAD、∠DCB得出∠BAE=∠EAD∠BAD,∠DCE=∠BCE∠BCD,根据三角形外角的性质即可得出结论.
【解答】解:设BC与AE、BC与AD、AD与CE,分别相交于H、F、G,如图:
∵∠AFC是△ABF与△CDF的外角,
∴∠B+∠BAD=∠D+∠DCB.
∵AE、CE分别平分∠BAD、∠DCB,
∴∠BAE=∠EAD∠BAD,∠DCE=∠BCE∠BCD.
∵∠AHC是△ABH与△CEH的外角,
∴∠E∠DAB=∠D∠DCB①,
同理可得,∠E∠DCB=∠B∠BAD②,
①+②得,2∠E=∠B+∠D,
∵∠B=32°,∠E=35°,
∴∠D=2×35°﹣32°=38°.
故答案为:38°.
【点评】本题考查的是三角形外角的性质,熟知三角形的一个外角等于和它不相邻的两个内角的和是解答此题的关键.
17.【分析】根据图示,可得:∠D+∠E=∠ABC+∠BAC,∠F+∠G=∠ABC+∠ACB,∠H+∠I=∠ACB+∠BAC,再根据三角形的内角和定理,求出∠D+∠E+∠F+∠G+∠H+∠I的值即可.
【解答】解:在△ABC和△CDE中,
∵∠ACB=∠DCE,
∴∠D+∠E=∠ABC+∠BAC;
在△ABC和△AFG中,
∵∠BAC=∠FAG,
∴∠F+∠G=∠ABC+∠ACB;
在△ABC和△HBI中,
∵∠ABC=∠HBI,
∴∠H+∠I=∠ACB+∠BAC,
∴∠D+∠E+∠F+∠G+∠H+∠I
=(∠ABC+∠BAC)+(∠ABC+∠ACB)+(∠ACB+∠BAC)
=2(∠ABC+∠BAC+∠ACB)
=2×180
=360°.
故答案为:360.
【点评】此题主要考查了三角形的内角和定理,解答此题的关键是要明确:三角形内角和是180°.
18.【分析】先利用对折的性质说明∠ADE与∠A′DE、∠AED与∠A′ED的关系,再利用三角形的内角和、平角的定义求出∠ADE、∠DEA′、∠DEC的度数,最后利用角的和差关系求出∠CEA′的度数.
【解答】解:∵△A′DE是△ADE沿DE对折后的图形,
∴∠ADE=∠A′DE,∠AED=∠A′ED.
∵∠ADE+∠A′DE+∠BDA′=180°,∠BDA′=86°,
∴∠ADE=47°.
∵∠A+∠ADE+∠AED=180°,∠A=30°,
∴∠AED=∠DEA′=100°.
∵∠AED+∠DEC=180°,
∴∠DEC=77°.
∵∠DEA′=103°,
∴∠CEA′=∠DEA′﹣∠DEC=26°.
故答案为:26°.
【点评】本题主要考查了三角形的内角和、平角的定义,掌握角的和差关系、“三角形的内角和是180°”及平角的定义是解决本题的关键.
19.【分析】由角平分线的定义及三角形的内角和定理可得∠CBF+∠BCF=120°,进而利用平角定义和三角形的内角和定理求解.
【解答】解:∵BF平分∠DBC,CF平分∠ECB,
∴∠ECB=2∠BCF,∠DBC=2∠CBF,
∵∠F=60°,
∴∠CBF+∠BCF=180°﹣60°=120°,
∴∠ECB+∠DBC=2×120°=240°,
∴∠ABC+∠ACB=360°﹣(∠ECB+∠DBC)=360°﹣240°=120°,
∴∠A=180°﹣120°=60°.
故答案为:60°.
【点评】本题考查三角形外角的性质及三角形的内角和定理,解答的关键是熟练应用外角和内角的关系.
20.【分析】根据角平分线的定义可得∠A1BD∠ABC,∠A1CD∠ACD,再根据三角形外角的性质可得(∠ABC+∠A)∠ABC+∠A1,化简可得∠A1∠A,进一步找出其中的规律,即可求出∠A2022的度数.
【解答】解:∵BA1和CA1分别是△ABC的内角平分线和外角平分线,
∴∠A1BD∠ABC,∠A1CD∠ACD,
又∵∠ACD=∠ABC+∠A,∠A1CD=∠A1BD+∠A1,
∴(∠ABC+∠A)∠ABC+∠A1,
∴∠A1∠A,
同理可得:∠A2∠A1∠A,
∠A3∠A,......
则A2022∠A,
∵∠A=α,
∴∠A2022,
故答案为:.
【点评】本题考查了三角形的内角和定理,三角形外角的性质,角平分线的定义等,找出∠A1,∠A2,∠A3与∠A的规律是解题的关键.
三.解答题
21.【分析】(1)由角平分线的定义可得∠DAC=30°,再由三角形外角性质即可求∠ADB的度数;
(2)由三角形的外角性质可得∠BAD+∠ABE=45°,再由角平分线的定义得∠BAC=2∠BAD,∠ABC=2∠ABE,从而得∠BAC+∠ABC=90°,利用三角形的内角和即可求∠C的度数.
【解答】解:(1)∵AD平分∠BAC,∠BAC=80°,
∴∠DAC∠BAC=40°,
∵∠ADB是△ADC的外角,∠C=60°,
∴∠ADB=∠C+∠DAC=100°;
(2)∵∠BED是△ABE的外角,∠BED=60°,
∴∠BAD+∠ABE=∠BED=60°,
∵AD平分∠BAC,BE平分∠ABC,
∴∠BAC=2∠BAD,∠ABC=2∠ABE,
∴∠BAC+∠ABC=2(∠BAD+∠ABE)=120°,
∵∠BAC+∠ABC+∠C=180°,
∴∠C=180°﹣(∠BAC+∠ABC)=60°.
【点评】本题主要考查三角形的内角和定理,解答的关键是结合图形分析清楚各角之间的关系.
22.【分析】(1)根据平行线的性质,由DE∥BC,得∠2=∠EBC,进而推断出∠EBC=∠1.根据平行线的判定,得FG∥BE.
(2)根据角平分线的定义,得∠ABC=2∠EBC=60°.再根据三角形内角和定理求得∠A=180°﹣∠ABC﹣∠C=70°.
【解答】解:(1)∵DE∥BC,
∴∠2=∠EBC.
又∵∠1=∠2,
∴∠EBC=∠1.
∴FG∥BE.
(2)由(1)得,∠EBC=∠2=30°.
∵BE为∠ABC的角平分线,
∴∠ABC=2∠EBC=60°.
∴∠A=180°﹣∠ABC﹣∠C=70°.
【点评】本题主要考查平行线的性质与判定、角平分线的定义、三角形内角和定理,熟练掌握平行线的性质与判定、角平分线的定义、三角形内角和定理是解决本题的关键.
23.【分析】(1)根据三角形内角和定理求出∠BAC=180°﹣∠B﹣∠C=76°,根据角平分线定义得出∠BAE=∠CAEBAC,即可求出答案;
(2)根据垂直定义得出∠ADC=90°,∠AFD=90°,根据直角三角形的两锐角互余得出∠DAC=90°﹣∠C=20°,求出∠DAE,再根据直角三角形的两锐角互余求出答案即可.
【解答】解:(1)∵∠B=34°,∠C=70°,
∴∠BAC=180°﹣∠B﹣∠C=76°,
∵AE平分∠BAC,
∴∠BAE=∠CAEBAC76°=38°;
(2)∵AD⊥BC,
∴∠ADC=90°,
∵∠C=70°,
∴∠DAC=90°﹣∠C=20°,
∵∠EAC=38°,
∴∠DAE=∠EAC﹣∠DAC=38°﹣20°=18°,
∵DF⊥AE,
∴∠AFD=90°,
∴∠ADF=90°﹣∠DAE=90°﹣18°=72°.
【点评】本题考查了三角形内角和定理,角平分线的定义和直角三角形的性质等知识点,能熟记三角形内角和定理等于180°和直角三角形的两锐角互余是解此题的关键.
24.【分析】(1)由题意可得∠AEC=90°,则由三角形的内角和定理可求得∠BAC=80°,∠CAE=20°,再由角平分线的定义得∠CAD=40°,即可求∠DAE的度数;
(2)由三角形的内角和定理可求得∠BAC=84°,再由角平分线的定义得∠CAD=42°,再由三角形的内角和定理求得∠ADC=70°,由对顶角相等得∠EDF=70°,结合FE⊥BC,即可求解;
(3)由角平分线的定义得∠BAD=∠CAD,∠AEC=∠AED,再由三角形的内角和定理得∠AEC=180°﹣∠C﹣∠CAE,由三角形的外角性质得∠ADE=∠B+∠BAD,再结合∠ADE+∠AED+∠DAE=180°,即可求解.
【解答】解:(1)∵AE⊥BC,
∴∠AEC=90°,
∵∠B=30°,C=70°,
∴∠BAC=180°﹣∠B﹣∠C=80°,
∠CAE=180°﹣∠AEC﹣∠C=20°,
∵AD平分∠BAC,
∴∠CAD∠BAC=40°,
∴∠DAE=∠CAD﹣∠CAE=20°;
(2)∵∠B=28°,∠C=68°,
∴∠BAC=180°﹣∠B﹣∠C=84°,
∵AD平分∠BAC,
∴∠CAD∠BAC=42°,
∴∠ADC=180°﹣∠C﹣∠CAD=70°,
∴∠EDF=∠ADC=70°,
∵FE⊥BC,
∴∠DEF=90°,
∴∠DFE=180°﹣∠DEF﹣∠EDF=20°;
(3)∵AD平分∠BAC,EA平分∠BEC,
∴∠BAD=∠CAD,∠AEC=∠AED,
∵∠AEC=180°﹣∠C﹣∠CAE,∠ADE=∠B+∠BAD,
∠ADE+∠AED+∠DAE=180°,∠CAE=∠CAD﹣∠DAE,
∴∠B+∠BAD+180°﹣∠C﹣∠CAD+∠DAE+∠DAE=180°,
整理得:2∠DAE=∠C﹣∠B,
∵∠C﹣∠B=38°,
∴2∠DAE=38°,
∴∠DAE=19°.
【点评】本题主要考查三角形的内角和定理,解答的关键是结合图形分析清楚各角之间的关系.
25.【分析】(1)根据角平分线的定义,由BP、CP为∠ABC和∠ACB的角平分线,得∠CBP,∠BCP,推断出∠CBP+∠CBP.根据三角形的内角和定理,∠ABC+∠ACB=180°﹣∠A,那么∠PBC+∠PCB,进而推断出∠P=180°﹣(∠PBC+∠PCB)=90°.
(2)根据三角形外角的性质,得∠P=∠PCD﹣∠PBC.根据角平分线的定义,得∠PCD,∠PBC,那么∠P.
(3)根据三角形外角的性质,得∠DBC=∠A+∠ACB,∠BCE=∠A+∠ABC,那么∠DBC+∠BCE=180°+∠A.根据角平分线的定义,BP、CP为∠CBD和∠BCE的角平分线,
得∠CBP,∠BCP,那么,那么∠P=180°﹣(∠CBP+∠BCP)=90°.
【解答】解:(1)∵BP、CP为∠ABC和∠ACB的角平分线,
∴∠CBP,∠BCP.
∴∠CBP+∠CBP.
∵∠A+∠ABC+∠ACB=180°,
∴∠ABC+∠ACB=180°﹣∠A.
∴∠PBC+∠PCB.
∴∠P=180°﹣(∠PBC+∠PCB)=180°90°.
(2)∵∠P+∠PBC=∠PCD,
∴∠P=∠PCD﹣∠PBC.
∵BP、CP为∠ABC和∠ACE的角平分线,
∴∠PCD,∠PBC.
∴∠P.
(3)∵∠DBC=∠A+∠ACB,∠BCE=∠A+∠ABC,
∴∠DBC+∠BCE=∠A+∠ACB+∠A+∠ABC=180°+∠A.
∵BP、CP为∠CBD和∠BCE的角平分线,
∴∠CBP,∠BCP.
∴.
∴∠P=180°﹣(∠CBP+∠BCP)=180°90°.
【点评】本题主要考查角平分线的定义、三角形外角的性质,熟练掌握角平分线的定义以及三角形外角的性质是解决本题的关键.
26.【分析】(1)通过作平行线,利用平行线的性质,将三角形的三个内角“集中”到一个顶点处的邻补角即可;
(2)利用平行线的性质和三角形的内角和定理可得结论;
(3)利用角平分线的定义,三角形的内角和定理以及等腰三角形的判定和性质可得结论.
【解答】解:(1)如图1,延长BC,过点C作CE∥AB,
∵CE∥AB,
∴∠A=∠ACE,∠B=∠DCE,
又∵∠ACB+∠ACE+∠DCE=180°,
∴∠A+∠B+∠ACB=180°;
(2)如图2,
∵BC∥DE.
∴∠ACB=∠EDF,
又∵∠A+∠B+∠ACB=180°=∠E+∠F+∠EDF,
∴∠A+∠B=∠E+∠F;
(3)如图3,
∵AD是∠ABC的角平分线,
∴∠BAD=∠CAD∠BAC,
∵∠EAF=∠EAC+∠CAD,∠ADE=∠BAD+∠B,∠EAC=∠B,
∴∠EAD=∠ADE,
∴EA=ED,
又∵EF⊥AD,
∴∠AEF=∠DEF,
即EF平分∠AED.
【点评】本题考查平行线的性质,角平分线的定义,等腰三角形的判定和性质以及三角形内角和定理,掌握平行线的性质,角平分线的定义,等腰三角形的判定和性质以及三角形内角和定理是正确解答的前提.
27.【分析】(1)由证明过程,结合具体的图形可得答案;
(2)过点A作DE∥BC,利用平行线的性质以及平角的定义可得结论;
(3)在BC边上任取一点D,分别作DE∥AB,DF∥AC,利用平行线的性质和平角的定义可得答案.
【解答】解:(1)故答案为:两直线平行,同位角相等,平角定义;
(2)证明:如图2,过点A作DE∥BC,
∵DE∥BC,
∴∠B=∠BAD,∠C=∠CAE.
∵∠BAD+∠BAC+∠CAE=180°,
∴∠BAC+∠B+∠C=180°;
(3)如图3,过点D作DE∥AB,DF∥AC,
∵DE∥AB,
∴∠B=∠CDE,∠BFD=∠EDF.
∵DF∥AC,
∴∠C=∠BDF,∠BFD=∠A.
∴∠A=∠EDF.
∵∠BDF+∠EDF+∠CDE=180°,
∴∠BAC+∠B+∠C=180°.
【点评】本题考查三角形的内角和定理,掌握平行线的性质以及平角的定义是解决问题的前提.
一.选择题
1.如图所示,考古学家发现在地下A处有一座古墓,古墓上方是煤气管道,为了不影响管道,准备在B和C处开工挖出“V”字形通道,如果∠DBA=120°,∠ECA=125°,则∠A的度数是( )
A.65° B.80° C.85° D.90°
2.如图,D是△ABC的BC边上一点,∠B=∠1,∠3=80°,∠BAC=70°.则∠2的大小是( )
A.20° B.25° C.30° D.35°
3.如图,∠B=30°,∠CAD=65°且AD平分∠CAE,则∠ACD等于( )
A.95° B.65° C.50° D.80°
4.如图,在△ABC中,∠A=80°,∠B=36°,将△ABC沿直线BC向右平移到△DEF的位置,则∠F的度数是( )
A.80° B.36° C.64° D.116°
5.如图,在△ABC中,CD是∠ACB的角平分线交AB于点D,DE∥BC,交AC于点E,∠A=60°,∠BDC=80°,则∠EDC的度数为( )
A.10° B.20° C.30° D.40°
6.在一个三角形中,三个内角之比为2:3:5,则这个三角形是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.无法确定
7.如图,在△ABC中,∠ACB=80°,点D在AB上,将△ABC沿CD折叠,点B落在边AC的点E处.若∠ADE=24°,则∠A的度数为( )
A.24° B.32° C.38° D.48°
8.如图,在△ABC中,BF平分∠ABC,CF平分∠ACB,∠BFC=125°,则∠A的度数为( )
A.60° B.80° C.70° D.45°
9.如图,线段AB、CD相交于点O,连接AD、CB,∠DAB和∠BCD的平分线AP和CP相交于点P,则∠P与∠D、∠B之间存在的数量关系为( )
A.∠P=2(∠B﹣∠D) B.
C. D.
10.如图,把△ABC沿EF翻折,叠合后的图形如图,若∠A=60°,∠1=95°,则∠2的度数是( )
A.15° B.20° C.25° D.35°
11.如图,在△ABC中,∠A=52°,∠ABC和∠ACD的平分线交于点A1,得∠A1,∠A1BC和∠A1CD的平分线交于点A2,得∠A2,同理可得∠A3,则∠A3=( )度.
A.26° B.15° C.10° D.6.5°
12.在△ABC中,∠B=55°,AD是△ABC的边BC上的高.∠DAC=15°,则∠BAC等于( )
A.20° B.50° C.20°或50° D.35°
二.填空题
13.如图,在△ABC中,AD⊥BC,CE⊥AB,且AD与CE交于点H,若∠B=50°,则∠AHC的度数为 °.
14.如图,在△ABC中,∠A=65°,则∠1+∠2= °.
15.如图,在△ABC中,∠B=80°,∠C=42°,AD⊥BC于点D,AE平分∠BAC,则∠DAE= .
16.如图,AE,CE分别平分∠BAD和∠BCD,∠B=32°,∠E=35°,则∠D= .
17.如图,直线GD、EH、FI两两相交于点A、B、C,则∠D+∠E+∠F+∠G+∠H+∠I= °.
18.如图,在△ABC中,沿DE折叠,点A落在三角形所在的平面内的点为A′,若∠A=30°,∠BDA′=86°,则∠CEA′的度数为 .
19.如图,∠DBC与∠ECB是△ABC的两个外角,BF平分∠DBC交∠ECB的平分线于点F.若∠F=60°,则∠A= .
20.如图,BA1和CA1分别是△ABC的内角平分线和外角平分线,BA2是∠A1BD的角平分线,CA2是∠A1CD的角平分线,BA3是∠A2BD的角平分线,CA3是∠A2CD的角平分线,若∠A=α,则∠A2022= .
三.解答题
21.如图所示,在△ABC中,AD平分∠BAC交BC于点D,BE平分∠ABC交AD于点E.
(1)若∠C=60°,∠BAC=80°,求∠ADB的度数;
(2)若∠BED=60°,求∠C的度数.
22.如图,在△ABC中,若∠1=∠2,DE∥BC.
(1)试说明FG∥BE;
(2)若BE为∠ABC的角平分线,∠2=30°,∠C=50°,求∠A的度数.
23.如图,在△ABC中,∠B=34°,∠C=70°,AD⊥BC于点D,AE平分∠BAC交BC于点E,DF⊥AE于点F.
(1)求∠BAE的度数;
(2)求∠ADF的度数.
24.(1)如图1,AD平分∠BAC,AE⊥BC,∠B=30°,C=70°,求∠DAE的度数;
(2)如图2,AD平分∠BAC,点F在AD的延长线上,FE⊥BC,∠B=28°,∠C=68°,求∠DFE的度数;
(3)如图3,AD平分∠BAC,EA平分∠BEC,∠C﹣∠B=38°,求∠DAE的度数.
25.在△ABC中,
(1)如图1,BP、CP为∠ABC和∠ACB的角平分线,求∠P与∠A之间的关系?
(2)如图2,BP、CP为∠ABC和∠ACE的角平分线,求∠P与∠A之间的关系?
(3)如图3,BP、CP为∠CBD和∠BCE的角平分线,求∠P与∠A之间的关系?
(请选择其中一道小题写出详细过程)
26.在苏科版七年级(下)册数学教材第12章证明中,我们学习了一个定理证明“三角形的内角和是180°”.
(1)请你根据你的课堂学习回忆并证明“三角形的内角和是180°”;如图1,在△ABC中,求证:∠A+∠B+∠C=180°
(2)如图2,点A、D、C、F在一条直线上,BC∥DE.求证:∠A+∠B=∠E+∠F;
(3)如图3,AD是∠ABC的角平分线,E是BC延长线上一点.∠EAC=∠B,EF⊥AD,垂足为F.求证:EF平分∠AED.
27.如图,在小学我们通过观察、实验的方法得到了“三角形内角和是180°”的结论.
小明受到实验方法1的启发,形成了证明该结论的想法:实验1的拼接方法直观上看,是把∠1和∠2移动到∠3的右侧,且使这三个角的顶点重合,如果把这种拼接方法抽象为几何图形,那么利用平行线的性质就可以解决问题了.
(1)填空:小明的证明过程如下:
已知:如图1,三角形ABC.
求证:∠A+∠B+∠C=180°.
证明:延长BC,过点C作CM∥BA.
∴∠A=∠1(两直线平行,内错角相等),
∠B=∠2( ).
∵∠1+∠2+∠ACB=180°( ),
∴∠A+∠B+∠ACB=180°.
(2)请你参考小明解决问题的思路与方法,画出实验2几何图形,并写出利用实验2证明该结论的过程.
(3)在实验过程中,小超不小心把三个角都撕下来,但他发现,除了可以利用原三角形三个顶点外,还可以在原三角形所在的平面内,将撕下来三个角的顶点重合在平面内任意一点,使撕下来角的两边分别平行(或重合)于原三角形的两边,也可以证明三角形内角和是180°.请你参考小超解决问题的思路与方法,画出几何图形,并写出一种证明该结论的过程.
参考答案与试题解析
一.选择题
1.【分析】根据邻补角的定义求得△ABC的两个内角∠ABC、∠ACB的度数;然后利用△ABC的内角和是180°来求∠A的度数即可.
【解答】解:∵∠DBA=120°,∠ECA=125°,
∴∠ABC=180°﹣∠DBA=60°,∠ACB=180°﹣∠ECA=55°,
∴∠A=180°﹣∠ABC﹣∠ACB=180°﹣60°﹣55°=75°,即∠A=65°.
故选:A.
【点评】本题考查了三角形内角和定理.解答该题时,先利用了邻补角的性质求得△ABC的两个内角∠ABC、∠ACB的度数,然后由三角形内角和定理求得∠A的度数.当然了,也可以利用三角形外角的性质来求∠A的度数.
2.【分析】先由三角形外角的性质得出∠3=∠B+∠1,再由∠3=80°,∠B=∠1即可得出∠1的度数,最后根据角的和差可以求出∠2的度数.
【解答】解:∵∠3是△ABD的一个外角,
∴∠3=∠B+∠1,
又∵∠3=80°,∠B=∠1,
∴∠1∠380°=40°,
∵∠BAC=70°,
∴∠2=∠BAC﹣∠1=70°﹣40°=30°.
故选:C.
【点评】本题考查了三角形外角的性质,熟知三角形的一个外角等于和它不相邻的两个外角是解答此题的关键.
3.【分析】利用平分线的性质,三角形的内角和定理以及外角的性质计算.
【解答】解:∵∠CAD=65°,AD平分∠CAE,
∴∠CAE=2∠CAD=130°,
∴∠BAC=180°﹣130°=50°,
∵∠B=30°,
∴∠ACD=∠B+∠BAC=30°+50°=80°.
故选:D.
【点评】此题主要考查角平分线的性质,三角形的内角和定理以及外角的性质.
4.【分析】根据三角形内角和定理求出∠ACB,再根据平移的性质得出∠F=∠ACB,再得出答案即可.
【解答】解:∵∠A=80°,∠B=36°,
∴∠ACB=180°﹣∠A﹣∠B=180°﹣80°﹣36°=64°,
∵将△ABC沿直线BC向右平移到△DEF的位置,
∴∠F=∠ACB=64°,
故选:C.
【点评】本题考查了三角形内角和定理和平移的性质,能根据平移的性质得出∠F=∠ACB是解此题的关键.
5.【分析】利用三角形的外角与内角间关系先求出∠ACD,再利用角平分线的性质和平行线的性质求出∠EDC.
【解答】解:∵CD是∠ACB的角平分线,
∴∠BCD=∠ACD.
∵∠BDC=∠A+∠ACD,
∴80°=60°+∠ACD.
∴∠ACD=∠BCD=20°.
∵DE∥BC,
∴∠EDC=∠BCD=20°.
故选:B.
【点评】本题主要考查了三角形的内角和定理及平行线的性质,掌握“三角形的外角等于与它不相邻的两个内角的和”、“两直线平行,内错角相等”是解决本题的关键.
6.【分析】设其三个内角分别是2k,3k,5k.根据三角形的内角和是180°,列方程即可求得三个内角的度数,然后根据角的度数判断三角形的形状.
【解答】解:设其三个内角分别是2k,3k,5k.
根据三角形的内角和定理,得2k+3k+5k=180°,
解得k=18°.
则2k=36°,3k=54°,5k=90°.
则该三角形是直角三角形.
故选:B.
【点评】此题考查了三角形的内角和定理以及三角形的分类.掌握三角形的内角和定理是解题的关键.
7.【分析】根据平角定义求出∠BDE,根据折叠性质得出∠BCD=∠ACDACB,∠BDC=∠EDC∠BDE,求出∠ACD和∠CDE,再根据三角形内角和定理求出答案即可.
【解答】解:∵∠ADE=24°,
∴∠BDE=180°﹣∠ADE=156°,
∵将△ABC沿CD折叠,点B落在边AC的点E处,
∴∠BCD=∠ACD,∠BDC=∠EDC∠BDE78°,
∵∠ACB=80°,
∴∠ACD=∠BCDACB=40°,
∴∠A=180°﹣∠ACD﹣∠ADE﹣∠CDE=180°﹣40°﹣78°﹣24°=38°,
故选:C.
【点评】本题考查了折叠性质和三角形内角和定理,能根据折叠得出∠BCD=∠ACD和∠BDC=∠EDC是解此题的关键.
8.【分析】根据BF平分∠ABC可得,∠FBC∠ABC,同理,然后根据∠BFC=125°,利用三角形内角和可得∠∠FBC+∠FCB=55°,从而得到∠ABC+∠ACB=110°,再根据三角形内角和得到∠A=70°.
【解答】解:在△FBC中,∠BFC=125°.
∴∠FBC+∠FCB=180°﹣∠BFC=55°.
∵BF平分∠ABC,CF平分∠ACB.
∴∠ABC=2∠FBC,∠ACB=2∠FCB.
∴∠ABC+∠ACB=2(∠FBC+∠FCB)=110°.
∴在△ABC中,∠A=180°﹣(∠ABC+∠ACB)=70°.
故选:C.
【点评】本题考查了三角形内角和定理与角平分线的定义,熟练掌握三角形内角和定理是解题的关键.
9.【分析】利用角平分线的定义得到∠DAP=∠PAB,∠DCP=∠PCB,再根据对顶角相等和三角形内角和定理得到∠D+∠DAP=∠P+∠DCP,∠PAB+∠P=∠B+∠PCB,然后把两式相减得到∠P与∠D、∠B之间存在的数量关系.
【解答】解:∵∠DAB和∠BCD的平分线AP和CP相交于点P,
∴∠DAP=∠PAB,∠DCP=∠PCB,
∵∠D+∠DAP=∠P+∠DCP①,
∠PAB+∠P=∠B+∠PCB②,
∴①﹣②得:∠D﹣∠P=∠P﹣∠B,
∴2∠P=∠D+∠B,
即∠P(∠D+∠B).
故选:B.
【点评】本题考查了三角形内角和定理:从复杂的图形中找出“8”字型的图形,然后利用三角形的内角和定理确定角之间的关系.
10.【分析】根据折叠的性质,再根据邻补角的定义运用合理的推理,结合三角形内角和定理即可求出答案.
【解答】解:∵△ABC沿EF翻折,
∴∠BEF=∠B'EF,∠CFE=∠C'FE,
∴180°﹣∠AEF=∠1+∠AEF,180°﹣∠AFE=∠2+∠AFE,
∵∠1=95°,
∴∠AEF(180°﹣95°)=42.5°,
∵∠A+∠AEF+∠AFE=180°,
∴∠AFE=180°﹣60°﹣42.5°=77.5°,
∴180°﹣77.5°=∠2+77.5°,
∴∠2=25°,
故选:C.
【点评】本题考查了折叠的性质,解题关键在于根据轴对称变化关系找到对应边,对应角.
11.【分析】根据角平分线的定义以及三角形的外角可得∠A1∠A,∠A2∠A1,∠A3∠A2以此类推,然后代入计算即可.
【解答】解:∵∠BA1是∠ABC的平分线,CA1是∠ACD和∠ACD的平分线,
∴∠ABA1=∠A1BC∠ABC,∠ACA1=∠A1CD∠ACD,
又∵∠ACD=∠A+∠ABC,∠A1CD=∠A1+∠A1BC,
∴∠A1∠A,
同理可得,∠A2∠A1,∠A3∠A2,
∴∠A3∠A52°=6.5°,
故选:D.
【点评】本题考查三角形的内角和,掌握三角形的内角和是180°以及三角形的一个外角等于与它不相邻的两个内角的和是解决问题的关键.
12.【分析】根据题意画出图形,①高AD在△ABC的内部时,②高AD在△ABC的外部时,根据三角形内角和定理求出∠BAD,再求出答案即可.
【解答】解:有两种情况:
①高AD在△ABC的内部时,如图1,
∵AD是高,
∴∠ADB=90°,
∵∠ABC=55°,
∴∠BAD=90°∠ABC=35°,
∵∠DAC=15°,
∴∠BAC=∠BAD+∠DAC=35°+15°=50°;
②高AD在△ABC的外部时,如图2,
∠BAC=∠BAD﹣∠DAC=35°﹣15°=20°;
所以∠BAC的度数是20°或50°,
故选:C.
【点评】本题考查了三角形内角和定理,能画出符合题意的两种图形是解此题的关键.
二.填空题
13.【分析】根据任意凸四边形内角和是360°,对顶角相等即可.
【解答】解:∵∠B=50°,∠CEB=∠ADB﹣90°,
∴∠EHD=180°﹣50°=130°,
又∵∠EHD=∠AHC,
∴∠AHC=130°,
故答案为:130.
【点评】本题考查三角形内角和定理,任意一个凸四边形可以分为两个三角形,所以任意一个凸四边形内角和是360°,再根据对顶角相等即可.
14.【分析】根据三角形内角和为180度可得∠B+∠C的度数,然后再根据四边形内角和为360°可得∠1+∠2的度数.
【解答】解:∵△ABC中,∠A=65°,
∴∠B+∠C=180°﹣65°=115°,
∵∠B+∠C+∠1+∠2=360°,
∴∠1+∠2=360°﹣115°=245°,
故答案为:245.
【点评】此题主要考查了三角形内角和,关键是掌握三角形内角和为180°.
15.【分析】根据三角形内角和定理求出∠BAC和∠DAC,求出∠EAC,即可求出答案.
【解答】解:在△ABC中,∠B=80°,∠C=42°,
∴∠BAC=180°﹣∠B﹣∠C=58°,
∵AE平分∠BAC,
∴∠EAC∠BAC,
∵AD⊥BC,
∴∠ADC=90°,
∴∠DAC=180°﹣∠ADC﹣∠C=180°﹣90°﹣42°=48°,
∴∠DAE=∠DAC﹣∠EAC=48°﹣29°=19°,
故答案为:19°.
【点评】本题考查了三角形内角和定理,垂直定义,角平分线的定义等知识点,能求出∠DAC和∠EAC的度数是解此题的关键.
16.【分析】先根据∠AFC是△ABF与△CDF的外角得出,∠B+∠BAD=∠D+∠DCB,再根据AE、CE分别平分∠BAD、∠DCB得出∠BAE=∠EAD∠BAD,∠DCE=∠BCE∠BCD,根据三角形外角的性质即可得出结论.
【解答】解:设BC与AE、BC与AD、AD与CE,分别相交于H、F、G,如图:
∵∠AFC是△ABF与△CDF的外角,
∴∠B+∠BAD=∠D+∠DCB.
∵AE、CE分别平分∠BAD、∠DCB,
∴∠BAE=∠EAD∠BAD,∠DCE=∠BCE∠BCD.
∵∠AHC是△ABH与△CEH的外角,
∴∠E∠DAB=∠D∠DCB①,
同理可得,∠E∠DCB=∠B∠BAD②,
①+②得,2∠E=∠B+∠D,
∵∠B=32°,∠E=35°,
∴∠D=2×35°﹣32°=38°.
故答案为:38°.
【点评】本题考查的是三角形外角的性质,熟知三角形的一个外角等于和它不相邻的两个内角的和是解答此题的关键.
17.【分析】根据图示,可得:∠D+∠E=∠ABC+∠BAC,∠F+∠G=∠ABC+∠ACB,∠H+∠I=∠ACB+∠BAC,再根据三角形的内角和定理,求出∠D+∠E+∠F+∠G+∠H+∠I的值即可.
【解答】解:在△ABC和△CDE中,
∵∠ACB=∠DCE,
∴∠D+∠E=∠ABC+∠BAC;
在△ABC和△AFG中,
∵∠BAC=∠FAG,
∴∠F+∠G=∠ABC+∠ACB;
在△ABC和△HBI中,
∵∠ABC=∠HBI,
∴∠H+∠I=∠ACB+∠BAC,
∴∠D+∠E+∠F+∠G+∠H+∠I
=(∠ABC+∠BAC)+(∠ABC+∠ACB)+(∠ACB+∠BAC)
=2(∠ABC+∠BAC+∠ACB)
=2×180
=360°.
故答案为:360.
【点评】此题主要考查了三角形的内角和定理,解答此题的关键是要明确:三角形内角和是180°.
18.【分析】先利用对折的性质说明∠ADE与∠A′DE、∠AED与∠A′ED的关系,再利用三角形的内角和、平角的定义求出∠ADE、∠DEA′、∠DEC的度数,最后利用角的和差关系求出∠CEA′的度数.
【解答】解:∵△A′DE是△ADE沿DE对折后的图形,
∴∠ADE=∠A′DE,∠AED=∠A′ED.
∵∠ADE+∠A′DE+∠BDA′=180°,∠BDA′=86°,
∴∠ADE=47°.
∵∠A+∠ADE+∠AED=180°,∠A=30°,
∴∠AED=∠DEA′=100°.
∵∠AED+∠DEC=180°,
∴∠DEC=77°.
∵∠DEA′=103°,
∴∠CEA′=∠DEA′﹣∠DEC=26°.
故答案为:26°.
【点评】本题主要考查了三角形的内角和、平角的定义,掌握角的和差关系、“三角形的内角和是180°”及平角的定义是解决本题的关键.
19.【分析】由角平分线的定义及三角形的内角和定理可得∠CBF+∠BCF=120°,进而利用平角定义和三角形的内角和定理求解.
【解答】解:∵BF平分∠DBC,CF平分∠ECB,
∴∠ECB=2∠BCF,∠DBC=2∠CBF,
∵∠F=60°,
∴∠CBF+∠BCF=180°﹣60°=120°,
∴∠ECB+∠DBC=2×120°=240°,
∴∠ABC+∠ACB=360°﹣(∠ECB+∠DBC)=360°﹣240°=120°,
∴∠A=180°﹣120°=60°.
故答案为:60°.
【点评】本题考查三角形外角的性质及三角形的内角和定理,解答的关键是熟练应用外角和内角的关系.
20.【分析】根据角平分线的定义可得∠A1BD∠ABC,∠A1CD∠ACD,再根据三角形外角的性质可得(∠ABC+∠A)∠ABC+∠A1,化简可得∠A1∠A,进一步找出其中的规律,即可求出∠A2022的度数.
【解答】解:∵BA1和CA1分别是△ABC的内角平分线和外角平分线,
∴∠A1BD∠ABC,∠A1CD∠ACD,
又∵∠ACD=∠ABC+∠A,∠A1CD=∠A1BD+∠A1,
∴(∠ABC+∠A)∠ABC+∠A1,
∴∠A1∠A,
同理可得:∠A2∠A1∠A,
∠A3∠A,......
则A2022∠A,
∵∠A=α,
∴∠A2022,
故答案为:.
【点评】本题考查了三角形的内角和定理,三角形外角的性质,角平分线的定义等,找出∠A1,∠A2,∠A3与∠A的规律是解题的关键.
三.解答题
21.【分析】(1)由角平分线的定义可得∠DAC=30°,再由三角形外角性质即可求∠ADB的度数;
(2)由三角形的外角性质可得∠BAD+∠ABE=45°,再由角平分线的定义得∠BAC=2∠BAD,∠ABC=2∠ABE,从而得∠BAC+∠ABC=90°,利用三角形的内角和即可求∠C的度数.
【解答】解:(1)∵AD平分∠BAC,∠BAC=80°,
∴∠DAC∠BAC=40°,
∵∠ADB是△ADC的外角,∠C=60°,
∴∠ADB=∠C+∠DAC=100°;
(2)∵∠BED是△ABE的外角,∠BED=60°,
∴∠BAD+∠ABE=∠BED=60°,
∵AD平分∠BAC,BE平分∠ABC,
∴∠BAC=2∠BAD,∠ABC=2∠ABE,
∴∠BAC+∠ABC=2(∠BAD+∠ABE)=120°,
∵∠BAC+∠ABC+∠C=180°,
∴∠C=180°﹣(∠BAC+∠ABC)=60°.
【点评】本题主要考查三角形的内角和定理,解答的关键是结合图形分析清楚各角之间的关系.
22.【分析】(1)根据平行线的性质,由DE∥BC,得∠2=∠EBC,进而推断出∠EBC=∠1.根据平行线的判定,得FG∥BE.
(2)根据角平分线的定义,得∠ABC=2∠EBC=60°.再根据三角形内角和定理求得∠A=180°﹣∠ABC﹣∠C=70°.
【解答】解:(1)∵DE∥BC,
∴∠2=∠EBC.
又∵∠1=∠2,
∴∠EBC=∠1.
∴FG∥BE.
(2)由(1)得,∠EBC=∠2=30°.
∵BE为∠ABC的角平分线,
∴∠ABC=2∠EBC=60°.
∴∠A=180°﹣∠ABC﹣∠C=70°.
【点评】本题主要考查平行线的性质与判定、角平分线的定义、三角形内角和定理,熟练掌握平行线的性质与判定、角平分线的定义、三角形内角和定理是解决本题的关键.
23.【分析】(1)根据三角形内角和定理求出∠BAC=180°﹣∠B﹣∠C=76°,根据角平分线定义得出∠BAE=∠CAEBAC,即可求出答案;
(2)根据垂直定义得出∠ADC=90°,∠AFD=90°,根据直角三角形的两锐角互余得出∠DAC=90°﹣∠C=20°,求出∠DAE,再根据直角三角形的两锐角互余求出答案即可.
【解答】解:(1)∵∠B=34°,∠C=70°,
∴∠BAC=180°﹣∠B﹣∠C=76°,
∵AE平分∠BAC,
∴∠BAE=∠CAEBAC76°=38°;
(2)∵AD⊥BC,
∴∠ADC=90°,
∵∠C=70°,
∴∠DAC=90°﹣∠C=20°,
∵∠EAC=38°,
∴∠DAE=∠EAC﹣∠DAC=38°﹣20°=18°,
∵DF⊥AE,
∴∠AFD=90°,
∴∠ADF=90°﹣∠DAE=90°﹣18°=72°.
【点评】本题考查了三角形内角和定理,角平分线的定义和直角三角形的性质等知识点,能熟记三角形内角和定理等于180°和直角三角形的两锐角互余是解此题的关键.
24.【分析】(1)由题意可得∠AEC=90°,则由三角形的内角和定理可求得∠BAC=80°,∠CAE=20°,再由角平分线的定义得∠CAD=40°,即可求∠DAE的度数;
(2)由三角形的内角和定理可求得∠BAC=84°,再由角平分线的定义得∠CAD=42°,再由三角形的内角和定理求得∠ADC=70°,由对顶角相等得∠EDF=70°,结合FE⊥BC,即可求解;
(3)由角平分线的定义得∠BAD=∠CAD,∠AEC=∠AED,再由三角形的内角和定理得∠AEC=180°﹣∠C﹣∠CAE,由三角形的外角性质得∠ADE=∠B+∠BAD,再结合∠ADE+∠AED+∠DAE=180°,即可求解.
【解答】解:(1)∵AE⊥BC,
∴∠AEC=90°,
∵∠B=30°,C=70°,
∴∠BAC=180°﹣∠B﹣∠C=80°,
∠CAE=180°﹣∠AEC﹣∠C=20°,
∵AD平分∠BAC,
∴∠CAD∠BAC=40°,
∴∠DAE=∠CAD﹣∠CAE=20°;
(2)∵∠B=28°,∠C=68°,
∴∠BAC=180°﹣∠B﹣∠C=84°,
∵AD平分∠BAC,
∴∠CAD∠BAC=42°,
∴∠ADC=180°﹣∠C﹣∠CAD=70°,
∴∠EDF=∠ADC=70°,
∵FE⊥BC,
∴∠DEF=90°,
∴∠DFE=180°﹣∠DEF﹣∠EDF=20°;
(3)∵AD平分∠BAC,EA平分∠BEC,
∴∠BAD=∠CAD,∠AEC=∠AED,
∵∠AEC=180°﹣∠C﹣∠CAE,∠ADE=∠B+∠BAD,
∠ADE+∠AED+∠DAE=180°,∠CAE=∠CAD﹣∠DAE,
∴∠B+∠BAD+180°﹣∠C﹣∠CAD+∠DAE+∠DAE=180°,
整理得:2∠DAE=∠C﹣∠B,
∵∠C﹣∠B=38°,
∴2∠DAE=38°,
∴∠DAE=19°.
【点评】本题主要考查三角形的内角和定理,解答的关键是结合图形分析清楚各角之间的关系.
25.【分析】(1)根据角平分线的定义,由BP、CP为∠ABC和∠ACB的角平分线,得∠CBP,∠BCP,推断出∠CBP+∠CBP.根据三角形的内角和定理,∠ABC+∠ACB=180°﹣∠A,那么∠PBC+∠PCB,进而推断出∠P=180°﹣(∠PBC+∠PCB)=90°.
(2)根据三角形外角的性质,得∠P=∠PCD﹣∠PBC.根据角平分线的定义,得∠PCD,∠PBC,那么∠P.
(3)根据三角形外角的性质,得∠DBC=∠A+∠ACB,∠BCE=∠A+∠ABC,那么∠DBC+∠BCE=180°+∠A.根据角平分线的定义,BP、CP为∠CBD和∠BCE的角平分线,
得∠CBP,∠BCP,那么,那么∠P=180°﹣(∠CBP+∠BCP)=90°.
【解答】解:(1)∵BP、CP为∠ABC和∠ACB的角平分线,
∴∠CBP,∠BCP.
∴∠CBP+∠CBP.
∵∠A+∠ABC+∠ACB=180°,
∴∠ABC+∠ACB=180°﹣∠A.
∴∠PBC+∠PCB.
∴∠P=180°﹣(∠PBC+∠PCB)=180°90°.
(2)∵∠P+∠PBC=∠PCD,
∴∠P=∠PCD﹣∠PBC.
∵BP、CP为∠ABC和∠ACE的角平分线,
∴∠PCD,∠PBC.
∴∠P.
(3)∵∠DBC=∠A+∠ACB,∠BCE=∠A+∠ABC,
∴∠DBC+∠BCE=∠A+∠ACB+∠A+∠ABC=180°+∠A.
∵BP、CP为∠CBD和∠BCE的角平分线,
∴∠CBP,∠BCP.
∴.
∴∠P=180°﹣(∠CBP+∠BCP)=180°90°.
【点评】本题主要考查角平分线的定义、三角形外角的性质,熟练掌握角平分线的定义以及三角形外角的性质是解决本题的关键.
26.【分析】(1)通过作平行线,利用平行线的性质,将三角形的三个内角“集中”到一个顶点处的邻补角即可;
(2)利用平行线的性质和三角形的内角和定理可得结论;
(3)利用角平分线的定义,三角形的内角和定理以及等腰三角形的判定和性质可得结论.
【解答】解:(1)如图1,延长BC,过点C作CE∥AB,
∵CE∥AB,
∴∠A=∠ACE,∠B=∠DCE,
又∵∠ACB+∠ACE+∠DCE=180°,
∴∠A+∠B+∠ACB=180°;
(2)如图2,
∵BC∥DE.
∴∠ACB=∠EDF,
又∵∠A+∠B+∠ACB=180°=∠E+∠F+∠EDF,
∴∠A+∠B=∠E+∠F;
(3)如图3,
∵AD是∠ABC的角平分线,
∴∠BAD=∠CAD∠BAC,
∵∠EAF=∠EAC+∠CAD,∠ADE=∠BAD+∠B,∠EAC=∠B,
∴∠EAD=∠ADE,
∴EA=ED,
又∵EF⊥AD,
∴∠AEF=∠DEF,
即EF平分∠AED.
【点评】本题考查平行线的性质,角平分线的定义,等腰三角形的判定和性质以及三角形内角和定理,掌握平行线的性质,角平分线的定义,等腰三角形的判定和性质以及三角形内角和定理是正确解答的前提.
27.【分析】(1)由证明过程,结合具体的图形可得答案;
(2)过点A作DE∥BC,利用平行线的性质以及平角的定义可得结论;
(3)在BC边上任取一点D,分别作DE∥AB,DF∥AC,利用平行线的性质和平角的定义可得答案.
【解答】解:(1)故答案为:两直线平行,同位角相等,平角定义;
(2)证明:如图2,过点A作DE∥BC,
∵DE∥BC,
∴∠B=∠BAD,∠C=∠CAE.
∵∠BAD+∠BAC+∠CAE=180°,
∴∠BAC+∠B+∠C=180°;
(3)如图3,过点D作DE∥AB,DF∥AC,
∵DE∥AB,
∴∠B=∠CDE,∠BFD=∠EDF.
∵DF∥AC,
∴∠C=∠BDF,∠BFD=∠A.
∴∠A=∠EDF.
∵∠BDF+∠EDF+∠CDE=180°,
∴∠BAC+∠B+∠C=180°.
【点评】本题考查三角形的内角和定理,掌握平行线的性质以及平角的定义是解决问题的前提.
