2022-2023学年北师大版八年级数学上册4.3 一次函数的图象同步练习(Word版含答案)
文档属性
| 名称 | 2022-2023学年北师大版八年级数学上册4.3 一次函数的图象同步练习(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 470.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-21 09:49:07 | ||
图片预览



文档简介
北师大版八上 4.3 一次函数的图象
一、选择题(共8小题)
1. 如果一个正比例函数 的图象经过不同象限的两点 ,,那么一定有
A. , B. , C. , D. ,
2. 根据下表中 与 的几组对应值画出的函数图象是
A. B.
C. D.
3. 正比例函数 的图象如图所示,则 的值为
A. B. C. D.
4. 下列图象中,表示正比例函数图象的是
A. B.
C. D.
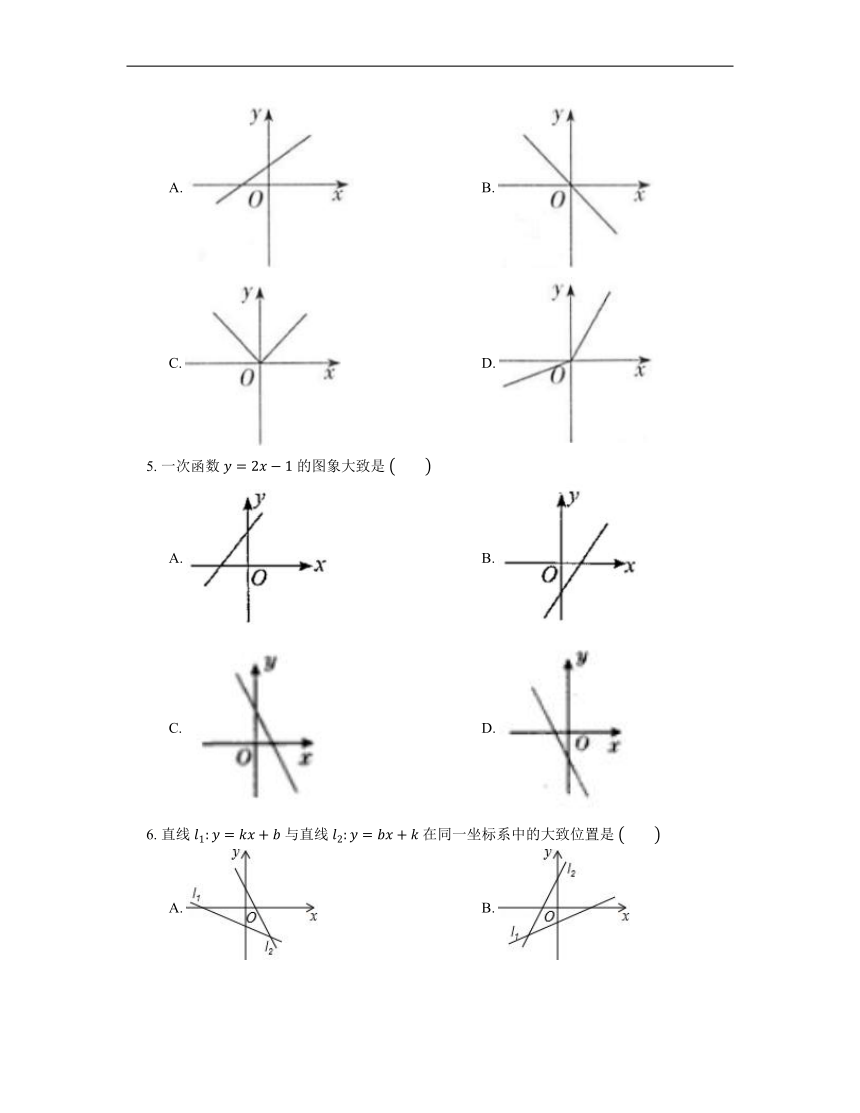
5. 一次函数 的图象大致是
A. B.
C. D.
6. 直线 与直线 在同一坐标系中的大致位置是
A. B.
C. D.
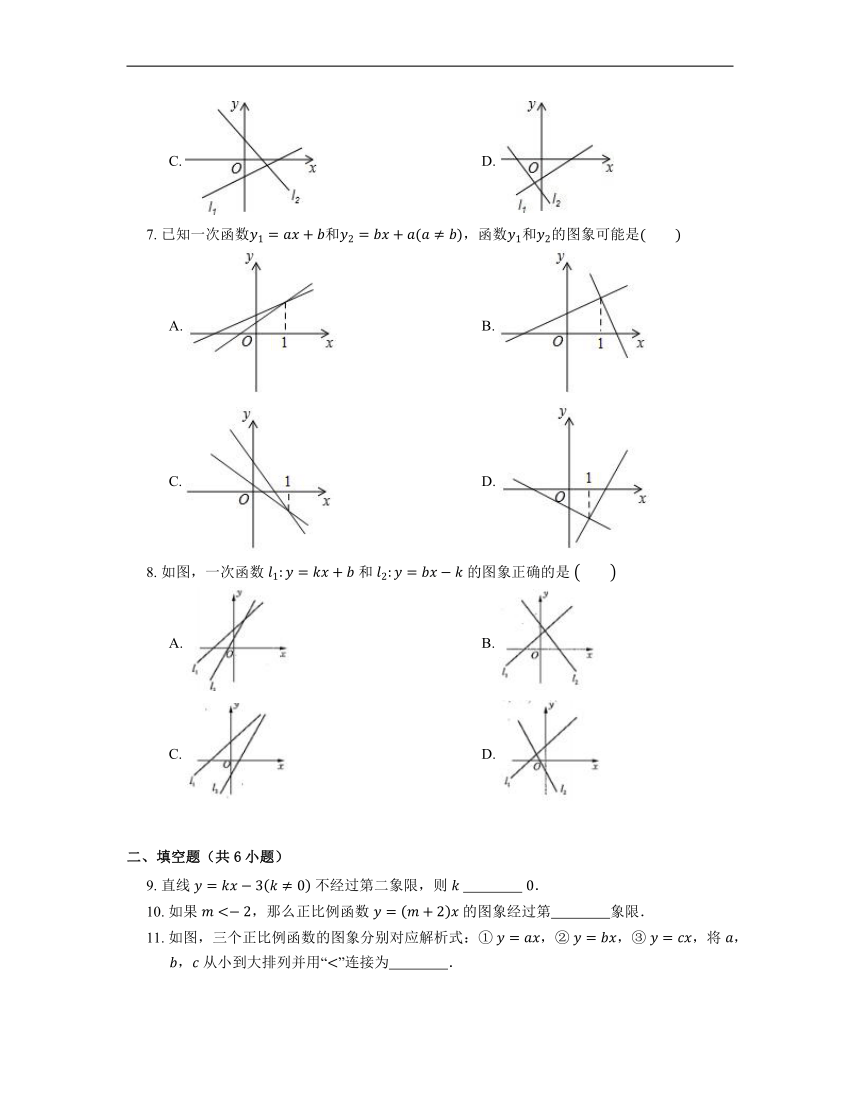
7. 已知一次函数和,函数和的图象可能是
A. B.
C. D.
8. 如图,一次函数 和 的图象正确的是
A. B.
C. D.
二、填空题(共6小题)
9. 直线 不经过第二象限,则 .
10. 如果 ,那么正比例函数 的图象经过第 象限.
11. 如图,三个正比例函数的图象分别对应解析式:① ,② ,③ ,将 ,, 从小到大排列并用“”连接为 .
12. 已知 , 的坐标分别为 ,,点 在直线 上,如果 为等腰三角形,那么这样的点 共有 个.
13. 在右面的平面直角坐标系中作出 与 这两个函数的图象.从而可以得到:函数 与 轴交于点 ,而函数 的图象与 轴交于点 .因此函数 的图象可以看做由直线 向 平移 个单位长度而得到.这样函数 的图象又可称为直线 .
14. 已知 ,,则函数 的图象经过的象限为 象限.
三、解答题(共6小题)
15. 已知 关于 的一次函数解析式是 ( 是常数).分别根据下列条件求 的值或 的取值范围:
(1)函数图象经过第一、二、四象限.
(2)函数图象不经过第三象限.
(3)函数图象既不经过第一象限,又不经过第三象限.
16. 画一次函数 的图象.
某厂生产的 型体重秤,最大称重为 千克,体检时可看到如图①所示的显示盘.已知指针顺时针旋转角 (度)与体重 (千克)有如下关系:
(1)根据表格中的数据在平面直角坐标系(图②)中描出相应的点,顺次连接各点后,你发现这些点在哪一种函数图象上 合理猜想符合这个图象的函数解析式.
(2)验证这些点的坐标是否满足函数解析式,归纳你的结论(写出自变量 的取值范围).
(3)当指针旋转到 度的位置时,显示盘上的体重读数模糊不清,请用解析式求出此时所称的体重.
18. 已知:一次函数 ,求:
(1) 为何值时, 随 的增大而增大
(2) 为何值时,函数图象与 轴的交点在 轴上方
(3) 为何值时,图象不经过第四象限
19. 用你认为简单的方法在坐标系中画出下列函数的图象:
(1);
(2).
20. 在单位“克”与“千克”的换算中, 克是 千克.如果把 克表示为 千克,那么.
(1) 与 之间是否成正比例
(2)写出 关于 的函数解析式,并指出这个函数的定义域.
(3)当 (克)时, 的值是多少(千克)
(4)在直角坐标平面内画出这个函数的图象.
答案
1. B
【解析】正比例函数 的图象经过第一、三象限或第二、四象限.
点 和 在不同象限,
点 在第二象限,点 在第四象限,
,.
2. A
3. B
【解析】由题图知,点 在函数 的图象上,
,解得 ,
故选B.
4. B
【解析】正比例函数图象是过原点的一条直线.
5. B
6. C
【解析】根据一次函数的系数与图象的关系依次分析选项可得:
A.由图可得, 中,,, 中,,, 的取值矛盾,故本选项错误;
B.由图可得, 中,,, 中,,, 的取值相矛盾,故本选项错误;
C.由图可得, 中,,, 中,,,, 的取值相一致,故本选项正确;
D.由图可得, 中,,, 中,,, 的取值相矛盾,故本选项错误.
故选:C.
7. A
【解析】【分析】根据直线①判断出、的符号,然后根据、的符号判断出直线②经过的象限即可,做出判断.
【解析】解:、由①可知:,.
直线②经过一、二、三象限,故正确;
、由①可知:,.
直线②经过一、二、三象限,故错误;
、由①可知:,.
直线②经过一、二、四象限,交点不对,故错误;
、由①可知:,,
直线②经过二、三、四象限,故错误.
故选:.
【点评】本题主要考查的是一次函数的图象和性质,掌握一次函数的图象和性质是解题的关键.
8. C
9.
【解析】 直线 不经过第二象限,则经过一、三、四象限,
.
10. 二,四
【解析】,
,
的图象经过第二,四象限.
故答案为:二,四.
11.
12.
【解析】在坐标系中画出直线 及 , 两点,作 的中垂线,与直线 有 个交点;
以 为圆心、 长为半径画圆,与直线 有 个交点;
以 为圆心、 长为半径画圆,与直线 也有 个交点,
故这样的点 共有 个.
13. 如图即为所求.
,原点,,上,,
14. 一、二、三
15. (1) .
(2) .
(3) .
16.
17. (1) 如图,描点连线后,发现四个点在经过原点的一条直线上,即在正比例函数图象上,猜想 ().
(2) 将 , 代入 ()中,得 ,则 ,因此 .
把 , 代入上面的函数解析式中,
,,,
因此 满足 .
同理可验证 也满足 .
因为最大称重为 千克,
所以将 代入解析式得 ,
解得 ,
因此符合要求的函数解析式是 ().
(3) 当 时,.
答:此时所称的体重是 千克.
18. (1) .
(2) .
(3) .
19. (1) 一次函数 的图象是经过 , 的一条直线;
(2) 一次函数 的图象是经过 , 的一条直线;
如图:
20. (1) , 与 成正比例.
(2)
(3) 当 (克)时,(千克).
(4) 如图所示:
一、选择题(共8小题)
1. 如果一个正比例函数 的图象经过不同象限的两点 ,,那么一定有
A. , B. , C. , D. ,
2. 根据下表中 与 的几组对应值画出的函数图象是
A. B.
C. D.
3. 正比例函数 的图象如图所示,则 的值为
A. B. C. D.
4. 下列图象中,表示正比例函数图象的是
A. B.
C. D.
5. 一次函数 的图象大致是
A. B.
C. D.
6. 直线 与直线 在同一坐标系中的大致位置是
A. B.
C. D.
7. 已知一次函数和,函数和的图象可能是
A. B.
C. D.
8. 如图,一次函数 和 的图象正确的是
A. B.
C. D.
二、填空题(共6小题)
9. 直线 不经过第二象限,则 .
10. 如果 ,那么正比例函数 的图象经过第 象限.
11. 如图,三个正比例函数的图象分别对应解析式:① ,② ,③ ,将 ,, 从小到大排列并用“”连接为 .
12. 已知 , 的坐标分别为 ,,点 在直线 上,如果 为等腰三角形,那么这样的点 共有 个.
13. 在右面的平面直角坐标系中作出 与 这两个函数的图象.从而可以得到:函数 与 轴交于点 ,而函数 的图象与 轴交于点 .因此函数 的图象可以看做由直线 向 平移 个单位长度而得到.这样函数 的图象又可称为直线 .
14. 已知 ,,则函数 的图象经过的象限为 象限.
三、解答题(共6小题)
15. 已知 关于 的一次函数解析式是 ( 是常数).分别根据下列条件求 的值或 的取值范围:
(1)函数图象经过第一、二、四象限.
(2)函数图象不经过第三象限.
(3)函数图象既不经过第一象限,又不经过第三象限.
16. 画一次函数 的图象.
某厂生产的 型体重秤,最大称重为 千克,体检时可看到如图①所示的显示盘.已知指针顺时针旋转角 (度)与体重 (千克)有如下关系:
(1)根据表格中的数据在平面直角坐标系(图②)中描出相应的点,顺次连接各点后,你发现这些点在哪一种函数图象上 合理猜想符合这个图象的函数解析式.
(2)验证这些点的坐标是否满足函数解析式,归纳你的结论(写出自变量 的取值范围).
(3)当指针旋转到 度的位置时,显示盘上的体重读数模糊不清,请用解析式求出此时所称的体重.
18. 已知:一次函数 ,求:
(1) 为何值时, 随 的增大而增大
(2) 为何值时,函数图象与 轴的交点在 轴上方
(3) 为何值时,图象不经过第四象限
19. 用你认为简单的方法在坐标系中画出下列函数的图象:
(1);
(2).
20. 在单位“克”与“千克”的换算中, 克是 千克.如果把 克表示为 千克,那么.
(1) 与 之间是否成正比例
(2)写出 关于 的函数解析式,并指出这个函数的定义域.
(3)当 (克)时, 的值是多少(千克)
(4)在直角坐标平面内画出这个函数的图象.
答案
1. B
【解析】正比例函数 的图象经过第一、三象限或第二、四象限.
点 和 在不同象限,
点 在第二象限,点 在第四象限,
,.
2. A
3. B
【解析】由题图知,点 在函数 的图象上,
,解得 ,
故选B.
4. B
【解析】正比例函数图象是过原点的一条直线.
5. B
6. C
【解析】根据一次函数的系数与图象的关系依次分析选项可得:
A.由图可得, 中,,, 中,,, 的取值矛盾,故本选项错误;
B.由图可得, 中,,, 中,,, 的取值相矛盾,故本选项错误;
C.由图可得, 中,,, 中,,,, 的取值相一致,故本选项正确;
D.由图可得, 中,,, 中,,, 的取值相矛盾,故本选项错误.
故选:C.
7. A
【解析】【分析】根据直线①判断出、的符号,然后根据、的符号判断出直线②经过的象限即可,做出判断.
【解析】解:、由①可知:,.
直线②经过一、二、三象限,故正确;
、由①可知:,.
直线②经过一、二、三象限,故错误;
、由①可知:,.
直线②经过一、二、四象限,交点不对,故错误;
、由①可知:,,
直线②经过二、三、四象限,故错误.
故选:.
【点评】本题主要考查的是一次函数的图象和性质,掌握一次函数的图象和性质是解题的关键.
8. C
9.
【解析】 直线 不经过第二象限,则经过一、三、四象限,
.
10. 二,四
【解析】,
,
的图象经过第二,四象限.
故答案为:二,四.
11.
12.
【解析】在坐标系中画出直线 及 , 两点,作 的中垂线,与直线 有 个交点;
以 为圆心、 长为半径画圆,与直线 有 个交点;
以 为圆心、 长为半径画圆,与直线 也有 个交点,
故这样的点 共有 个.
13. 如图即为所求.
,原点,,上,,
14. 一、二、三
15. (1) .
(2) .
(3) .
16.
17. (1) 如图,描点连线后,发现四个点在经过原点的一条直线上,即在正比例函数图象上,猜想 ().
(2) 将 , 代入 ()中,得 ,则 ,因此 .
把 , 代入上面的函数解析式中,
,,,
因此 满足 .
同理可验证 也满足 .
因为最大称重为 千克,
所以将 代入解析式得 ,
解得 ,
因此符合要求的函数解析式是 ().
(3) 当 时,.
答:此时所称的体重是 千克.
18. (1) .
(2) .
(3) .
19. (1) 一次函数 的图象是经过 , 的一条直线;
(2) 一次函数 的图象是经过 , 的一条直线;
如图:
20. (1) , 与 成正比例.
(2)
(3) 当 (克)时,(千克).
(4) 如图所示:
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
