2022-2023学年北师大版九年级数学上册 4.5相似三角形判定定理的证明 解答专项练习题(Word版含答案)
文档属性
| 名称 | 2022-2023学年北师大版九年级数学上册 4.5相似三角形判定定理的证明 解答专项练习题(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 683.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-22 00:00:00 | ||
图片预览



文档简介
2022-2023学年北师大版九年级数学上册《4.5相似三角形判定定理的证明》
解答专项练习题(附答案)
1.如图,在△ABC中,点D,E分别在边AB,AC上,且BE平分∠ABC,∠ABE=∠ACD,BE,CD交于点G.
(1)求证:=;
(2)连接DE,求证:DE=CE;
(3)若CD⊥AB,AD=2,BD=3,求线段EG的长.
2.如图,在Rt△ABC中,AC=4,∠BAC=90°,∠B=30°,D是BC上一点,AE⊥AD,∠ADE=30°,连接CE.
(1)求证:△ADE∽△ABC;
(2)求证:△ACE∽△ABD;
(3)设CE=x,当CD=2CE时,求x的值.
3.如图,在△ABC中,AG⊥BC,垂足为点G,点E为边AC上一点,BE=CE,点D为边BC上一点,GD=GB,连接AD交BE于点F.
(1)求证:∠ABE=∠EAF;
(2)求证:AE2=EF EC;
(3)若CG=2AG,AD=2AF,BC=5,求AE的长.
4.如图,E是矩形ABCD的边BC上的一点,AC是其对角线,连接AE,过点E作EF⊥AE,EF交AC于点M,EF交DC于点F,过点B作BG⊥AC于点G,BG交AE于点H.
(1)求证:△ABE∽△ECF;
(2)求证:AH CM=BH EM;
(3)若E是BC的中点,=,AB=6,求EM的长.
5.如图,△ABC中,DE∥BC,G是AE上一点,连接BG交DE于F,作GH∥AB交DE于点H.
(1)如图1,与△GHE相似的三角形是 (直接写出答案);
(2)如图1,若AD=3BD,BF=FG,求的值;
(3)如图2,连接CH并延长交AB于P点,交BG于Q,连接PF,则一定有PF∥CE,请说明理由.
6.如图,在Rt△ABC中,∠C=90°,AD平分∠BAC交BC于点D,DE⊥AD交AB于E,EF∥BC交AC于F.
(1)求证:△ACD∽△ADE;
(2)求证:AD2=AB AF;
(3)作DG⊥BC交AB于G,连接FG,若FG=5,BE=8,直接写出AD的长.
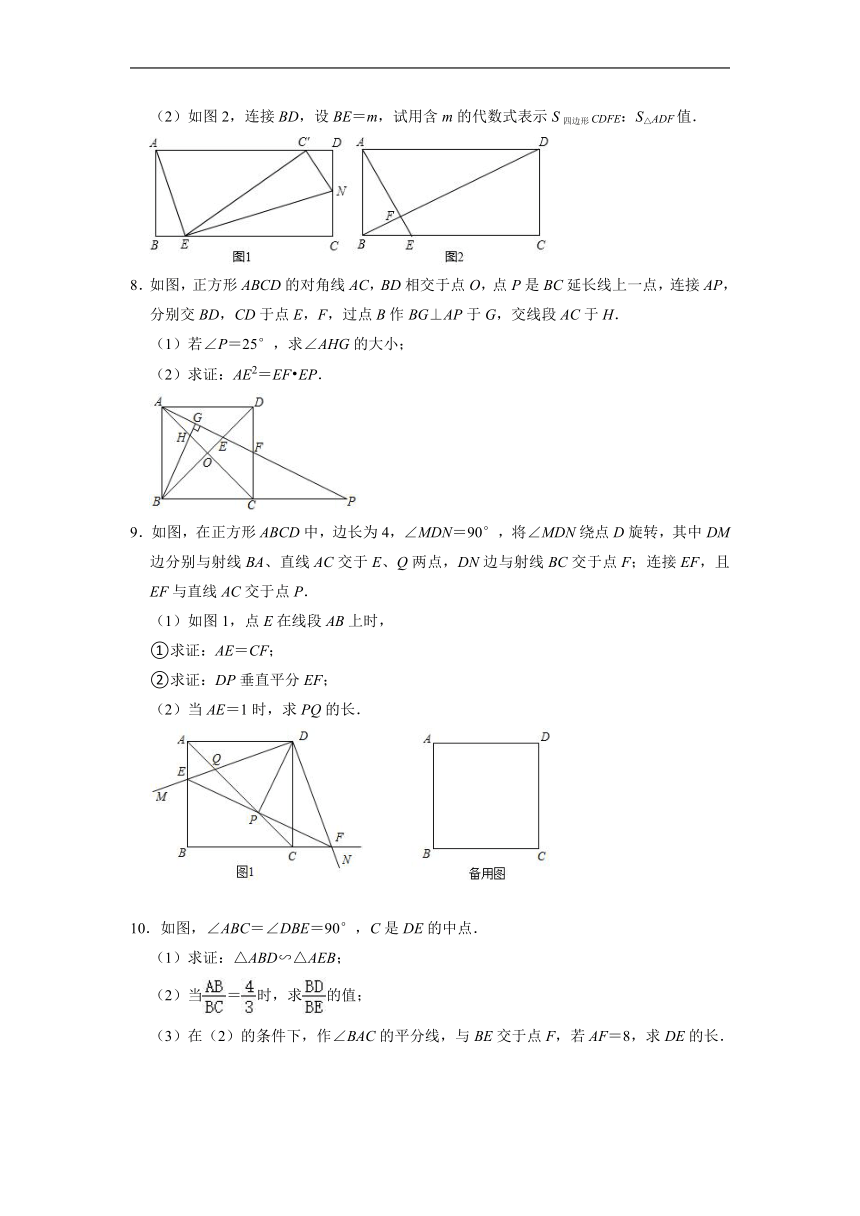
7.已知四边形ABCD是矩形,AB=2,BC=4,E为BC边上一动点且不与B、C重合,连接AE(1)如图1,过点E作EN⊥AE交CD于点N.
①若BE=1,求CN的长;
②将△ECN沿EN翻折,点C恰好落在边AD上,求BE的长;
(2)如图2,连接BD,设BE=m,试用含m的代数式表示S四边形CDFE:S△ADF值.
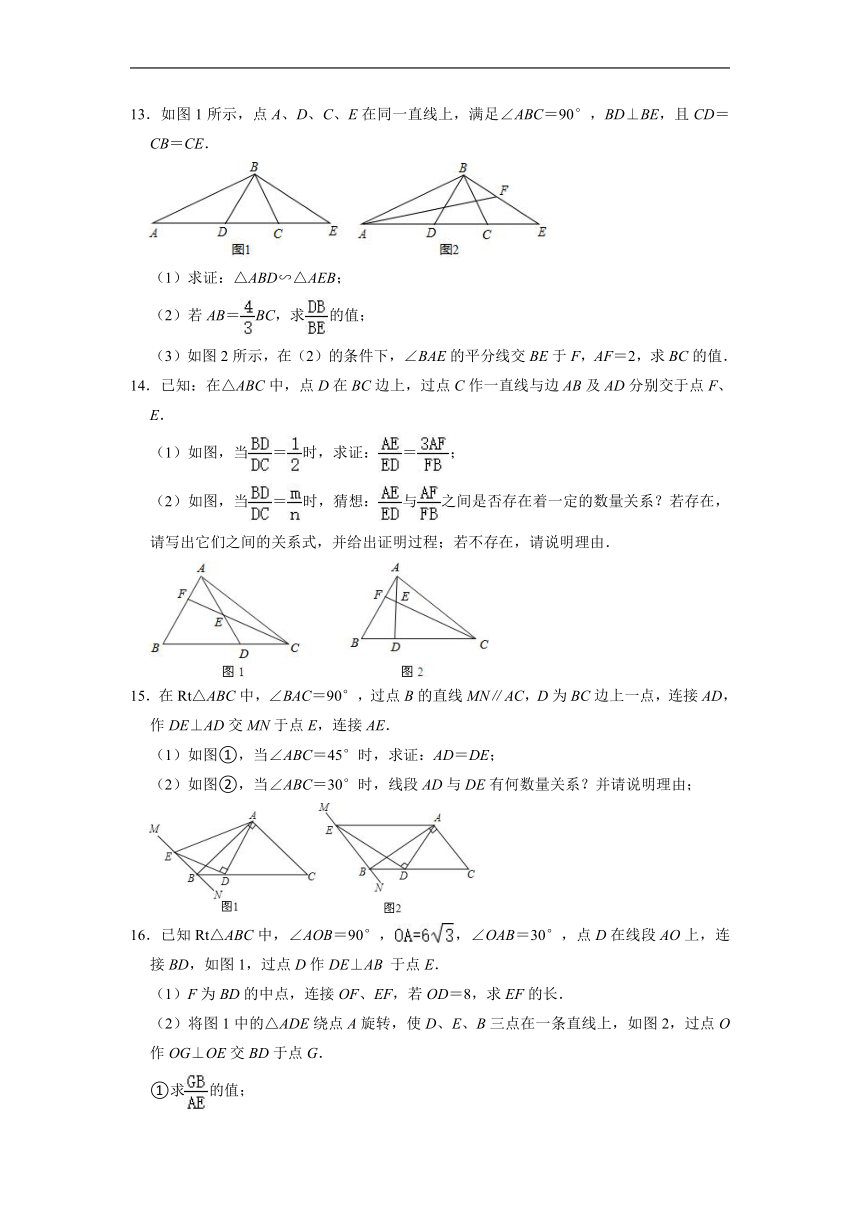
8.如图,正方形ABCD的对角线AC,BD相交于点O,点P是BC延长线上一点,连接AP,分别交BD,CD于点E,F,过点B作BG⊥AP于G,交线段AC于H.
(1)若∠P=25°,求∠AHG的大小;
(2)求证:AE2=EF EP.
9.如图,在正方形ABCD中,边长为4,∠MDN=90°,将∠MDN绕点D旋转,其中DM边分别与射线BA、直线AC交于E、Q两点,DN边与射线BC交于点F;连接EF,且EF与直线AC交于点P.
(1)如图1,点E在线段AB上时,
①求证:AE=CF;
②求证:DP垂直平分EF;
(2)当AE=1时,求PQ的长.
10.如图,∠ABC=∠DBE=90°,C是DE的中点.
(1)求证:△ABD∽△AEB;
(2)当=时,求的值;
(3)在(2)的条件下,作∠BAC的平分线,与BE交于点F,若AF=8,求DE的长.
11.如图,已知:正方形ABCD,点E在CB的延长线上,连接AE、DE,DE与边AB交于点F,FG∥BE交AE于点G.
(1)求证:GF=BF;
(2)若EB=1,BC=4,求AG的长;
(3)在BC边上取点M,使得BM=BE,连接AM交DE于点O.求证:FO ED=OD EF.
12.阅读下面材料:小昊遇到这样一个问题:如图1,在△ABC中,BE是AC边上的中线,点D在BC边上,=,AD与BE相交于点P,求的值.
小昊发现,过点C作CF∥AD,交BE的延长线于点F,通过构造△CEF,经过推理和计算能够使问题得到解决(如图2).
请回答:的值为 .
参考小昊思考问题的方法,解决问题:
(1)如图3,在△ABC中,点D在BC的延长线上,,点E在AC上,且.求的值;
(2)如图4,在△ABC中,点D在BC的延长线上,,点E在AC上,且,直接写出的值为 .
13.如图1所示,点A、D、C、E在同一直线上,满足∠ABC=90°,BD⊥BE,且CD=CB=CE.
(1)求证:△ABD∽△AEB;
(2)若AB=BC,求的值;
(3)如图2所示,在(2)的条件下,∠BAE的平分线交BE于F,AF=2,求BC的值.
14.已知:在△ABC中,点D在BC边上,过点C作一直线与边AB及AD分别交于点F、E.
(1)如图,当=时,求证:=;
(2)如图,当=时,猜想:与之间是否存在着一定的数量关系?若存在,请写出它们之间的关系式,并给出证明过程;若不存在,请说明理由.
15.在Rt△ABC中,∠BAC=90°,过点B的直线MN∥AC,D为BC边上一点,连接AD,作DE⊥AD交MN于点E,连接AE.
(1)如图①,当∠ABC=45°时,求证:AD=DE;
(2)如图②,当∠ABC=30°时,线段AD与DE有何数量关系?并请说明理由;
16.已知Rt△ABC中,∠AOB=90°,,∠OAB=30°,点D在线段AO上,连接BD,如图1,过点D作DE⊥AB 于点E.
(1)F为BD的中点,连接OF、EF,若OD=8,求EF的长.
(2)将图1中的△ADE绕点A旋转,使D、E、B三点在一条直线上,如图2,过点O作OG⊥OE交BD于点G.
①求的值;
②若点F为线段BD的中点,,直接写出线段OF的长度.
17.已知:在正方形ABCD中,E为BC延长线上一点,连接AE分别交DC、DB于F、G.求证:
(1)∠DAG=∠DCG;
(2)AG2=GE GF;
(3)已知,,求该正方形的边长.
18.在锐角△ABC中,AB=4,BC=5,∠ACB=45°,将△ABC绕点B按逆时针方向旋转,得到△A1BC1.
(1)如图1,当点C1在线段CA的延长线上时,求∠CC1A1的度数;
(2)如图2,连接AA1,CC1.若△ABA1的面积为4,求△CBC1的面积;
(3)如图3,点E为线段AB中点,点P是线段AC上的动点,在△ABC绕点B按逆时针方向旋转过程中,点P的对应点是点P1,求线段EP1长度的最大值与最小值.
19.在矩形ABCD中,AB=4,BC=3,E是AB边上一点,EF⊥CE交AD于点F,过点E作∠AEH=∠BEC,交射线FD于点H,交射线CD于点N.
(1)如图a,当点H与点F重合时,求BE的长;
(2)如图b,当点H在线段FD上时,设BE=x,DN=y,求y与x之间的函数关系式,并写出它的定义域;
(3)连接AC,当△FHE与△AEC相似时,求线段DN的长.
20.如图,∠ACB=90°,CD⊥AB,垂足为D,点E在AC上,BE交CD于点G,EF⊥BE交AB于点F.
(1)如图①,若AC=BC,CE=EA,探索线段EF与EG的数量关系,并证明你的结论;
(2)如图②,若AC=mBC,CE=kEA,探索线段EF与EG的数量关系,并证明你的结论.
参考答案
1.证明:(1)∵∠ABE=∠ACD,∠A=∠A,
∴△ABE∽△ACD,
∴;
(2)∵,
∴,
又∵∠A=∠A,
∴△ADE∽△ACB,
∴∠AED=∠ABC,
∵∠AED=∠ACD+∠CDE,∠ABC=∠ABE+∠CBE,
∴∠ACD+∠CDE=∠ABE+∠CBE,
∵∠ABE=∠ACD,
∴∠CDE=∠CBE,
∵BE平分∠ABC,
∴∠ABE=∠CBE,
∴∠CDE=∠ABE=∠ACD,
∴DE=CE;
(3)∵CD⊥AB,
∴∠ADC=∠BDC=90°,
∴∠A+∠ACD=∠CDE+∠ADE=90°,
∵∠ABE=∠ACD,∠CDE=∠ACD,
∴∠A=∠ADE,∠BEC=∠ABE+∠A=∠A+∠ACD=90°,
∴AE=DE,BE⊥AC,
∵DE=CE,
∴AE=DE=CE,
∴AB=BC,
∵AD=2,BD=3,
∴BC=AB=AD+BD=5,
在Rt△BDC中,CD===4,
在Rt△ADC中,AC===2,
∴DE=AE=CE=,
∵∠ADC=∠GEC=90°,∠ACD=∠GCE,
∴△CGE∽△CAD,
∴,
∴GE===.
2.(1)证明:∵AE⊥AD,∠BAC=90°,
∴∠EAD=∠CAB=90°,
∵∠B=30°,∠ADE=30°,
∴∠B=∠ADE,
∴△ADE∽△ABC;
(2)证明:∵∠EAD=∠CAB=90°,
∴∠EAC=∠DAB=90°﹣∠CAD,
∵△ADE∽△ABC,
∴=,
∴=,
∴△ACE∽△ABD;
(3)解:在Rt△ABC中,∠CAB=90°,AC=4,∠B=30°,
∴BC=2AC=8,AB===4,
∵CE=x,CD=2CE,
∴CD=2x,
∵△ACE∽△ABD,
∴=,
∴=,
∴BD=x,
∴BC=CD+BD=2x+x=8,
解得:x=16﹣8.
3.(1)证明:∵EB=EC,
∴∠EBC=∠C,
∵AG⊥BD,BG=GD,
∴AB=AD,
∴∠ABD=∠ADB,
∵∠ABD=∠ABE+∠EBC,∠ADB=∠DAC+∠C,
∴∠ABE=∠DAC,
即∠ABE=∠EAF.
(2)证明:∵∠AEF=∠BEA,∠EAF=∠ABE,
∴△AEF∽△BEA,
∴=,
∴AE2=EF EB,
∵EB=EC,
∴AE2=EF EC.
(3)解:设BE交AG于J,连接DJ,DE.
∵AG垂直平分线段BD,
∴JB=JD,
∴∠JBD=∠JDG,
∵∠JBD=∠C,
∴∠JDB=∠C,
∴DJ∥AC,
∴∠AEF=∠DJF,
∵AF=DF,∠AFE=∠DFJ,
∴△AFE≌△DFJ(AAS),
∴EF=FJ,AE=DJ,
∵AF=DF,
∴四边形AJDE是平行四边形,
∴DE∥AG,
∵AG⊥BC,
∴ED⊥BC,
∵EB=EC,
∴BD=DC=,
∴BG=DG=,
∵tan∠JDG=tan∠C===,
∴JG=,
∵∠JGD=90°,
∴DJ===,
∴AE=DJ=.
4.(1)证明:∵四边形ABCD是矩形,
∴∠ABE=∠ECF=90°.
∵AE⊥EF,∠AEB+∠FEC=90°.
∴∠AEB+∠BAE=90°,
∴∠BAE=∠CEF,
∴△ABE∽△ECF;
(2)证明:∵BG⊥AC,
∴∠ABG+∠BAG=90°,
∴∠ABH=∠ECM,
由(1)知,∠BAH=∠CEM,
∴△ABH∽△ECM;,
∴=,
∴AH CM=BH EM;
(3)解:作MR⊥BC,垂足为R,
∵=,AB=6,
∴BC=8,
∵E是BC的中点,
∴BE=EC=4,
∵△ABE∽△ECF,
∴=,即=
∴CF=,
∵CD∥RM∥AB,
∴△ERM∽△ECF,△CRM∽△CBA,
∴=,=,即=,=,
∴RM=,
∵=,
∴=,
∴=,
∵△ABE∽△ECF,
∴==,
∴==,
∴EM=RM=×=.
5.(1)解:如图1中,
∵GH∥AD,
∴△GHE∽△ADE,
∵DE∥BC,
∴△ADE∽△ABC,
∴△GHE∽△ADE∽△ABC,
故答案为△ADE,△ABC.
(2)解:∵GH∥BD,
∴∠FGH∠DBF,
∵BF=FG,∠DFB=∠GFH,
∴△BFD≌△GFH(ASA),
∴BD=GH,
∵GH∥AD,
∴===,
∴=.
(3)证明:如图2中,
∵GH∥BD,
∴=,
∵GH∥PA,
∴=,
∵DH∥BC,
∴=,
∴=,
∴=,
∴=,
∴PF∥AG,即PF∥AC.
6.(1)证明:∵DA平分∠BAC,
∴∠CAD=∠DAE,
∵DE⊥AD,
∴∠ADE=∠C=90°,
∴△ACD∽△ADE.
(2)证明:连接DF.
∵EF∥BC,
∴∠AFE=∠C=90°,∠AEF=∠B,
∵∠ADE=∠AFE=90°,
∴A,E,D,F四点共圆,
∴∠ADF=∠AEF,
∴∠B=∠ADF,
∴∠DAB=∠DAF,
∴△BAD∽△DAF,
∴=,
∴AD2=AB AF.
(3)解:设DG交EF于O.
∵DG⊥BC,AC⊥BC,
∴DG∥AC,
∴∠ADG=∠DAC=∠DAG,
∴AG=GD,
∵∠AED+∠EAD=90°,∠EDG+∠ADG=90°,
∴∠GED=∠GDE,
∴DG=EG=AG,
∵∠AFE=90°,
∴FG=EG=AG=DG=5,
∵OE∥BD,
∴=,
∴=,
∴OG=,
∴OG∥AF.EG=AG,
∴OE=OF,
∴AF=2OG=,
∴AD2=AB AF=18×,
∵AD>0,
∴AD=.
7.解:(1)①∵BE=1,
∴CE=BC﹣BE=4﹣1=3,
∵四边形ABCD是矩形,
∴∠B=∠C=90°,
∴∠BAE+∠BEA=90°,
∵EF⊥AE,
∴∠AEF=90°,
∴∠BEA+∠FEC=90°,
∴∠BAE=∠FEC,
∴△ABE∽△ECN,
∴=,
即:=,
解得:CN=;
②过点E作EF⊥AD于F,如图1所示:
则四边形ABEF是矩形,
∴AB=EF=2,AF=BE,
由折叠的性质得:CE=C′E,CN=C′N,∠EC′N=∠C=90°,
∴∠NC′D+∠EC′F=90°,
∵∠C′ND+∠NC′D=90°,
∴∠EC′F=∠C′ND,
∵∠D=∠EFC′,
∴△EC′F∽△NC′D,
∴==,
∴==,
∵=,
∴=,
∴==,
∴C′D=BE,
设BE=x,则C′D=AF=x,C′F=4﹣2x,CE=4﹣x,
∴=,=,
∴DN=x(2﹣x),CN=,
∴CN+DN=x(2﹣x)+=CD=2,
解得:x=2或x=,
∴BE=2或BE=;
(2)∵四边形ABCD为矩形,
∴BC=AD,AD∥BC,
∴△ADF∽△EBF,
∴==,
∴=()2=,
∴S△ADF=s△BEF,
S△ABF===S△BEF,
S四边形CDFE=S△ADF+S△ABF﹣S△BEF=S△BEF+S△BEF﹣S△BEF=(+﹣1)S△BEF,
∴S四边形CDFE:S△ADF=(+﹣1)S△BEF:s△BEF=1+﹣.
8.(1)解:∵四边形ABCD是正方形,
∴∠ACB=45°,
∵∠ACB=∠P+∠CAP,
∴∠CAP=20°,
∵BG⊥AP,
∴∠AGH=90°,
∴AHG=90°﹣20°=70°.
(2)证明:∵四边形ABCD是正方形,
∴A,C关于BD对称,∠ACB=∠ACD=45°,
∴EA=EC,
∴∠EAC=∠ECA,
∵∠ACB=∠P+∠CAE=45°,∠ECF+∠ECA=45°,
∴∠ECF=∠P,
∵∠CEF=∠PEC,
∴△CEF∽△PEC,
∴=,
∴EC2=EF EP,
∴EA2=EF EP.
9.(1)①证明:∵四边形ABCD是正方形,
∴DA=DC,∠ADC=∠DAE=∠DCF=90°,
∴∠ADC=∠MDN=90°,
∴∠ADE=∠CDF,
∴△ADE≌△CDF(ASA),
∴AE=CF.
②∵△ADE≌△CDF(ASA),
∴DE=DF,∵∠MDN=90°,
∴∠DEF=45°,
∵∠DAC=45°,
∴∠DAQ=∠PEQ,∵∠AQD=∠EQP,
∴△AQD∽△EQP,
∴=,
∴=,∵∠AQE=∠PQD,
∴△AQE∽△DQP,
∴∠QDP=∠QAE=45°,
∴∠DPE=90°,
∴DP⊥EF,∵DE=DF,
∴PE=PF,
∴DP垂直平分线段EF.
(2)解:①当点E在线段AB上时,作QH⊥AD于H,QG⊥AB于G.
在Rt△ADE中,DE==,
∵∠QAH=∠QAG=45°,
∴HQ=QG=AH=AG,设QH=x,
∵×4×x+×1×x=×1×4,
∵x=,
∴AQ=,DQ==,EQ=,
∵△AQD∽△EQP,
∴AQ PQ=DQ EQ,
∴PQ==.
②当点E在BA的延长线上时,作QH⊥AD于H,QG⊥AB于G.
在Rt△ADE中,DE==,
∵∠QAH=∠QAG=45°,
∴HQ=QG=AH=AG,设QH=x,
∵×4×x﹣×1×x=×1×4,
∵x=,
∴AQ=,DQ==,EQ=,
∵△AQD∽△EQP,
∴AQ PQ=DQ EQ,
∴PQ==.
综上所述,PQ的长为或.
10.解:(1)证明:∵∠ABC=∠DBE=90°,
∴∠ABD+∠CBD=90°,
∵∠DBE=90°,C是DE的中点.
∴BC=CD=CE,
∴∠E=∠CBE.
∵∠CBE+∠CBD=90°,∠ABD+∠CBD=90°,
∴∠CBE=∠ABD,
∴∠E=∠ABD,
又∵∠BAD=∠EAB,
∴△ABD∽△AEB;
(2)∵=,
∴设AB=4,BC=3,
∴AC==5,
∵BC=CD=3,
∴AD=AC﹣CD=5﹣3=2,
由(1)可知:△ABD∽△AEB,
∴==,
∴AB2=AD AE,
∴42=2AE,
∴AE=8,
∴===;
∴的值为;
(3)过点F作FG⊥AE于点G,
∵=,
∴设AB=4x,BC=3x,
由(2)可知:AE=8x,AD=2x,
∴DE=AE﹣AD=6x,
∵AF平分∠BAC,
∴=,
∴==,
∵tanE==,
∴cosE=,sinE=,
∴=,
∴BE=x,
∴EF=BE=x,
∴sinE==,
∴FG=x,
∵tanE=,
∴GE=2GF=x,
∴AG=AE﹣GE=x,
∵AF2=AG2+GF2,AF=8,
∴64=+,
∴x=,
∴DE=6x=3.
∴DE的长为3.
11.证明:(1)∵四边形ABCD是正方形,
∴AD∥BC,AB∥CD,AD=CD,
∵GF∥BE,
∴GF∥BC,
∴GF∥AD,
∴,
∵AB∥CD,
,
∵AD=CD,
∴GF=BF;
(2)∵EB=1,BC=4,
∴=4,AE=,
∴==4,
∴AG=;
(3)延长GF交AM于H,∵GF∥BC,
∴FH∥BC
∴=,
∴=,
∵BM=BE,
∴GF=FH,
∵GF∥AD,
∴,,
∴,
∴=,
∴FO ED=OD EF.
12.解:如图2,过点C作CF∥AD,交BE的延长线于点F,
∴∠F=∠APF,∠FCE=∠EAP,
∵BE为AC边的中线,
∴AE=CE,
∴△AEP≌△CEF(AAS),
∴AP=FC,
∵PD∥FC,
∴△BPD∽△BFC,
∴=,
∴=,
故答案为:;
(1)如图3,过A作AF∥BC,交BP延长线于点F,
∴△AFE∽△CBE,
∴,
∵,
∴,
设AF=3x,BC=2x,
∵,
∴BD=3x,
∴AF=BD=3x,
∵AF∥BD,
∴△AFP∽△DBP,
∴==1;
(2)如图4,过C作CF∥AP交PB于F,
∴△BCF∽△BDP,
∴,
设CF=2x,PD=3x,
∵CF∥AP,
∴△ECF∽△EAP,
∴,
∴AP=7x,AD=4x,
∴.
故答案为:.
13.解:(1)∵∠ABC=90°,∠DBE=90°,
∴∠ABD=∠CBE,
∵BC=CE,
∴∠CBE=∠E,
∴∠ABD=∠E,
∵∠A=∠A,
∴△ABD∽△AEB;
(2)∵AB:BC=4:3,
∴设AB=4,BC=3,
∴AC==5,
∵BC=CD=3,
∴AD=AC﹣CD=5﹣3=2,
由(1)可知:△ABD∽△AEB,
∴==,
∴AB2=AD AE,
∴42=2AE,
∴AE=8,
在Rt△DBE中
===;
(3)过点F作FM⊥AE于点M,
∵AB:BC=4:3,
∴设AB=4x,BC=3x,
∴由(2)可知;AE=8x,AD=2x,
∴DE=AE﹣AD=6x,
作FN⊥AB,交AB延长线于点N,作AP⊥EB,交EB于点P,
∴S△ABF=AB FN=BF AP,S△AEF=EF AP=AE FM,
∵AF平分∠BAC,
∴FN=FM,
∴==,
∴==,
∴=,
∴BE=x,
∴EF=BE=x,
∴MF=x,
∴ME=2MF=x,
∴AM=AE﹣ME=x,
∵AF2=AM2+MF2,
∴4=(x)2+(x)2,
∴x=,
BC=3x=.
14.解:(1)如图1,过D作DG∥FC交AB于G,
∴=,
∴FB,
∵EF∥DG
∴;
(2)猜想,
证明:如图2,过D作DG∥FC交AB于G,
∴,
∴FG=,
∴=.
15.(1)证明:如图1,过点D作DF⊥BC,交AB于点F,
则∠BDE+∠FDE=90°,
∵DE⊥AD,
∴∠FDE+∠ADF=90°,
∴∠BDE=∠ADF,
∵∠BAC=90°,∠ABC=45°,
∴∠C=45°,
∵MN∥AC,
∴∠EBD=180°﹣∠C=135°,
∵∠BFD=45°,DF⊥BC,
∴∠BFD=45°,BD=DF,
∴∠AFD=135°,
∴∠EBD=∠AFD,
在△BDE和△FDA中
,
∴△BDE≌△FDA(ASA),
∴AD=DE;
(2)解:DE=AD,
理由:如图2,过点D作DG⊥BC,交AB于点G,
则∠BDE+∠GDE=90°,
∵DE⊥AD,
∴∠GDE+∠ADG=90°,
∴∠BDE=∠ADG,
∵∠BAC=90°,∠ABC=30°,
∴∠C=60°,
∵MN∥AC,
∴∠EBD=180°﹣∠C=120°,
∵∠ABC=30°,DG⊥BC,
∴∠BGD=60°,
∴∠AGD=120°,
∴∠EBD=∠AGD,
∴△BDE∽△GDA,
∴=,
在Rt△BDG中,
=,
∴DE=AD;
16.解:(1)在Rt△ABC中,∠AOB=90°,,∠OAB=30°,
∴OB=6,AB=12,
在Rt△OBD中,∵OD=8,
∴BD==10,
∵DE⊥AB,
∴∠DEB=90°,
∴EF=BD=5;
(2)①∵∠AOB=90°,
∵OG⊥OE,
∴∠EOG=90°,
∴∠AOB﹣∠AOG=∠EOG﹣∠AOG,
∴∠AOE=∠BOG,
∵∠AEG+∠OEG=∠EOG+∠OEG,
∴∠AEO=∠OGB,
∴△AEO∽△OGB,
∴==;
②在Rt△ADE中,∵∠DAE=30°,AD=2,
∴AE=3,DE=,
∵=;
∴BG=,
∴DE=BG,
∵点F为线段BD的中点,
∴点F为线段EG的中点,
在Rt△AEB中,
BE==3,
∴EG=3﹣,
∴OF=EG=.
17.(1)证明:∵四边形ABCD是正方形,
∴AD=BC,∠ADG=∠CDG=45°,
在△ADG和△CDG中,
,
∴△ADG≌△CDG(SAS),
∴∠DAG=∠DCG;
(2)∵AD∥BE,
∴∠DAG=∠E,
∵△ADG≌△CDG,
∴∠DAG=∠GCD,AG=CG,
∴∠GCD=∠E,
∵∠GCE=∠GCD+90°,∠GFC=∠DAG+90°,
∴∠GFC=∠GCE,
∴△GCF∽△GEC,
∴CG2=GE GF,
∴AG2=GE GF;
(3)∵,,
∴GE=GF+EF=3﹣3,
∵CG2=GE GF,
∴CG=3﹣,
∴GF:CG=CF:CE=1:,
∵EF=2﹣2,
∴CF=﹣1,CE=3﹣3,
∵CF∥AB,
∴△EFC∽△EAB,
∴,
∴,
解得:AB=.
18.解:(1)由旋转的性质可得:∠A1C1B=∠ACB=45°,BC=BC1,
∴∠CC1B=∠C1CB=45°,
∴∠CC1A1=∠CC1B+∠A1C1B=45°+45°=90°.
(2)∵△ABC≌△A1BC1,
∴BA=BA1,BC=BC1,∠ABC=∠A1BC1,
∴,∠ABC+∠ABC1=∠A1BC1+∠ABC1,
∴∠ABA1=∠CBC1,
∴△ABA1∽△CBC1.
∴,
∵S△ABA1=4,
∴S△CBC1=;
(3)①如图1,过点B作BD⊥AC,D为垂足,
∵△ABC为锐角三角形,
∴点D在线段AC上,
在Rt△BCD中,BD=BC×sin45°=,
当P在AC上运动,BP与AC垂直的时候,△ABC绕点B旋转,使点P的对应点P1在线段AB上时,EP1最小,最小值为:EP1=BP1﹣BE=BD﹣BE=﹣2;
②当P在AC上运动至点C,△ABC绕点B旋转,使点P的对应点P1在线段AB的延长线上时,EP1最大,最大值为:EP1=BC+BE=2+5=7.
19.解:(1)∵EF⊥EC,
∴∠AEF+∠BEC=90°,
∵∠AEF=∠BEC,
∴∠AEF=∠BEC=45°,
∵∠B=90°,
∴BE=BC,
∵BC=3,
∴BE=3;
(2)过点E作EG⊥CN,垂足为点G,
∴四边形BEGC是矩形,
∴BE=CG,
∵AB∥CN,
∴∠AEH=∠ENC,∠BEC=∠ECN,
∵∠AEH=∠BEC,
∴∠ENC=∠ECN,
∴EN=EC,
∴CN=2CG=2BE,
∵BE=x,DN=y,CD=AB=4,
∴y=2x﹣4(2≤x≤3);
(3)∵∠BAD=90°,
∴∠AFE+∠AEF=90°,
∵EF⊥EC,
∴∠AEF+∠CEB=90°,
∴∠AFE=∠CEB,
∴∠HFE=∠AEC,
当△FHE与△AEC相似时,
(ⅰ)若∠FHE=∠EAC,
∵∠BAD=∠B,∠AEH=∠BEC,
∴∠FHE=∠ECB,
∴∠EAC=∠ECB,
∴,
∵AB=4,BC=3,
∴BE=,
∵设BE=x,DN=y,y=2x﹣4,
∴DN=;
(ⅱ)若∠FHE=∠ECA,如所示,设EG与AC交于点O,
∵EN=EC,EG⊥CN,
∴∠1=∠2,
∵AH∥EG,
∴∠FHE=∠1,
∴∠FHE=∠2,
∴∠2=∠ECA,
∴EO=CO,
设EO=CO=3k,则AE=4k,AO=5k,
∴AO+CO=8k=5,
∴k=,
∴AE=,BE=,
∴DN=1,
综上所述,线段DN的长为或1时△FHE与△AEC相似.
20.证明:(1)作EH⊥CD,EQ⊥AB,
∵AC=BC,CD⊥AB,∠ACB=90°,
∴∠ADC=90°,∠A=∠ACD=45°,
∵EH⊥CD,EQ⊥AB,
∴∠AQE=∠EHC=90°,
在△AEQ与△ECH中,
,
∴△AEQ≌△ECH(AAS),
∴EQ=EH,
∵EH⊥CD,EQ⊥AB,CD⊥AB,
∴四边形EQDH是矩形,
∴∠QEH=90°,
∴∠FEQ=∠GEH=90°﹣∠QEB,
又∵∠EQF=∠EHG=90°,EQ=EH,
∴Rt△EFQ≌Rt△EGH,
∴EF=EG;
(2)过E作EQ⊥AB,EH⊥CD,
∵CD⊥AB,
∴EQ∥CD,EH∥AB,
∵EF⊥BE,
∴∠EFQ+∠EBF=90°,
∵∠EBF+∠DGB=90°,∠DGB=∠EGH(对顶角相等)
∴∠EFQ=∠EGH,
∴△EFQ∽△EGH,
∴=,
在△ADC中,
∵EQ∥CD,
∴=,
又∵CE=kEA,
∴AC=(k+1)AE
∴CD=(k+1)EQ,
同理=,
∴AD=EH,
∵∠ACB=90°,CD⊥AB,AC=mBC
即=,
∴=,
∴EF=EG.
解答专项练习题(附答案)
1.如图,在△ABC中,点D,E分别在边AB,AC上,且BE平分∠ABC,∠ABE=∠ACD,BE,CD交于点G.
(1)求证:=;
(2)连接DE,求证:DE=CE;
(3)若CD⊥AB,AD=2,BD=3,求线段EG的长.
2.如图,在Rt△ABC中,AC=4,∠BAC=90°,∠B=30°,D是BC上一点,AE⊥AD,∠ADE=30°,连接CE.
(1)求证:△ADE∽△ABC;
(2)求证:△ACE∽△ABD;
(3)设CE=x,当CD=2CE时,求x的值.
3.如图,在△ABC中,AG⊥BC,垂足为点G,点E为边AC上一点,BE=CE,点D为边BC上一点,GD=GB,连接AD交BE于点F.
(1)求证:∠ABE=∠EAF;
(2)求证:AE2=EF EC;
(3)若CG=2AG,AD=2AF,BC=5,求AE的长.
4.如图,E是矩形ABCD的边BC上的一点,AC是其对角线,连接AE,过点E作EF⊥AE,EF交AC于点M,EF交DC于点F,过点B作BG⊥AC于点G,BG交AE于点H.
(1)求证:△ABE∽△ECF;
(2)求证:AH CM=BH EM;
(3)若E是BC的中点,=,AB=6,求EM的长.
5.如图,△ABC中,DE∥BC,G是AE上一点,连接BG交DE于F,作GH∥AB交DE于点H.
(1)如图1,与△GHE相似的三角形是 (直接写出答案);
(2)如图1,若AD=3BD,BF=FG,求的值;
(3)如图2,连接CH并延长交AB于P点,交BG于Q,连接PF,则一定有PF∥CE,请说明理由.
6.如图,在Rt△ABC中,∠C=90°,AD平分∠BAC交BC于点D,DE⊥AD交AB于E,EF∥BC交AC于F.
(1)求证:△ACD∽△ADE;
(2)求证:AD2=AB AF;
(3)作DG⊥BC交AB于G,连接FG,若FG=5,BE=8,直接写出AD的长.
7.已知四边形ABCD是矩形,AB=2,BC=4,E为BC边上一动点且不与B、C重合,连接AE(1)如图1,过点E作EN⊥AE交CD于点N.
①若BE=1,求CN的长;
②将△ECN沿EN翻折,点C恰好落在边AD上,求BE的长;
(2)如图2,连接BD,设BE=m,试用含m的代数式表示S四边形CDFE:S△ADF值.
8.如图,正方形ABCD的对角线AC,BD相交于点O,点P是BC延长线上一点,连接AP,分别交BD,CD于点E,F,过点B作BG⊥AP于G,交线段AC于H.
(1)若∠P=25°,求∠AHG的大小;
(2)求证:AE2=EF EP.
9.如图,在正方形ABCD中,边长为4,∠MDN=90°,将∠MDN绕点D旋转,其中DM边分别与射线BA、直线AC交于E、Q两点,DN边与射线BC交于点F;连接EF,且EF与直线AC交于点P.
(1)如图1,点E在线段AB上时,
①求证:AE=CF;
②求证:DP垂直平分EF;
(2)当AE=1时,求PQ的长.
10.如图,∠ABC=∠DBE=90°,C是DE的中点.
(1)求证:△ABD∽△AEB;
(2)当=时,求的值;
(3)在(2)的条件下,作∠BAC的平分线,与BE交于点F,若AF=8,求DE的长.
11.如图,已知:正方形ABCD,点E在CB的延长线上,连接AE、DE,DE与边AB交于点F,FG∥BE交AE于点G.
(1)求证:GF=BF;
(2)若EB=1,BC=4,求AG的长;
(3)在BC边上取点M,使得BM=BE,连接AM交DE于点O.求证:FO ED=OD EF.
12.阅读下面材料:小昊遇到这样一个问题:如图1,在△ABC中,BE是AC边上的中线,点D在BC边上,=,AD与BE相交于点P,求的值.
小昊发现,过点C作CF∥AD,交BE的延长线于点F,通过构造△CEF,经过推理和计算能够使问题得到解决(如图2).
请回答:的值为 .
参考小昊思考问题的方法,解决问题:
(1)如图3,在△ABC中,点D在BC的延长线上,,点E在AC上,且.求的值;
(2)如图4,在△ABC中,点D在BC的延长线上,,点E在AC上,且,直接写出的值为 .
13.如图1所示,点A、D、C、E在同一直线上,满足∠ABC=90°,BD⊥BE,且CD=CB=CE.
(1)求证:△ABD∽△AEB;
(2)若AB=BC,求的值;
(3)如图2所示,在(2)的条件下,∠BAE的平分线交BE于F,AF=2,求BC的值.
14.已知:在△ABC中,点D在BC边上,过点C作一直线与边AB及AD分别交于点F、E.
(1)如图,当=时,求证:=;
(2)如图,当=时,猜想:与之间是否存在着一定的数量关系?若存在,请写出它们之间的关系式,并给出证明过程;若不存在,请说明理由.
15.在Rt△ABC中,∠BAC=90°,过点B的直线MN∥AC,D为BC边上一点,连接AD,作DE⊥AD交MN于点E,连接AE.
(1)如图①,当∠ABC=45°时,求证:AD=DE;
(2)如图②,当∠ABC=30°时,线段AD与DE有何数量关系?并请说明理由;
16.已知Rt△ABC中,∠AOB=90°,,∠OAB=30°,点D在线段AO上,连接BD,如图1,过点D作DE⊥AB 于点E.
(1)F为BD的中点,连接OF、EF,若OD=8,求EF的长.
(2)将图1中的△ADE绕点A旋转,使D、E、B三点在一条直线上,如图2,过点O作OG⊥OE交BD于点G.
①求的值;
②若点F为线段BD的中点,,直接写出线段OF的长度.
17.已知:在正方形ABCD中,E为BC延长线上一点,连接AE分别交DC、DB于F、G.求证:
(1)∠DAG=∠DCG;
(2)AG2=GE GF;
(3)已知,,求该正方形的边长.
18.在锐角△ABC中,AB=4,BC=5,∠ACB=45°,将△ABC绕点B按逆时针方向旋转,得到△A1BC1.
(1)如图1,当点C1在线段CA的延长线上时,求∠CC1A1的度数;
(2)如图2,连接AA1,CC1.若△ABA1的面积为4,求△CBC1的面积;
(3)如图3,点E为线段AB中点,点P是线段AC上的动点,在△ABC绕点B按逆时针方向旋转过程中,点P的对应点是点P1,求线段EP1长度的最大值与最小值.
19.在矩形ABCD中,AB=4,BC=3,E是AB边上一点,EF⊥CE交AD于点F,过点E作∠AEH=∠BEC,交射线FD于点H,交射线CD于点N.
(1)如图a,当点H与点F重合时,求BE的长;
(2)如图b,当点H在线段FD上时,设BE=x,DN=y,求y与x之间的函数关系式,并写出它的定义域;
(3)连接AC,当△FHE与△AEC相似时,求线段DN的长.
20.如图,∠ACB=90°,CD⊥AB,垂足为D,点E在AC上,BE交CD于点G,EF⊥BE交AB于点F.
(1)如图①,若AC=BC,CE=EA,探索线段EF与EG的数量关系,并证明你的结论;
(2)如图②,若AC=mBC,CE=kEA,探索线段EF与EG的数量关系,并证明你的结论.
参考答案
1.证明:(1)∵∠ABE=∠ACD,∠A=∠A,
∴△ABE∽△ACD,
∴;
(2)∵,
∴,
又∵∠A=∠A,
∴△ADE∽△ACB,
∴∠AED=∠ABC,
∵∠AED=∠ACD+∠CDE,∠ABC=∠ABE+∠CBE,
∴∠ACD+∠CDE=∠ABE+∠CBE,
∵∠ABE=∠ACD,
∴∠CDE=∠CBE,
∵BE平分∠ABC,
∴∠ABE=∠CBE,
∴∠CDE=∠ABE=∠ACD,
∴DE=CE;
(3)∵CD⊥AB,
∴∠ADC=∠BDC=90°,
∴∠A+∠ACD=∠CDE+∠ADE=90°,
∵∠ABE=∠ACD,∠CDE=∠ACD,
∴∠A=∠ADE,∠BEC=∠ABE+∠A=∠A+∠ACD=90°,
∴AE=DE,BE⊥AC,
∵DE=CE,
∴AE=DE=CE,
∴AB=BC,
∵AD=2,BD=3,
∴BC=AB=AD+BD=5,
在Rt△BDC中,CD===4,
在Rt△ADC中,AC===2,
∴DE=AE=CE=,
∵∠ADC=∠GEC=90°,∠ACD=∠GCE,
∴△CGE∽△CAD,
∴,
∴GE===.
2.(1)证明:∵AE⊥AD,∠BAC=90°,
∴∠EAD=∠CAB=90°,
∵∠B=30°,∠ADE=30°,
∴∠B=∠ADE,
∴△ADE∽△ABC;
(2)证明:∵∠EAD=∠CAB=90°,
∴∠EAC=∠DAB=90°﹣∠CAD,
∵△ADE∽△ABC,
∴=,
∴=,
∴△ACE∽△ABD;
(3)解:在Rt△ABC中,∠CAB=90°,AC=4,∠B=30°,
∴BC=2AC=8,AB===4,
∵CE=x,CD=2CE,
∴CD=2x,
∵△ACE∽△ABD,
∴=,
∴=,
∴BD=x,
∴BC=CD+BD=2x+x=8,
解得:x=16﹣8.
3.(1)证明:∵EB=EC,
∴∠EBC=∠C,
∵AG⊥BD,BG=GD,
∴AB=AD,
∴∠ABD=∠ADB,
∵∠ABD=∠ABE+∠EBC,∠ADB=∠DAC+∠C,
∴∠ABE=∠DAC,
即∠ABE=∠EAF.
(2)证明:∵∠AEF=∠BEA,∠EAF=∠ABE,
∴△AEF∽△BEA,
∴=,
∴AE2=EF EB,
∵EB=EC,
∴AE2=EF EC.
(3)解:设BE交AG于J,连接DJ,DE.
∵AG垂直平分线段BD,
∴JB=JD,
∴∠JBD=∠JDG,
∵∠JBD=∠C,
∴∠JDB=∠C,
∴DJ∥AC,
∴∠AEF=∠DJF,
∵AF=DF,∠AFE=∠DFJ,
∴△AFE≌△DFJ(AAS),
∴EF=FJ,AE=DJ,
∵AF=DF,
∴四边形AJDE是平行四边形,
∴DE∥AG,
∵AG⊥BC,
∴ED⊥BC,
∵EB=EC,
∴BD=DC=,
∴BG=DG=,
∵tan∠JDG=tan∠C===,
∴JG=,
∵∠JGD=90°,
∴DJ===,
∴AE=DJ=.
4.(1)证明:∵四边形ABCD是矩形,
∴∠ABE=∠ECF=90°.
∵AE⊥EF,∠AEB+∠FEC=90°.
∴∠AEB+∠BAE=90°,
∴∠BAE=∠CEF,
∴△ABE∽△ECF;
(2)证明:∵BG⊥AC,
∴∠ABG+∠BAG=90°,
∴∠ABH=∠ECM,
由(1)知,∠BAH=∠CEM,
∴△ABH∽△ECM;,
∴=,
∴AH CM=BH EM;
(3)解:作MR⊥BC,垂足为R,
∵=,AB=6,
∴BC=8,
∵E是BC的中点,
∴BE=EC=4,
∵△ABE∽△ECF,
∴=,即=
∴CF=,
∵CD∥RM∥AB,
∴△ERM∽△ECF,△CRM∽△CBA,
∴=,=,即=,=,
∴RM=,
∵=,
∴=,
∴=,
∵△ABE∽△ECF,
∴==,
∴==,
∴EM=RM=×=.
5.(1)解:如图1中,
∵GH∥AD,
∴△GHE∽△ADE,
∵DE∥BC,
∴△ADE∽△ABC,
∴△GHE∽△ADE∽△ABC,
故答案为△ADE,△ABC.
(2)解:∵GH∥BD,
∴∠FGH∠DBF,
∵BF=FG,∠DFB=∠GFH,
∴△BFD≌△GFH(ASA),
∴BD=GH,
∵GH∥AD,
∴===,
∴=.
(3)证明:如图2中,
∵GH∥BD,
∴=,
∵GH∥PA,
∴=,
∵DH∥BC,
∴=,
∴=,
∴=,
∴=,
∴PF∥AG,即PF∥AC.
6.(1)证明:∵DA平分∠BAC,
∴∠CAD=∠DAE,
∵DE⊥AD,
∴∠ADE=∠C=90°,
∴△ACD∽△ADE.
(2)证明:连接DF.
∵EF∥BC,
∴∠AFE=∠C=90°,∠AEF=∠B,
∵∠ADE=∠AFE=90°,
∴A,E,D,F四点共圆,
∴∠ADF=∠AEF,
∴∠B=∠ADF,
∴∠DAB=∠DAF,
∴△BAD∽△DAF,
∴=,
∴AD2=AB AF.
(3)解:设DG交EF于O.
∵DG⊥BC,AC⊥BC,
∴DG∥AC,
∴∠ADG=∠DAC=∠DAG,
∴AG=GD,
∵∠AED+∠EAD=90°,∠EDG+∠ADG=90°,
∴∠GED=∠GDE,
∴DG=EG=AG,
∵∠AFE=90°,
∴FG=EG=AG=DG=5,
∵OE∥BD,
∴=,
∴=,
∴OG=,
∴OG∥AF.EG=AG,
∴OE=OF,
∴AF=2OG=,
∴AD2=AB AF=18×,
∵AD>0,
∴AD=.
7.解:(1)①∵BE=1,
∴CE=BC﹣BE=4﹣1=3,
∵四边形ABCD是矩形,
∴∠B=∠C=90°,
∴∠BAE+∠BEA=90°,
∵EF⊥AE,
∴∠AEF=90°,
∴∠BEA+∠FEC=90°,
∴∠BAE=∠FEC,
∴△ABE∽△ECN,
∴=,
即:=,
解得:CN=;
②过点E作EF⊥AD于F,如图1所示:
则四边形ABEF是矩形,
∴AB=EF=2,AF=BE,
由折叠的性质得:CE=C′E,CN=C′N,∠EC′N=∠C=90°,
∴∠NC′D+∠EC′F=90°,
∵∠C′ND+∠NC′D=90°,
∴∠EC′F=∠C′ND,
∵∠D=∠EFC′,
∴△EC′F∽△NC′D,
∴==,
∴==,
∵=,
∴=,
∴==,
∴C′D=BE,
设BE=x,则C′D=AF=x,C′F=4﹣2x,CE=4﹣x,
∴=,=,
∴DN=x(2﹣x),CN=,
∴CN+DN=x(2﹣x)+=CD=2,
解得:x=2或x=,
∴BE=2或BE=;
(2)∵四边形ABCD为矩形,
∴BC=AD,AD∥BC,
∴△ADF∽△EBF,
∴==,
∴=()2=,
∴S△ADF=s△BEF,
S△ABF===S△BEF,
S四边形CDFE=S△ADF+S△ABF﹣S△BEF=S△BEF+S△BEF﹣S△BEF=(+﹣1)S△BEF,
∴S四边形CDFE:S△ADF=(+﹣1)S△BEF:s△BEF=1+﹣.
8.(1)解:∵四边形ABCD是正方形,
∴∠ACB=45°,
∵∠ACB=∠P+∠CAP,
∴∠CAP=20°,
∵BG⊥AP,
∴∠AGH=90°,
∴AHG=90°﹣20°=70°.
(2)证明:∵四边形ABCD是正方形,
∴A,C关于BD对称,∠ACB=∠ACD=45°,
∴EA=EC,
∴∠EAC=∠ECA,
∵∠ACB=∠P+∠CAE=45°,∠ECF+∠ECA=45°,
∴∠ECF=∠P,
∵∠CEF=∠PEC,
∴△CEF∽△PEC,
∴=,
∴EC2=EF EP,
∴EA2=EF EP.
9.(1)①证明:∵四边形ABCD是正方形,
∴DA=DC,∠ADC=∠DAE=∠DCF=90°,
∴∠ADC=∠MDN=90°,
∴∠ADE=∠CDF,
∴△ADE≌△CDF(ASA),
∴AE=CF.
②∵△ADE≌△CDF(ASA),
∴DE=DF,∵∠MDN=90°,
∴∠DEF=45°,
∵∠DAC=45°,
∴∠DAQ=∠PEQ,∵∠AQD=∠EQP,
∴△AQD∽△EQP,
∴=,
∴=,∵∠AQE=∠PQD,
∴△AQE∽△DQP,
∴∠QDP=∠QAE=45°,
∴∠DPE=90°,
∴DP⊥EF,∵DE=DF,
∴PE=PF,
∴DP垂直平分线段EF.
(2)解:①当点E在线段AB上时,作QH⊥AD于H,QG⊥AB于G.
在Rt△ADE中,DE==,
∵∠QAH=∠QAG=45°,
∴HQ=QG=AH=AG,设QH=x,
∵×4×x+×1×x=×1×4,
∵x=,
∴AQ=,DQ==,EQ=,
∵△AQD∽△EQP,
∴AQ PQ=DQ EQ,
∴PQ==.
②当点E在BA的延长线上时,作QH⊥AD于H,QG⊥AB于G.
在Rt△ADE中,DE==,
∵∠QAH=∠QAG=45°,
∴HQ=QG=AH=AG,设QH=x,
∵×4×x﹣×1×x=×1×4,
∵x=,
∴AQ=,DQ==,EQ=,
∵△AQD∽△EQP,
∴AQ PQ=DQ EQ,
∴PQ==.
综上所述,PQ的长为或.
10.解:(1)证明:∵∠ABC=∠DBE=90°,
∴∠ABD+∠CBD=90°,
∵∠DBE=90°,C是DE的中点.
∴BC=CD=CE,
∴∠E=∠CBE.
∵∠CBE+∠CBD=90°,∠ABD+∠CBD=90°,
∴∠CBE=∠ABD,
∴∠E=∠ABD,
又∵∠BAD=∠EAB,
∴△ABD∽△AEB;
(2)∵=,
∴设AB=4,BC=3,
∴AC==5,
∵BC=CD=3,
∴AD=AC﹣CD=5﹣3=2,
由(1)可知:△ABD∽△AEB,
∴==,
∴AB2=AD AE,
∴42=2AE,
∴AE=8,
∴===;
∴的值为;
(3)过点F作FG⊥AE于点G,
∵=,
∴设AB=4x,BC=3x,
由(2)可知:AE=8x,AD=2x,
∴DE=AE﹣AD=6x,
∵AF平分∠BAC,
∴=,
∴==,
∵tanE==,
∴cosE=,sinE=,
∴=,
∴BE=x,
∴EF=BE=x,
∴sinE==,
∴FG=x,
∵tanE=,
∴GE=2GF=x,
∴AG=AE﹣GE=x,
∵AF2=AG2+GF2,AF=8,
∴64=+,
∴x=,
∴DE=6x=3.
∴DE的长为3.
11.证明:(1)∵四边形ABCD是正方形,
∴AD∥BC,AB∥CD,AD=CD,
∵GF∥BE,
∴GF∥BC,
∴GF∥AD,
∴,
∵AB∥CD,
,
∵AD=CD,
∴GF=BF;
(2)∵EB=1,BC=4,
∴=4,AE=,
∴==4,
∴AG=;
(3)延长GF交AM于H,∵GF∥BC,
∴FH∥BC
∴=,
∴=,
∵BM=BE,
∴GF=FH,
∵GF∥AD,
∴,,
∴,
∴=,
∴FO ED=OD EF.
12.解:如图2,过点C作CF∥AD,交BE的延长线于点F,
∴∠F=∠APF,∠FCE=∠EAP,
∵BE为AC边的中线,
∴AE=CE,
∴△AEP≌△CEF(AAS),
∴AP=FC,
∵PD∥FC,
∴△BPD∽△BFC,
∴=,
∴=,
故答案为:;
(1)如图3,过A作AF∥BC,交BP延长线于点F,
∴△AFE∽△CBE,
∴,
∵,
∴,
设AF=3x,BC=2x,
∵,
∴BD=3x,
∴AF=BD=3x,
∵AF∥BD,
∴△AFP∽△DBP,
∴==1;
(2)如图4,过C作CF∥AP交PB于F,
∴△BCF∽△BDP,
∴,
设CF=2x,PD=3x,
∵CF∥AP,
∴△ECF∽△EAP,
∴,
∴AP=7x,AD=4x,
∴.
故答案为:.
13.解:(1)∵∠ABC=90°,∠DBE=90°,
∴∠ABD=∠CBE,
∵BC=CE,
∴∠CBE=∠E,
∴∠ABD=∠E,
∵∠A=∠A,
∴△ABD∽△AEB;
(2)∵AB:BC=4:3,
∴设AB=4,BC=3,
∴AC==5,
∵BC=CD=3,
∴AD=AC﹣CD=5﹣3=2,
由(1)可知:△ABD∽△AEB,
∴==,
∴AB2=AD AE,
∴42=2AE,
∴AE=8,
在Rt△DBE中
===;
(3)过点F作FM⊥AE于点M,
∵AB:BC=4:3,
∴设AB=4x,BC=3x,
∴由(2)可知;AE=8x,AD=2x,
∴DE=AE﹣AD=6x,
作FN⊥AB,交AB延长线于点N,作AP⊥EB,交EB于点P,
∴S△ABF=AB FN=BF AP,S△AEF=EF AP=AE FM,
∵AF平分∠BAC,
∴FN=FM,
∴==,
∴==,
∴=,
∴BE=x,
∴EF=BE=x,
∴MF=x,
∴ME=2MF=x,
∴AM=AE﹣ME=x,
∵AF2=AM2+MF2,
∴4=(x)2+(x)2,
∴x=,
BC=3x=.
14.解:(1)如图1,过D作DG∥FC交AB于G,
∴=,
∴FB,
∵EF∥DG
∴;
(2)猜想,
证明:如图2,过D作DG∥FC交AB于G,
∴,
∴FG=,
∴=.
15.(1)证明:如图1,过点D作DF⊥BC,交AB于点F,
则∠BDE+∠FDE=90°,
∵DE⊥AD,
∴∠FDE+∠ADF=90°,
∴∠BDE=∠ADF,
∵∠BAC=90°,∠ABC=45°,
∴∠C=45°,
∵MN∥AC,
∴∠EBD=180°﹣∠C=135°,
∵∠BFD=45°,DF⊥BC,
∴∠BFD=45°,BD=DF,
∴∠AFD=135°,
∴∠EBD=∠AFD,
在△BDE和△FDA中
,
∴△BDE≌△FDA(ASA),
∴AD=DE;
(2)解:DE=AD,
理由:如图2,过点D作DG⊥BC,交AB于点G,
则∠BDE+∠GDE=90°,
∵DE⊥AD,
∴∠GDE+∠ADG=90°,
∴∠BDE=∠ADG,
∵∠BAC=90°,∠ABC=30°,
∴∠C=60°,
∵MN∥AC,
∴∠EBD=180°﹣∠C=120°,
∵∠ABC=30°,DG⊥BC,
∴∠BGD=60°,
∴∠AGD=120°,
∴∠EBD=∠AGD,
∴△BDE∽△GDA,
∴=,
在Rt△BDG中,
=,
∴DE=AD;
16.解:(1)在Rt△ABC中,∠AOB=90°,,∠OAB=30°,
∴OB=6,AB=12,
在Rt△OBD中,∵OD=8,
∴BD==10,
∵DE⊥AB,
∴∠DEB=90°,
∴EF=BD=5;
(2)①∵∠AOB=90°,
∵OG⊥OE,
∴∠EOG=90°,
∴∠AOB﹣∠AOG=∠EOG﹣∠AOG,
∴∠AOE=∠BOG,
∵∠AEG+∠OEG=∠EOG+∠OEG,
∴∠AEO=∠OGB,
∴△AEO∽△OGB,
∴==;
②在Rt△ADE中,∵∠DAE=30°,AD=2,
∴AE=3,DE=,
∵=;
∴BG=,
∴DE=BG,
∵点F为线段BD的中点,
∴点F为线段EG的中点,
在Rt△AEB中,
BE==3,
∴EG=3﹣,
∴OF=EG=.
17.(1)证明:∵四边形ABCD是正方形,
∴AD=BC,∠ADG=∠CDG=45°,
在△ADG和△CDG中,
,
∴△ADG≌△CDG(SAS),
∴∠DAG=∠DCG;
(2)∵AD∥BE,
∴∠DAG=∠E,
∵△ADG≌△CDG,
∴∠DAG=∠GCD,AG=CG,
∴∠GCD=∠E,
∵∠GCE=∠GCD+90°,∠GFC=∠DAG+90°,
∴∠GFC=∠GCE,
∴△GCF∽△GEC,
∴CG2=GE GF,
∴AG2=GE GF;
(3)∵,,
∴GE=GF+EF=3﹣3,
∵CG2=GE GF,
∴CG=3﹣,
∴GF:CG=CF:CE=1:,
∵EF=2﹣2,
∴CF=﹣1,CE=3﹣3,
∵CF∥AB,
∴△EFC∽△EAB,
∴,
∴,
解得:AB=.
18.解:(1)由旋转的性质可得:∠A1C1B=∠ACB=45°,BC=BC1,
∴∠CC1B=∠C1CB=45°,
∴∠CC1A1=∠CC1B+∠A1C1B=45°+45°=90°.
(2)∵△ABC≌△A1BC1,
∴BA=BA1,BC=BC1,∠ABC=∠A1BC1,
∴,∠ABC+∠ABC1=∠A1BC1+∠ABC1,
∴∠ABA1=∠CBC1,
∴△ABA1∽△CBC1.
∴,
∵S△ABA1=4,
∴S△CBC1=;
(3)①如图1,过点B作BD⊥AC,D为垂足,
∵△ABC为锐角三角形,
∴点D在线段AC上,
在Rt△BCD中,BD=BC×sin45°=,
当P在AC上运动,BP与AC垂直的时候,△ABC绕点B旋转,使点P的对应点P1在线段AB上时,EP1最小,最小值为:EP1=BP1﹣BE=BD﹣BE=﹣2;
②当P在AC上运动至点C,△ABC绕点B旋转,使点P的对应点P1在线段AB的延长线上时,EP1最大,最大值为:EP1=BC+BE=2+5=7.
19.解:(1)∵EF⊥EC,
∴∠AEF+∠BEC=90°,
∵∠AEF=∠BEC,
∴∠AEF=∠BEC=45°,
∵∠B=90°,
∴BE=BC,
∵BC=3,
∴BE=3;
(2)过点E作EG⊥CN,垂足为点G,
∴四边形BEGC是矩形,
∴BE=CG,
∵AB∥CN,
∴∠AEH=∠ENC,∠BEC=∠ECN,
∵∠AEH=∠BEC,
∴∠ENC=∠ECN,
∴EN=EC,
∴CN=2CG=2BE,
∵BE=x,DN=y,CD=AB=4,
∴y=2x﹣4(2≤x≤3);
(3)∵∠BAD=90°,
∴∠AFE+∠AEF=90°,
∵EF⊥EC,
∴∠AEF+∠CEB=90°,
∴∠AFE=∠CEB,
∴∠HFE=∠AEC,
当△FHE与△AEC相似时,
(ⅰ)若∠FHE=∠EAC,
∵∠BAD=∠B,∠AEH=∠BEC,
∴∠FHE=∠ECB,
∴∠EAC=∠ECB,
∴,
∵AB=4,BC=3,
∴BE=,
∵设BE=x,DN=y,y=2x﹣4,
∴DN=;
(ⅱ)若∠FHE=∠ECA,如所示,设EG与AC交于点O,
∵EN=EC,EG⊥CN,
∴∠1=∠2,
∵AH∥EG,
∴∠FHE=∠1,
∴∠FHE=∠2,
∴∠2=∠ECA,
∴EO=CO,
设EO=CO=3k,则AE=4k,AO=5k,
∴AO+CO=8k=5,
∴k=,
∴AE=,BE=,
∴DN=1,
综上所述,线段DN的长为或1时△FHE与△AEC相似.
20.证明:(1)作EH⊥CD,EQ⊥AB,
∵AC=BC,CD⊥AB,∠ACB=90°,
∴∠ADC=90°,∠A=∠ACD=45°,
∵EH⊥CD,EQ⊥AB,
∴∠AQE=∠EHC=90°,
在△AEQ与△ECH中,
,
∴△AEQ≌△ECH(AAS),
∴EQ=EH,
∵EH⊥CD,EQ⊥AB,CD⊥AB,
∴四边形EQDH是矩形,
∴∠QEH=90°,
∴∠FEQ=∠GEH=90°﹣∠QEB,
又∵∠EQF=∠EHG=90°,EQ=EH,
∴Rt△EFQ≌Rt△EGH,
∴EF=EG;
(2)过E作EQ⊥AB,EH⊥CD,
∵CD⊥AB,
∴EQ∥CD,EH∥AB,
∵EF⊥BE,
∴∠EFQ+∠EBF=90°,
∵∠EBF+∠DGB=90°,∠DGB=∠EGH(对顶角相等)
∴∠EFQ=∠EGH,
∴△EFQ∽△EGH,
∴=,
在△ADC中,
∵EQ∥CD,
∴=,
又∵CE=kEA,
∴AC=(k+1)AE
∴CD=(k+1)EQ,
同理=,
∴AD=EH,
∵∠ACB=90°,CD⊥AB,AC=mBC
即=,
∴=,
∴EF=EG.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
