2022--2023学年人教版八年级数学上册12.2.4全等三角形的判断 HL 一课一练 (word、含答案)
文档属性
| 名称 | 2022--2023学年人教版八年级数学上册12.2.4全等三角形的判断 HL 一课一练 (word、含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 119.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-21 00:00:00 | ||
图片预览

文档简介
人教版 八年级数学上册
12.2.4全等三角形的判断 HL
一.选择题
1.使两个直角三角形全等的条件是( )
A.一个锐角对应相等 B.两个锐角对应相等
C.一条边对应相等 D.斜边及一条直角边对应相等
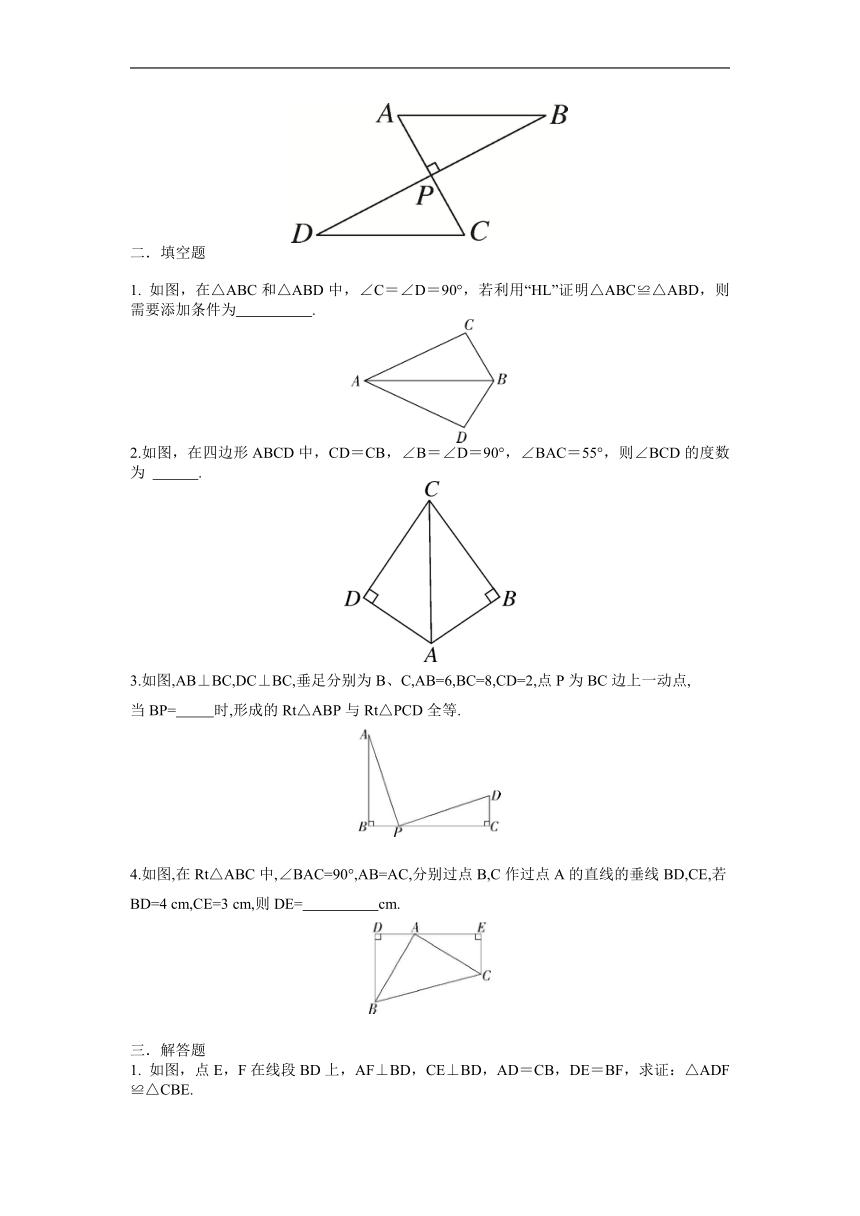
2.如图所示,∠C=∠D=90°,添加一个条件,可使用“HL”判定Rt△ABC与Rt△ABD全等.以下给出的条件适合的是( )
A.AC=AD B.AB=AB
C.∠ABC=∠ABD D.∠BAC=∠BAD
3.如图,已知AC⊥BD,垂足为O,AO=CO,AB=CD,则可得到△AOB≌△COD,理由是( )
A.HL B.SAS C.ASA D.AAS
4.如图,BE=CF,AE⊥BC,DF⊥BC,垂足分别为点E,F,要根据“HL”证明Rt△ABE≌Rt△DCF,则还需要添加的一个条件是( )
A.AE=DF B.∠A=∠D
C.∠B=∠C D.AB=DC
5.如图,AC⊥BD于P,AP=CP,增加下列一个条件:①BP=DP;②AB=CD;③∠A=∠C.其中能判定△ABP≌△CDP的条件有( )
A.0个 B.1个 C.2个 D.3个
二.填空题
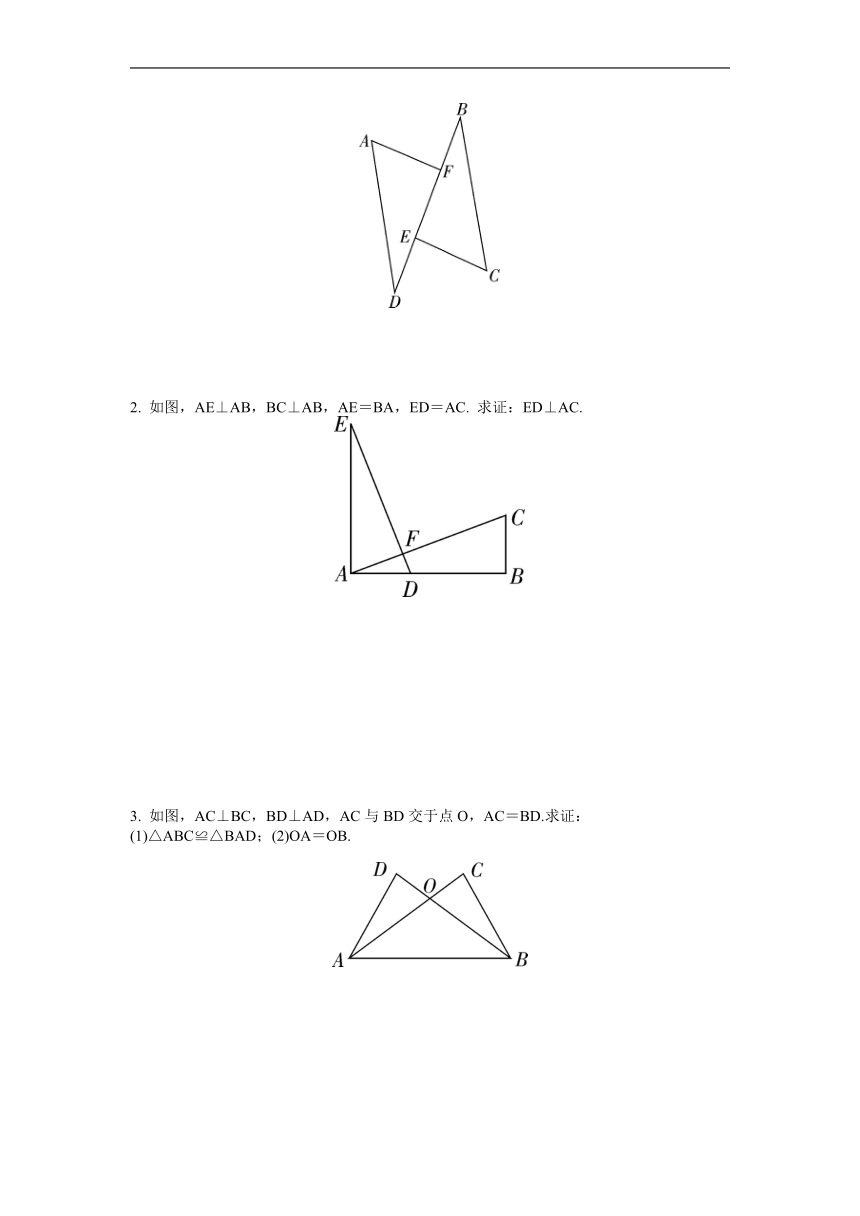
1. 如图,在△ABC和△ABD中,∠C=∠D=90°,若利用“HL”证明△ABC≌△ABD,则需要添加条件为 .
2.如图,在四边形ABCD中,CD=CB,∠B=∠D=90°,∠BAC=55°,则∠BCD的度数为 .
3.如图,AB⊥BC,DC⊥BC,垂足分别为B、C,AB=6,BC=8,CD=2,点P为BC边上一动点,
当BP= 时,形成的Rt△ABP与Rt△PCD全等.
4.如图,在Rt△ABC中,∠BAC=90°,AB=AC,分别过点B,C作过点A的直线的垂线BD,CE,若BD=4 cm,CE=3 cm,则DE= cm.
三.解答题
1. 如图,点E,F在线段BD上,AF⊥BD,CE⊥BD,AD=CB,DE=BF,求证:△ADF≌△CBE.
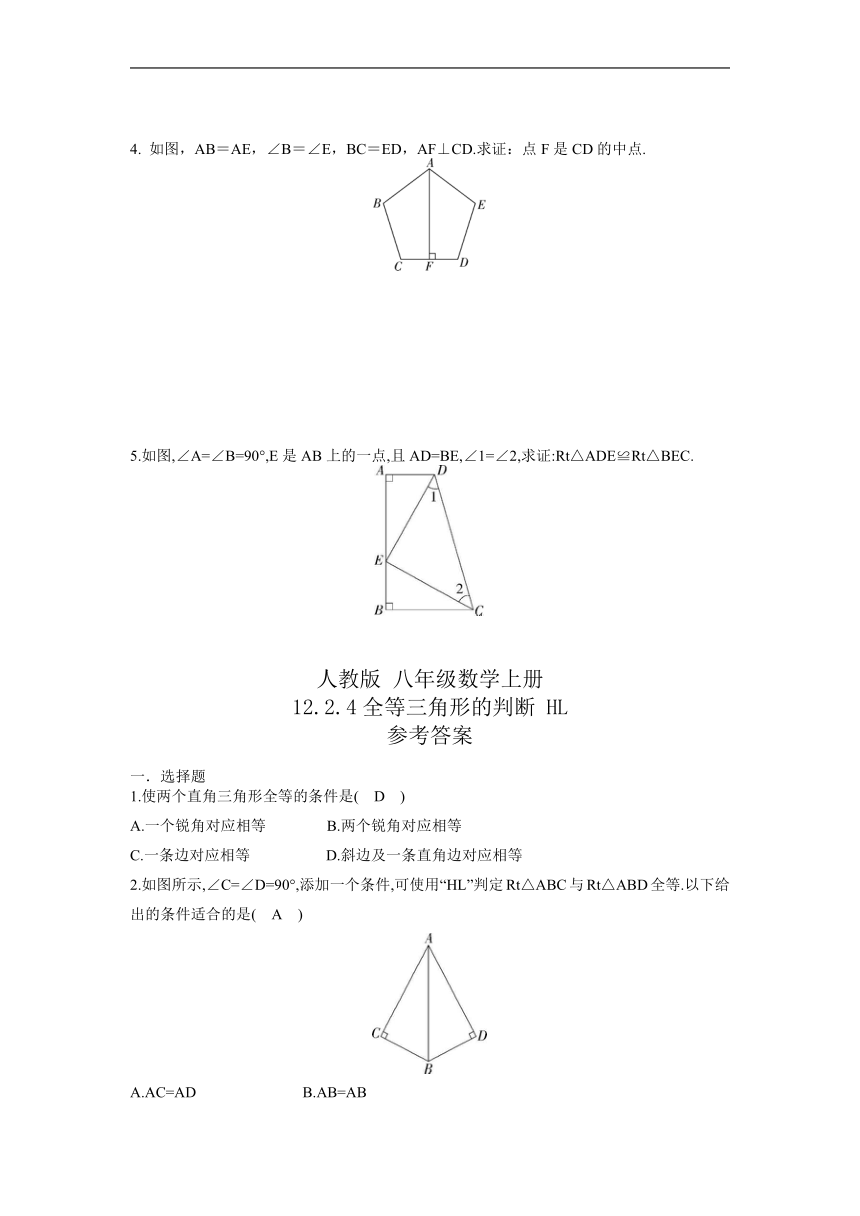
2. 如图,AE⊥AB,BC⊥AB,AE=BA,ED=AC. 求证:ED⊥AC.
3. 如图,AC⊥BC,BD⊥AD,AC与BD交于点O,AC=BD.求证:
(1)△ABC≌△BAD;(2)OA=OB.
4. 如图,AB=AE,∠B=∠E,BC=ED,AF⊥CD.求证:点F是CD的中点.
5.如图,∠A=∠B=90°,E是AB上的一点,且AD=BE,∠1=∠2,求证:Rt△ADE≌Rt△BEC.
人教版 八年级数学上册
12.2.4全等三角形的判断 HL
参考答案
一.选择题
1.使两个直角三角形全等的条件是( D )
A.一个锐角对应相等 B.两个锐角对应相等
C.一条边对应相等 D.斜边及一条直角边对应相等
2.如图所示,∠C=∠D=90°,添加一个条件,可使用“HL”判定Rt△ABC与Rt△ABD全等.以下给出的条件适合的是( A )
A.AC=AD B.AB=AB
C.∠ABC=∠ABD D.∠BAC=∠BAD
3.如图,已知AC⊥BD,垂足为O,AO=CO,AB=CD,则可得到△AOB≌△COD,理由是( A )
A.HL B.SAS C.ASA D.AAS
4.如图,BE=CF,AE⊥BC,DF⊥BC,垂足分别为点E,F,要根据“HL”证明Rt△ABE≌Rt△DCF,则还需要添加的一个条件是( D )
A.AE=DF B.∠A=∠D
C.∠B=∠C D.AB=DC
5.如图,AC⊥BD于P,AP=CP,增加下列一个条件:①BP=DP;②AB=CD;③∠A=∠C.其中能判定△ABP≌△CDP的条件有( D )
A.0个 B.1个 C.2个 D.3个
二.填空题
1. 如图,在△ABC和△ABD中,∠C=∠D=90°,若利用“HL”证明△ABC≌△ABD,则需要添加条件为 BC=BD或AC=AD .
2.如图,在四边形ABCD中,CD=CB,∠B=∠D=90°,∠BAC=55°,则∠BCD的度数为 70°.
3.如图,AB⊥BC,DC⊥BC,垂足分别为B、C,AB=6,BC=8,CD=2,点P为BC边上一动点,
当BP=2 时,形成的Rt△ABP与Rt△PCD全等.
4.如图,在Rt△ABC中,∠BAC=90°,AB=AC,分别过点B,C作过点A的直线的垂线BD,CE,若BD=4 cm,CE=3 cm,则DE= 7 cm.
三.解答题
1. 如图,点E,F在线段BD上,AF⊥BD,CE⊥BD,AD=CB,DE=BF,求证:△ADF≌△CBE.
证明:∵DE=BF,∴DE+EF=BF+EF.
∴DF=BE.在Rt△ADF和Rt△CBE中,
∴Rt△ADF≌Rt△CBE(HL).
2. 如图,AE⊥AB,BC⊥AB,AE=BA,ED=AC. 求证:ED⊥AC.
证明:∵AE⊥AB,BC⊥AB,
AE=BA,ED=AC,
∴Rt△AED≌Rt△BAC(HL).
∴∠E=∠CAB.
∵∠E+∠EDA=90°,
∴∠CAB+∠EDA=90°.
∴∠DFA=90°. ∴ED⊥AC.
3. 如图,AC⊥BC,BD⊥AD,AC与BD交于点O,AC=BD.求证:
(1)△ABC≌△BAD;(2)OA=OB.
证明:(1)∵AC⊥BC,
BD⊥AD,
∴∠ACB=∠ADB=90°.
在Rt△ABC和Rt△BAD中,
∴Rt△ABC≌Rt△BAD(HL).
(2)∵Rt△ABC≌Rt△BAD,
∴∠D=∠C,AD=BC.
在△AOD与△BOC中,
∴△AOD≌△BOC(AAS).
∴OA=OB.
4. 如图,AB=AE,∠B=∠E,BC=ED,AF⊥CD.求证:点F是CD的中点.
证明:连接AC,AD,
在△ABC和△AED中,
∴△ABC≌△AED(SAS).
∴AC=AD.
∵AF⊥CD,
∴∠AFC=∠AFD=90°.
在Rt△AFC与Rt△AFD中,
∴Rt△AFC≌Rt△AFD(HL).∴CF=DF.
∴点F是CD的中点.
5.如图,∠A=∠B=90°,E是AB上的一点,且AD=BE,∠1=∠2,求证:Rt△ADE≌Rt△BEC.
证明 过点E作EF⊥CD于点F(图略),
∴∠EFD=∠EFC=90°,
∵∠1=∠2,EF=EF,
∴△EFD≌△EFC(AAS),∴DE=CE.
∵∠A=∠B=90°,
∴△ADE和△EBC都是直角三角形,
又∵AD=BE,
∴Rt△ADE≌Rt△BEC(HL).
12.2.4全等三角形的判断 HL
一.选择题
1.使两个直角三角形全等的条件是( )
A.一个锐角对应相等 B.两个锐角对应相等
C.一条边对应相等 D.斜边及一条直角边对应相等
2.如图所示,∠C=∠D=90°,添加一个条件,可使用“HL”判定Rt△ABC与Rt△ABD全等.以下给出的条件适合的是( )
A.AC=AD B.AB=AB
C.∠ABC=∠ABD D.∠BAC=∠BAD
3.如图,已知AC⊥BD,垂足为O,AO=CO,AB=CD,则可得到△AOB≌△COD,理由是( )
A.HL B.SAS C.ASA D.AAS
4.如图,BE=CF,AE⊥BC,DF⊥BC,垂足分别为点E,F,要根据“HL”证明Rt△ABE≌Rt△DCF,则还需要添加的一个条件是( )
A.AE=DF B.∠A=∠D
C.∠B=∠C D.AB=DC
5.如图,AC⊥BD于P,AP=CP,增加下列一个条件:①BP=DP;②AB=CD;③∠A=∠C.其中能判定△ABP≌△CDP的条件有( )
A.0个 B.1个 C.2个 D.3个
二.填空题
1. 如图,在△ABC和△ABD中,∠C=∠D=90°,若利用“HL”证明△ABC≌△ABD,则需要添加条件为 .
2.如图,在四边形ABCD中,CD=CB,∠B=∠D=90°,∠BAC=55°,则∠BCD的度数为 .
3.如图,AB⊥BC,DC⊥BC,垂足分别为B、C,AB=6,BC=8,CD=2,点P为BC边上一动点,
当BP= 时,形成的Rt△ABP与Rt△PCD全等.
4.如图,在Rt△ABC中,∠BAC=90°,AB=AC,分别过点B,C作过点A的直线的垂线BD,CE,若BD=4 cm,CE=3 cm,则DE= cm.
三.解答题
1. 如图,点E,F在线段BD上,AF⊥BD,CE⊥BD,AD=CB,DE=BF,求证:△ADF≌△CBE.
2. 如图,AE⊥AB,BC⊥AB,AE=BA,ED=AC. 求证:ED⊥AC.
3. 如图,AC⊥BC,BD⊥AD,AC与BD交于点O,AC=BD.求证:
(1)△ABC≌△BAD;(2)OA=OB.
4. 如图,AB=AE,∠B=∠E,BC=ED,AF⊥CD.求证:点F是CD的中点.
5.如图,∠A=∠B=90°,E是AB上的一点,且AD=BE,∠1=∠2,求证:Rt△ADE≌Rt△BEC.
人教版 八年级数学上册
12.2.4全等三角形的判断 HL
参考答案
一.选择题
1.使两个直角三角形全等的条件是( D )
A.一个锐角对应相等 B.两个锐角对应相等
C.一条边对应相等 D.斜边及一条直角边对应相等
2.如图所示,∠C=∠D=90°,添加一个条件,可使用“HL”判定Rt△ABC与Rt△ABD全等.以下给出的条件适合的是( A )
A.AC=AD B.AB=AB
C.∠ABC=∠ABD D.∠BAC=∠BAD
3.如图,已知AC⊥BD,垂足为O,AO=CO,AB=CD,则可得到△AOB≌△COD,理由是( A )
A.HL B.SAS C.ASA D.AAS
4.如图,BE=CF,AE⊥BC,DF⊥BC,垂足分别为点E,F,要根据“HL”证明Rt△ABE≌Rt△DCF,则还需要添加的一个条件是( D )
A.AE=DF B.∠A=∠D
C.∠B=∠C D.AB=DC
5.如图,AC⊥BD于P,AP=CP,增加下列一个条件:①BP=DP;②AB=CD;③∠A=∠C.其中能判定△ABP≌△CDP的条件有( D )
A.0个 B.1个 C.2个 D.3个
二.填空题
1. 如图,在△ABC和△ABD中,∠C=∠D=90°,若利用“HL”证明△ABC≌△ABD,则需要添加条件为 BC=BD或AC=AD .
2.如图,在四边形ABCD中,CD=CB,∠B=∠D=90°,∠BAC=55°,则∠BCD的度数为 70°.
3.如图,AB⊥BC,DC⊥BC,垂足分别为B、C,AB=6,BC=8,CD=2,点P为BC边上一动点,
当BP=2 时,形成的Rt△ABP与Rt△PCD全等.
4.如图,在Rt△ABC中,∠BAC=90°,AB=AC,分别过点B,C作过点A的直线的垂线BD,CE,若BD=4 cm,CE=3 cm,则DE= 7 cm.
三.解答题
1. 如图,点E,F在线段BD上,AF⊥BD,CE⊥BD,AD=CB,DE=BF,求证:△ADF≌△CBE.
证明:∵DE=BF,∴DE+EF=BF+EF.
∴DF=BE.在Rt△ADF和Rt△CBE中,
∴Rt△ADF≌Rt△CBE(HL).
2. 如图,AE⊥AB,BC⊥AB,AE=BA,ED=AC. 求证:ED⊥AC.
证明:∵AE⊥AB,BC⊥AB,
AE=BA,ED=AC,
∴Rt△AED≌Rt△BAC(HL).
∴∠E=∠CAB.
∵∠E+∠EDA=90°,
∴∠CAB+∠EDA=90°.
∴∠DFA=90°. ∴ED⊥AC.
3. 如图,AC⊥BC,BD⊥AD,AC与BD交于点O,AC=BD.求证:
(1)△ABC≌△BAD;(2)OA=OB.
证明:(1)∵AC⊥BC,
BD⊥AD,
∴∠ACB=∠ADB=90°.
在Rt△ABC和Rt△BAD中,
∴Rt△ABC≌Rt△BAD(HL).
(2)∵Rt△ABC≌Rt△BAD,
∴∠D=∠C,AD=BC.
在△AOD与△BOC中,
∴△AOD≌△BOC(AAS).
∴OA=OB.
4. 如图,AB=AE,∠B=∠E,BC=ED,AF⊥CD.求证:点F是CD的中点.
证明:连接AC,AD,
在△ABC和△AED中,
∴△ABC≌△AED(SAS).
∴AC=AD.
∵AF⊥CD,
∴∠AFC=∠AFD=90°.
在Rt△AFC与Rt△AFD中,
∴Rt△AFC≌Rt△AFD(HL).∴CF=DF.
∴点F是CD的中点.
5.如图,∠A=∠B=90°,E是AB上的一点,且AD=BE,∠1=∠2,求证:Rt△ADE≌Rt△BEC.
证明 过点E作EF⊥CD于点F(图略),
∴∠EFD=∠EFC=90°,
∵∠1=∠2,EF=EF,
∴△EFD≌△EFC(AAS),∴DE=CE.
∵∠A=∠B=90°,
∴△ADE和△EBC都是直角三角形,
又∵AD=BE,
∴Rt△ADE≌Rt△BEC(HL).
