2022--2023学年人教版八年级数学上册12.2.3全等三角形的判断 AAS、ASA 一课一练 (word、含答案)
文档属性
| 名称 | 2022--2023学年人教版八年级数学上册12.2.3全等三角形的判断 AAS、ASA 一课一练 (word、含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 181.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-21 18:30:25 | ||
图片预览

文档简介
人教版 八年级数学上册
12.2.3全等三角形的判断 AAS、ASA
一.选择题
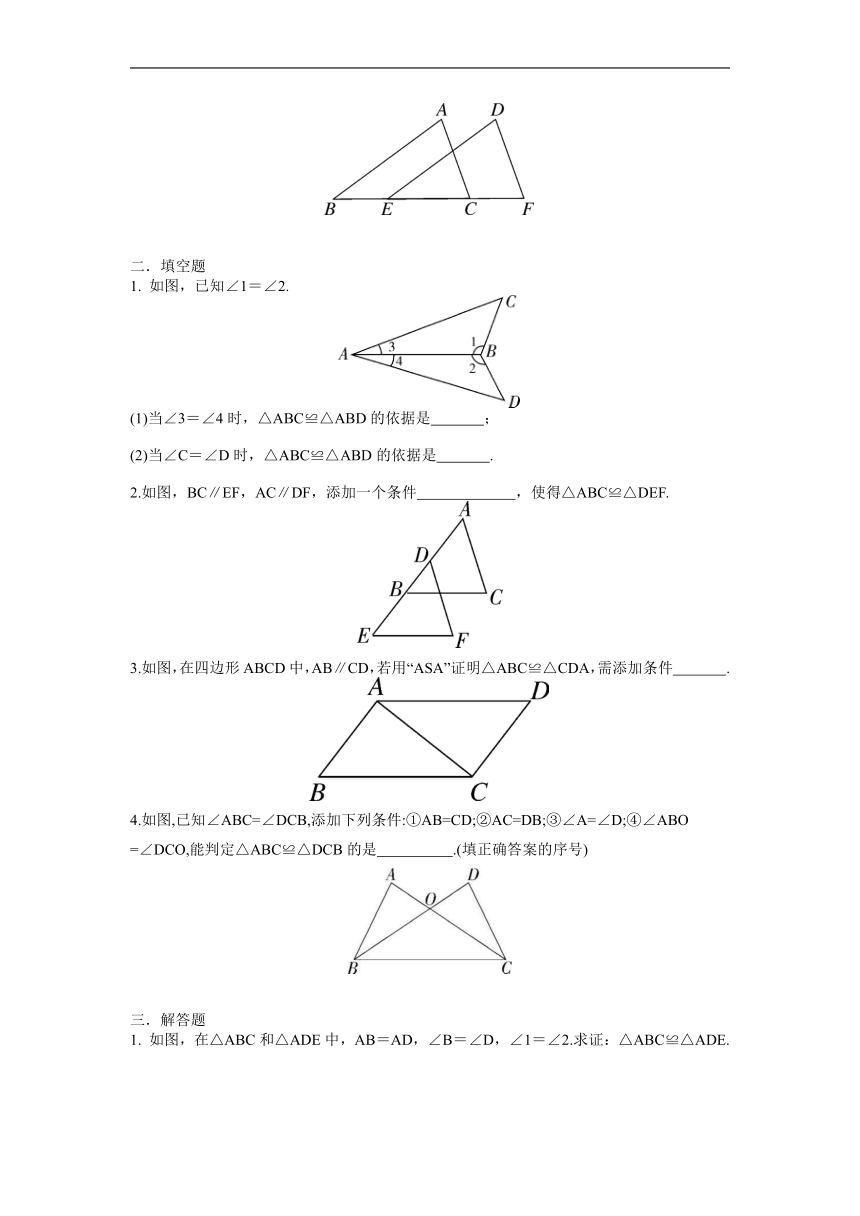
1.已知△ABC的六个元素,下面甲、乙、丙三个三角形中标出了某些元素,则与△ABC全等的三角形是( )
A.只有乙 B.只有丙 C.甲和乙 D.乙和丙
2.如图,∠1=∠2,∠3=∠4,则判定△ABD和△ACD全等的依据是( )
A.SSS B.ASA C.SAS D.AAS
3.如图,在△ABC和△DEF中,已知∠BCA=∠EFD,∠B=∠E,要判定这两个三角形全等,还需要条件( )
A.∠A=∠D B.AB=FD
C.AC=ED D.BC=EF
4.如图,AD∥BC,AB∥DC,AC与BD相交于点O,EF经过点O,且与边AD、BC分别交于E、F两点,若BF=DE,则图中的全等三角形有( )
A.2对 B.3对 C.4对 D.6对
5.如图,已知点B,E,C,F在一条直线上,AC=DF,∠ACB=∠DFE,要使△ABC≌△DEF,不可以添加的条件是( )
A.BE=CF B.∠A=∠D
C.∠B=∠DEF D.AB=DE
二.填空题
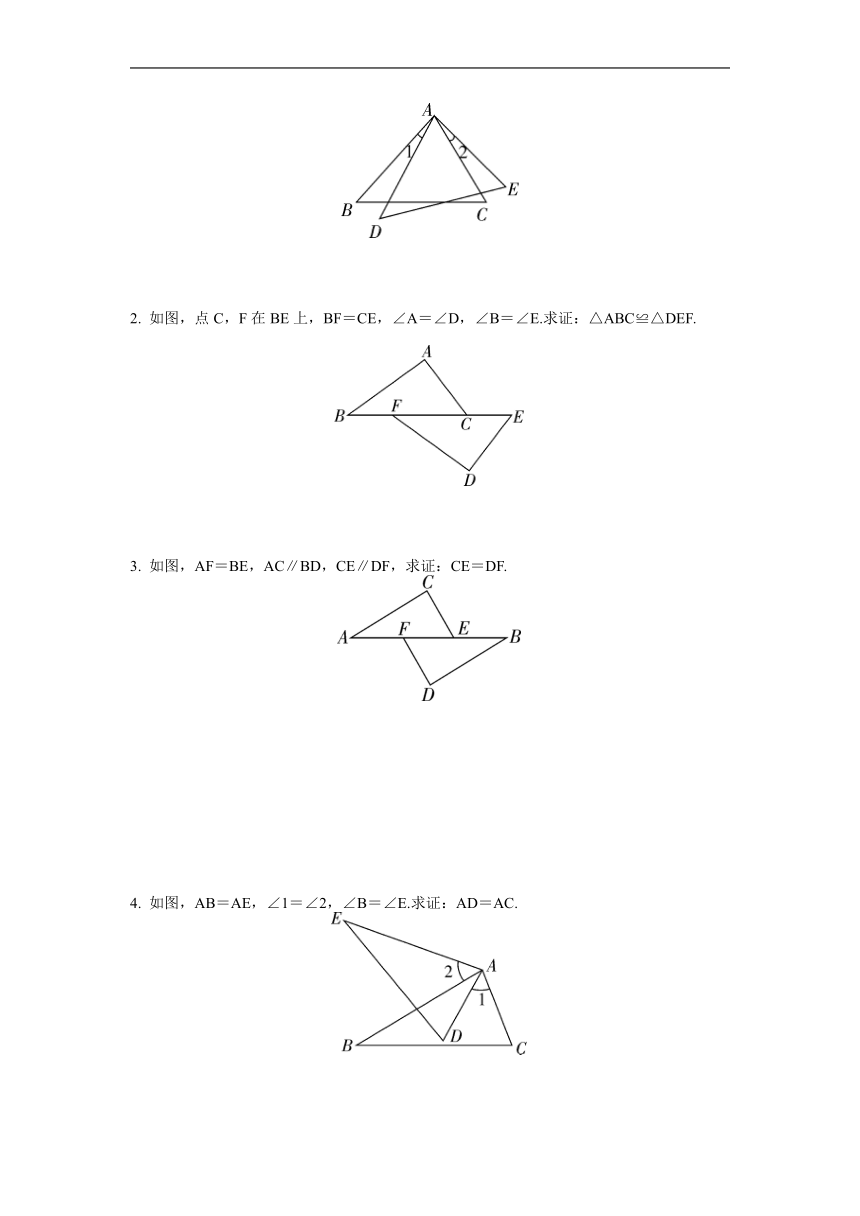
1. 如图,已知∠1=∠2.
(1)当∠3=∠4时,△ABC≌△ABD的依据是 ;
(2)当∠C=∠D时,△ABC≌△ABD的依据是 .
2.如图,BC∥EF,AC∥DF,添加一个条件 ,使得△ABC≌△DEF.
3.如图,在四边形ABCD中,AB∥CD,若用“ASA”证明△ABC≌△CDA,需添加条件 .
4.如图,已知∠ABC=∠DCB,添加下列条件:①AB=CD;②AC=DB;③∠A=∠D;④∠ABO
=∠DCO,能判定△ABC≌△DCB的是 .(填正确答案的序号)
三.解答题
1. 如图,在△ABC和△ADE中,AB=AD,∠B=∠D,∠1=∠2.求证:△ABC≌△ADE.
2. 如图,点C,F在BE上,BF=CE,∠A=∠D,∠B=∠E.求证:△ABC≌△DEF.
3. 如图,AF=BE,AC∥BD,CE∥DF,求证:CE=DF.
4. 如图,AB=AE,∠1=∠2,∠B=∠E.求证:AD=AC.
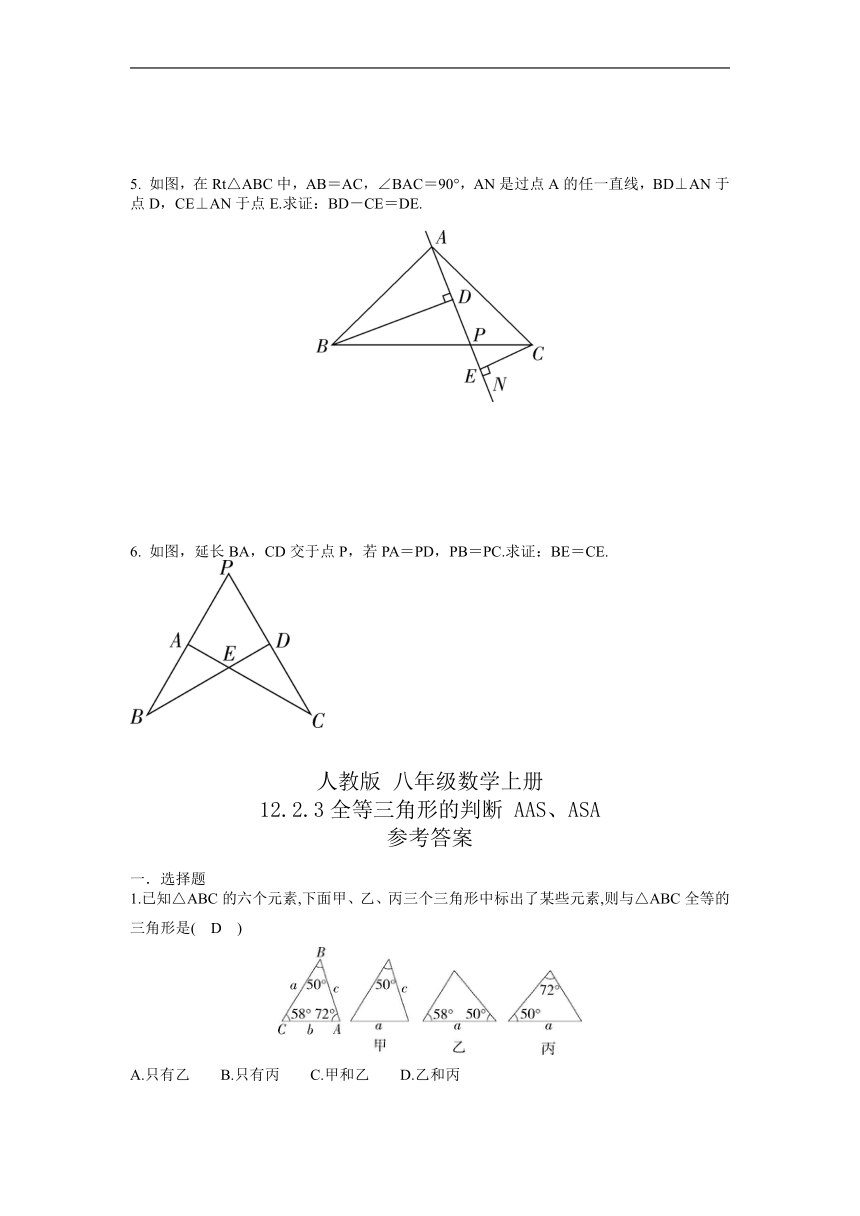
5. 如图,在Rt△ABC中,AB=AC,∠BAC=90°,AN是过点A的任一直线,BD⊥AN于点D,CE⊥AN于点E.求证:BD-CE=DE.
6. 如图,延长BA,CD交于点P,若PA=PD,PB=PC.求证:BE=CE.
人教版 八年级数学上册
12.2.3全等三角形的判断 AAS、ASA
参考答案
一.选择题
1.已知△ABC的六个元素,下面甲、乙、丙三个三角形中标出了某些元素,则与△ABC全等的三角形是( D )
A.只有乙 B.只有丙 C.甲和乙 D.乙和丙
2.如图,∠1=∠2,∠3=∠4,则判定△ABD和△ACD全等的依据是( B )
A.SSS B.ASA C.SAS D.AAS
3.如图,在△ABC和△DEF中,已知∠BCA=∠EFD,∠B=∠E,要判定这两个三角形全等,还需要条件( D )
A.∠A=∠D B.AB=FD
C.AC=ED D.BC=EF
4.如图,AD∥BC,AB∥DC,AC与BD相交于点O,EF经过点O,且与边AD、BC分别交于E、F两点,若BF=DE,则图中的全等三角形有( D )
A.2对 B.3对 C.4对 D.6对
5.如图,已知点B,E,C,F在一条直线上,AC=DF,∠ACB=∠DFE,要使△ABC≌△DEF,不可以添加的条件是( D )
A.BE=CF B.∠A=∠D
C.∠B=∠DEF D.AB=DE
二.填空题
1. 如图,已知∠1=∠2.
(1)当∠3=∠4时,△ABC≌△ABD的依据是 ASA ;
(2)当∠C=∠D时,△ABC≌△ABD的依据是 AAS .
2.如图,BC∥EF,AC∥DF,添加一个条件 AB=DE或BC=EF或AC=DF或AD=BE ,使得△ABC≌△DEF.
3.如图,在四边形ABCD中,AB∥CD,若用“ASA”证明△ABC≌△CDA,需添加条件 ∠ACB=∠CAD(答案不唯一) (填写一个即可).
4.如图,已知∠ABC=∠DCB,添加下列条件:①AB=CD;②AC=DB;③∠A=∠D;④∠ABO
=∠DCO,能判定△ABC≌△DCB的是 ①③④ .(填正确答案的序号)
三.解答题
1. 如图,在△ABC和△ADE中,AB=AD,∠B=∠D,∠1=∠2.求证:△ABC≌△ADE.
证明:∵∠1=∠2,
∴∠1+∠DAC=∠2+∠DAC.
∴∠BAC=∠DAE.
在△ABC和△ADE中,
∴△ABC≌△ADE(ASA).
2. 如图,点C,F在BE上,BF=CE,∠A=∠D,∠B=∠E.求证:△ABC≌△DEF.
证明:∵BF=CE,∴BF+FC=CE+FC,即BC=EF.
在△ABC和△DEF中,
∴△ABC≌△DEF(AAS).
3. 如图,AF=BE,AC∥BD,CE∥DF,求证:CE=DF.
证明:∵AC∥BD,CE∥DF,
∴∠A=∠B,∠CEA=∠DFB.
∵AF=BE,∴AF+EF=BE+EF.
∴AE=BF.
在△AEC和△BFD中,
∴△AEC≌△BFD(ASA).∴CE=DF.
4. 如图,AB=AE,∠1=∠2,∠B=∠E.求证:AD=AC.
证明:∵∠1=∠2,
∴∠1+∠BAD=∠2+∠BAD,
即∠EAD=∠BAC.
在△AED和△ABC中,
∴△AED≌△ABC(ASA).∴AD=AC.
5. 如图,在Rt△ABC中,AB=AC,∠BAC=90°,AN是过点A的任一直线,BD⊥AN于点D,CE⊥AN于点E.求证:BD-CE=DE.
证明:∵BD⊥AN,CE⊥AN,
∴∠ADB=∠CEA=90°.
∵∠BAC=90°,
∴∠BAD+∠CAE=∠CAE+
∠ACE=90°.
∴∠BAD=∠ACE.
在△ABD和△CAE中,
∴△ABD≌△CAE(AAS).
∴BD=AE,AD=CE.
∵AE-AD=DE,∴BD-CE=DE.
6. 如图,延长BA,CD交于点P,若PA=PD,PB=PC.求证:BE=CE.
证明:在△PBD与△PCA中,
∴△PBD≌△PCA(SAS).
∴∠B=∠C.
又由PA=PD,PB=PC,得AB=DC,
∴在△ABE与△DCE中,
∴△ABE≌△DCE(AAS).∴BE=CE.
12.2.3全等三角形的判断 AAS、ASA
一.选择题
1.已知△ABC的六个元素,下面甲、乙、丙三个三角形中标出了某些元素,则与△ABC全等的三角形是( )
A.只有乙 B.只有丙 C.甲和乙 D.乙和丙
2.如图,∠1=∠2,∠3=∠4,则判定△ABD和△ACD全等的依据是( )
A.SSS B.ASA C.SAS D.AAS
3.如图,在△ABC和△DEF中,已知∠BCA=∠EFD,∠B=∠E,要判定这两个三角形全等,还需要条件( )
A.∠A=∠D B.AB=FD
C.AC=ED D.BC=EF
4.如图,AD∥BC,AB∥DC,AC与BD相交于点O,EF经过点O,且与边AD、BC分别交于E、F两点,若BF=DE,则图中的全等三角形有( )
A.2对 B.3对 C.4对 D.6对
5.如图,已知点B,E,C,F在一条直线上,AC=DF,∠ACB=∠DFE,要使△ABC≌△DEF,不可以添加的条件是( )
A.BE=CF B.∠A=∠D
C.∠B=∠DEF D.AB=DE
二.填空题
1. 如图,已知∠1=∠2.
(1)当∠3=∠4时,△ABC≌△ABD的依据是 ;
(2)当∠C=∠D时,△ABC≌△ABD的依据是 .
2.如图,BC∥EF,AC∥DF,添加一个条件 ,使得△ABC≌△DEF.
3.如图,在四边形ABCD中,AB∥CD,若用“ASA”证明△ABC≌△CDA,需添加条件 .
4.如图,已知∠ABC=∠DCB,添加下列条件:①AB=CD;②AC=DB;③∠A=∠D;④∠ABO
=∠DCO,能判定△ABC≌△DCB的是 .(填正确答案的序号)
三.解答题
1. 如图,在△ABC和△ADE中,AB=AD,∠B=∠D,∠1=∠2.求证:△ABC≌△ADE.
2. 如图,点C,F在BE上,BF=CE,∠A=∠D,∠B=∠E.求证:△ABC≌△DEF.
3. 如图,AF=BE,AC∥BD,CE∥DF,求证:CE=DF.
4. 如图,AB=AE,∠1=∠2,∠B=∠E.求证:AD=AC.
5. 如图,在Rt△ABC中,AB=AC,∠BAC=90°,AN是过点A的任一直线,BD⊥AN于点D,CE⊥AN于点E.求证:BD-CE=DE.
6. 如图,延长BA,CD交于点P,若PA=PD,PB=PC.求证:BE=CE.
人教版 八年级数学上册
12.2.3全等三角形的判断 AAS、ASA
参考答案
一.选择题
1.已知△ABC的六个元素,下面甲、乙、丙三个三角形中标出了某些元素,则与△ABC全等的三角形是( D )
A.只有乙 B.只有丙 C.甲和乙 D.乙和丙
2.如图,∠1=∠2,∠3=∠4,则判定△ABD和△ACD全等的依据是( B )
A.SSS B.ASA C.SAS D.AAS
3.如图,在△ABC和△DEF中,已知∠BCA=∠EFD,∠B=∠E,要判定这两个三角形全等,还需要条件( D )
A.∠A=∠D B.AB=FD
C.AC=ED D.BC=EF
4.如图,AD∥BC,AB∥DC,AC与BD相交于点O,EF经过点O,且与边AD、BC分别交于E、F两点,若BF=DE,则图中的全等三角形有( D )
A.2对 B.3对 C.4对 D.6对
5.如图,已知点B,E,C,F在一条直线上,AC=DF,∠ACB=∠DFE,要使△ABC≌△DEF,不可以添加的条件是( D )
A.BE=CF B.∠A=∠D
C.∠B=∠DEF D.AB=DE
二.填空题
1. 如图,已知∠1=∠2.
(1)当∠3=∠4时,△ABC≌△ABD的依据是 ASA ;
(2)当∠C=∠D时,△ABC≌△ABD的依据是 AAS .
2.如图,BC∥EF,AC∥DF,添加一个条件 AB=DE或BC=EF或AC=DF或AD=BE ,使得△ABC≌△DEF.
3.如图,在四边形ABCD中,AB∥CD,若用“ASA”证明△ABC≌△CDA,需添加条件 ∠ACB=∠CAD(答案不唯一) (填写一个即可).
4.如图,已知∠ABC=∠DCB,添加下列条件:①AB=CD;②AC=DB;③∠A=∠D;④∠ABO
=∠DCO,能判定△ABC≌△DCB的是 ①③④ .(填正确答案的序号)
三.解答题
1. 如图,在△ABC和△ADE中,AB=AD,∠B=∠D,∠1=∠2.求证:△ABC≌△ADE.
证明:∵∠1=∠2,
∴∠1+∠DAC=∠2+∠DAC.
∴∠BAC=∠DAE.
在△ABC和△ADE中,
∴△ABC≌△ADE(ASA).
2. 如图,点C,F在BE上,BF=CE,∠A=∠D,∠B=∠E.求证:△ABC≌△DEF.
证明:∵BF=CE,∴BF+FC=CE+FC,即BC=EF.
在△ABC和△DEF中,
∴△ABC≌△DEF(AAS).
3. 如图,AF=BE,AC∥BD,CE∥DF,求证:CE=DF.
证明:∵AC∥BD,CE∥DF,
∴∠A=∠B,∠CEA=∠DFB.
∵AF=BE,∴AF+EF=BE+EF.
∴AE=BF.
在△AEC和△BFD中,
∴△AEC≌△BFD(ASA).∴CE=DF.
4. 如图,AB=AE,∠1=∠2,∠B=∠E.求证:AD=AC.
证明:∵∠1=∠2,
∴∠1+∠BAD=∠2+∠BAD,
即∠EAD=∠BAC.
在△AED和△ABC中,
∴△AED≌△ABC(ASA).∴AD=AC.
5. 如图,在Rt△ABC中,AB=AC,∠BAC=90°,AN是过点A的任一直线,BD⊥AN于点D,CE⊥AN于点E.求证:BD-CE=DE.
证明:∵BD⊥AN,CE⊥AN,
∴∠ADB=∠CEA=90°.
∵∠BAC=90°,
∴∠BAD+∠CAE=∠CAE+
∠ACE=90°.
∴∠BAD=∠ACE.
在△ABD和△CAE中,
∴△ABD≌△CAE(AAS).
∴BD=AE,AD=CE.
∵AE-AD=DE,∴BD-CE=DE.
6. 如图,延长BA,CD交于点P,若PA=PD,PB=PC.求证:BE=CE.
证明:在△PBD与△PCA中,
∴△PBD≌△PCA(SAS).
∴∠B=∠C.
又由PA=PD,PB=PC,得AB=DC,
∴在△ABE与△DCE中,
∴△ABE≌△DCE(AAS).∴BE=CE.
