2022-2023学年人教版九年级数学上册21.3实际问题与一元二次方程 解答题专题提升训练(word、含解析)
文档属性
| 名称 | 2022-2023学年人教版九年级数学上册21.3实际问题与一元二次方程 解答题专题提升训练(word、含解析) | 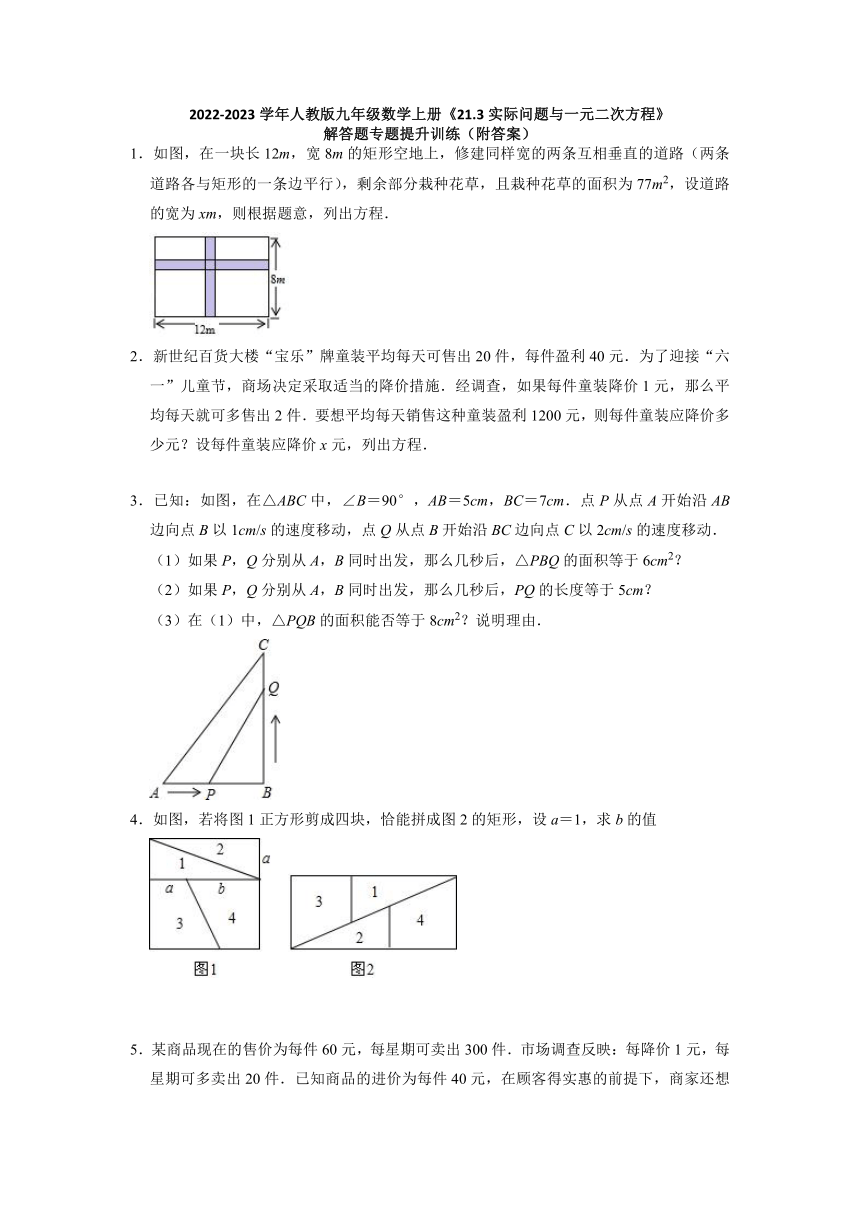 | |
| 格式 | docx | ||
| 文件大小 | 176.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-21 18:37:16 | ||
图片预览





文档简介
2022-2023学年人教版九年级数学上册《21.3实际问题与一元二次方程》
解答题专题提升训练(附答案)
1.如图,在一块长12m,宽8m的矩形空地上,修建同样宽的两条互相垂直的道路(两条道路各与矩形的一条边平行),剩余部分栽种花草,且栽种花草的面积为77m2,设道路的宽为xm,则根据题意,列出方程.
2.新世纪百货大楼“宝乐”牌童装平均每天可售出20件,每件盈利40元.为了迎接“六一”儿童节,商场决定采取适当的降价措施.经调查,如果每件童装降价1元,那么平均每天就可多售出2件.要想平均每天销售这种童装盈利1200元,则每件童装应降价多少元?设每件童装应降价x元,列出方程.
3.已知:如图,在△ABC中,∠B=90°,AB=5cm,BC=7cm.点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动.
(1)如果P,Q分别从A,B同时出发,那么几秒后,△PBQ的面积等于6cm2?
(2)如果P,Q分别从A,B同时出发,那么几秒后,PQ的长度等于5cm?
(3)在(1)中,△PQB的面积能否等于8cm2?说明理由.
4.如图,若将图1正方形剪成四块,恰能拼成图2的矩形,设a=1,求b的值
5.某商品现在的售价为每件60元,每星期可卖出300件.市场调查反映:每降价1元,每星期可多卖出20件.已知商品的进价为每件40元,在顾客得实惠的前提下,商家还想获得6080元的利润,应将销售单价定为多少元?
6.已知关于x的一元二次方程(a+c)x2+2bx+(a﹣c)=0,其中a、b、c分别为△ABC三边的长.
(1)如果x=﹣1是方程的根,试判断△ABC的形状,并说明理由;
(2)如果方程有两个相等的实数根,试判断△ABC的形状,并说明理由;
(3)如果△ABC是等边三角形,试求这个一元二次方程的根.
7.水果店张阿姨以每斤2元的价格购进某种水果若干斤,然后以每斤4元的价格出售,每天可售出100斤,通过调查发现,这种水果每斤的售价每降低0.1元,每天可多售出20斤,为保证每天至少售出260斤,张阿姨决定降价销售.
(1)若将这种水果每斤的售价降低x元,则每天的销售量是 斤(用含x的代数式表示);
(2)销售这种水果要想每天盈利300元,张阿姨需将每斤的售价降低多少元?
8.如图,一农户要建一个矩形猪舍,猪舍的一边利用长为12m的住房墙,另外三边用25m长的建筑材料围成,为方便进出,在垂直于住房墙的一边留一个1m宽的门,所围矩形猪舍的长、宽分别为多少时,猪舍面积为80m2?
9.等腰△ABC的直角边AB=BC=10cm,点P、Q分别从A、C两点同时出发,均以1cm/秒的相同速度作直线运动,已知P沿射线AB运动,Q沿边BC的延长线运动,PQ与直线AC相交于点D.设P点运动时间为t,△PCQ的面积为S.
(1)求出S关于t的函数关系式;
(2)当点P运动几秒时,S△PCQ=S△ABC?
(3)作PE⊥AC于点E,当点P、Q运动时,线段DE的长度是否改变?证明你的结论.
10.某地区2020年投入教育经费2500万元,2022年投入教育经费3025万元.
(1)求2020年至2022年该地区投入教育经费的年平均增长率;
(2)根据(1)所得的年平均增长率,预计2023年该地区将投入教育经费多少万元.
11.列方程解应用题:
某玩具厂生产一种玩具,按照控制固定成本降价促销的原则,使生产的玩具能够及时售出,据市场调查:每个玩具按480元销售时,每天可销售160个;若销售单价每降低1元,每天可多售出2个.已知每个玩具的固定成本为360元,问这种玩具的销售单价为多少元时,厂家每天可获利润20000元?
12.山西特产专卖店销售核桃,其进价为每千克40元,按每千克60元出售,平均每天可售出100千克,后来经过市场调查发现,单价每降低2元,则平均每天的销售可增加20千克,若该专卖店销售这种核桃要想平均每天获利2240元,请回答:
(1)每千克核桃应降价多少元?
(2)在平均每天获利不变的情况下,为尽可能让利于顾客,赢得市场,该店应按原售价的几折出售?
13.现代互联网技术的广泛应用,催生了快递行业的高度发展,据调查,长沙市某家小型“大学生自主创业”的快递公司,今年三月份与五月份完成投递的快递总件数分别为10万件和12.1万件,现假定该公司每月投递的快递总件数的增长率相同.
(1)求该快递公司投递总件数的月平均增长率;
(2)如果平均每人每月最多可投递0.6万件,那么该公司现有的21名快递投递业务员能否完成今年6月份的快递投递任务?如果不能,请问至少需要增加几名业务员?
14.2013年,东营市某楼盘以每平方米6500元的均价对外销售,因为楼盘滞销,房地产开发商为了加快资金周转,决定进行降价促销,经过连续两年下调后,2015年的均价为每平方米5265元.
(1)求平均每年下调的百分率;
(2)假设2016年的均价仍然下调相同的百分率,张强准备购买一套100平方米的住房,他持有现金20万元,可以在银行贷款30万元,张强的愿望能否实现?(房价每平方米按照均价计算)
15.安顺市某商贸公司以每千克40元的价格购进一种干果,计划以每千克60元的价格销售,为了让顾客得到更大的实惠,现决定降价销售,已知这种干果销售量y(千克)与每千克降价x(元)(0<x<20)之间满足一次函数关系,其图象如图所示:
(1)求y与x之间的函数关系式;
(2)商贸公司要想获利2090元,则这种干果每千克应降价多少元?
16.如图,A、B、C、D为矩形的四个顶点,AB=16cm,AD=6cm,动点P、Q分别从点A、C同时出发,点P以3cm/s的速度向点B移动,一直到达B为止,点Q以2cm/s的速度向D移动.
(1)P、Q两点从出发开始到几秒时,四边形PBCQ的面积为33cm2;
(2)P、Q两点从出发开始到几秒时,点P和点Q的距离是10cm.
17.端午节期间,某食品店平均每天可卖出300只粽子,卖出1只粽子的利润是1元.经调查发现,零售单价每降0.1元,每天可多卖出100只粽子.为了使每天获取的利润更多,该店决定把零售单价下降m(0<m<1)元.
(1)零售单价下降m元后,该店平均每天可卖出 只粽子,利润为 元.
(2)在不考虑其他因素的条件下,当m定为多少时,才能使该店每天获取的利润是420元并且卖出的粽子更多?
18.一商店销售某种商品,平均每天可售出20件,每件盈利40元.为了扩大销售、增加盈利,该店采取了降价措施,在每件盈利不少于25元的前提下,经过一段时间销售,发现销售单价每降低1元,平均每天可多售出2件.
(1)若降价3元,则平均每天销售数量为 件;
(2)当每件商品降价多少元时,该商店每天销售利润为1200元?
19.为积极响应新旧动能转换,提高公司经济效益,某科技公司近期研发出一种新型高科技设备,每台设备成本价为30万元,经过市场调研发现,每台售价为40万元时,年销售量为600台;每台售价为45万元时,年销售量为550台.假定该设备的年销售量y(单位:台)和销售单价x(单位:万元)成一次函数关系.
(1)求年销售量y与销售单价x的函数关系式;
(2)根据相关规定,此设备的销售单价不得高于70万元,如果该公司想获得10000万元的年利润,则该设备的销售单价应是多少万元?
20.如图,一块长5米宽4米的地毯,为了美观设计了两横、两纵的配色条纹(图中阴影部分),已知配色条纹的宽度相同,所占面积是整个地毯面积的.
(1)求配色条纹的宽度;
(2)如果地毯配色条纹部分每平方米造价200元,其余部分每平方米造价100元,求地毯的总造价.
21.阅读下列材料:求函数的最大值.
解:将原函数转化成x的一元二次方程,得.
∵x为实数,∴△==﹣y+4≥0,∴y≤4.因此,y的最大值为4.
根据材料给你的启示,求函数的最小值.
22.某文具店去年8月底购进了一批文具1160件,预计在9月份进行试销.购进价格为每件10元.若售价为12元/件,则可全部售出.若每涨价0.1元.销售量就减少2件.
(1)求该文具店在9月份销售量不低于1100件,则售价应不高于多少元?
(2)由于销量好,10月份该文具进价比8月底的进价每件增加20%,该店主增加了进货量,并加强了宣传力度,结果10月份的销售量比9月份在(1)的条件下的最低销售量增加了m%,但售价比9月份在(1)的条件下的最高售价减少m%.结果10月份利润达到3388元,求m的值(m>10).
23.某商店准备进一批季节性小家电,单价40元.经市场预测,销售定价为52元时,可售出180个,定价每增加1元,销售量净减少10个;定价每减少1元,销售量净增加10个.因受库存的影响,每批次进货个数不得超过180个,商店若将准备获利2000元,则应进货多少个?定价为多少元?
24.在水果销售旺季,某水果店购进一优质水果,进价为20元/千克,售价不低于20元/千克,且不超过32元/千克,根据销售情况,发现该水果一天的销售量y(千克)与该天的售价x(元/千克)满足如下表所示的一次函数关系.
销售量y(千克) … 34.8 32 29.6 28 …
售价x(元/千克) … 22.6 24 25.2 26 …
(1)某天这种水果的售价为23.5元/千克,求当天该水果的销售量.
(2)如果某天销售这种水果获利150元,那么该天水果的售价为多少元?
25.已知: ABCD的两边AB,AD的长是关于x的方程x2﹣mx+﹣=0的两个实数根.
(1)当m为何值时,四边形ABCD是菱形?求出这时菱形的边长;
(2)若AB的长为2,那么 ABCD的周长是多少?
26.某水果商场经销一种高档水果,原价每千克50元,连续两次降价后每千克32元,若每次下降的百分率相同
(1)求每次下降的百分率;
(2)若每千克盈利10元,每天可售出500千克,经市场调查发现,在进货价不变的情况下,商场决定采取适当的涨价措施,若每千克涨价1元,日销售量将减少20千克,现该商场要保证每天盈利6000元,且要尽快减少库存,那么每千克应涨价多少元?
27.某地2020年为做好“精准扶贫”,投入资金1280万元用于异地安置,并规划投入资金逐年增加,2022年在2020年的基础上增加投入资金1600万元.
(1)从2020年到2022年,该地投入异地安置资金的年平均增长率为多少?
(2)在2022年异地安置的具体实施中,该地计划投入资金不低于500万元用于优先搬迁租房奖励,规定前1000户(含第1000户)每户每天奖励8元,1000户以后每户每天补助5元,按租房400天计算,试求今年该地至少有多少户享受到优先搬迁租房奖励?
28.如图,四边形ACDE是证明勾股定理时用到的一个图形,a,b,c是Rt△ABC和Rt△BED边长,易知,这时我们把关于x的形如的一元二次方程称为“勾系一元二次方程”.
请解决下列问题:
(1)写出一个“勾系一元二次方程”;
(2)求证:关于x的“勾系一元二次方程”必有实数根;
(3)若x=﹣1是“勾系一元二次方程”的一个根,且四边形ACDE的周长是6,求△ABC面积.
29.如图所示,△ABC中,∠B=90°,AB=6cm,BC=8cm.
(1)点P从点A开始沿AB边向B以1cm/s的速度移动,点Q从B点开始沿BC边向点C以2cm/s的速度移动.如果P,Q分别从A,B同时出发,经过几秒,使△PBQ的面积等于8cm2?
(2)点P从点A开始沿AB边向B以1cm/s的速度移动,点Q从B点开始沿BC边向点C以2cm/s的速度移动.如果P,Q分别从A,B同时出发,线段PQ能否将△ABC分成面积相等的两部分?若能,求出运动时间;若不能说明理由.
(3)若P点沿射线AB方向从A点出发以1cm/s的速度移动,点Q沿射线CB方向从C点出发以2cm/s的速度移动,P,Q同时出发,问几秒后,△PBQ的面积为1cm2?
30.楚天汽车销售公司5月份销售某种型号汽车,当月该型号汽车的进价为30万元/辆,若当月销售量超过5辆时,每多售出1辆,所有售出的汽车进价均降低0.1万元/辆.根据市场调查,月销售量不会突破30台.
(1)设当月该型号汽车的销售量为x辆(x≤30,且x为正整数),实际进价为y万元/辆,求y与x的函数关系式;
(2)已知该型号汽车的销售价为32万元/辆,公司计划当月销售利润25万元,那么该月需售出多少辆汽车?(注:销售利润=销售价﹣进价)
参考答案
1.解:∵道路的宽应为x米,
∴由题意得,(12﹣x)(8﹣x)=77,
故答案为:(12﹣x)(8﹣x)=77.
2.解:设每件童装应降价x元,可列方程为:
(40﹣x)(20+2x)=1200.
故答案为:(40﹣x)(20+2x)=1200.
3.解:(1)设 经过x秒以后△PBQ面积为6
×(5﹣x)×2x=6
整理得:x2﹣5x+6=0
解得:x=2或x=3
答:2或3秒后△PBQ的面积等于6cm2
(2)当PQ=5时,在Rt△PBQ中,∵BP2+BQ2=PQ2,
∴(5﹣t)2+(2t)2=52,
5t2﹣10t=0,
t(5t﹣10)=0,
t1=0(舍弃),t2=2,
∴当t=2时,PQ的长度等于5cm.
(3)设经过x秒以后△PBQ面积为8,
×(5﹣x)×2x=8
整理得:x2﹣5x+8=0
△=25﹣32=﹣7<0
∴△PQB的面积不能等于8cm2.
4.解:依题意得(a+b)2=b(b+a+b),
而a=1,
∴b2﹣b﹣1=0,
∴b=,而b不能为负,
∴b=.
故选:B.
5.解:降价x元,则售价为(60﹣x)元,销售量为(300+20x)件,
根据题意得,(60﹣x﹣40)(300+20x)=6080,
解得x1=1,x2=4,
又顾客得实惠,故取x=4,即定价为56元,
答:应将销售单价定为56元.
6.解:(1)△ABC是等腰三角形;
理由:∵x=﹣1是方程的根,
∴(a+c)×(﹣1)2﹣2b+(a﹣c)=0,
∴a+c﹣2b+a﹣c=0,
∴a﹣b=0,
∴a=b,
∴△ABC是等腰三角形;
(2)△ABC是直角三角形;
理由:∵方程有两个相等的实数根,
∴(2b)2﹣4(a+c)(a﹣c)=0,
∴4b2﹣4a2+4c2=0,
∴a2=b2+c2,
∴△ABC是直角三角形;
(3)当△ABC是等边三角形,∴(a+c)x2+2bx+(a﹣c)=0,可整理为:
2ax2+2ax=0,
∴x2+x=0,
解得:x1=0,x2=﹣1.
7.解:(1)将这种水果每斤的售价降低x元,则每天的销售量是100+×20=(100+200x)(斤);
(2)根据题意得:(4﹣2﹣x)(100+200x)=300,
解得:x=或x=1,
当x=时,销售量是100+200×=200<260;
当x=1时,销售量是100+200=300(斤).
∵每天至少售出260斤,
∴x=1.
答:张阿姨需将每斤的售价降低1元.
8.解:设矩形猪舍垂直于住房墙一边长为xm可以得出平行于墙的一边的长为(25﹣2x+1)m,由题意得
x(25﹣2x+1)=80,
化简,得x2﹣13x+40=0,
解得:x1=5,x2=8,
当x=5时,26﹣2x=16>12(舍去),当x=8时,26﹣2x=10<12,
答:所围矩形猪舍的长为10m、宽为8m.
9.解:(1)当t<10秒时,P在线段AB上,此时CQ=t,PB=10﹣t,
∴S=×t(10﹣t)=(10t﹣t2),
当t>10秒时,P在线段AB得延长线上,此时CQ=t,PB=t﹣10,
∴S=×t(t﹣10)=(t2﹣10t).
(2)∵S△ABC=,
∴当t<10秒时,S△PCQ=,
整理得t2﹣10t+100=0,此方程无解,
当t>10秒时,S△PCQ=,
整理得t2﹣10t﹣100=0,解得t=5±5(舍去负值),
∴当点P运动秒时,S△PCQ=S△ABC.
(3)当点P、Q运动时,线段DE的长度不会改变.
证明:过Q作QM⊥AC,交直线AC于点M,
易证△APE≌△QCM,
∴AE=PE=CM=QM=t,
∴四边形PEQM是平行四边形,且DE是对角线EM的一半.
又∵EM=AC=10∴DE=5
∴当点P、Q运动时,线段DE的长度不会改变.
同理,当点P在点B右侧时,DE=5
综上所述,当点P、Q运动时,线段DE的长度不会改变.
10.解:设增长率为x,根据题意2020年为2500(1+x)万元,2022年为2500(1+x)2万元.
则2500(1+x)2=3025,
解得x=0.1=10%,或x=﹣2.1(不合题意舍去).
答:这两年投入教育经费的平均增长率为10%.
(2)3025×(1+10%)=3327.5(万元).
故根据(1)所得的年平均增长率,预计2023年该地区将投入教育经费3327.5万元.
11.解:设销售单价为x元,
由题意,得:(x﹣360)[160+2(480﹣x)]=20000,
整理,得:x2﹣920x+211600=0,
解得:x1=x2=460,
答:这种玩具的销售单价为460元时,厂家每天可获利润20000元.
12.(1)解:设每千克核桃应降价x元. …1分
根据题意,得 (60﹣x﹣40)(100+×20)=2240. …4分
化简,得 x2﹣10x+24=0 解得x1=4,x2=6.…6分
答:每千克核桃应降价4元或6元. …7分
(2)解:由(1)可知每千克核桃可降价4元或6元.
因为要尽可能让利于顾客,所以每千克核桃应降价6元.
此时,售价为:60﹣6=54(元),
设按原售价的m折出售,则有:60×=54,
解得m=9
答:该店应按原售价的九折出售.
13.解:(1)设该快递公司投递总件数的月平均增长率为x,根据题意得
10(1+x)2=12.1,
解得x1=0.1,x2=﹣2.1(不合题意舍去).
答:该快递公司投递总件数的月平均增长率为10%;
(2)今年6月份的快递投递任务是12.1×(1+10%)=13.31(万件).
∵平均每人每月最多可投递0.6万件,
∴21名快递投递业务员能完成的快递投递任务是:0.6×21=12.6<13.31,
∴该公司现有的21名快递投递业务员不能完成今年6月份的快递投递任务
∴需要增加业务员(13.31﹣12.6)÷0.6=1≈2(人).
答:该公司现有的21名快递投递业务员不能完成今年6月份的快递投递任务,至少需要增加2名业务员.
14.解:(1)设平均每年下调的百分率为x,
根据题意得:6500(1﹣x)2=5265,
解得:x1=0.1=10%,x2=1.9(舍去),
则平均每年下调的百分率为10%;
(2)如果下调的百分率相同,2016年的房价为5265×(1﹣10%)=4738.5(元/米2),
则100平方米的住房总房款为100×4738.5=473850=47.385(万元),
∵20+30>47.385,
∴张强的愿望可以实现.
15.解:(1)设一次函数解析式为:y=kx+b
当x=2,y=120;当x=4,y=140;
∴,
解得:,
∴y与x之间的函数关系式为y=10x+100;
(2)由题意得:
(60﹣40﹣x)(10 x+100)=2090,
整理得:x2﹣10x+9=0,
解得:x1=1.x2=9,
∵让顾客得到更大的实惠,
∴x=9,
答:商贸公司要想获利2090元,则这种干果每千克应降价9元.
16.解:(1)设P、Q两点从出发开始到x秒时四边形PBCQ的面积为33cm2,
则PB=(16﹣3x)cm,QC=2xcm,
根据梯形的面积公式得(16﹣3x+2x)×6=33,
解之得x=5,
(2)设P,Q两点从出发经过t秒时,点P,Q间的距离是10cm,
作QE⊥AB,垂足为E,
则QE=AD=6,PQ=10,
∵PA=3t,CQ=BE=2t,
∴PE=AB﹣AP﹣BE=|16﹣5t|,
由勾股定理,得(16﹣5t)2+62=102,
解得t1=4.8,t2=1.6.
答:(1)P、Q两点从出发开始到5秒时四边形PBCQ的面积为33cm2;
(2)从出发到1.6秒或4.8秒时,点P和点Q的距离是10cm.
17.解:(1)零售单价下降m元后,该店平均每天可卖出(300+100×)只粽子,利润为 (1﹣m)(300+100×)元.
(2)令(1﹣m)(300+100×)=420.
化简得,100m2﹣70m+12=0.
即,m2﹣0.7m+0.12=0.
解得m=0.4或m=0.3.
可得,当m=0.4时卖出的粽子更多.
答:当m为0.4时,才能使商店每天销售该粽子获取的利润是420元并且卖出的粽子更多.
18.解:(1)若降价3元,则平均每天销售数量为20+2×3=26件.
故答案为:26;
(2)设每件商品应降价x元时,该商店每天销售利润为1200元.
根据题意,得 (40﹣x)(20+2x)=1200,
整理,得x2﹣30x+200=0,
解得:x1=10,x2=20.
∵要求每件盈利不少于25元,
∴x2=20应舍去,
∴x=10.
答:每件商品应降价10元时,该商店每天销售利润为1200元.
19.解:(1)设年销售量y与销售单价x的函数关系式为y=kx+b(k≠0),
将(40,600)、(45,550)代入y=kx+b,得:
,解得:,
∴年销售量y与销售单价x的函数关系式为y=﹣10x+1000.
(2)设此设备的销售单价为x万元/台,则每台设备的利润为(x﹣30)万元,销售数量为(﹣10x+1000)台,
根据题意得:(x﹣30)(﹣10x+1000)=10000,
整理,得:x2﹣130x+4000=0,
解得:x1=50,x2=80.
∵此设备的销售单价不得高于70万元,
∴x=50.
答:该设备的销售单价应是50万元/台.
20.解:(1)设条纹的宽度为x米.依题意得
2x×5+2x×4﹣4x2=×5×4,
解得:x1=(不符合,舍去),x2=.
答:配色条纹宽度为米.
(2)条纹造价:×5×4×200=850(元)
其余部分造价:(1﹣)×4×5×100=1575(元)
∴总造价为:850+1575=2425(元)
答:地毯的总造价是2425元.
21.解:将原函数转化成x的一元二次方程,得(y﹣3)x2+(2y﹣1)x+y﹣2=0,
∵x为实数,
∴△=(2y﹣1)2﹣4(y﹣3)(y﹣2)=16y﹣23≥0,
∴y≥,
因此y的最小值为.
22.解:(1)设售价应为x元,依题意有
1160﹣≥1100,
解得x≤15.
答:售价应不高于15元.
(2)10月份的进价:10(1+20%)=12(元),
由题意得:
1100(1+m%)[15(1﹣m%)﹣12]=3388,
设m%=t,化简得50t2﹣25t+2=0,
解得:t1=,t2=,
所以m1=40,m2=10,
因为m>10,
所以m=40.
答:m的值为40.
23.解:设每个商品的定价是x元,
由题意,得(x﹣40)[180﹣10(x﹣52)]=2000,
整理,得x2﹣110x+3000=0,
解得x1=50,x2=60.
当x=50时,进货180﹣10(50﹣52)=200个>180个,不符合题意,舍去;
当x=60时,进货180﹣10(60﹣52)=100个<180个,符合题意.
答:当该商品每个定价为60元时,进货100个.
24.解:(1)设y与x之间的函数关系式为y=kx+b,
将(22.6,34.8)、(24,32)代入y=kx+b,
,解得:,
∴y与x之间的函数关系式为y=﹣2x+80.
当x=23.5时,y=﹣2x+80=33.
答:当天该水果的销售量为33千克.
(2)根据题意得:(x﹣20)(﹣2x+80)=150,
解得:x1=35,x2=25.
∵20≤x≤32,
∴x=25.
答:如果某天销售这种水果获利150元,那么该天水果的售价为25元.
25.解:(1)∵四边形ABCD是菱形,
∴AB=AD,
∴Δ=0,即m2﹣4(﹣)=0,
整理得:(m﹣1)2=0,
解得m=1,
当m=1时,原方程为x2﹣x+=0,
解得:x1=x2=0.5,
故当m=1时,四边形ABCD是菱形,菱形的边长是0.5;
(2)把AB=2代入原方程得,m=2.5,
把m=2.5代入原方程得x2﹣2.5x+1=0,解得x1=2,x2=0.5,
∴C ABCD=2×(2+0.5)=5.
26.解:(1)设每次下降的百分率为a,根据题意,得:
50(1﹣a)2=32,
解得:a=1.8(舍)或a=0.2,
答:每次下降的百分率为20%;
(2)设每千克应涨价x元,由题意,得
(10+x)(500﹣20x)=6000,
整理,得 x2﹣15x+50=0,
解得:x1=5,x2=10,
因为要尽快减少库存,所以x=5符合题意.
答:该商场要保证每天盈利6000元,那么每千克应涨价5元.
27.解:(1)设该地投入异地安置资金的年平均增长率为x,根据题意,
得:1280(1+x)2=1280+1600,
解得:x=0.5或x=﹣2.5(舍),
答:从2020年到2022年,该地投入异地安置资金的年平均增长率为50%;
(2)设今年该地有a户享受到优先搬迁租房奖励,根据题意,
得:1000×8×400+(a﹣1000)×5×400≥5000000,
解得:a≥1900,
答:今年该地至少有1900户享受到优先搬迁租房奖励.
28.(1)解:当a=3,b=4,c=5时
勾系一元二次方程为3x2+5x+4=0;
(2)证明:根据题意,得
Δ=(c)2﹣4ab=2c2﹣4ab
∵a2+b2=c2
∴2c2﹣4ab=2(a2+b2)﹣4ab=2(a﹣b)2≥0
即△≥0
∴勾系一元二次方程必有实数根;
(3)解:当x=﹣1时,有a﹣c+b=0,即a+b=c
∵2a+2b+c=6,即2(a+b)+c=6
∴3c=6
∴c=2
∴a2+b2=c2=4,a+b=2
∵(a+b)2=a2+b2+2ab
∴ab=2
∴S△ABC=ab=1.
29.解:(1)设经过x秒,使△PBQ的面积等于8cm2,依题意有
(6﹣x) 2x=8,
解得x1=2,x2=4,
经检验,x1,x2均符合题意.
故经过2秒或4秒,△PBQ的面积等于8cm2;
(2)设经过y秒,线段PQ能否将△ABC分成面积相等的两部分,依题意有
△ABC的面积=×6×8=24,
(6﹣y) 2y=12,
y2﹣6y+12=0,
∵Δ=b2﹣4ac=36﹣4×12=﹣12<0,
∴此方程无实数根,
∴线段PQ不能将△ABC分成面积相等的两部分;
(3)①点P在线段AB上,点Q在线段CB上(0<m≤4),
设经过m秒,依题意有
(6﹣m)(8﹣2m)=1,
m2﹣10m+23=0,
解得m1=5+,m2=5﹣,
经检验,m1=5+不符合题意,舍去,
∴m=5﹣;
②点P在线段AB上,点Q在射线CB上(4<n≤6),
设经过n秒,依题意有
(6﹣n)(2n﹣8)=1,
n2﹣10n+25=0,
解得n1=n2=5,
经检验,n=5符合题意.
③点P在射线AB上,点Q在射线CB上(k>6),
设经过k秒,依题意有
(k﹣6)(2k﹣8)=1,
k2﹣10k+23=0,
解得k1=5+,k2=5﹣,
经检验,k1=5﹣不符合题意,舍去,
∴k=5+;
综上所述,经过(5﹣)秒,5秒,(5+)秒后,△PBQ的面积为1cm2.
30.解:(1)由题意,得
当0<x≤5时
y=30.
当5<x≤30时,
y=30﹣0.1(x﹣5)=﹣0.1x+30.5.
∴y=;
(2)当0<x≤5时,
(32﹣30)×5=10<25,不符合题意,
当5<x≤30时,
[32﹣(﹣0.1x+30.5)]x=25,
解得:x1=﹣25(舍去),x2=10.
答:该月需售出10辆汽车.
解答题专题提升训练(附答案)
1.如图,在一块长12m,宽8m的矩形空地上,修建同样宽的两条互相垂直的道路(两条道路各与矩形的一条边平行),剩余部分栽种花草,且栽种花草的面积为77m2,设道路的宽为xm,则根据题意,列出方程.
2.新世纪百货大楼“宝乐”牌童装平均每天可售出20件,每件盈利40元.为了迎接“六一”儿童节,商场决定采取适当的降价措施.经调查,如果每件童装降价1元,那么平均每天就可多售出2件.要想平均每天销售这种童装盈利1200元,则每件童装应降价多少元?设每件童装应降价x元,列出方程.
3.已知:如图,在△ABC中,∠B=90°,AB=5cm,BC=7cm.点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动.
(1)如果P,Q分别从A,B同时出发,那么几秒后,△PBQ的面积等于6cm2?
(2)如果P,Q分别从A,B同时出发,那么几秒后,PQ的长度等于5cm?
(3)在(1)中,△PQB的面积能否等于8cm2?说明理由.
4.如图,若将图1正方形剪成四块,恰能拼成图2的矩形,设a=1,求b的值
5.某商品现在的售价为每件60元,每星期可卖出300件.市场调查反映:每降价1元,每星期可多卖出20件.已知商品的进价为每件40元,在顾客得实惠的前提下,商家还想获得6080元的利润,应将销售单价定为多少元?
6.已知关于x的一元二次方程(a+c)x2+2bx+(a﹣c)=0,其中a、b、c分别为△ABC三边的长.
(1)如果x=﹣1是方程的根,试判断△ABC的形状,并说明理由;
(2)如果方程有两个相等的实数根,试判断△ABC的形状,并说明理由;
(3)如果△ABC是等边三角形,试求这个一元二次方程的根.
7.水果店张阿姨以每斤2元的价格购进某种水果若干斤,然后以每斤4元的价格出售,每天可售出100斤,通过调查发现,这种水果每斤的售价每降低0.1元,每天可多售出20斤,为保证每天至少售出260斤,张阿姨决定降价销售.
(1)若将这种水果每斤的售价降低x元,则每天的销售量是 斤(用含x的代数式表示);
(2)销售这种水果要想每天盈利300元,张阿姨需将每斤的售价降低多少元?
8.如图,一农户要建一个矩形猪舍,猪舍的一边利用长为12m的住房墙,另外三边用25m长的建筑材料围成,为方便进出,在垂直于住房墙的一边留一个1m宽的门,所围矩形猪舍的长、宽分别为多少时,猪舍面积为80m2?
9.等腰△ABC的直角边AB=BC=10cm,点P、Q分别从A、C两点同时出发,均以1cm/秒的相同速度作直线运动,已知P沿射线AB运动,Q沿边BC的延长线运动,PQ与直线AC相交于点D.设P点运动时间为t,△PCQ的面积为S.
(1)求出S关于t的函数关系式;
(2)当点P运动几秒时,S△PCQ=S△ABC?
(3)作PE⊥AC于点E,当点P、Q运动时,线段DE的长度是否改变?证明你的结论.
10.某地区2020年投入教育经费2500万元,2022年投入教育经费3025万元.
(1)求2020年至2022年该地区投入教育经费的年平均增长率;
(2)根据(1)所得的年平均增长率,预计2023年该地区将投入教育经费多少万元.
11.列方程解应用题:
某玩具厂生产一种玩具,按照控制固定成本降价促销的原则,使生产的玩具能够及时售出,据市场调查:每个玩具按480元销售时,每天可销售160个;若销售单价每降低1元,每天可多售出2个.已知每个玩具的固定成本为360元,问这种玩具的销售单价为多少元时,厂家每天可获利润20000元?
12.山西特产专卖店销售核桃,其进价为每千克40元,按每千克60元出售,平均每天可售出100千克,后来经过市场调查发现,单价每降低2元,则平均每天的销售可增加20千克,若该专卖店销售这种核桃要想平均每天获利2240元,请回答:
(1)每千克核桃应降价多少元?
(2)在平均每天获利不变的情况下,为尽可能让利于顾客,赢得市场,该店应按原售价的几折出售?
13.现代互联网技术的广泛应用,催生了快递行业的高度发展,据调查,长沙市某家小型“大学生自主创业”的快递公司,今年三月份与五月份完成投递的快递总件数分别为10万件和12.1万件,现假定该公司每月投递的快递总件数的增长率相同.
(1)求该快递公司投递总件数的月平均增长率;
(2)如果平均每人每月最多可投递0.6万件,那么该公司现有的21名快递投递业务员能否完成今年6月份的快递投递任务?如果不能,请问至少需要增加几名业务员?
14.2013年,东营市某楼盘以每平方米6500元的均价对外销售,因为楼盘滞销,房地产开发商为了加快资金周转,决定进行降价促销,经过连续两年下调后,2015年的均价为每平方米5265元.
(1)求平均每年下调的百分率;
(2)假设2016年的均价仍然下调相同的百分率,张强准备购买一套100平方米的住房,他持有现金20万元,可以在银行贷款30万元,张强的愿望能否实现?(房价每平方米按照均价计算)
15.安顺市某商贸公司以每千克40元的价格购进一种干果,计划以每千克60元的价格销售,为了让顾客得到更大的实惠,现决定降价销售,已知这种干果销售量y(千克)与每千克降价x(元)(0<x<20)之间满足一次函数关系,其图象如图所示:
(1)求y与x之间的函数关系式;
(2)商贸公司要想获利2090元,则这种干果每千克应降价多少元?
16.如图,A、B、C、D为矩形的四个顶点,AB=16cm,AD=6cm,动点P、Q分别从点A、C同时出发,点P以3cm/s的速度向点B移动,一直到达B为止,点Q以2cm/s的速度向D移动.
(1)P、Q两点从出发开始到几秒时,四边形PBCQ的面积为33cm2;
(2)P、Q两点从出发开始到几秒时,点P和点Q的距离是10cm.
17.端午节期间,某食品店平均每天可卖出300只粽子,卖出1只粽子的利润是1元.经调查发现,零售单价每降0.1元,每天可多卖出100只粽子.为了使每天获取的利润更多,该店决定把零售单价下降m(0<m<1)元.
(1)零售单价下降m元后,该店平均每天可卖出 只粽子,利润为 元.
(2)在不考虑其他因素的条件下,当m定为多少时,才能使该店每天获取的利润是420元并且卖出的粽子更多?
18.一商店销售某种商品,平均每天可售出20件,每件盈利40元.为了扩大销售、增加盈利,该店采取了降价措施,在每件盈利不少于25元的前提下,经过一段时间销售,发现销售单价每降低1元,平均每天可多售出2件.
(1)若降价3元,则平均每天销售数量为 件;
(2)当每件商品降价多少元时,该商店每天销售利润为1200元?
19.为积极响应新旧动能转换,提高公司经济效益,某科技公司近期研发出一种新型高科技设备,每台设备成本价为30万元,经过市场调研发现,每台售价为40万元时,年销售量为600台;每台售价为45万元时,年销售量为550台.假定该设备的年销售量y(单位:台)和销售单价x(单位:万元)成一次函数关系.
(1)求年销售量y与销售单价x的函数关系式;
(2)根据相关规定,此设备的销售单价不得高于70万元,如果该公司想获得10000万元的年利润,则该设备的销售单价应是多少万元?
20.如图,一块长5米宽4米的地毯,为了美观设计了两横、两纵的配色条纹(图中阴影部分),已知配色条纹的宽度相同,所占面积是整个地毯面积的.
(1)求配色条纹的宽度;
(2)如果地毯配色条纹部分每平方米造价200元,其余部分每平方米造价100元,求地毯的总造价.
21.阅读下列材料:求函数的最大值.
解:将原函数转化成x的一元二次方程,得.
∵x为实数,∴△==﹣y+4≥0,∴y≤4.因此,y的最大值为4.
根据材料给你的启示,求函数的最小值.
22.某文具店去年8月底购进了一批文具1160件,预计在9月份进行试销.购进价格为每件10元.若售价为12元/件,则可全部售出.若每涨价0.1元.销售量就减少2件.
(1)求该文具店在9月份销售量不低于1100件,则售价应不高于多少元?
(2)由于销量好,10月份该文具进价比8月底的进价每件增加20%,该店主增加了进货量,并加强了宣传力度,结果10月份的销售量比9月份在(1)的条件下的最低销售量增加了m%,但售价比9月份在(1)的条件下的最高售价减少m%.结果10月份利润达到3388元,求m的值(m>10).
23.某商店准备进一批季节性小家电,单价40元.经市场预测,销售定价为52元时,可售出180个,定价每增加1元,销售量净减少10个;定价每减少1元,销售量净增加10个.因受库存的影响,每批次进货个数不得超过180个,商店若将准备获利2000元,则应进货多少个?定价为多少元?
24.在水果销售旺季,某水果店购进一优质水果,进价为20元/千克,售价不低于20元/千克,且不超过32元/千克,根据销售情况,发现该水果一天的销售量y(千克)与该天的售价x(元/千克)满足如下表所示的一次函数关系.
销售量y(千克) … 34.8 32 29.6 28 …
售价x(元/千克) … 22.6 24 25.2 26 …
(1)某天这种水果的售价为23.5元/千克,求当天该水果的销售量.
(2)如果某天销售这种水果获利150元,那么该天水果的售价为多少元?
25.已知: ABCD的两边AB,AD的长是关于x的方程x2﹣mx+﹣=0的两个实数根.
(1)当m为何值时,四边形ABCD是菱形?求出这时菱形的边长;
(2)若AB的长为2,那么 ABCD的周长是多少?
26.某水果商场经销一种高档水果,原价每千克50元,连续两次降价后每千克32元,若每次下降的百分率相同
(1)求每次下降的百分率;
(2)若每千克盈利10元,每天可售出500千克,经市场调查发现,在进货价不变的情况下,商场决定采取适当的涨价措施,若每千克涨价1元,日销售量将减少20千克,现该商场要保证每天盈利6000元,且要尽快减少库存,那么每千克应涨价多少元?
27.某地2020年为做好“精准扶贫”,投入资金1280万元用于异地安置,并规划投入资金逐年增加,2022年在2020年的基础上增加投入资金1600万元.
(1)从2020年到2022年,该地投入异地安置资金的年平均增长率为多少?
(2)在2022年异地安置的具体实施中,该地计划投入资金不低于500万元用于优先搬迁租房奖励,规定前1000户(含第1000户)每户每天奖励8元,1000户以后每户每天补助5元,按租房400天计算,试求今年该地至少有多少户享受到优先搬迁租房奖励?
28.如图,四边形ACDE是证明勾股定理时用到的一个图形,a,b,c是Rt△ABC和Rt△BED边长,易知,这时我们把关于x的形如的一元二次方程称为“勾系一元二次方程”.
请解决下列问题:
(1)写出一个“勾系一元二次方程”;
(2)求证:关于x的“勾系一元二次方程”必有实数根;
(3)若x=﹣1是“勾系一元二次方程”的一个根,且四边形ACDE的周长是6,求△ABC面积.
29.如图所示,△ABC中,∠B=90°,AB=6cm,BC=8cm.
(1)点P从点A开始沿AB边向B以1cm/s的速度移动,点Q从B点开始沿BC边向点C以2cm/s的速度移动.如果P,Q分别从A,B同时出发,经过几秒,使△PBQ的面积等于8cm2?
(2)点P从点A开始沿AB边向B以1cm/s的速度移动,点Q从B点开始沿BC边向点C以2cm/s的速度移动.如果P,Q分别从A,B同时出发,线段PQ能否将△ABC分成面积相等的两部分?若能,求出运动时间;若不能说明理由.
(3)若P点沿射线AB方向从A点出发以1cm/s的速度移动,点Q沿射线CB方向从C点出发以2cm/s的速度移动,P,Q同时出发,问几秒后,△PBQ的面积为1cm2?
30.楚天汽车销售公司5月份销售某种型号汽车,当月该型号汽车的进价为30万元/辆,若当月销售量超过5辆时,每多售出1辆,所有售出的汽车进价均降低0.1万元/辆.根据市场调查,月销售量不会突破30台.
(1)设当月该型号汽车的销售量为x辆(x≤30,且x为正整数),实际进价为y万元/辆,求y与x的函数关系式;
(2)已知该型号汽车的销售价为32万元/辆,公司计划当月销售利润25万元,那么该月需售出多少辆汽车?(注:销售利润=销售价﹣进价)
参考答案
1.解:∵道路的宽应为x米,
∴由题意得,(12﹣x)(8﹣x)=77,
故答案为:(12﹣x)(8﹣x)=77.
2.解:设每件童装应降价x元,可列方程为:
(40﹣x)(20+2x)=1200.
故答案为:(40﹣x)(20+2x)=1200.
3.解:(1)设 经过x秒以后△PBQ面积为6
×(5﹣x)×2x=6
整理得:x2﹣5x+6=0
解得:x=2或x=3
答:2或3秒后△PBQ的面积等于6cm2
(2)当PQ=5时,在Rt△PBQ中,∵BP2+BQ2=PQ2,
∴(5﹣t)2+(2t)2=52,
5t2﹣10t=0,
t(5t﹣10)=0,
t1=0(舍弃),t2=2,
∴当t=2时,PQ的长度等于5cm.
(3)设经过x秒以后△PBQ面积为8,
×(5﹣x)×2x=8
整理得:x2﹣5x+8=0
△=25﹣32=﹣7<0
∴△PQB的面积不能等于8cm2.
4.解:依题意得(a+b)2=b(b+a+b),
而a=1,
∴b2﹣b﹣1=0,
∴b=,而b不能为负,
∴b=.
故选:B.
5.解:降价x元,则售价为(60﹣x)元,销售量为(300+20x)件,
根据题意得,(60﹣x﹣40)(300+20x)=6080,
解得x1=1,x2=4,
又顾客得实惠,故取x=4,即定价为56元,
答:应将销售单价定为56元.
6.解:(1)△ABC是等腰三角形;
理由:∵x=﹣1是方程的根,
∴(a+c)×(﹣1)2﹣2b+(a﹣c)=0,
∴a+c﹣2b+a﹣c=0,
∴a﹣b=0,
∴a=b,
∴△ABC是等腰三角形;
(2)△ABC是直角三角形;
理由:∵方程有两个相等的实数根,
∴(2b)2﹣4(a+c)(a﹣c)=0,
∴4b2﹣4a2+4c2=0,
∴a2=b2+c2,
∴△ABC是直角三角形;
(3)当△ABC是等边三角形,∴(a+c)x2+2bx+(a﹣c)=0,可整理为:
2ax2+2ax=0,
∴x2+x=0,
解得:x1=0,x2=﹣1.
7.解:(1)将这种水果每斤的售价降低x元,则每天的销售量是100+×20=(100+200x)(斤);
(2)根据题意得:(4﹣2﹣x)(100+200x)=300,
解得:x=或x=1,
当x=时,销售量是100+200×=200<260;
当x=1时,销售量是100+200=300(斤).
∵每天至少售出260斤,
∴x=1.
答:张阿姨需将每斤的售价降低1元.
8.解:设矩形猪舍垂直于住房墙一边长为xm可以得出平行于墙的一边的长为(25﹣2x+1)m,由题意得
x(25﹣2x+1)=80,
化简,得x2﹣13x+40=0,
解得:x1=5,x2=8,
当x=5时,26﹣2x=16>12(舍去),当x=8时,26﹣2x=10<12,
答:所围矩形猪舍的长为10m、宽为8m.
9.解:(1)当t<10秒时,P在线段AB上,此时CQ=t,PB=10﹣t,
∴S=×t(10﹣t)=(10t﹣t2),
当t>10秒时,P在线段AB得延长线上,此时CQ=t,PB=t﹣10,
∴S=×t(t﹣10)=(t2﹣10t).
(2)∵S△ABC=,
∴当t<10秒时,S△PCQ=,
整理得t2﹣10t+100=0,此方程无解,
当t>10秒时,S△PCQ=,
整理得t2﹣10t﹣100=0,解得t=5±5(舍去负值),
∴当点P运动秒时,S△PCQ=S△ABC.
(3)当点P、Q运动时,线段DE的长度不会改变.
证明:过Q作QM⊥AC,交直线AC于点M,
易证△APE≌△QCM,
∴AE=PE=CM=QM=t,
∴四边形PEQM是平行四边形,且DE是对角线EM的一半.
又∵EM=AC=10∴DE=5
∴当点P、Q运动时,线段DE的长度不会改变.
同理,当点P在点B右侧时,DE=5
综上所述,当点P、Q运动时,线段DE的长度不会改变.
10.解:设增长率为x,根据题意2020年为2500(1+x)万元,2022年为2500(1+x)2万元.
则2500(1+x)2=3025,
解得x=0.1=10%,或x=﹣2.1(不合题意舍去).
答:这两年投入教育经费的平均增长率为10%.
(2)3025×(1+10%)=3327.5(万元).
故根据(1)所得的年平均增长率,预计2023年该地区将投入教育经费3327.5万元.
11.解:设销售单价为x元,
由题意,得:(x﹣360)[160+2(480﹣x)]=20000,
整理,得:x2﹣920x+211600=0,
解得:x1=x2=460,
答:这种玩具的销售单价为460元时,厂家每天可获利润20000元.
12.(1)解:设每千克核桃应降价x元. …1分
根据题意,得 (60﹣x﹣40)(100+×20)=2240. …4分
化简,得 x2﹣10x+24=0 解得x1=4,x2=6.…6分
答:每千克核桃应降价4元或6元. …7分
(2)解:由(1)可知每千克核桃可降价4元或6元.
因为要尽可能让利于顾客,所以每千克核桃应降价6元.
此时,售价为:60﹣6=54(元),
设按原售价的m折出售,则有:60×=54,
解得m=9
答:该店应按原售价的九折出售.
13.解:(1)设该快递公司投递总件数的月平均增长率为x,根据题意得
10(1+x)2=12.1,
解得x1=0.1,x2=﹣2.1(不合题意舍去).
答:该快递公司投递总件数的月平均增长率为10%;
(2)今年6月份的快递投递任务是12.1×(1+10%)=13.31(万件).
∵平均每人每月最多可投递0.6万件,
∴21名快递投递业务员能完成的快递投递任务是:0.6×21=12.6<13.31,
∴该公司现有的21名快递投递业务员不能完成今年6月份的快递投递任务
∴需要增加业务员(13.31﹣12.6)÷0.6=1≈2(人).
答:该公司现有的21名快递投递业务员不能完成今年6月份的快递投递任务,至少需要增加2名业务员.
14.解:(1)设平均每年下调的百分率为x,
根据题意得:6500(1﹣x)2=5265,
解得:x1=0.1=10%,x2=1.9(舍去),
则平均每年下调的百分率为10%;
(2)如果下调的百分率相同,2016年的房价为5265×(1﹣10%)=4738.5(元/米2),
则100平方米的住房总房款为100×4738.5=473850=47.385(万元),
∵20+30>47.385,
∴张强的愿望可以实现.
15.解:(1)设一次函数解析式为:y=kx+b
当x=2,y=120;当x=4,y=140;
∴,
解得:,
∴y与x之间的函数关系式为y=10x+100;
(2)由题意得:
(60﹣40﹣x)(10 x+100)=2090,
整理得:x2﹣10x+9=0,
解得:x1=1.x2=9,
∵让顾客得到更大的实惠,
∴x=9,
答:商贸公司要想获利2090元,则这种干果每千克应降价9元.
16.解:(1)设P、Q两点从出发开始到x秒时四边形PBCQ的面积为33cm2,
则PB=(16﹣3x)cm,QC=2xcm,
根据梯形的面积公式得(16﹣3x+2x)×6=33,
解之得x=5,
(2)设P,Q两点从出发经过t秒时,点P,Q间的距离是10cm,
作QE⊥AB,垂足为E,
则QE=AD=6,PQ=10,
∵PA=3t,CQ=BE=2t,
∴PE=AB﹣AP﹣BE=|16﹣5t|,
由勾股定理,得(16﹣5t)2+62=102,
解得t1=4.8,t2=1.6.
答:(1)P、Q两点从出发开始到5秒时四边形PBCQ的面积为33cm2;
(2)从出发到1.6秒或4.8秒时,点P和点Q的距离是10cm.
17.解:(1)零售单价下降m元后,该店平均每天可卖出(300+100×)只粽子,利润为 (1﹣m)(300+100×)元.
(2)令(1﹣m)(300+100×)=420.
化简得,100m2﹣70m+12=0.
即,m2﹣0.7m+0.12=0.
解得m=0.4或m=0.3.
可得,当m=0.4时卖出的粽子更多.
答:当m为0.4时,才能使商店每天销售该粽子获取的利润是420元并且卖出的粽子更多.
18.解:(1)若降价3元,则平均每天销售数量为20+2×3=26件.
故答案为:26;
(2)设每件商品应降价x元时,该商店每天销售利润为1200元.
根据题意,得 (40﹣x)(20+2x)=1200,
整理,得x2﹣30x+200=0,
解得:x1=10,x2=20.
∵要求每件盈利不少于25元,
∴x2=20应舍去,
∴x=10.
答:每件商品应降价10元时,该商店每天销售利润为1200元.
19.解:(1)设年销售量y与销售单价x的函数关系式为y=kx+b(k≠0),
将(40,600)、(45,550)代入y=kx+b,得:
,解得:,
∴年销售量y与销售单价x的函数关系式为y=﹣10x+1000.
(2)设此设备的销售单价为x万元/台,则每台设备的利润为(x﹣30)万元,销售数量为(﹣10x+1000)台,
根据题意得:(x﹣30)(﹣10x+1000)=10000,
整理,得:x2﹣130x+4000=0,
解得:x1=50,x2=80.
∵此设备的销售单价不得高于70万元,
∴x=50.
答:该设备的销售单价应是50万元/台.
20.解:(1)设条纹的宽度为x米.依题意得
2x×5+2x×4﹣4x2=×5×4,
解得:x1=(不符合,舍去),x2=.
答:配色条纹宽度为米.
(2)条纹造价:×5×4×200=850(元)
其余部分造价:(1﹣)×4×5×100=1575(元)
∴总造价为:850+1575=2425(元)
答:地毯的总造价是2425元.
21.解:将原函数转化成x的一元二次方程,得(y﹣3)x2+(2y﹣1)x+y﹣2=0,
∵x为实数,
∴△=(2y﹣1)2﹣4(y﹣3)(y﹣2)=16y﹣23≥0,
∴y≥,
因此y的最小值为.
22.解:(1)设售价应为x元,依题意有
1160﹣≥1100,
解得x≤15.
答:售价应不高于15元.
(2)10月份的进价:10(1+20%)=12(元),
由题意得:
1100(1+m%)[15(1﹣m%)﹣12]=3388,
设m%=t,化简得50t2﹣25t+2=0,
解得:t1=,t2=,
所以m1=40,m2=10,
因为m>10,
所以m=40.
答:m的值为40.
23.解:设每个商品的定价是x元,
由题意,得(x﹣40)[180﹣10(x﹣52)]=2000,
整理,得x2﹣110x+3000=0,
解得x1=50,x2=60.
当x=50时,进货180﹣10(50﹣52)=200个>180个,不符合题意,舍去;
当x=60时,进货180﹣10(60﹣52)=100个<180个,符合题意.
答:当该商品每个定价为60元时,进货100个.
24.解:(1)设y与x之间的函数关系式为y=kx+b,
将(22.6,34.8)、(24,32)代入y=kx+b,
,解得:,
∴y与x之间的函数关系式为y=﹣2x+80.
当x=23.5时,y=﹣2x+80=33.
答:当天该水果的销售量为33千克.
(2)根据题意得:(x﹣20)(﹣2x+80)=150,
解得:x1=35,x2=25.
∵20≤x≤32,
∴x=25.
答:如果某天销售这种水果获利150元,那么该天水果的售价为25元.
25.解:(1)∵四边形ABCD是菱形,
∴AB=AD,
∴Δ=0,即m2﹣4(﹣)=0,
整理得:(m﹣1)2=0,
解得m=1,
当m=1时,原方程为x2﹣x+=0,
解得:x1=x2=0.5,
故当m=1时,四边形ABCD是菱形,菱形的边长是0.5;
(2)把AB=2代入原方程得,m=2.5,
把m=2.5代入原方程得x2﹣2.5x+1=0,解得x1=2,x2=0.5,
∴C ABCD=2×(2+0.5)=5.
26.解:(1)设每次下降的百分率为a,根据题意,得:
50(1﹣a)2=32,
解得:a=1.8(舍)或a=0.2,
答:每次下降的百分率为20%;
(2)设每千克应涨价x元,由题意,得
(10+x)(500﹣20x)=6000,
整理,得 x2﹣15x+50=0,
解得:x1=5,x2=10,
因为要尽快减少库存,所以x=5符合题意.
答:该商场要保证每天盈利6000元,那么每千克应涨价5元.
27.解:(1)设该地投入异地安置资金的年平均增长率为x,根据题意,
得:1280(1+x)2=1280+1600,
解得:x=0.5或x=﹣2.5(舍),
答:从2020年到2022年,该地投入异地安置资金的年平均增长率为50%;
(2)设今年该地有a户享受到优先搬迁租房奖励,根据题意,
得:1000×8×400+(a﹣1000)×5×400≥5000000,
解得:a≥1900,
答:今年该地至少有1900户享受到优先搬迁租房奖励.
28.(1)解:当a=3,b=4,c=5时
勾系一元二次方程为3x2+5x+4=0;
(2)证明:根据题意,得
Δ=(c)2﹣4ab=2c2﹣4ab
∵a2+b2=c2
∴2c2﹣4ab=2(a2+b2)﹣4ab=2(a﹣b)2≥0
即△≥0
∴勾系一元二次方程必有实数根;
(3)解:当x=﹣1时,有a﹣c+b=0,即a+b=c
∵2a+2b+c=6,即2(a+b)+c=6
∴3c=6
∴c=2
∴a2+b2=c2=4,a+b=2
∵(a+b)2=a2+b2+2ab
∴ab=2
∴S△ABC=ab=1.
29.解:(1)设经过x秒,使△PBQ的面积等于8cm2,依题意有
(6﹣x) 2x=8,
解得x1=2,x2=4,
经检验,x1,x2均符合题意.
故经过2秒或4秒,△PBQ的面积等于8cm2;
(2)设经过y秒,线段PQ能否将△ABC分成面积相等的两部分,依题意有
△ABC的面积=×6×8=24,
(6﹣y) 2y=12,
y2﹣6y+12=0,
∵Δ=b2﹣4ac=36﹣4×12=﹣12<0,
∴此方程无实数根,
∴线段PQ不能将△ABC分成面积相等的两部分;
(3)①点P在线段AB上,点Q在线段CB上(0<m≤4),
设经过m秒,依题意有
(6﹣m)(8﹣2m)=1,
m2﹣10m+23=0,
解得m1=5+,m2=5﹣,
经检验,m1=5+不符合题意,舍去,
∴m=5﹣;
②点P在线段AB上,点Q在射线CB上(4<n≤6),
设经过n秒,依题意有
(6﹣n)(2n﹣8)=1,
n2﹣10n+25=0,
解得n1=n2=5,
经检验,n=5符合题意.
③点P在射线AB上,点Q在射线CB上(k>6),
设经过k秒,依题意有
(k﹣6)(2k﹣8)=1,
k2﹣10k+23=0,
解得k1=5+,k2=5﹣,
经检验,k1=5﹣不符合题意,舍去,
∴k=5+;
综上所述,经过(5﹣)秒,5秒,(5+)秒后,△PBQ的面积为1cm2.
30.解:(1)由题意,得
当0<x≤5时
y=30.
当5<x≤30时,
y=30﹣0.1(x﹣5)=﹣0.1x+30.5.
∴y=;
(2)当0<x≤5时,
(32﹣30)×5=10<25,不符合题意,
当5<x≤30时,
[32﹣(﹣0.1x+30.5)]x=25,
解得:x1=﹣25(舍去),x2=10.
答:该月需售出10辆汽车.
同课章节目录
