2022-2023学年人教版数学九年级下册27.1 图形的相似 同步练习(word、含解析)
文档属性
| 名称 | 2022-2023学年人教版数学九年级下册27.1 图形的相似 同步练习(word、含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 418.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-21 00:00:00 | ||
图片预览



文档简介
27.1 图形的相似
一、选择题(共8小题)
1. 在比例尺为 的地图上,如果A,B两地的距离是 厘米,那么这两地的实际距离是
A. 米 B. 米 C. 米 D. 米
2. 下列说法中正确的个数为
①凡正方形都相似;
②凡等腰三角形都相似;
③凡等腰直角三角形都相似;
④两个相似多边形的面积比为 ,则周长的比为 .
A. B. C. D.
3. 下列图形中一定是相似形的是
A. 两个等腰三角形 B. 两个菱形
C. 两个矩形 D. 两个正方形
4. 在 中,点 ,, 分别在边 ,, 上,连接 ,,如果 ,,,那么 的值是
A. B. C. D.
5. 已知点 是线段 的黄金分割点,且 ,则下列比例式能成立的是
A. B. C. D.
6. 已知线段 .按以下步骤作图:
()作以 为端点的射线 (不与线段 所在直线重合);
()在射线 上顺次截取 ;
()连接 ,过点 作 ,交线段 于点 .
根据上述作图过程,下列结论中正确的是
A. B.
C. D.
7. 如图,点 是线段 的中点,,下列结论中,说法错误的是
A. 与 相似 B. 与 相似
C. D.
8. 矩形的两边长分别为 和 ,把它按如图方式分割成三个全等的小矩形,每一个小矩形与原矩形相似,则 的值为
A. B. C. D.
二、填空题(共6小题)
9. 给出以下结论:
①平移前后的两个图形相似;②旋转前后的两个图形相似;③成轴对称的两个图形相似;④放大或缩小前后的两个图形相似.其中正确的是 .
10. 在比例尺为 的地图上,相距 厘米的两地 , 的实际距离为 米.
11. 我们知道:四个角对应相等,四条边对应成比例的两个四边形是相似四边形.如图,已知梯形 中,,,,, 分别是边 , 上的点,且 ,如果四边 与四边形 相似,那么 的值是 .
12. 如图,已知 ,它们分别交直线 , 于点 ,, 和点 ,,,如果 ,,那么线段 的长是 .
13. 如图,已知 ,它们依次交直线 , 于点 ,, 和点 ,,.如果 ,,那么线段 的长是 .
14. 如图,小芸用灯泡 照射一个矩形相框 ,在墙上形成矩形影子 .现测得 ,,相框 的面积为 ,则影子 的面积为 .
三、解答题(共6小题)
15. 如果 能与 ,, 这三个数组成比例,求 的值.
16. 用有向线段(比例尺选用 )表示两个点的位置差别:
()点 在点 的正北 处.
()点 在点 的西北 处.
()点 在点 的北偏东 方向的 处.
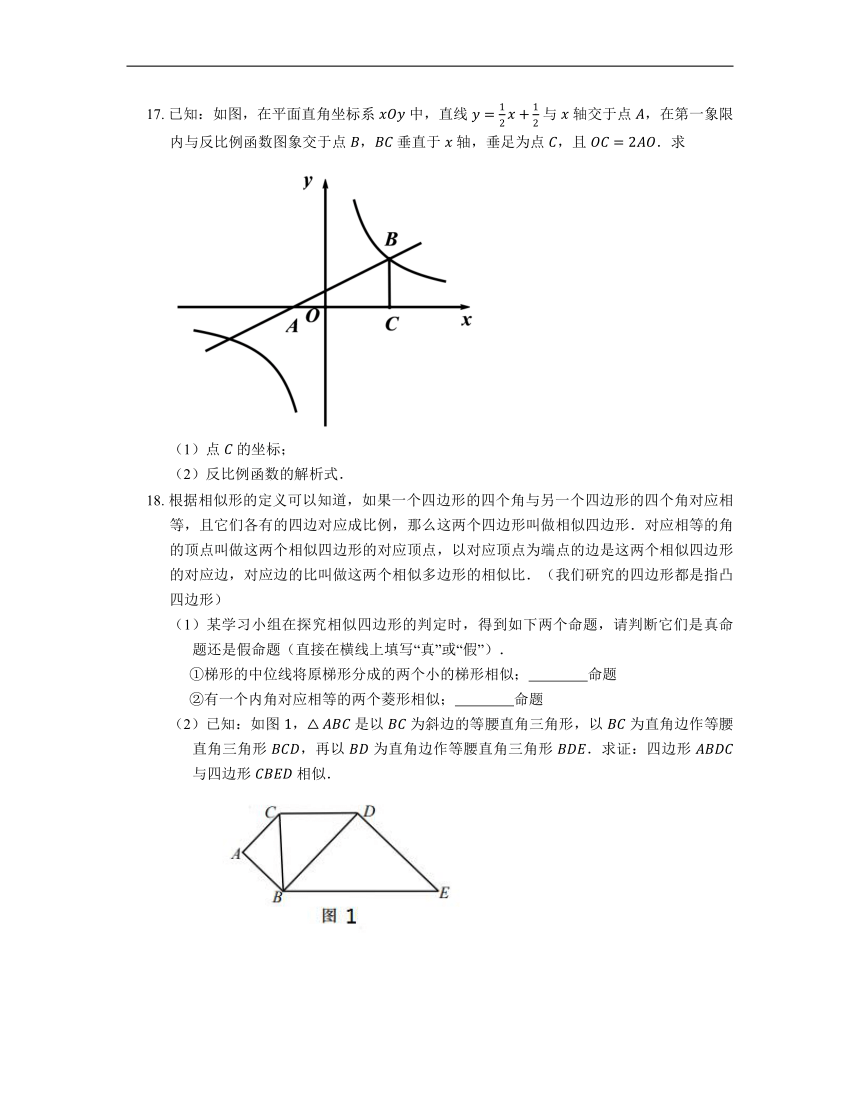
17. 已知:如图,在平面直角坐标系 中,直线 与 轴交于点 ,在第一象限内与反比例函数图象交于点 , 垂直于 轴,垂足为点 ,且 .求
(1)点 的坐标;
(2)反比例函数的解析式.
18. 根据相似形的定义可以知道,如果一个四边形的四个角与另一个四边形的四个角对应相等,且它们各有的四边对应成比例,那么这两个四边形叫做相似四边形.对应相等的角的顶点叫做这两个相似四边形的对应顶点,以对应顶点为端点的边是这两个相似四边形的对应边,对应边的比叫做这两个相似多边形的相似比.(我们研究的四边形都是指凸四边形)
(1)某学习小组在探究相似四边形的判定时,得到如下两个命题,请判断它们是真命题还是假命题(直接在横线上填写“真”或“假”).
①梯形的中位线将原梯形分成的两个小的梯形相似; 命题
②有一个内角对应相等的两个菱形相似; 命题
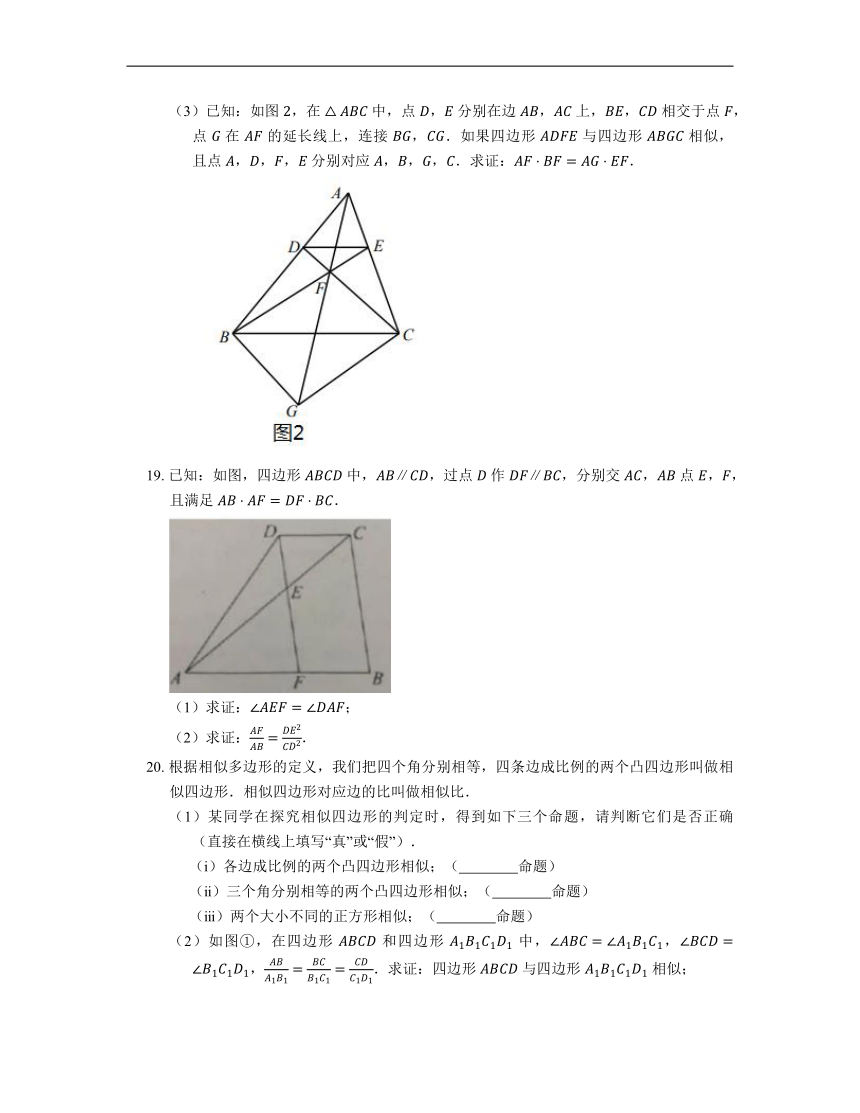
(2)已知:如图 , 是以 为斜边的等腰直角三角形,以 为直角边作等腰直角三角形 ,再以 为直角边作等腰直角三角形 .求证:四边形 与四边形 相似.
(3)已知:如图 ,在 中,点 , 分别在边 , 上,, 相交于点 ,点 在 的延长线上,连接 ,.如果四边形 与四边形 相似,且点 ,,, 分别对应 ,,,.求证:.
19. 已知:如图,四边形 中,,过点 作 ,分别交 , 点 ,,且满足 .
(1)求证:;
(2)求证:.
20. 根据相似多边形的定义,我们把四个角分别相等,四条边成比例的两个凸四边形叫做相似四边形.相似四边形对应边的比叫做相似比.
(1)某同学在探究相似四边形的判定时,得到如下三个命题,请判断它们是否正确(直接在横线上填写“真”或“假”).
(ⅰ)各边成比例的两个凸四边形相似;( 命题)
(ⅱ)三个角分别相等的两个凸四边形相似;( 命题)
(ⅲ)两个大小不同的正方形相似;( 命题)
(2)如图①,在四边形 和四边形 中,,,.求证:四边形 与四边形 相似;
(3)如图②,四边形 中,, 与 相交于点 ,过点 作 分别交 , 于点 ,.记四边形 的面积为 ,四边形 的面积为 ,若四边形 四边形 ,求 的值.
答案
1. C
【解析】根据题意, 厘米 米.
即两地间的实际距离是 米.
故选C.
2. B
【解析】①所有正方形的边成比例,角相等,都相似,故①正确;
②等腰三角形形状不一定相同,所以不一定相似,故②错误;
③所有等腰直角三角形的边成比例,角分别相等,都相似,故③正确;
④两个相似多边形的面积比为 ,则周长的比为 ,故④错误.
所以说法正确的有①③,共 个.
故选B.
3. D
【解析】A、两个等腰三角形,三个角不一定相等,因此不一定相似,故本选项错误,不符合题意.
B、两个菱形对应角不一定相等,故本选项不符合题意;
C、两个矩形的边不一定成比例,故不一定相似,故本选项错误,不符合题意,
D、两个正方形四个角相等,各边一定对应成比例,所以一定相似,故本选项正确,符合题意.
4. B
【解析】如图:
,
,
,
,
.
5. C
【解析】根据黄金分割定义可知: 是 和 的比例中项,即 ,
.
6. C
【解析】作出图形如图.
由题意,得 .
,
,
.
故选:C.
7. D
【解析】,,
,
又 ,
,
故A选项正确;
,
,
为 的中点,
,
,
又 ,
,
故B,C选项正确;
,
,
若 ,则 ,
,
根据现有条件无法判断 ,故 ,
故D选项不正确.
故选:D.
8. B
9. ①②③④
【解析】平移前后、旋转前后、成轴对称的两个图形,放大或缩小前后的两个图形都形状相同,都是相似图形.
10.
【解析】设相距 厘米的两地 , 的实际距离为 厘米,
根据题意得:,
解得:,
经检验, 是上述方程的解,
,
相距 厘米的两地 , 的实际距离为 .
11.
【解析】 四边 与四边形 相似,
,
,,
,
解得:,
四边 与四边形 相似,
.
12.
【解析】,
,
,
又 ,
,
解得 ,
故答案为:.
13.
【解析】,
,
,
设 ,则 ,
,
,
,
解得:,经检验符合题意;
故答案为:.
14.
【解析】由题意可知 ,
,
矩形 的面积:矩形 的面积 ,
又矩形 的面积为 ,则矩形 的面积为 .
15. 或 或
16. 方向按照上北、下南、左西、右东加以区分,长度按比例缩小.
17. (1) 对于直线 ,当 时,得 ,
解得 .
直线 与 轴的交点 的坐标为 .
.
,
.
点 的坐标为 .
(2) 垂直于 轴,
,
,
,
,
设反比例函数的解析式:,
把点 代入得 ,
反比例函数的解析式:.
18. (1) 假;真.
(2) 因为 ,, 是等腰直角三角形,
所以 ,.
所以 ,,,.
设 ,则 ,,.
所以 .
所以四边形 与四边形 相似.
(3) 因为如果四边形 与四边形 相似,且点 ,,, 分别对应 ,,,,
所以 ,.
所以 ,
所以 .
因为 ,
所以 .
所以 ,.
所以 .
所以 .
19. (1) ,
,
,
,
,
,
,
,
.
(2) ,
,
,
,
,
,
,,
四边形 是平行四边形,
,
,
,
,
.
20. (1) (ⅰ)假
(ⅱ)假
(ⅲ)真
(2) 如图,连接 ,,
,且 ,
,
,,,
,
,
,
,
,
,,,
,,
又 ,,,
四边形 与四边形 相似.
(3) 四边形 四边形 ,
,
,
,
,
,,
,
,
,
,
,
,
.
一、选择题(共8小题)
1. 在比例尺为 的地图上,如果A,B两地的距离是 厘米,那么这两地的实际距离是
A. 米 B. 米 C. 米 D. 米
2. 下列说法中正确的个数为
①凡正方形都相似;
②凡等腰三角形都相似;
③凡等腰直角三角形都相似;
④两个相似多边形的面积比为 ,则周长的比为 .
A. B. C. D.
3. 下列图形中一定是相似形的是
A. 两个等腰三角形 B. 两个菱形
C. 两个矩形 D. 两个正方形
4. 在 中,点 ,, 分别在边 ,, 上,连接 ,,如果 ,,,那么 的值是
A. B. C. D.
5. 已知点 是线段 的黄金分割点,且 ,则下列比例式能成立的是
A. B. C. D.
6. 已知线段 .按以下步骤作图:
()作以 为端点的射线 (不与线段 所在直线重合);
()在射线 上顺次截取 ;
()连接 ,过点 作 ,交线段 于点 .
根据上述作图过程,下列结论中正确的是
A. B.
C. D.
7. 如图,点 是线段 的中点,,下列结论中,说法错误的是
A. 与 相似 B. 与 相似
C. D.
8. 矩形的两边长分别为 和 ,把它按如图方式分割成三个全等的小矩形,每一个小矩形与原矩形相似,则 的值为
A. B. C. D.
二、填空题(共6小题)
9. 给出以下结论:
①平移前后的两个图形相似;②旋转前后的两个图形相似;③成轴对称的两个图形相似;④放大或缩小前后的两个图形相似.其中正确的是 .
10. 在比例尺为 的地图上,相距 厘米的两地 , 的实际距离为 米.
11. 我们知道:四个角对应相等,四条边对应成比例的两个四边形是相似四边形.如图,已知梯形 中,,,,, 分别是边 , 上的点,且 ,如果四边 与四边形 相似,那么 的值是 .
12. 如图,已知 ,它们分别交直线 , 于点 ,, 和点 ,,,如果 ,,那么线段 的长是 .
13. 如图,已知 ,它们依次交直线 , 于点 ,, 和点 ,,.如果 ,,那么线段 的长是 .
14. 如图,小芸用灯泡 照射一个矩形相框 ,在墙上形成矩形影子 .现测得 ,,相框 的面积为 ,则影子 的面积为 .
三、解答题(共6小题)
15. 如果 能与 ,, 这三个数组成比例,求 的值.
16. 用有向线段(比例尺选用 )表示两个点的位置差别:
()点 在点 的正北 处.
()点 在点 的西北 处.
()点 在点 的北偏东 方向的 处.
17. 已知:如图,在平面直角坐标系 中,直线 与 轴交于点 ,在第一象限内与反比例函数图象交于点 , 垂直于 轴,垂足为点 ,且 .求
(1)点 的坐标;
(2)反比例函数的解析式.
18. 根据相似形的定义可以知道,如果一个四边形的四个角与另一个四边形的四个角对应相等,且它们各有的四边对应成比例,那么这两个四边形叫做相似四边形.对应相等的角的顶点叫做这两个相似四边形的对应顶点,以对应顶点为端点的边是这两个相似四边形的对应边,对应边的比叫做这两个相似多边形的相似比.(我们研究的四边形都是指凸四边形)
(1)某学习小组在探究相似四边形的判定时,得到如下两个命题,请判断它们是真命题还是假命题(直接在横线上填写“真”或“假”).
①梯形的中位线将原梯形分成的两个小的梯形相似; 命题
②有一个内角对应相等的两个菱形相似; 命题
(2)已知:如图 , 是以 为斜边的等腰直角三角形,以 为直角边作等腰直角三角形 ,再以 为直角边作等腰直角三角形 .求证:四边形 与四边形 相似.
(3)已知:如图 ,在 中,点 , 分别在边 , 上,, 相交于点 ,点 在 的延长线上,连接 ,.如果四边形 与四边形 相似,且点 ,,, 分别对应 ,,,.求证:.
19. 已知:如图,四边形 中,,过点 作 ,分别交 , 点 ,,且满足 .
(1)求证:;
(2)求证:.
20. 根据相似多边形的定义,我们把四个角分别相等,四条边成比例的两个凸四边形叫做相似四边形.相似四边形对应边的比叫做相似比.
(1)某同学在探究相似四边形的判定时,得到如下三个命题,请判断它们是否正确(直接在横线上填写“真”或“假”).
(ⅰ)各边成比例的两个凸四边形相似;( 命题)
(ⅱ)三个角分别相等的两个凸四边形相似;( 命题)
(ⅲ)两个大小不同的正方形相似;( 命题)
(2)如图①,在四边形 和四边形 中,,,.求证:四边形 与四边形 相似;
(3)如图②,四边形 中,, 与 相交于点 ,过点 作 分别交 , 于点 ,.记四边形 的面积为 ,四边形 的面积为 ,若四边形 四边形 ,求 的值.
答案
1. C
【解析】根据题意, 厘米 米.
即两地间的实际距离是 米.
故选C.
2. B
【解析】①所有正方形的边成比例,角相等,都相似,故①正确;
②等腰三角形形状不一定相同,所以不一定相似,故②错误;
③所有等腰直角三角形的边成比例,角分别相等,都相似,故③正确;
④两个相似多边形的面积比为 ,则周长的比为 ,故④错误.
所以说法正确的有①③,共 个.
故选B.
3. D
【解析】A、两个等腰三角形,三个角不一定相等,因此不一定相似,故本选项错误,不符合题意.
B、两个菱形对应角不一定相等,故本选项不符合题意;
C、两个矩形的边不一定成比例,故不一定相似,故本选项错误,不符合题意,
D、两个正方形四个角相等,各边一定对应成比例,所以一定相似,故本选项正确,符合题意.
4. B
【解析】如图:
,
,
,
,
.
5. C
【解析】根据黄金分割定义可知: 是 和 的比例中项,即 ,
.
6. C
【解析】作出图形如图.
由题意,得 .
,
,
.
故选:C.
7. D
【解析】,,
,
又 ,
,
故A选项正确;
,
,
为 的中点,
,
,
又 ,
,
故B,C选项正确;
,
,
若 ,则 ,
,
根据现有条件无法判断 ,故 ,
故D选项不正确.
故选:D.
8. B
9. ①②③④
【解析】平移前后、旋转前后、成轴对称的两个图形,放大或缩小前后的两个图形都形状相同,都是相似图形.
10.
【解析】设相距 厘米的两地 , 的实际距离为 厘米,
根据题意得:,
解得:,
经检验, 是上述方程的解,
,
相距 厘米的两地 , 的实际距离为 .
11.
【解析】 四边 与四边形 相似,
,
,,
,
解得:,
四边 与四边形 相似,
.
12.
【解析】,
,
,
又 ,
,
解得 ,
故答案为:.
13.
【解析】,
,
,
设 ,则 ,
,
,
,
解得:,经检验符合题意;
故答案为:.
14.
【解析】由题意可知 ,
,
矩形 的面积:矩形 的面积 ,
又矩形 的面积为 ,则矩形 的面积为 .
15. 或 或
16. 方向按照上北、下南、左西、右东加以区分,长度按比例缩小.
17. (1) 对于直线 ,当 时,得 ,
解得 .
直线 与 轴的交点 的坐标为 .
.
,
.
点 的坐标为 .
(2) 垂直于 轴,
,
,
,
,
设反比例函数的解析式:,
把点 代入得 ,
反比例函数的解析式:.
18. (1) 假;真.
(2) 因为 ,, 是等腰直角三角形,
所以 ,.
所以 ,,,.
设 ,则 ,,.
所以 .
所以四边形 与四边形 相似.
(3) 因为如果四边形 与四边形 相似,且点 ,,, 分别对应 ,,,,
所以 ,.
所以 ,
所以 .
因为 ,
所以 .
所以 ,.
所以 .
所以 .
19. (1) ,
,
,
,
,
,
,
,
.
(2) ,
,
,
,
,
,
,,
四边形 是平行四边形,
,
,
,
,
.
20. (1) (ⅰ)假
(ⅱ)假
(ⅲ)真
(2) 如图,连接 ,,
,且 ,
,
,,,
,
,
,
,
,
,,,
,,
又 ,,,
四边形 与四边形 相似.
(3) 四边形 四边形 ,
,
,
,
,
,,
,
,
,
,
,
,
.
