2022-2023学年北师大版数学九年级上册 3.2 用频率估计概率 同步练习(Word版含答案)
文档属性
| 名称 | 2022-2023学年北师大版数学九年级上册 3.2 用频率估计概率 同步练习(Word版含答案) | 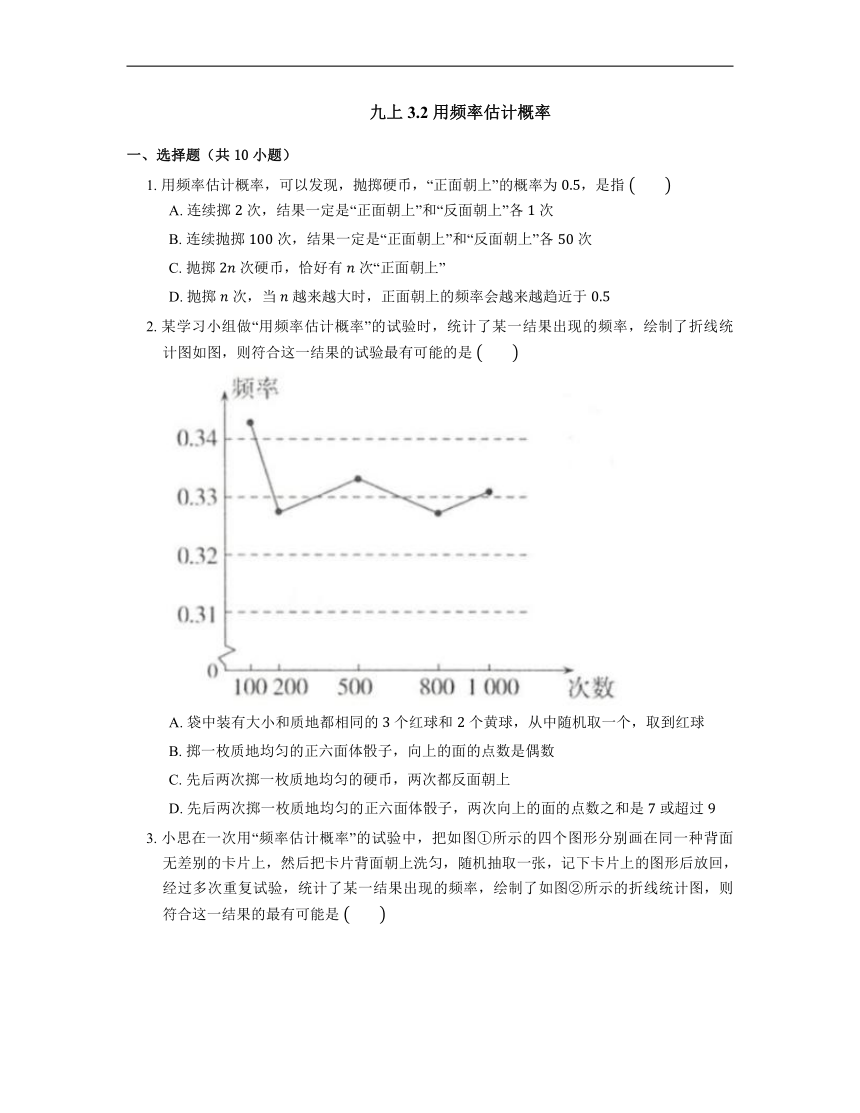 | |
| 格式 | docx | ||
| 文件大小 | 435.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-22 15:01:52 | ||
图片预览





文档简介
九上 3.2 用频率估计概率
一、选择题(共10小题)
1. 用频率估计概率,可以发现,抛掷硬币,“正面朝上”的概率为 ,是指
A. 连续掷 次,结果一定是“正面朝上”和“反面朝上”各 次
B. 连续抛掷 次,结果一定是“正面朝上”和“反面朝上”各 次
C. 抛掷 次硬币,恰好有 次“正面朝上”
D. 抛掷 次,当 越来越大时,正面朝上的频率会越来越趋近于
2. 某学习小组做“用频率估计概率”的试验时,统计了某一结果出现的频率,绘制了折线统计图如图,则符合这一结果的试验最有可能的是
A. 袋中装有大小和质地都相同的 个红球和 个黄球,从中随机取一个,取到红球
B. 掷一枚质地均匀的正六面体骰子,向上的面的点数是偶数
C. 先后两次掷一枚质地均匀的硬币,两次都反面朝上
D. 先后两次掷一枚质地均匀的正六面体骰子,两次向上的面的点数之和是 或超过
3. 小思在一次用“频率估计概率”的试验中,把如图①所示的四个图形分别画在同一种背面无差别的卡片上,然后把卡片背面朝上洗匀,随机抽取一张,记下卡片上的图形后放回,经过多次重复试验,统计了某一结果出现的频率,绘制了如图②所示的折线统计图,则符合这一结果的最有可能是
A. 抽出的是中心对称图形
B. 抽出的是非中心对称图形
C. 抽出的是轴对称图形
D. 抽出的既是中心对称图形也是轴对称图形
4. 在一个不透明的盒子里装有 个红、黄两种颜色的小球,这些球除颜色外其他完全相同,每次摸球前先将盒子里的球摇匀,任意摸出一个球,记下颜色后再放回盒子,通过大量重复试验后发现,摸到黄球的频率稳定在 ,那么估计盒子中黄球的个数为
A. B. C. D.
5. 某班的一个数学兴趣小组为了考察本市某条斑马线上驾驶员礼让行人的情况,每天利用放学时间进行调查,下表是该小组一个月内累计调查的结果,由此结果可估计驾驶员能主动给行人让路的概率为
\[
\begin{array}{|c|c|c|c|c|c|c|} \hline
\hline 抽查车辆数&100&500&1000&2000&3000&4000\\ \hline
\hline 能礼让的驾驶员人数&95&486&968&1940&2907&3880\\ \hline
\hline 能礼让的频率& 0.95 & 0.972 & 0.968 & 0.97 & 0.969 & 0.97 \\ \hline \end{array} \]
A. B. C. D.
6. 用频率估计概率,可以发现,某种幼树在一定条件下移植成活的概率为 ,下列说法正确的是
A. 种植 棵幼树,结果一定是“ 棵幼树成活”
B. 种植 棵幼树,结果一定是“ 棵幼树成活”和“ 棵幼树不成活”
C. 种植 棵幼树,恰好有“ 棵幼树不成活”
D. 种植 棵幼树,当 越来越大时,种植成活幼树的频率会越来越稳定于
7. 下列叙述随机事件的频率与概率的关系中,说法正确的是
A. 频率就是概率 B. 频率是随机的,与试验次数无关
C. 概率是稳定的,与试验次数无关 D. 概率是随机的,与试验次数有关
8. 在大量重复试验中,关于随机事件发生的频率与概率,下列说法正确的是
A. 频率就是概率
B. 频率与试验次数无关
C. 概率是随机的,与频率无关
D. 随着试验次数的增加,频率一般会越来越接近概率
9. 甲、乙两名同学在一次用频率去估计概率的试验中统计了某一结果出现的频率,绘出的统计图如图所示,则符合这一结果的试验可能是
A. 掷一枚正六面体的骰子,出现 点的概率
B. 从一个装有 个白球和 个红球的袋子中任取 球,取到红球的概率
C. 抛一枚硬币,出现正面的概率
D. 任意写一个整数,它能被 整除的概率
10. 如图,正方形 内有一个圆 .电脑可设计程序:在正方形内可随机产生一系列点,当点数很多时,电脑自动统计正方形内的点数 ,圆 内的点数 (在正方形边上和圆上的点不在统计中),利用频率估计概率的原理,可推得 的大小是
A. B. C. D.
二、填空题(共6小题)
11. 年北京冬奥会的吉祥物有两种:冰墩墩和雪容融.在一个不透明的袋子里放有 张吉祥物的卡片,每张卡片写有一种吉祥物的名称,小杰从中任意抽取一张再放回,重复试验 次后,摸到冰墩墩 次.则可估计袋子里写有“雪容融”的卡片数量是 .
12. 蒲丰是十八世纪的法国著名数学家,他发现:在一张白纸上画满距离相等的平行线,将长度为平行线间距离一半的小针随意投掷到纸面上,则小针与直线相交的概率就是圆周率 的倒数.
统计试验数据:共投针 次,其中小针与直线相交的次数有 次.由此可估计 的近似值为 (保留到小数点后第三位).
13. 在一个不透明的布袋中,有黄色、白色的乒乓球共10个,这些球除颜色外都相同.小刚通过多次摸球实验后发现其中摸到黄球的频率稳定在60%,则布袋中白色球的个数很可能是 个.
14. 一个暗箱中装有只有颜色不同的 ()个布娃娃,分别是 个白娃娃、 个绿娃娃, 个红娃娃和 个黄娃娃,从中任意拿出一个布娃娃,记下颜色后放回,经过大量重复试验,把拿出白娃娃,绿娃娃,红娃娃的频率绘制成如图所示的条形统计图(未绘制完整).根据题中给出的信息,暗箱中黄娃娃的个数为 .
15. 如图,在半径为 的 中,随意向圆内投掷一个小球,经过大量重复投掷后发现,小球落在阴影部分的频率稳定在 ,则 的长约为 .(结果保留 )
16. 某水果公司以 元/千克的成本价购进 苹果.公司想知道苹果的损坏率,从所有苹果中随机抽取若干进行统计,部分结果如表:
估计这批苹果损坏的概率为 (精确到 ),据此,若公司希望这批苹果能获得利润 元,则销售时(去掉损坏的苹果)售价应至少定为 元/千克.
三、解答题(共6小题)
17. 在一个不透明的盒子里装有只有颜色不同的黑、白两种球共 个,小明做摸球试验,他将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程,下表是试验中的一组统计数据:
(1)完成表格(除不尽的精确到 ).
(2)请估计当 很大时,摸到白球的频率将会接近 (精确到 ).
(3)试估算盒子里黑、白两种颜色的球各有多少只
18. 通过试验判断:掷一枚图钉,落到地面时,图钉的针尖可能朝上也可能朝下,“针尖朝上”与“针尖朝下”是不是等可能事件
找几个同学先分头进行掷图钉的试验,再合在一起统计试验结果,根据频率估计“针尖朝上”的概率与“针尖朝下”的概率.
19. 小明从一本书中随机抽取了 页,在累计 页至 页中的“的”字和“了”字出现的次数后,分别求出了它们出现的频率,并绘制了如下统计图(如图中页数 对应的频率是三页中累计的结果).
(1)随着统计页数的增加,这两个字出现的频率是如何变化的
(2)你认为该书中的“的”和“了”两个字出现的频率哪个高
20. 小明和小杰为了估计抛掷图钉时针尖朝上的概率,分别做了试验.小明的试验结果记录在表一,小杰的试验结果记录在表二.
表一:
表二:
(1)在小明的试验中,针尖朝上的频率是多少 在小杰的试验中,针尖朝上的频率又是多少
(2)求针尖朝上的概率估计值,并说明理由.
21. 如图 ,一枚扁式图钉由钉帽和钉尖两部分组成.通过试验发现,这枚图钉落在坚硬的地面上,顶尖可能朝下也可能朝上.
(1)请你与一位同伴合作,做抛掷扁式图钉的试验,并将两人的试验结果分别记录如下表(表 ,表 ).
表
表
(2)分别写出你和同伴在试验中钉尖朝上和朝下的频率.
(3)求钉尖朝上的概率估计值.
(4)近年来在中学校园中,更常见的是另一种图钉(如图 ),请从概率的角度解释更换为这种图钉的原因.
22. 新冠疫情期间,某校开展线上教学,有“录播”和“直播”两种教学方式供学生选择其一种.为分析该校学生线上学习情况,在接受这两种教学方式的学生中各随机抽取 人调查学习参与度,数据整理结果如下表(数据分组包含左端值不包含右端值).
(1)你认为哪种教学方式学生的参与度更高 简要说明理由.
(2)从教学方式为“直播”的学生中任意抽取一位学生,估计该学生的参与度在 及以上的概率是多少.
(3)该校共有 名学生,选择“录播”和“直播”的人数之比为 ,估计参与度在 以下的共有多少人.
答案
1. D
2. D
【解析】由题中的折线统计图可知,随着试验次数的增加,该结果出现的频率稳定在 附近,可估计该结果出现的概率为 .袋中装有大小和质地都相同的 个红球和 个黄球,从中随机取一个,取到红球的概率为 ,故A不符合题意;
掷一枚质地均匀的正六面体骰子,向上的面的点数是偶数的概率为 ,故B不符合题意;
先后两次掷一枚质地均匀的硬币,两次都反面朝上的概率为 ,故C不符合题意;
先后两次掷一枚质地均匀的正六面体骰子,两次向上的面的点数之和是 或超过 的概率为 ,故D符合题意.
3. D
【解析】题中 个图形中,中心对称图形有 个,非中心对称图形有 个,轴对称图形有 个,既是中心对称图形又是轴对称图形的有 个.
由题中频率折线统计图可知,该结果出现的频率逐渐稳定在 附近,可估计该结果出现的概率为 .
选项A,抽出的是中心对称图形的概率是 ,不符合题意;
选项B,抽出的是非中心对称图形的概率是 ,不符合题意;
选项C,抽出的是轴对称图形的概率是 ,不符合题意;
选项D,抽出的既是中心对称图形也是轴对称图形的概率是 ,符合题意,
故选D.
4. B
【解析】设盒子中黄球的个数为 ,
通过大量重复试验后发现,摸到黄球的频率稳定在 ,
估计任意摸出一个球,是黄球的概率为 .
根据题意,得 ,
解得 ,
即盒子中黄球的个数为 .
5. C
【解析】由表格可知,随着抽查车辆数逐渐增大,能礼让行人的车辆的频率趋近于 ,
可估计驾驶员能主动给行人让路的概率为 .
6. D
【解析】用频率估计的概率是在大量重复试验中得到的概率的近似值.可知A,B,C错误,D正确.故选D.
7. C
【解析】频率是随机的,随试验而变化,但概率是唯一确定的一个值,在大量重复试验中,随试验次数的增大,频率会逐渐稳定于概率附近.
8. D
【解析】【分析】根据大量重复试验事件发生的频率逐渐稳定到某个常数附近,可以用这个常数估计这个事件发生的概率解答.
【解析】解:大量重复试验事件发生的频率逐渐稳定到某个常数附近,可以用这个常数估计这个事件发生的概率,
选项说法正确.
故选:.
【点评】本题考查了利用频率估计概率的知识,大量重复试验事件发生的频率逐渐稳定到某个常数附近,可以用这个常数估计这个事件发生的概率.
9. B
10. B
【解析】设圆的半径为 ,则正方形的边长为 ,
根据题意得 ,
故 .
11. 张
12.
13. 4
【解析】【分析】设出黄球的个数,根据黄球的频率求出黄球的个数即可解答.
【解析】解:设黄球的个数为,
共有黄色、白色的乒乓球10个,黄球的频率稳定在60%,
≈0.6,
解得,,
布袋中白色球的个数很可能是个.
【点评】考查利用频率估计概率.大量反复试验下频率稳定值即概率.关键是根据黄球的频率得到相应的等量关系.
14.
【解析】由题中条形统计图可知,拿出绿娃娃的频率为 ,估计从中任意拿出一个布娃娃,恰好拿出的是绿娃娃的概率为 ,
,
解得 ,
经检验, 是原分式方程的解,
暗箱中黄娃娃的个数为 .
15.
【解析】 大量重复投掷后发现,小球落在阴影部分的频率稳定在 ,
扇形面积占圆面积的 ,
的长占圆周长的 ,
的长约为 .
16. ,
【解析】根据表中的损坏的频率,当实验次次数的增多时,苹果损坏的频率越来越稳定在 左右,所以苹果的损坏概率为 .
根据估计的概率可以知道,在 苹果中完好苹果的质量为 .
设每千克苹果的销售价为 元,
则应有 ,
解得 .
17. (1)
(2)
(3) ,
.
答:黑球有 个,白球有 个.
18. 略
19. (1) “的”字频率趋近 ,“了”字频率趋近 .
(2) “的”字出现的频率高.
20. (1) 小明的试验中针尖朝上的频率为 ,小杰的试验中针尖朝上的频率为 .
(2) 图钉针尖朝上的概率估计是 ,因为大数次试验的频率才稳定于概率附近.
21. (1) 填表(略);
(2) 过程略;
(3) 过程略,依据第()问的频率,但要注意选择大次数的试验进行计算;
(4) 图 的图钉落下后钉尖朝上的概率接近 ,安全性更高.
22. (1) “直播”教学方式学生的参与度更高.
理由:“直播”参与度在 以上的人数为 ,“录播”参与度在 以上的人数为 ,参与度在 以上的“直播”人数远多于“录播”人数,
所以“直播”教学方式学生的参与度更高.
(2) .
答:估计该学生的参与度在 及以上的概率是 .
(3) 选择“录播”的学生数为 ,选择“直播”的学生数为 ,
所以“录播”参与度在 以下的学生数为 ,“直播”参与度在 以下的学生数为 ,
所以估计参与度在 以下的学生共有 (人).
一、选择题(共10小题)
1. 用频率估计概率,可以发现,抛掷硬币,“正面朝上”的概率为 ,是指
A. 连续掷 次,结果一定是“正面朝上”和“反面朝上”各 次
B. 连续抛掷 次,结果一定是“正面朝上”和“反面朝上”各 次
C. 抛掷 次硬币,恰好有 次“正面朝上”
D. 抛掷 次,当 越来越大时,正面朝上的频率会越来越趋近于
2. 某学习小组做“用频率估计概率”的试验时,统计了某一结果出现的频率,绘制了折线统计图如图,则符合这一结果的试验最有可能的是
A. 袋中装有大小和质地都相同的 个红球和 个黄球,从中随机取一个,取到红球
B. 掷一枚质地均匀的正六面体骰子,向上的面的点数是偶数
C. 先后两次掷一枚质地均匀的硬币,两次都反面朝上
D. 先后两次掷一枚质地均匀的正六面体骰子,两次向上的面的点数之和是 或超过
3. 小思在一次用“频率估计概率”的试验中,把如图①所示的四个图形分别画在同一种背面无差别的卡片上,然后把卡片背面朝上洗匀,随机抽取一张,记下卡片上的图形后放回,经过多次重复试验,统计了某一结果出现的频率,绘制了如图②所示的折线统计图,则符合这一结果的最有可能是
A. 抽出的是中心对称图形
B. 抽出的是非中心对称图形
C. 抽出的是轴对称图形
D. 抽出的既是中心对称图形也是轴对称图形
4. 在一个不透明的盒子里装有 个红、黄两种颜色的小球,这些球除颜色外其他完全相同,每次摸球前先将盒子里的球摇匀,任意摸出一个球,记下颜色后再放回盒子,通过大量重复试验后发现,摸到黄球的频率稳定在 ,那么估计盒子中黄球的个数为
A. B. C. D.
5. 某班的一个数学兴趣小组为了考察本市某条斑马线上驾驶员礼让行人的情况,每天利用放学时间进行调查,下表是该小组一个月内累计调查的结果,由此结果可估计驾驶员能主动给行人让路的概率为
\[
\begin{array}{|c|c|c|c|c|c|c|} \hline
\hline 抽查车辆数&100&500&1000&2000&3000&4000\\ \hline
\hline 能礼让的驾驶员人数&95&486&968&1940&2907&3880\\ \hline
\hline 能礼让的频率& 0.95 & 0.972 & 0.968 & 0.97 & 0.969 & 0.97 \\ \hline \end{array} \]
A. B. C. D.
6. 用频率估计概率,可以发现,某种幼树在一定条件下移植成活的概率为 ,下列说法正确的是
A. 种植 棵幼树,结果一定是“ 棵幼树成活”
B. 种植 棵幼树,结果一定是“ 棵幼树成活”和“ 棵幼树不成活”
C. 种植 棵幼树,恰好有“ 棵幼树不成活”
D. 种植 棵幼树,当 越来越大时,种植成活幼树的频率会越来越稳定于
7. 下列叙述随机事件的频率与概率的关系中,说法正确的是
A. 频率就是概率 B. 频率是随机的,与试验次数无关
C. 概率是稳定的,与试验次数无关 D. 概率是随机的,与试验次数有关
8. 在大量重复试验中,关于随机事件发生的频率与概率,下列说法正确的是
A. 频率就是概率
B. 频率与试验次数无关
C. 概率是随机的,与频率无关
D. 随着试验次数的增加,频率一般会越来越接近概率
9. 甲、乙两名同学在一次用频率去估计概率的试验中统计了某一结果出现的频率,绘出的统计图如图所示,则符合这一结果的试验可能是
A. 掷一枚正六面体的骰子,出现 点的概率
B. 从一个装有 个白球和 个红球的袋子中任取 球,取到红球的概率
C. 抛一枚硬币,出现正面的概率
D. 任意写一个整数,它能被 整除的概率
10. 如图,正方形 内有一个圆 .电脑可设计程序:在正方形内可随机产生一系列点,当点数很多时,电脑自动统计正方形内的点数 ,圆 内的点数 (在正方形边上和圆上的点不在统计中),利用频率估计概率的原理,可推得 的大小是
A. B. C. D.
二、填空题(共6小题)
11. 年北京冬奥会的吉祥物有两种:冰墩墩和雪容融.在一个不透明的袋子里放有 张吉祥物的卡片,每张卡片写有一种吉祥物的名称,小杰从中任意抽取一张再放回,重复试验 次后,摸到冰墩墩 次.则可估计袋子里写有“雪容融”的卡片数量是 .
12. 蒲丰是十八世纪的法国著名数学家,他发现:在一张白纸上画满距离相等的平行线,将长度为平行线间距离一半的小针随意投掷到纸面上,则小针与直线相交的概率就是圆周率 的倒数.
统计试验数据:共投针 次,其中小针与直线相交的次数有 次.由此可估计 的近似值为 (保留到小数点后第三位).
13. 在一个不透明的布袋中,有黄色、白色的乒乓球共10个,这些球除颜色外都相同.小刚通过多次摸球实验后发现其中摸到黄球的频率稳定在60%,则布袋中白色球的个数很可能是 个.
14. 一个暗箱中装有只有颜色不同的 ()个布娃娃,分别是 个白娃娃、 个绿娃娃, 个红娃娃和 个黄娃娃,从中任意拿出一个布娃娃,记下颜色后放回,经过大量重复试验,把拿出白娃娃,绿娃娃,红娃娃的频率绘制成如图所示的条形统计图(未绘制完整).根据题中给出的信息,暗箱中黄娃娃的个数为 .
15. 如图,在半径为 的 中,随意向圆内投掷一个小球,经过大量重复投掷后发现,小球落在阴影部分的频率稳定在 ,则 的长约为 .(结果保留 )
16. 某水果公司以 元/千克的成本价购进 苹果.公司想知道苹果的损坏率,从所有苹果中随机抽取若干进行统计,部分结果如表:
估计这批苹果损坏的概率为 (精确到 ),据此,若公司希望这批苹果能获得利润 元,则销售时(去掉损坏的苹果)售价应至少定为 元/千克.
三、解答题(共6小题)
17. 在一个不透明的盒子里装有只有颜色不同的黑、白两种球共 个,小明做摸球试验,他将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程,下表是试验中的一组统计数据:
(1)完成表格(除不尽的精确到 ).
(2)请估计当 很大时,摸到白球的频率将会接近 (精确到 ).
(3)试估算盒子里黑、白两种颜色的球各有多少只
18. 通过试验判断:掷一枚图钉,落到地面时,图钉的针尖可能朝上也可能朝下,“针尖朝上”与“针尖朝下”是不是等可能事件
找几个同学先分头进行掷图钉的试验,再合在一起统计试验结果,根据频率估计“针尖朝上”的概率与“针尖朝下”的概率.
19. 小明从一本书中随机抽取了 页,在累计 页至 页中的“的”字和“了”字出现的次数后,分别求出了它们出现的频率,并绘制了如下统计图(如图中页数 对应的频率是三页中累计的结果).
(1)随着统计页数的增加,这两个字出现的频率是如何变化的
(2)你认为该书中的“的”和“了”两个字出现的频率哪个高
20. 小明和小杰为了估计抛掷图钉时针尖朝上的概率,分别做了试验.小明的试验结果记录在表一,小杰的试验结果记录在表二.
表一:
表二:
(1)在小明的试验中,针尖朝上的频率是多少 在小杰的试验中,针尖朝上的频率又是多少
(2)求针尖朝上的概率估计值,并说明理由.
21. 如图 ,一枚扁式图钉由钉帽和钉尖两部分组成.通过试验发现,这枚图钉落在坚硬的地面上,顶尖可能朝下也可能朝上.
(1)请你与一位同伴合作,做抛掷扁式图钉的试验,并将两人的试验结果分别记录如下表(表 ,表 ).
表
表
(2)分别写出你和同伴在试验中钉尖朝上和朝下的频率.
(3)求钉尖朝上的概率估计值.
(4)近年来在中学校园中,更常见的是另一种图钉(如图 ),请从概率的角度解释更换为这种图钉的原因.
22. 新冠疫情期间,某校开展线上教学,有“录播”和“直播”两种教学方式供学生选择其一种.为分析该校学生线上学习情况,在接受这两种教学方式的学生中各随机抽取 人调查学习参与度,数据整理结果如下表(数据分组包含左端值不包含右端值).
(1)你认为哪种教学方式学生的参与度更高 简要说明理由.
(2)从教学方式为“直播”的学生中任意抽取一位学生,估计该学生的参与度在 及以上的概率是多少.
(3)该校共有 名学生,选择“录播”和“直播”的人数之比为 ,估计参与度在 以下的共有多少人.
答案
1. D
2. D
【解析】由题中的折线统计图可知,随着试验次数的增加,该结果出现的频率稳定在 附近,可估计该结果出现的概率为 .袋中装有大小和质地都相同的 个红球和 个黄球,从中随机取一个,取到红球的概率为 ,故A不符合题意;
掷一枚质地均匀的正六面体骰子,向上的面的点数是偶数的概率为 ,故B不符合题意;
先后两次掷一枚质地均匀的硬币,两次都反面朝上的概率为 ,故C不符合题意;
先后两次掷一枚质地均匀的正六面体骰子,两次向上的面的点数之和是 或超过 的概率为 ,故D符合题意.
3. D
【解析】题中 个图形中,中心对称图形有 个,非中心对称图形有 个,轴对称图形有 个,既是中心对称图形又是轴对称图形的有 个.
由题中频率折线统计图可知,该结果出现的频率逐渐稳定在 附近,可估计该结果出现的概率为 .
选项A,抽出的是中心对称图形的概率是 ,不符合题意;
选项B,抽出的是非中心对称图形的概率是 ,不符合题意;
选项C,抽出的是轴对称图形的概率是 ,不符合题意;
选项D,抽出的既是中心对称图形也是轴对称图形的概率是 ,符合题意,
故选D.
4. B
【解析】设盒子中黄球的个数为 ,
通过大量重复试验后发现,摸到黄球的频率稳定在 ,
估计任意摸出一个球,是黄球的概率为 .
根据题意,得 ,
解得 ,
即盒子中黄球的个数为 .
5. C
【解析】由表格可知,随着抽查车辆数逐渐增大,能礼让行人的车辆的频率趋近于 ,
可估计驾驶员能主动给行人让路的概率为 .
6. D
【解析】用频率估计的概率是在大量重复试验中得到的概率的近似值.可知A,B,C错误,D正确.故选D.
7. C
【解析】频率是随机的,随试验而变化,但概率是唯一确定的一个值,在大量重复试验中,随试验次数的增大,频率会逐渐稳定于概率附近.
8. D
【解析】【分析】根据大量重复试验事件发生的频率逐渐稳定到某个常数附近,可以用这个常数估计这个事件发生的概率解答.
【解析】解:大量重复试验事件发生的频率逐渐稳定到某个常数附近,可以用这个常数估计这个事件发生的概率,
选项说法正确.
故选:.
【点评】本题考查了利用频率估计概率的知识,大量重复试验事件发生的频率逐渐稳定到某个常数附近,可以用这个常数估计这个事件发生的概率.
9. B
10. B
【解析】设圆的半径为 ,则正方形的边长为 ,
根据题意得 ,
故 .
11. 张
12.
13. 4
【解析】【分析】设出黄球的个数,根据黄球的频率求出黄球的个数即可解答.
【解析】解:设黄球的个数为,
共有黄色、白色的乒乓球10个,黄球的频率稳定在60%,
≈0.6,
解得,,
布袋中白色球的个数很可能是个.
【点评】考查利用频率估计概率.大量反复试验下频率稳定值即概率.关键是根据黄球的频率得到相应的等量关系.
14.
【解析】由题中条形统计图可知,拿出绿娃娃的频率为 ,估计从中任意拿出一个布娃娃,恰好拿出的是绿娃娃的概率为 ,
,
解得 ,
经检验, 是原分式方程的解,
暗箱中黄娃娃的个数为 .
15.
【解析】 大量重复投掷后发现,小球落在阴影部分的频率稳定在 ,
扇形面积占圆面积的 ,
的长占圆周长的 ,
的长约为 .
16. ,
【解析】根据表中的损坏的频率,当实验次次数的增多时,苹果损坏的频率越来越稳定在 左右,所以苹果的损坏概率为 .
根据估计的概率可以知道,在 苹果中完好苹果的质量为 .
设每千克苹果的销售价为 元,
则应有 ,
解得 .
17. (1)
(2)
(3) ,
.
答:黑球有 个,白球有 个.
18. 略
19. (1) “的”字频率趋近 ,“了”字频率趋近 .
(2) “的”字出现的频率高.
20. (1) 小明的试验中针尖朝上的频率为 ,小杰的试验中针尖朝上的频率为 .
(2) 图钉针尖朝上的概率估计是 ,因为大数次试验的频率才稳定于概率附近.
21. (1) 填表(略);
(2) 过程略;
(3) 过程略,依据第()问的频率,但要注意选择大次数的试验进行计算;
(4) 图 的图钉落下后钉尖朝上的概率接近 ,安全性更高.
22. (1) “直播”教学方式学生的参与度更高.
理由:“直播”参与度在 以上的人数为 ,“录播”参与度在 以上的人数为 ,参与度在 以上的“直播”人数远多于“录播”人数,
所以“直播”教学方式学生的参与度更高.
(2) .
答:估计该学生的参与度在 及以上的概率是 .
(3) 选择“录播”的学生数为 ,选择“直播”的学生数为 ,
所以“录播”参与度在 以下的学生数为 ,“直播”参与度在 以下的学生数为 ,
所以估计参与度在 以下的学生共有 (人).
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
