【2013年最新同步教辅】高中数学(新课标人教版必修5 B版)配套精练检测题:第一章 解三角形(含答案解析)
文档属性
| 名称 | 【2013年最新同步教辅】高中数学(新课标人教版必修5 B版)配套精练检测题:第一章 解三角形(含答案解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 102.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-09-17 10:38:23 | ||
图片预览



文档简介
第一章 解三角形
一、选择题.
1. 在△ABC 中,b = 8,c =,S△ABC =,则∠A 等于( ).
A. 30 o B. 60o C. 30o 或 150o D. 60o 或120o
2. 在△ABC中,若a = 2b sin A,则∠B为( ).
A. B. C.或 D.或
3. △ABC中,下述表达式:①sin(A + B)+ sin C;②cos(B + C)+ cos A;
③,其中表示常数的是( ).
A. ①和② B. ①和③
C. ②和③ D. ①②③
4. 已知 a,b,c 是△ABC三边的长,若满足等式(a + b - c)(a + b + c)= ab,则∠C的大小为( ).
A. 60o B. 90o C. 120o D. 150o
5. 若△ABC满足下列条件:
① a = 4,b ( 10,(A ( 30(;
② a ( 6,b ( 10,(A ( 30(;
③ a ( 6,b ( 10,(A ( 150(;
④ a ( 12,b ( 10,(A ( 150(;
⑤ a + b + c = 4,(A ( 30(,(B ( 45(.
则△ABC恰有一个的是( ).
A. ①④ B. ①②③ C. ④⑤ D. ①②⑤
6. △ABC中,若 sin(A + B)sin(A - B)= sin2 C,则△ABC 是( ).
A. 锐角三角形 B. 直角三角形 C. 钝角三角形 D. 等腰三角形
7. 在△ABC中,若∠C = 60o,则cos A cos B的取值范围是( ).
A. B. C. D. 以上都不对
8. △ABC 中,若其面积 S =(a2 + b2 - c2),则∠C =( ).
A. B. C. D.
二、填空题.
1. 在△ABC 中,如果 sin A∶sin B∶sin C = 2∶3∶4,那么cos C等于 .
2. 若△ABC的三内角(A,(B,(C满足 sin A ( 2sin Ccos B,则△ABC为 三角形.
3. 若△ABC的三边长分别为4,5,7,则△ABC的面积 ( , 内切圆半径 ( .
4.若△ABC的三内角A,B,C成等差数列,则cos2 A + cos2 C的最小值为 .
5. 一船以每小时15 km的速度向东航行,船在A处看到一个灯塔B在北偏东处;行驶4 h后,船到达C处,看到这个灯塔在北偏东处. 这时船与灯塔的距离为 km.
6. 在△ABC中,已知 AB = l,∠C = 50°,当∠B = 时,BC的长取得最大值.
三、解答题.
1. 如图△ABC中,点D在边 BC上,且BD = 2,DC = 1,∠B = 60°,∠ADC = 150°,求AC的长及△ABC的面积.
2. 在△ABC中,A = 45°,B∶C = 4∶5,最大边长为10,求角B,C,△ABC外接圆半径R及面积S.
3. 在△ABC中,a,b,c分别为角 A,B,C的对边,且.
(1)求∠A的大小;
(2)若a =,b + c = 3,求b和c的值.
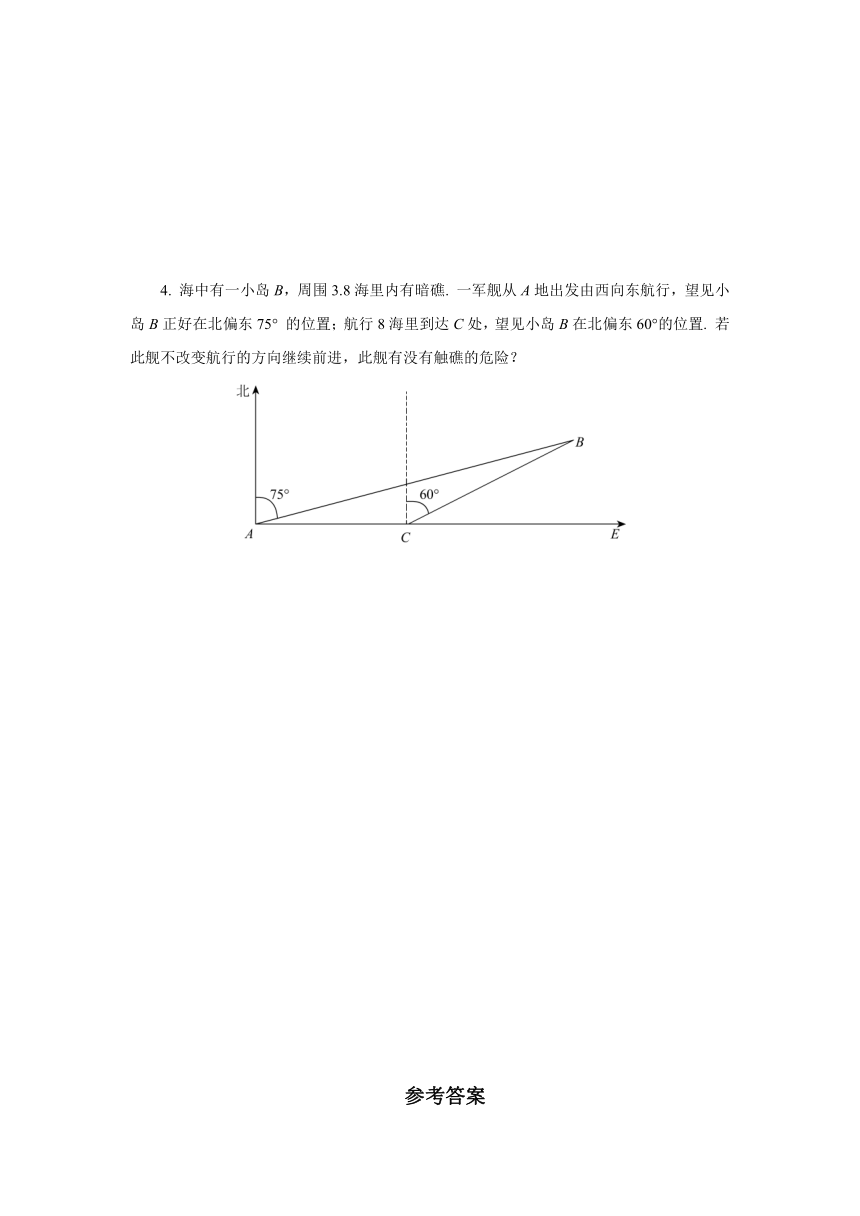
4. 海中有一小岛B,周围3.8海里内有暗礁. 一军舰从A地出发由西向东航行,望见小岛B正好在北偏东75° 的位置;航行8海里到达C处,望见小岛B在北偏东60°的位置. 若此舰不改变航行的方向继续前进,此舰有没有触礁的危险?
参考答案
一、选择题.
1. C
【解析】 bc sin A = 16,
∴ sin A =,
A = 30° ,或 150° .
2. D
【解析】 =,
∴ ,
∴ sin B =,∴ B =,或.
3. C
【解析】 ①sin(A + B)+ sin C = 2sin C,不一定为常数.
②cos(B + C)+ cos A = - cos A + cos A = 0,
③= tantan= cottan= 1.
∴ ②和③为常数.
4. C
【解析】 原式可化为 a2 + ab + b2 - c2 = 0,
∴ cos C == -,
∴ C=120°.
5. C
【解析】 ①∵ sin B = ==>1,
∴ △ABC不存在.
②∵ bsin A = 10×sin 30° = 5,且5<6<10,
∴ △ABC有两解.
③∵ ∠A = 150° 且a<b,
∴ △ABC不存在.
④∵ ∠A = 150° 且a>b,
∴ △ABC有一解.
⑤ 由已知,得∠C = 105°.
当 时,各边有正数解.
∴ △ABC有一解.
∴ ④⑤符合题条件.
6. B
【解析】 sin(A + B)sin(A - B)= sin2 C,
∴ sin C sin(A - B)= sin2 C.
∵ C∈(0,π),
∴ sin(A - B)= sin C = sin(A + B).
∴ sin A cos B - cos A sin B = sin A cos B+ cos A sin B,
∴ cos A sin B = 0,
∴ A =.
∴ △ABC为直角三角形.
7. A
【解析】 cos A cos B = cos(120o- B)cos B
=(-cos B +sin B)cos B
= -(1 + cos 2B)+sin 2B =sin(2B - 30o)-,
∵ B∈(0o,120o),
∴ -30°<2B - 30°<210°.
∴ 由图象知cos A cos B∈.
8. C
【解析】 由题知ab sin C =(a2 + b2 - c2),
∴ sin C == cos C,
∴ C =.
二、填空题.
1. -.
【解析】 因为sin A∶sin B∶sin C = a∶b∶c = 2∶3∶4,
所以设 a = 2k,b = 3k,c = 4k.
cos C === -.
2. 等腰.
【解析】 ∵ sin A = sin(B + C)= 2sin C cos B,
∴ sin B cos C + cos B sin C = 2 sin C cos B,
∴tan B = tan C,
∵ B,C∈(0,?),
∴ B = C.
即为等腰三角形.
3. 4;.
【解析】 ∵ cos ? == -,
∴ sin ? =.
∴ S =×4×5×= 4.
∵ ,
∴ .
4. .
【解析】 ∵ C + A = 2B,∴ B =.
设A =- x,C =+ x,则
cos2 A + cos2 C = cos2(- x)+ cos2(+ x)
=(cos x +sin x)2 +(cos x -sin x)2
=cos2 x+sin2 x =+ sin2 x≥.
5. .
【解析】 ,
BC =××60 = 30.
6. 40°.
【解析】 ,
∴ BC =≤,
∴ sin(50° + B)= 1时,BC最长,
此时 B?????°.
三、解答题.
1. 【解】在△ABD中,∠BAD = 150o- 60o= 90o,∴ AD = 2sin 60o =.
在△ACD中,AC2 =()2+12 - 2××1×cos 150o= 7,
∴ AC =.
∴ AB = 2cos 60° = 1,S△ABC =×1×3×sin 60°=.
2. 【解】由A + B + C = 180°,A = 45°,可得 B = 60°,C = 75°.
由正弦定理,R == 5(-).
由面积公式,S =bcsin A = c · 2Rsin Bsin A = 75-25.
3. (1)【解】由及A + B + C = 180°,
得2[1-cos(B + C)]-2cos2 A + 1 =,
∴ 4(1 + cosA)- 4cos2 A = 5,
即4 cos2 A- 4cos A + 1= 0,∴ cos A =,
∵ 0°<A<180°,
∴ A = 60°.
(2)【解】由余弦定理,得,
∵ cos A =,∴ =,
∴ (b + c)2 - a2 = 3bc.
将a =,b + c = 3代入上式,得bc = 2.
由 得 或
4.【解】如图,过点B作BD⊥AE且交AE于D.
由已知,AC = 8,∠ABD = 75o,∠CBD = 60o.
在Rt△ABD 中,AD = BD · tan∠ABD = BD · tan 75o.
在Rt△CBD 中,CD = BD · tan∠CBD = BD · tan 60o.
∴ AD - CD = BD(tan 75o- tan 60o)= AC = 8,
∴ BD == 4>3.8.
∴ 该军舰没有触礁的危险.
一、选择题.
1. 在△ABC 中,b = 8,c =,S△ABC =,则∠A 等于( ).
A. 30 o B. 60o C. 30o 或 150o D. 60o 或120o
2. 在△ABC中,若a = 2b sin A,则∠B为( ).
A. B. C.或 D.或
3. △ABC中,下述表达式:①sin(A + B)+ sin C;②cos(B + C)+ cos A;
③,其中表示常数的是( ).
A. ①和② B. ①和③
C. ②和③ D. ①②③
4. 已知 a,b,c 是△ABC三边的长,若满足等式(a + b - c)(a + b + c)= ab,则∠C的大小为( ).
A. 60o B. 90o C. 120o D. 150o
5. 若△ABC满足下列条件:
① a = 4,b ( 10,(A ( 30(;
② a ( 6,b ( 10,(A ( 30(;
③ a ( 6,b ( 10,(A ( 150(;
④ a ( 12,b ( 10,(A ( 150(;
⑤ a + b + c = 4,(A ( 30(,(B ( 45(.
则△ABC恰有一个的是( ).
A. ①④ B. ①②③ C. ④⑤ D. ①②⑤
6. △ABC中,若 sin(A + B)sin(A - B)= sin2 C,则△ABC 是( ).
A. 锐角三角形 B. 直角三角形 C. 钝角三角形 D. 等腰三角形
7. 在△ABC中,若∠C = 60o,则cos A cos B的取值范围是( ).
A. B. C. D. 以上都不对
8. △ABC 中,若其面积 S =(a2 + b2 - c2),则∠C =( ).
A. B. C. D.
二、填空题.
1. 在△ABC 中,如果 sin A∶sin B∶sin C = 2∶3∶4,那么cos C等于 .
2. 若△ABC的三内角(A,(B,(C满足 sin A ( 2sin Ccos B,则△ABC为 三角形.
3. 若△ABC的三边长分别为4,5,7,则△ABC的面积 ( , 内切圆半径 ( .
4.若△ABC的三内角A,B,C成等差数列,则cos2 A + cos2 C的最小值为 .
5. 一船以每小时15 km的速度向东航行,船在A处看到一个灯塔B在北偏东处;行驶4 h后,船到达C处,看到这个灯塔在北偏东处. 这时船与灯塔的距离为 km.
6. 在△ABC中,已知 AB = l,∠C = 50°,当∠B = 时,BC的长取得最大值.
三、解答题.
1. 如图△ABC中,点D在边 BC上,且BD = 2,DC = 1,∠B = 60°,∠ADC = 150°,求AC的长及△ABC的面积.
2. 在△ABC中,A = 45°,B∶C = 4∶5,最大边长为10,求角B,C,△ABC外接圆半径R及面积S.
3. 在△ABC中,a,b,c分别为角 A,B,C的对边,且.
(1)求∠A的大小;
(2)若a =,b + c = 3,求b和c的值.
4. 海中有一小岛B,周围3.8海里内有暗礁. 一军舰从A地出发由西向东航行,望见小岛B正好在北偏东75° 的位置;航行8海里到达C处,望见小岛B在北偏东60°的位置. 若此舰不改变航行的方向继续前进,此舰有没有触礁的危险?
参考答案
一、选择题.
1. C
【解析】 bc sin A = 16,
∴ sin A =,
A = 30° ,或 150° .
2. D
【解析】 =,
∴ ,
∴ sin B =,∴ B =,或.
3. C
【解析】 ①sin(A + B)+ sin C = 2sin C,不一定为常数.
②cos(B + C)+ cos A = - cos A + cos A = 0,
③= tantan= cottan= 1.
∴ ②和③为常数.
4. C
【解析】 原式可化为 a2 + ab + b2 - c2 = 0,
∴ cos C == -,
∴ C=120°.
5. C
【解析】 ①∵ sin B = ==>1,
∴ △ABC不存在.
②∵ bsin A = 10×sin 30° = 5,且5<6<10,
∴ △ABC有两解.
③∵ ∠A = 150° 且a<b,
∴ △ABC不存在.
④∵ ∠A = 150° 且a>b,
∴ △ABC有一解.
⑤ 由已知,得∠C = 105°.
当 时,各边有正数解.
∴ △ABC有一解.
∴ ④⑤符合题条件.
6. B
【解析】 sin(A + B)sin(A - B)= sin2 C,
∴ sin C sin(A - B)= sin2 C.
∵ C∈(0,π),
∴ sin(A - B)= sin C = sin(A + B).
∴ sin A cos B - cos A sin B = sin A cos B+ cos A sin B,
∴ cos A sin B = 0,
∴ A =.
∴ △ABC为直角三角形.
7. A
【解析】 cos A cos B = cos(120o- B)cos B
=(-cos B +sin B)cos B
= -(1 + cos 2B)+sin 2B =sin(2B - 30o)-,
∵ B∈(0o,120o),
∴ -30°<2B - 30°<210°.
∴ 由图象知cos A cos B∈.
8. C
【解析】 由题知ab sin C =(a2 + b2 - c2),
∴ sin C == cos C,
∴ C =.
二、填空题.
1. -.
【解析】 因为sin A∶sin B∶sin C = a∶b∶c = 2∶3∶4,
所以设 a = 2k,b = 3k,c = 4k.
cos C === -.
2. 等腰.
【解析】 ∵ sin A = sin(B + C)= 2sin C cos B,
∴ sin B cos C + cos B sin C = 2 sin C cos B,
∴tan B = tan C,
∵ B,C∈(0,?),
∴ B = C.
即为等腰三角形.
3. 4;.
【解析】 ∵ cos ? == -,
∴ sin ? =.
∴ S =×4×5×= 4.
∵ ,
∴ .
4. .
【解析】 ∵ C + A = 2B,∴ B =.
设A =- x,C =+ x,则
cos2 A + cos2 C = cos2(- x)+ cos2(+ x)
=(cos x +sin x)2 +(cos x -sin x)2
=cos2 x+sin2 x =+ sin2 x≥.
5. .
【解析】 ,
BC =××60 = 30.
6. 40°.
【解析】 ,
∴ BC =≤,
∴ sin(50° + B)= 1时,BC最长,
此时 B?????°.
三、解答题.
1. 【解】在△ABD中,∠BAD = 150o- 60o= 90o,∴ AD = 2sin 60o =.
在△ACD中,AC2 =()2+12 - 2××1×cos 150o= 7,
∴ AC =.
∴ AB = 2cos 60° = 1,S△ABC =×1×3×sin 60°=.
2. 【解】由A + B + C = 180°,A = 45°,可得 B = 60°,C = 75°.
由正弦定理,R == 5(-).
由面积公式,S =bcsin A = c · 2Rsin Bsin A = 75-25.
3. (1)【解】由及A + B + C = 180°,
得2[1-cos(B + C)]-2cos2 A + 1 =,
∴ 4(1 + cosA)- 4cos2 A = 5,
即4 cos2 A- 4cos A + 1= 0,∴ cos A =,
∵ 0°<A<180°,
∴ A = 60°.
(2)【解】由余弦定理,得,
∵ cos A =,∴ =,
∴ (b + c)2 - a2 = 3bc.
将a =,b + c = 3代入上式,得bc = 2.
由 得 或
4.【解】如图,过点B作BD⊥AE且交AE于D.
由已知,AC = 8,∠ABD = 75o,∠CBD = 60o.
在Rt△ABD 中,AD = BD · tan∠ABD = BD · tan 75o.
在Rt△CBD 中,CD = BD · tan∠CBD = BD · tan 60o.
∴ AD - CD = BD(tan 75o- tan 60o)= AC = 8,
∴ BD == 4>3.8.
∴ 该军舰没有触礁的危险.
