人教版数学八年级下册19.1.1变量与函数(2)教学设计
文档属性
| 名称 | 人教版数学八年级下册19.1.1变量与函数(2)教学设计 |

|
|
| 格式 | docx | ||
| 文件大小 | 281.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-22 16:09:12 | ||
图片预览




文档简介
19.1.1变量与函数(2)教学设计
一、 教材分析:
本节是人教版数学八年级下册第十九章第1节,在这一节中,学生首次接触函数这个概念,它是研究运动变化规律的重要数学模型,刻画了变化过程中变量之间的对应关系。函数概念是中学数学的核心概念,是之后学习各类函数、方程等内容的重要基础。因此,本节课具有极其重要的作用。
二、 学情分析:
八年级的学生求知欲旺盛,具有强烈的操作兴趣。观察能力、记忆能力和想象能力等也有了进一步的发展。但这一阶段自我意识增强,因此在教学中引导学生通过动手实践与探索,参与到函数概念的形成过程过程中去,激发他们的学习兴趣,并培养他们分析问题和解决问题的能力。同时向学生渗透变化与对应的思想和建模思想。
三、 教学目标:
1.知识与技能:
结合实例,了解函数的概念,了解自变量与函数的意义。能确定简单实际问题中函数自变量的取值范围,会求函数值。
过程与方法:
经历动手实践与探索,观察等活动参与函数概念的形成过程,初步体会变量之间的联系,感受变化与对应的思想,提高学生分析问题和解决问题的能力。
情感态度与价值观 :
在解决问题的过程中体会数学的应用价值,增强对学习的兴趣和积极参与数学活动的热情,感受数学的严谨性及数学结论的确定性。
四、教学重点:了解函数概念和自变量的意义。会求函数值。
教学难点:概括并理解函数概念中的单值对应关系。
五、 教学方法
启发式教学法、。分析归纳法、自主探究法、
六、教学准备
多媒体辅助教学。
七:教学过程
一:创设情境,提出问题:
提问:(1)同学们,上节课我们已经学习了常量与变量,那么我想问一下大家什么什么变量?什么什么常量?
(2)你能指出下列式子中的变量与常量吗?它们变量之间有什么关系吗?
y=2x a=3+2.4b C=2πR
学生独立思考并回答问题(1)小组合作讨论回答问题(2)
通过前面的问题,我们体会到万物皆变,在运动变化过程中往往蕴含着量的变化,这节课呢我们一起来研究两个变量之间的关系——函数。
(设计意图:通过复习上节课的内容,提出本节课需要研究的问题,引起合理的选择性注意,起先行组织者作用。)
二:合作探究,形成概念:
问题1:我们继续来看由71页问题所得的四个关系式
(1)s=60t;(2)y=10x;(3)S=πr ;(4)y=5-x
每个关系式中是否都存在两个变量?在这四个关系式中,是那一个量随那一个量的变化而变化?当一个变量取定一个值时?另一个变量的值是唯一确定的吗?
师生一起分析变化过程(1)中变量之间的关系,引导学生得出(1)有两个变量s,t,然后是s随着t的变化而变化。
设计意图:初步概括变量的联动性。
师生活动:教师引导学生取定t的一些值,计算s的对应值并列表。
T/h 1 2 3 4 5 ......
S/km 60 120 180 240 300 ......
在学生观察观察分析讨论发表自己意见的基础上,师生共同归纳:时间t,里程s的值是按照某种规律变化的。当t的值确定后,s 的值有一个且只有一个。也就是说,当t取定一个值时,s的值由t的值完全确定,而且唯一确定。
设计意图:通过师生,共同讨论,得出函数概念的第一次概括归纳的样例。
师生活动:引导学生对变化过程(2)-(4)进行类似于变化过程(1)的变量关系小组讨论分析之后得出:
上面的每个问题中的两个变量互相联系。当其中一个变量取定一个值时,另一个变量就有惟一确定的值与其对应。
设计意图:对能用解析式表示的变量之间的对应关系的共同特征进行初步概括。
问题2
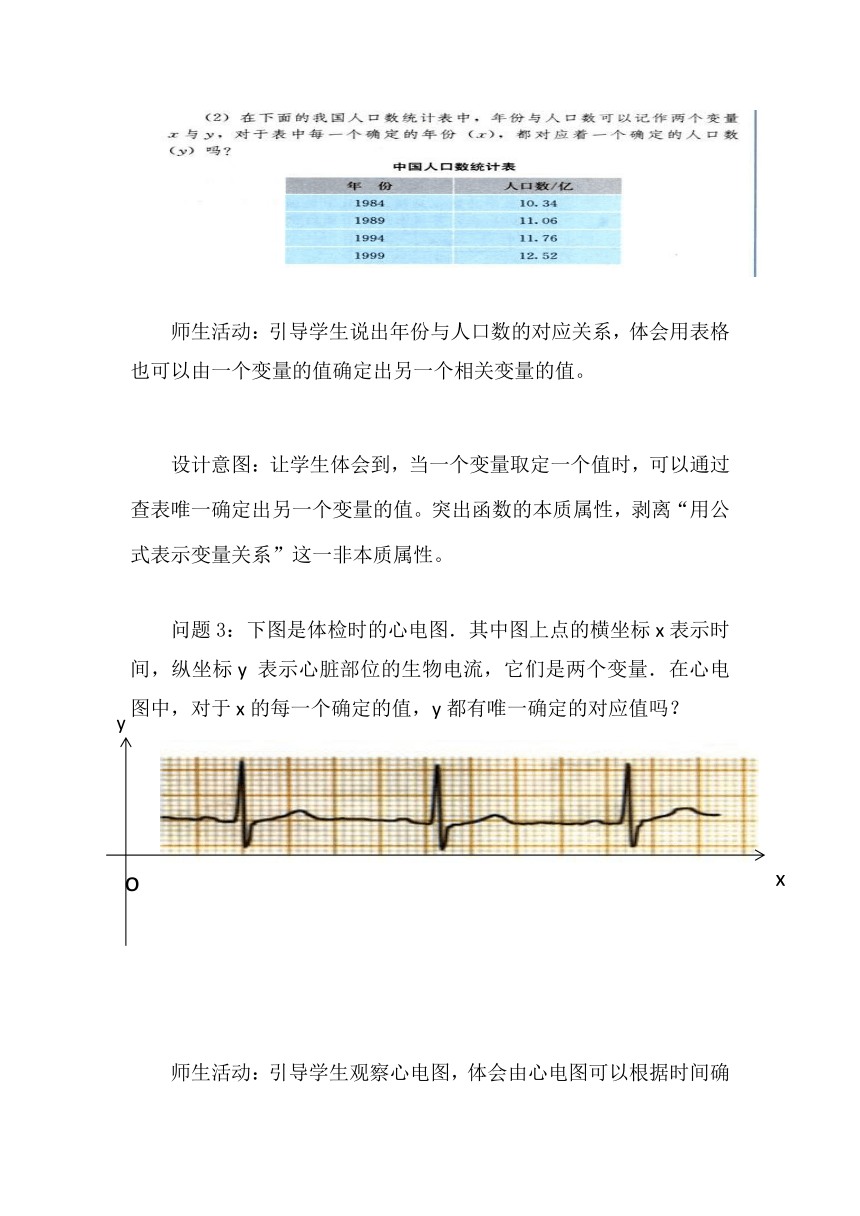
师生活动:引导学生说出年份与人口数的对应关系,体会用表格也可以由一个变量的值确定出另一个相关变量的值。
设计意图:让学生体会到,当一个变量取定一个值时,可以通过查表唯一确定出另一个变量的值。突出函数的本质属性,剥离“用公式表示变量关系”这一非本质属性。
问题3:下图是体检时的心电图.其中图上点的横坐标x表示时间,纵坐标y表示心脏部位的生物电流,它们是两个变量.在心电图中,对于x的每一个确定的值,y都有唯一确定的对应值吗?
师生活动:引导学生观察心电图,体会由心电图可以根据时间确定生物电流的数值。体会这也是变量之间的单值对应关系。
设计意图:让学生体会到,当一个变量取定一个值时,通过图像也可以确定另一个变量的唯一值。突出函数的本质属性。
问题4:上述实际问题中两个变量之间的关系,当一个变量取定一个值时,既有通过公式确定另一个变量唯一的值,又有通过对应表格确定另一个变量唯一的值,还有通过图像确定另一个变量唯一的值。综合这些现象,你能归纳出上面实例中变量之间关系的共同特点吗?请大家相互讨论。
学生分组讨论归纳出如下结论:
函数的概念:一般来说,在一个变化过程中,如果有两个变量x与y,并且对于x的每一个确定的值,y都有唯一确定的值与其对应,我们就说x是自变量,y是x的函数。
强调学生注意:一个变化过程中只有两个变量,两个变量之间的对应关系是“x的每一个确定的值y都有唯一确定的值与其对应”。“x的每一个确定的值”中的“确定”是指x的取值要符合变化过程的实际意义。
追问:请结合问题1(1)说说函数定义中“变化”“对应”“唯一确定”的含义。
师生活动:学生借助表格小组讨论
T/h 1 2 3 4 5 ......
S/km 60 120 180 240 300 ......
,
师引导点评并顺势带出函数值的概念:
如果当x=a时y=b,那么b叫做当自变量的值为a时的函数值。
可以认为问题(1)中,时间t是自变量,路程s是t的函数,当t=1时,函数值s=60,当t=2时,函数值s=120,
(设计意图:通过具体实例提出注意问题,帮助学生把握概念的本质特征,并在概念的形成过程中培养学生的观察、分析概括和抽象等能力。)
追问:(1)如何理解“对于x的每一个确定的值,y都有唯一确定的值与其对应”这句话?请举例说明。
(2)函数值由谁来确定?怎样求函数值?
(3)自变量和函数是相对而言的,它们二者之间有时可以互换。有时不能。
(4)思考问题3中,心脏部位的生物电流y是时间x的函数,但时间x不是生物电流y的函数。为什么
学生小组讨论师完善总结出:
变量x与y的关系可以是一对一,二对一,多对一。如果是一对多的情况就不是函数了。
确定函数值必须是首先确定两个变量之间的对应关系,然后确定自变量的值,根据对应关系确定函数值。
对函数概念的理解应抓住以下三点:
①某一变化过程中有两个变量
②一个变量的数值随着另一个变量的数值变化而变化
③自变量每确定一个值,函数就有一个并且只有一个值与之对应。
(设计意图:通过概括变量关系的共同特征,形成函数概念。)
练习1.写出下列各问题中的关系式,并指出其中的自变量与函数。
(1)正方形的面积S 随边长 x 的变化
(2)秀水村的耕地面积是106m2,这个村人均耕地面积y随着
人数x的变化而变化
长方形的周长是18 ,它的长是m,宽是n ;
师生活动:小组讨论得出结果并派代表回答。
(设计意图:通过练习,进一步帮助学生把握并理解概念的本质特征。)
三:初步练习,了解概念:
例1汽车油箱中有汽油50L,如果不再加油,那么油箱中的油量y(单位:L)随行驶路x(单位:km)的增加而减少,平均耗油量为0.1L/km.
师引导学生共同分析:
(1)写出表示y 与 x的函数关系的式子:
y= x=0
y= x=1
y= x=2
y= x=3
…… ……
y= x=x
(2)指出自变量x的取值范围:
最近:路程不能为负数,但可以取到0km,表示还没开始走,
最远:一共有50L油,耗油量为0.1L/km,有一个0.1L,跑1km,有两个0.1L,跑2km,要看50L里有多少个0.1L,就可以跑多少km,所以,50÷0.1=____km,最远可以跑________km.
∴_______≤x≤______
(3)汽车行驶200km时,油箱中还有多少汽油?
分析:
y=50-0.1x
相当于求x=200时,y的函数值。
最后师生共同归纳,得出结论,在这里进一步强调确定自变量的取值范围时,不仅要考虑到函数关系式必须有意义,而且还要注意问题的实际意义。
解::(1)行驶路程x是自变量,油箱中的油量y是x的函数,它们的关系为: y = 50-0.1x
仅从式子y = 50-0.1x看,x可以取任意实数。但是考虑到x代表的实际意义为行驶路程,因此x不能取负数,行驶中的耗油量为0.1x,它不能超过油箱中现有汽油量50,即
由x≥0及50≥0.1x 得 0 ≤ x ≤ 500
因此,自变量x的取值范围是
0 ≤ x ≤ 500
(3)当 x = 200时,函数 y 的值为:y=50-0.1×200=30
因此,当汽车行驶200 km时,油箱中还有油30L
总结:像y=50-0.1x这样,用关于自变量的数学式子表示函数与自变量之间的关系,是描述函数的常用方法,这种式子叫函数的解析式。
(设计意图:形成函数概念后,及时进行概念理解与巩固。)
练习:试写出函数解析式:
(1)改变正方形的边长x,正方形的面积S 随之改变。
(2)秀水村的耕地面积是106m2,这个村人均耕地面积y随着这个村
人数x的变化而变化
(3)每分向一水池注水0.1m3 ,注水量y随注水时间x的变化而变化。
(4)水池中有水10L,此后,每小时漏水0.05L,水池中的水量V随时间t的变化而变化。
(5)楼梯的上底长2cm。高3cm,下底长xcm大于上底但不超过5cm,写出梯形面积S关于x的函数解析式及自变量x的取值范围。
四:综合应用,深化理解:
1.下列关系中,y不是x函数的是( )
2.下列各曲线中那些表示y是x的函数:
3.4.下列各式中,X是自变量,请判断Y是不是X的函数?若是,求出自变量X的取值范围。
(1).y= 3x-5 ( 2).y= (3).y= +4. (4)y=
5. (1)在上面问题中所出现的各个函数中,自变量的取值有限制吗?如果有,写出它的取值范围.求出下列函数中自变量的取值范围
师生活动:学生独立完成后小组讨论,师个别指导,并派代表黑板板书练习4,5。师纠正书写格式。
设计意图:通过练习进一步理解函数的概念,让学生充分体会到许多问题中的变量关系都存在着函数关系。
五:课堂小结:
我感触最深(最困惑)的是……本节课——
整体的感知
我学会了……
我经历了……
(设计意图:以提问的方式请同学们说出自己的收获、成功的地方、困难的地方、疑问等。通过总结与归纳,完善学生已有的知识结构。)
六:作业布置:
复习本节课所学内容,预习下节课的内容。
课本81页复习巩固:第一题,第二题。
(设计意图:通过作业分层,做到面向全体学生,注重个体差异,使不同的学生各得其所。)
七:板书设计:
19.1.1变量与函数(2)
函数的概念:
一般来说,在一个变化过程中,如果有两个变量x与y,并且对于x的每一个确定的值,y都有唯一确定的值与其对应,我们就说x是自变量,y是x的函数。
函数值:
如果当x=a时y=b,那么b叫做当自变量的值为a时的函数值。
函数的解析式:
用关于自变量的数学式子表示函数与自变量之间的关系,是描述函数的常用方法,这种式子叫函数的解析式。
一、 教材分析:
本节是人教版数学八年级下册第十九章第1节,在这一节中,学生首次接触函数这个概念,它是研究运动变化规律的重要数学模型,刻画了变化过程中变量之间的对应关系。函数概念是中学数学的核心概念,是之后学习各类函数、方程等内容的重要基础。因此,本节课具有极其重要的作用。
二、 学情分析:
八年级的学生求知欲旺盛,具有强烈的操作兴趣。观察能力、记忆能力和想象能力等也有了进一步的发展。但这一阶段自我意识增强,因此在教学中引导学生通过动手实践与探索,参与到函数概念的形成过程过程中去,激发他们的学习兴趣,并培养他们分析问题和解决问题的能力。同时向学生渗透变化与对应的思想和建模思想。
三、 教学目标:
1.知识与技能:
结合实例,了解函数的概念,了解自变量与函数的意义。能确定简单实际问题中函数自变量的取值范围,会求函数值。
过程与方法:
经历动手实践与探索,观察等活动参与函数概念的形成过程,初步体会变量之间的联系,感受变化与对应的思想,提高学生分析问题和解决问题的能力。
情感态度与价值观 :
在解决问题的过程中体会数学的应用价值,增强对学习的兴趣和积极参与数学活动的热情,感受数学的严谨性及数学结论的确定性。
四、教学重点:了解函数概念和自变量的意义。会求函数值。
教学难点:概括并理解函数概念中的单值对应关系。
五、 教学方法
启发式教学法、。分析归纳法、自主探究法、
六、教学准备
多媒体辅助教学。
七:教学过程
一:创设情境,提出问题:
提问:(1)同学们,上节课我们已经学习了常量与变量,那么我想问一下大家什么什么变量?什么什么常量?
(2)你能指出下列式子中的变量与常量吗?它们变量之间有什么关系吗?
y=2x a=3+2.4b C=2πR
学生独立思考并回答问题(1)小组合作讨论回答问题(2)
通过前面的问题,我们体会到万物皆变,在运动变化过程中往往蕴含着量的变化,这节课呢我们一起来研究两个变量之间的关系——函数。
(设计意图:通过复习上节课的内容,提出本节课需要研究的问题,引起合理的选择性注意,起先行组织者作用。)
二:合作探究,形成概念:
问题1:我们继续来看由71页问题所得的四个关系式
(1)s=60t;(2)y=10x;(3)S=πr ;(4)y=5-x
每个关系式中是否都存在两个变量?在这四个关系式中,是那一个量随那一个量的变化而变化?当一个变量取定一个值时?另一个变量的值是唯一确定的吗?
师生一起分析变化过程(1)中变量之间的关系,引导学生得出(1)有两个变量s,t,然后是s随着t的变化而变化。
设计意图:初步概括变量的联动性。
师生活动:教师引导学生取定t的一些值,计算s的对应值并列表。
T/h 1 2 3 4 5 ......
S/km 60 120 180 240 300 ......
在学生观察观察分析讨论发表自己意见的基础上,师生共同归纳:时间t,里程s的值是按照某种规律变化的。当t的值确定后,s 的值有一个且只有一个。也就是说,当t取定一个值时,s的值由t的值完全确定,而且唯一确定。
设计意图:通过师生,共同讨论,得出函数概念的第一次概括归纳的样例。
师生活动:引导学生对变化过程(2)-(4)进行类似于变化过程(1)的变量关系小组讨论分析之后得出:
上面的每个问题中的两个变量互相联系。当其中一个变量取定一个值时,另一个变量就有惟一确定的值与其对应。
设计意图:对能用解析式表示的变量之间的对应关系的共同特征进行初步概括。
问题2
师生活动:引导学生说出年份与人口数的对应关系,体会用表格也可以由一个变量的值确定出另一个相关变量的值。
设计意图:让学生体会到,当一个变量取定一个值时,可以通过查表唯一确定出另一个变量的值。突出函数的本质属性,剥离“用公式表示变量关系”这一非本质属性。
问题3:下图是体检时的心电图.其中图上点的横坐标x表示时间,纵坐标y表示心脏部位的生物电流,它们是两个变量.在心电图中,对于x的每一个确定的值,y都有唯一确定的对应值吗?
师生活动:引导学生观察心电图,体会由心电图可以根据时间确定生物电流的数值。体会这也是变量之间的单值对应关系。
设计意图:让学生体会到,当一个变量取定一个值时,通过图像也可以确定另一个变量的唯一值。突出函数的本质属性。
问题4:上述实际问题中两个变量之间的关系,当一个变量取定一个值时,既有通过公式确定另一个变量唯一的值,又有通过对应表格确定另一个变量唯一的值,还有通过图像确定另一个变量唯一的值。综合这些现象,你能归纳出上面实例中变量之间关系的共同特点吗?请大家相互讨论。
学生分组讨论归纳出如下结论:
函数的概念:一般来说,在一个变化过程中,如果有两个变量x与y,并且对于x的每一个确定的值,y都有唯一确定的值与其对应,我们就说x是自变量,y是x的函数。
强调学生注意:一个变化过程中只有两个变量,两个变量之间的对应关系是“x的每一个确定的值y都有唯一确定的值与其对应”。“x的每一个确定的值”中的“确定”是指x的取值要符合变化过程的实际意义。
追问:请结合问题1(1)说说函数定义中“变化”“对应”“唯一确定”的含义。
师生活动:学生借助表格小组讨论
T/h 1 2 3 4 5 ......
S/km 60 120 180 240 300 ......
,
师引导点评并顺势带出函数值的概念:
如果当x=a时y=b,那么b叫做当自变量的值为a时的函数值。
可以认为问题(1)中,时间t是自变量,路程s是t的函数,当t=1时,函数值s=60,当t=2时,函数值s=120,
(设计意图:通过具体实例提出注意问题,帮助学生把握概念的本质特征,并在概念的形成过程中培养学生的观察、分析概括和抽象等能力。)
追问:(1)如何理解“对于x的每一个确定的值,y都有唯一确定的值与其对应”这句话?请举例说明。
(2)函数值由谁来确定?怎样求函数值?
(3)自变量和函数是相对而言的,它们二者之间有时可以互换。有时不能。
(4)思考问题3中,心脏部位的生物电流y是时间x的函数,但时间x不是生物电流y的函数。为什么
学生小组讨论师完善总结出:
变量x与y的关系可以是一对一,二对一,多对一。如果是一对多的情况就不是函数了。
确定函数值必须是首先确定两个变量之间的对应关系,然后确定自变量的值,根据对应关系确定函数值。
对函数概念的理解应抓住以下三点:
①某一变化过程中有两个变量
②一个变量的数值随着另一个变量的数值变化而变化
③自变量每确定一个值,函数就有一个并且只有一个值与之对应。
(设计意图:通过概括变量关系的共同特征,形成函数概念。)
练习1.写出下列各问题中的关系式,并指出其中的自变量与函数。
(1)正方形的面积S 随边长 x 的变化
(2)秀水村的耕地面积是106m2,这个村人均耕地面积y随着
人数x的变化而变化
长方形的周长是18 ,它的长是m,宽是n ;
师生活动:小组讨论得出结果并派代表回答。
(设计意图:通过练习,进一步帮助学生把握并理解概念的本质特征。)
三:初步练习,了解概念:
例1汽车油箱中有汽油50L,如果不再加油,那么油箱中的油量y(单位:L)随行驶路x(单位:km)的增加而减少,平均耗油量为0.1L/km.
师引导学生共同分析:
(1)写出表示y 与 x的函数关系的式子:
y= x=0
y= x=1
y= x=2
y= x=3
…… ……
y= x=x
(2)指出自变量x的取值范围:
最近:路程不能为负数,但可以取到0km,表示还没开始走,
最远:一共有50L油,耗油量为0.1L/km,有一个0.1L,跑1km,有两个0.1L,跑2km,要看50L里有多少个0.1L,就可以跑多少km,所以,50÷0.1=____km,最远可以跑________km.
∴_______≤x≤______
(3)汽车行驶200km时,油箱中还有多少汽油?
分析:
y=50-0.1x
相当于求x=200时,y的函数值。
最后师生共同归纳,得出结论,在这里进一步强调确定自变量的取值范围时,不仅要考虑到函数关系式必须有意义,而且还要注意问题的实际意义。
解::(1)行驶路程x是自变量,油箱中的油量y是x的函数,它们的关系为: y = 50-0.1x
仅从式子y = 50-0.1x看,x可以取任意实数。但是考虑到x代表的实际意义为行驶路程,因此x不能取负数,行驶中的耗油量为0.1x,它不能超过油箱中现有汽油量50,即
由x≥0及50≥0.1x 得 0 ≤ x ≤ 500
因此,自变量x的取值范围是
0 ≤ x ≤ 500
(3)当 x = 200时,函数 y 的值为:y=50-0.1×200=30
因此,当汽车行驶200 km时,油箱中还有油30L
总结:像y=50-0.1x这样,用关于自变量的数学式子表示函数与自变量之间的关系,是描述函数的常用方法,这种式子叫函数的解析式。
(设计意图:形成函数概念后,及时进行概念理解与巩固。)
练习:试写出函数解析式:
(1)改变正方形的边长x,正方形的面积S 随之改变。
(2)秀水村的耕地面积是106m2,这个村人均耕地面积y随着这个村
人数x的变化而变化
(3)每分向一水池注水0.1m3 ,注水量y随注水时间x的变化而变化。
(4)水池中有水10L,此后,每小时漏水0.05L,水池中的水量V随时间t的变化而变化。
(5)楼梯的上底长2cm。高3cm,下底长xcm大于上底但不超过5cm,写出梯形面积S关于x的函数解析式及自变量x的取值范围。
四:综合应用,深化理解:
1.下列关系中,y不是x函数的是( )
2.下列各曲线中那些表示y是x的函数:
3.4.下列各式中,X是自变量,请判断Y是不是X的函数?若是,求出自变量X的取值范围。
(1).y= 3x-5 ( 2).y= (3).y= +4. (4)y=
5. (1)在上面问题中所出现的各个函数中,自变量的取值有限制吗?如果有,写出它的取值范围.求出下列函数中自变量的取值范围
师生活动:学生独立完成后小组讨论,师个别指导,并派代表黑板板书练习4,5。师纠正书写格式。
设计意图:通过练习进一步理解函数的概念,让学生充分体会到许多问题中的变量关系都存在着函数关系。
五:课堂小结:
我感触最深(最困惑)的是……本节课——
整体的感知
我学会了……
我经历了……
(设计意图:以提问的方式请同学们说出自己的收获、成功的地方、困难的地方、疑问等。通过总结与归纳,完善学生已有的知识结构。)
六:作业布置:
复习本节课所学内容,预习下节课的内容。
课本81页复习巩固:第一题,第二题。
(设计意图:通过作业分层,做到面向全体学生,注重个体差异,使不同的学生各得其所。)
七:板书设计:
19.1.1变量与函数(2)
函数的概念:
一般来说,在一个变化过程中,如果有两个变量x与y,并且对于x的每一个确定的值,y都有唯一确定的值与其对应,我们就说x是自变量,y是x的函数。
函数值:
如果当x=a时y=b,那么b叫做当自变量的值为a时的函数值。
函数的解析式:
用关于自变量的数学式子表示函数与自变量之间的关系,是描述函数的常用方法,这种式子叫函数的解析式。
