数学人教A版(2019)选择性必修第一册1.1.1 空间向量及其线性运算 课件(共28张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第一册1.1.1 空间向量及其线性运算 课件(共28张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-21 00:00:00 | ||
图片预览







文档简介
(共28张PPT)
第一章 空间向量与立体几何
1.1.1 空间向量及其线性运算
问题1:
根据简介,你认为我们研究空间向量基本方法是什么
追问:
类比平面向量,你认为本章我们需要研究空间向量哪些内容
概念——运算——基本定理——坐标表示——应用
学习目标
1.通过类比平面向量理解空间向量的概念.
2.类比平面向量掌握一些特殊向量如零向量和单位向量,相等向量和相反向量,后续进一步理解共面向量.
3.类比平面向量线性运算掌握空间向量的加法、减法和数乘等线性法则、以及结合律和交换律等运算律,并通过空间几何体加深对运算的理解,培养数形结合思想,发展数学抽象等核心素养。
我们一起回忆一下平面向量的相关概念,类比的得出空间向量的概念
探究一:我们已经学面向量的概念,我们能否根据平面向量的概念类比得出空间向量的概念?
追问1:通过概念的学习,你认为空间向量对比平面向量差异是什么?
维度
追问2:从空间向量相等出发,你认为共线向量,有什么样的位置关系?如果在空间中任给两个向量,他们有什么样的位置关系?为什么?
空间中任意两个向量都可以平移到同一平面内
探究二:我们学面向量相关的概念后,学面向量的线性运算,通过解决追问2,你认为空间中任意两向量如何进行线性运算?
我们一起回忆一下平面向量的线性运算,类比的得出空间向量线性运算
合作探究
问题5 请大家以小组形式进行讨论
1.回忆出平面向量的加减法运算及其运算法则,还有平面向量的运算律有哪些?
2.空间向量的加减法及其法则,运算与平面向量是否一致?
问题4 平面向量的线性运算有哪些?我们当时是如何探究这些运算?
加法,减法,数乘
定义
法则
运算律
比一比,看哪个小组列出又快又准!
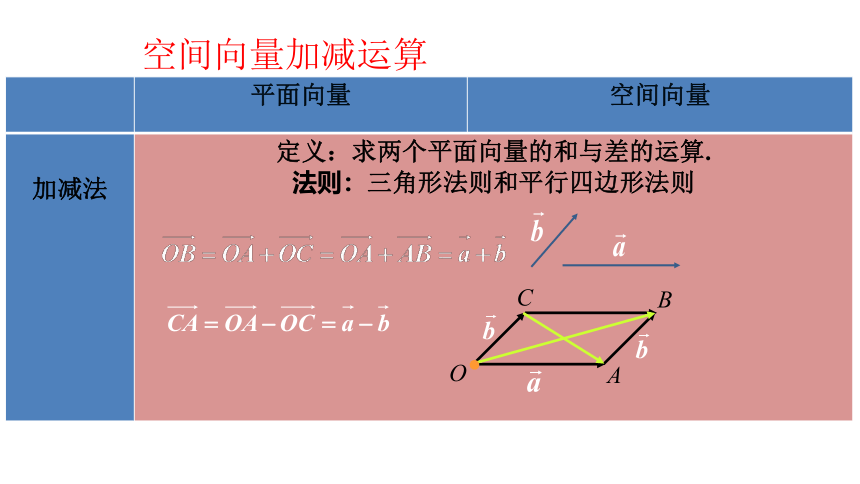
平面向量 空间向量
加减法 定义:求两个平面向量的和与差的运算. 法则:三角形法则和平行四边形法则
A
B
C
O
空间向量加减运算
平面向量 空间向量
数乘运算
空间向量数乘
平面向量 空间向量
运算法则
交换律:
结合律
分配律
由于任意两个空间向量都可以通过平移转化为同一平面内的向量,任意两个空间向量的运算就可以转化为平面向量的运算.
空间向量运算律
问题6 请大家思考下,下面的结合律是该如何解释?
A
B
C
D
A1
B1
C1
D1
体对角线
运算律的证明
问题7.我们知道,可以通过向量运算研究向量位置关系,那么对于空间向量位置关系你能找到哪些关系?得出哪些结论?
两个向量:共线,共面。
三个向量:共线,共面,不共面。
问题8 平面中两个共线向量的充要条件是什么?
直线的方向向量
空间向量同样适用
研究三:两向量共线
核心:直线可由直线上任意一点和他的方向向量确定。
1.共面向量:平行于同一平面的向量,叫做共面向量.
O
A
向量可以进行平移
平行即共面
研究四:共面向量
追问:空间中三个向量如何才能共面?
结合前面的研究方法,我们该从哪个方向去思考?
问题9 平面向量基本定理是什么?
平面向量基本定理:如果两个向量不共线,则向量与向量共面的充要条件是存在唯一的有序实数对(x,y)使.
向量可以进行平移
平面向量基本定理也可以是共面向量定理
注意:
(1)向量可以进行平移的
(2)空间任意两个向量是共面的,但空间任意三个向 量就不一定共面的了。
(3)判断三个向量是否共面
向量共面的充要条件:如果两个向量不共线,则向量与向量共面的充要条件是存在唯一的有序实数对(x,y)使.
向量共面
(4)判断点共面
例1 如图,已知平行四边形ABCD,从平面AC外一点O作射线OA,OB,OC,OD,在四条射线上分别取点E,F,G,H,使
求证:E,F,G,H四点共面
证明:
·
追问:最终的结果你还有没有其他的表示方法?能得到什么结论?
问题8 A,B,P三点共线的充要条件是什么?
问题9 P与A,B,C四点共面的充要条件是什么?
你能不能给出证明?
类比
四点共面结论
【做一做】已知O为空间任意一点,若,则四点P,A,B,C( )
A.一定不共面 B.一定共面 C.不一定共面 D.无法判断
【答案】B
2.空间的四点M、A、B、C四点共面,只需满足,且.
1.空间的三点M、A、B三点共线,只需满足,
且。
【重要结论】
典例
典型例题
2.空间向量的线性运算
例2. 如图所示,在平行六面体ABCD A1B1C1D1中,设=a,=b,=c,M,N,P分别是AA1,BC,C1D1的中点,试用a,b,c表示以下各向量:
(1);(2);(3)+.
[解析] (1)因为P是C1D1的中点,所以=++=a++=a+c+=a+c+b.
(2)因为N是BC的中点,所以=++=-a+b+=-a+b+=-a+b+c.
(3)因为M是AA1的中点,所以=+=+
-a+(a+b+c)=a+b+c,
又=+=+=+=c+a,
所以+=(a+b+c)+(c+a)=a+b+c.
向量的加法运算!
典型例题
3.空间向量共线问题
例3.如图,在正方体ABCD-A1B1C1D1中,E在A1D1上,且,F在对角线A1C上,且,
求证:E,F,B三点共线.
【解析】设a,=b,=c,
∵,,∴,,而==b
∴=b,==.
∴,又,
∴=,即E,F,B三点共线.
典型例题
【巩固练习4】在下列条件中,使M与A、B、C一定共面的是( )
A.B.
C.D.
【解析】空间的四点M、A、B、C四点共面,只需满足,且即可,对于A,中0,故此时四点M、A、B、C四点不共面;
对于B,中,此时四点M、A、B、C四点不共面;
对于C,,,即,此时四点M、A、B、C四点共面;
对于D,,则,此时,四点M、A、B、C四点不共面;故选:C
操作演练 素养提升
1.如图,在四棱柱的上底面中,,则下列向量相等的是( )
A.与 B.与 C.与 D.与
2.如图,直三棱柱ABC-A1B1C1中,若,,,则等于( )
A. B. C. D.
3.设空间任意一点O和不共线三点A,B,C,且点P满足向量关系,
若P,A,B,C四点共面,则______.
4.如图,已知四边形ABCD是空间四边形,E,H分别是边AB,AD的中点,F,G分别是边CB,CD上的点,且,.求证:四边形EFGH是梯形.
答案:1.D 2.C 3.1 4.略
课堂小结
知识总结
第一章 空间向量与立体几何
1.1.1 空间向量及其线性运算
问题1:
根据简介,你认为我们研究空间向量基本方法是什么
追问:
类比平面向量,你认为本章我们需要研究空间向量哪些内容
概念——运算——基本定理——坐标表示——应用
学习目标
1.通过类比平面向量理解空间向量的概念.
2.类比平面向量掌握一些特殊向量如零向量和单位向量,相等向量和相反向量,后续进一步理解共面向量.
3.类比平面向量线性运算掌握空间向量的加法、减法和数乘等线性法则、以及结合律和交换律等运算律,并通过空间几何体加深对运算的理解,培养数形结合思想,发展数学抽象等核心素养。
我们一起回忆一下平面向量的相关概念,类比的得出空间向量的概念
探究一:我们已经学面向量的概念,我们能否根据平面向量的概念类比得出空间向量的概念?
追问1:通过概念的学习,你认为空间向量对比平面向量差异是什么?
维度
追问2:从空间向量相等出发,你认为共线向量,有什么样的位置关系?如果在空间中任给两个向量,他们有什么样的位置关系?为什么?
空间中任意两个向量都可以平移到同一平面内
探究二:我们学面向量相关的概念后,学面向量的线性运算,通过解决追问2,你认为空间中任意两向量如何进行线性运算?
我们一起回忆一下平面向量的线性运算,类比的得出空间向量线性运算
合作探究
问题5 请大家以小组形式进行讨论
1.回忆出平面向量的加减法运算及其运算法则,还有平面向量的运算律有哪些?
2.空间向量的加减法及其法则,运算与平面向量是否一致?
问题4 平面向量的线性运算有哪些?我们当时是如何探究这些运算?
加法,减法,数乘
定义
法则
运算律
比一比,看哪个小组列出又快又准!
平面向量 空间向量
加减法 定义:求两个平面向量的和与差的运算. 法则:三角形法则和平行四边形法则
A
B
C
O
空间向量加减运算
平面向量 空间向量
数乘运算
空间向量数乘
平面向量 空间向量
运算法则
交换律:
结合律
分配律
由于任意两个空间向量都可以通过平移转化为同一平面内的向量,任意两个空间向量的运算就可以转化为平面向量的运算.
空间向量运算律
问题6 请大家思考下,下面的结合律是该如何解释?
A
B
C
D
A1
B1
C1
D1
体对角线
运算律的证明
问题7.我们知道,可以通过向量运算研究向量位置关系,那么对于空间向量位置关系你能找到哪些关系?得出哪些结论?
两个向量:共线,共面。
三个向量:共线,共面,不共面。
问题8 平面中两个共线向量的充要条件是什么?
直线的方向向量
空间向量同样适用
研究三:两向量共线
核心:直线可由直线上任意一点和他的方向向量确定。
1.共面向量:平行于同一平面的向量,叫做共面向量.
O
A
向量可以进行平移
平行即共面
研究四:共面向量
追问:空间中三个向量如何才能共面?
结合前面的研究方法,我们该从哪个方向去思考?
问题9 平面向量基本定理是什么?
平面向量基本定理:如果两个向量不共线,则向量与向量共面的充要条件是存在唯一的有序实数对(x,y)使.
向量可以进行平移
平面向量基本定理也可以是共面向量定理
注意:
(1)向量可以进行平移的
(2)空间任意两个向量是共面的,但空间任意三个向 量就不一定共面的了。
(3)判断三个向量是否共面
向量共面的充要条件:如果两个向量不共线,则向量与向量共面的充要条件是存在唯一的有序实数对(x,y)使.
向量共面
(4)判断点共面
例1 如图,已知平行四边形ABCD,从平面AC外一点O作射线OA,OB,OC,OD,在四条射线上分别取点E,F,G,H,使
求证:E,F,G,H四点共面
证明:
·
追问:最终的结果你还有没有其他的表示方法?能得到什么结论?
问题8 A,B,P三点共线的充要条件是什么?
问题9 P与A,B,C四点共面的充要条件是什么?
你能不能给出证明?
类比
四点共面结论
【做一做】已知O为空间任意一点,若,则四点P,A,B,C( )
A.一定不共面 B.一定共面 C.不一定共面 D.无法判断
【答案】B
2.空间的四点M、A、B、C四点共面,只需满足,且.
1.空间的三点M、A、B三点共线,只需满足,
且。
【重要结论】
典例
典型例题
2.空间向量的线性运算
例2. 如图所示,在平行六面体ABCD A1B1C1D1中,设=a,=b,=c,M,N,P分别是AA1,BC,C1D1的中点,试用a,b,c表示以下各向量:
(1);(2);(3)+.
[解析] (1)因为P是C1D1的中点,所以=++=a++=a+c+=a+c+b.
(2)因为N是BC的中点,所以=++=-a+b+=-a+b+=-a+b+c.
(3)因为M是AA1的中点,所以=+=+
-a+(a+b+c)=a+b+c,
又=+=+=+=c+a,
所以+=(a+b+c)+(c+a)=a+b+c.
向量的加法运算!
典型例题
3.空间向量共线问题
例3.如图,在正方体ABCD-A1B1C1D1中,E在A1D1上,且,F在对角线A1C上,且,
求证:E,F,B三点共线.
【解析】设a,=b,=c,
∵,,∴,,而==b
∴=b,==.
∴,又,
∴=,即E,F,B三点共线.
典型例题
【巩固练习4】在下列条件中,使M与A、B、C一定共面的是( )
A.B.
C.D.
【解析】空间的四点M、A、B、C四点共面,只需满足,且即可,对于A,中0,故此时四点M、A、B、C四点不共面;
对于B,中,此时四点M、A、B、C四点不共面;
对于C,,,即,此时四点M、A、B、C四点共面;
对于D,,则,此时,四点M、A、B、C四点不共面;故选:C
操作演练 素养提升
1.如图,在四棱柱的上底面中,,则下列向量相等的是( )
A.与 B.与 C.与 D.与
2.如图,直三棱柱ABC-A1B1C1中,若,,,则等于( )
A. B. C. D.
3.设空间任意一点O和不共线三点A,B,C,且点P满足向量关系,
若P,A,B,C四点共面,则______.
4.如图,已知四边形ABCD是空间四边形,E,H分别是边AB,AD的中点,F,G分别是边CB,CD上的点,且,.求证:四边形EFGH是梯形.
答案:1.D 2.C 3.1 4.略
课堂小结
知识总结
