苏科版数学八年级上册第1章 全等三角形单元 复习训练(word版含答案)
文档属性
| 名称 | 苏科版数学八年级上册第1章 全等三角形单元 复习训练(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 204.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-22 18:00:06 | ||
图片预览



文档简介
第1章单元复习训练
一、选择题
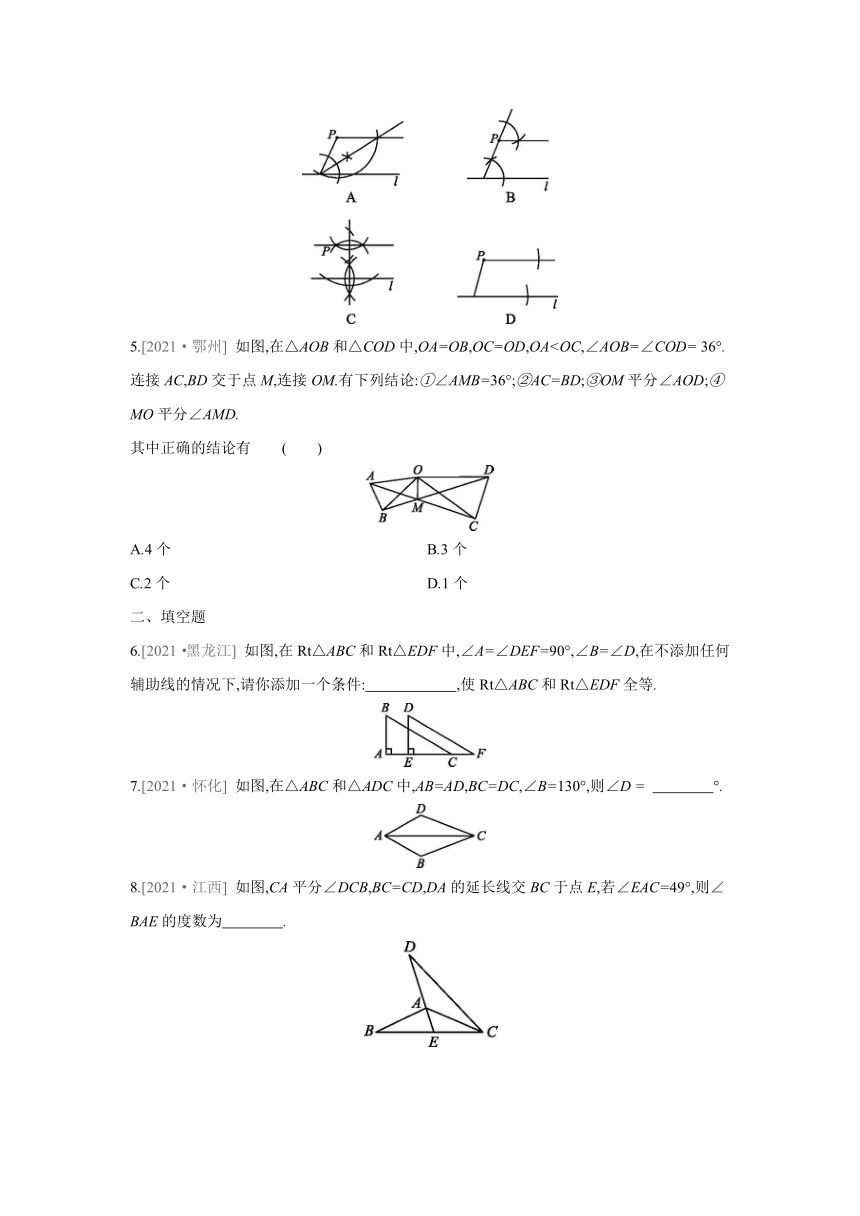
1.[2021·永州] 如图,已知AB=DC,∠ABC=∠DCB,能直接判断△ABC≌△DCB的方法是 ( )
A.SAS B.AAS
C.SSS D.ASA
2.[2021·淄博] 如图,若△ABC≌△ADE,则下列结论中一定成立的是 ( )
A.AC=DE B.∠BAD=∠CAE
C.AB=AE D.∠ABC=∠AED
3.[2021·襄阳] 如图,在Rt△ABC中,∠ABC=90°,根据尺规作图的痕迹判断以下结论错误的是 ( )
A.DB=DE
B.AB=AE
C.∠EDC=∠BAC
D.∠DAC=∠C
4.[2021·衢州] 过直线l外一点P作直线l的平行线,下列尺规作图中错误的是 ( )
5.[2021·鄂州] 如图,在△AOB和△COD中,OA=OB,OC=OD,OA其中正确的结论有 ( )
A.4个 B.3个
C.2个 D.1个
二、填空题
6.[2021·黑龙江] 如图,在Rt△ABC和Rt△EDF中,∠A=∠DEF=90°,∠B=∠D,在不添加任何辅助线的情况下,请你添加一个条件: ,使Rt△ABC和Rt△EDF全等.
7.[2021·怀化] 如图,在△ABC和△ADC中,AB=AD,BC=DC,∠B=130°,则∠D = °.
8.[2021·江西] 如图,CA平分∠DCB,BC=CD,DA的延长线交BC于点E,若∠EAC=49°,则∠BAE的度数为 .
9.[2021·葫芦岛] 如图,在△ABC中,AB=5,AC=8,BC=9,以点A为圆心,适当的长为半径作弧,交AB于点M,交AC于点N.分别以点M,N为圆心,大于MN的长为半径作弧,两弧在∠BAC的内部相交于点G,作射线AG,交BC于点D,点F在AC边上,AF=AB,连接DF,则△CDF的周长为 .
10.[2021·太仓期末] 如图,在△ABC中,∠ACB=90°,AC=6 cm,BC=8 cm,直线l经过点C且与边AB相交.动点P从点A出发沿A→C→B路径向终点B运动;动点Q从点B出发沿B→C→A路径向终点A运动.点P和点Q的速度分别为2 cm/s和3 cm/s,两点同时出发并开始计时,当点P到达终点B时计时结束.在某时刻分别过点P和点Q作PE⊥l于点E,QF⊥l于点F,设运动时间为t s,则当t= 时,△PEC与△QFC全等.
三、解答题
11.[2021·西藏] 如图,在△ABC中,D为BC边上的一点,AD=AC,以线段AD为边作△ADE,使得AE=AB,∠BAE=∠CAD.
求证:DE=CB.
12.[2021·常州] 已知:如图,点A,B,C,D在一条直线上,EA∥FB,EA=FB,AB=CD.
(1)求证:∠E=∠F;
(2)若∠A=40°,∠D=80°,求∠E的度数.
13.[2021·镇江] 如图,AC是四边形ABCD的对角线,∠1=∠B,点E,F分别在AB,BC上,BE=CD,BF=CA,连接EF.
(1)求证:∠D=∠2;
(2)若EF∥AC,∠D=78°,求∠BAC的度数.
14.[2021·南充] 如图,点C在线段BD上,且AB⊥BD,DE⊥BD,AC⊥CE,BC=DE.求证:AB=CD.
15.[2021·盐城滨海县一模] 如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8.
(1)尺规作图:不写作法,保留作图痕迹.
①作∠ACB的平分线,交斜边AB于点D;
②过点D作BC的垂线,垂足为E.
(2)在(1)作出的图形中,求DE的长.
答案
1.A
2.B ∵△ABC≌△ADE,∴AC=AE,AB=AD,∠ABC=∠ADE,∠BAC=∠DAE,∴∠BAC-∠DAC=∠DAE-∠DAC,即∠BAD=∠CAE.故A,C,D选项错误,B选项正确.故选B.
3.D 由作图可知∠DAE=∠DAB,∠DEA=∠B=90°.
又∵AD=AD,
∴△ADE≌△ADB(AAS),
∴DB=DE,AB=AE.
∵∠AED+∠B=180°,
∴∠BAC+∠BDE=180°.
∵∠EDC+∠BDE=180°,
∴∠EDC=∠BAC.
故选项A,B,C正确.故选D.
4.D
5.B ∵∠AOB=∠COD=36°,
∴∠AOB+∠BOC=∠COD+∠BOC,
即∠AOC=∠BOD.
在△AOC和△BOD中,
∴△AOC≌△BOD(SAS),
∴∠OAC=∠OBD,AC=BD,故②正确;
由三角形的外角性质得
∠AMB+∠OBD=∠OAC+∠AOB,
∴∠AMB=∠AOB=36°,故①正确;
过点O作OG⊥AM于点G,OH⊥DM于点H,如图所示,则∠OGA=∠OHB=90°.
∵△AOC≌△BOD,
∴S△AOC=S△BOD,
∴OG=OH.
在Rt△OGM和Rt△OHM中,
∴Rt△OGM≌Rt△OHM(HL),
∴∠GMO=∠HMO.
∴MO平分∠AMD,故④正确;
假设OM平分∠AOD,则∠DOM=∠AOM.
在△AMO与△DMO中,
∴△AMO≌△DMO(ASA),
∴AO=OD.
∵OC=OD,∴OA=OC,
而OA故选B.
6.答案不唯一,如图AB=ED
7.130 在△ADC和△ABC中,
∴△ADC≌△ABC(SSS),∴∠D=∠B.
∵∠B=130°,∴∠D=130°.
故答案为130.
8.82°
9.12 ∵AB=5,AC=8,AF=AB,
∴FC=AC-AF=8-5=3.
由作图方法可得AD平分∠BAC,
∴∠BAD=∠CAD.
在△ABD和△AFD中,
∴△ABD≌△AFD(SAS),
∴BD=DF,
∴△CDF的周长为DF+FC+DC=BD+DC+FC=BC+FC=9+3=12.
10.2或或6 由题意得AP=2t,BQ=3t.
①如图 ,当△PEC≌△CFQ时,
则CP=CQ,
即6-2t=8-3t,
解得t=2.
②如图 ,当点P与点Q重合时,
∴△PEC≌△QFC,
则CP=CQ,
∴6-2t=3t-8,解得t=.
③如图 ,当点Q与点A重合时,△PEC≌△CFQ,
则CP=CQ,
即2t-6=6,解得t=6.
综上所述,当t=2或或6时,△PEC与△QFC全等.
11.证明:∵∠BAE=∠CAD,
∴∠BAE+∠BAD=∠CAD+∠BAD,
即∠DAE=∠CAB.
在△ADE和△ACB中,
∴△ADE≌△ACB(SAS),
∴DE=CB.
12.解:(1)证明:∵EA∥FB,
∴∠A=∠FBD.
∵AB=CD,∴AB+BC=CD+BC,
即AC=BD.
在△EAC和△FBD中,
∴△EAC≌△FBD(SAS),
∴∠E=∠F.
(2)∵△EAC≌△FBD,
∴∠ECA=∠D=80°.
∵∠A=40°,
∴∠E=180°-40°-80°=60°.
13.解:(1)证明:在△BEF和△CDA中,
∴△BEF≌△CDA(SAS),
∴∠D=∠2.
(2)∵∠D=∠2,∠D=78°,∴∠2=78°.
∵EF∥AC,∴∠BAC=∠2=78°.
14.证明:∵AB⊥BD,DE⊥BD,AC⊥CE,
∴∠ACE=∠ABC=∠CDE=90°,
∴∠ACB+∠ECD=90°,∠ECD+∠CED=90°,
∴∠ACB=∠CED.
在△ABC和△CDE中,
∴△ABC≌△CDE(ASA),
∴AB=CD.
15.解:(1)①如图,CD即为所求.
②如图,DE即为所求.
(2)如图,过点D作DF⊥AC于点F.
∵CD平分∠ACB,
∴∠ECD=∠FCD.
在△ECD和△FCD中,
∴△ECD≌△FCD(AAS),
∴DE=DF.
∵∠ACB=90°,AC=6,BC=8.
∴S△ABC=S△ACD+S△BCD,
即AC·BC=AC·DF+BC·DE,
∴6×8=6DE+8DE,
解得DE=.
一、选择题
1.[2021·永州] 如图,已知AB=DC,∠ABC=∠DCB,能直接判断△ABC≌△DCB的方法是 ( )
A.SAS B.AAS
C.SSS D.ASA
2.[2021·淄博] 如图,若△ABC≌△ADE,则下列结论中一定成立的是 ( )
A.AC=DE B.∠BAD=∠CAE
C.AB=AE D.∠ABC=∠AED
3.[2021·襄阳] 如图,在Rt△ABC中,∠ABC=90°,根据尺规作图的痕迹判断以下结论错误的是 ( )
A.DB=DE
B.AB=AE
C.∠EDC=∠BAC
D.∠DAC=∠C
4.[2021·衢州] 过直线l外一点P作直线l的平行线,下列尺规作图中错误的是 ( )
5.[2021·鄂州] 如图,在△AOB和△COD中,OA=OB,OC=OD,OA
A.4个 B.3个
C.2个 D.1个
二、填空题
6.[2021·黑龙江] 如图,在Rt△ABC和Rt△EDF中,∠A=∠DEF=90°,∠B=∠D,在不添加任何辅助线的情况下,请你添加一个条件: ,使Rt△ABC和Rt△EDF全等.
7.[2021·怀化] 如图,在△ABC和△ADC中,AB=AD,BC=DC,∠B=130°,则∠D = °.
8.[2021·江西] 如图,CA平分∠DCB,BC=CD,DA的延长线交BC于点E,若∠EAC=49°,则∠BAE的度数为 .
9.[2021·葫芦岛] 如图,在△ABC中,AB=5,AC=8,BC=9,以点A为圆心,适当的长为半径作弧,交AB于点M,交AC于点N.分别以点M,N为圆心,大于MN的长为半径作弧,两弧在∠BAC的内部相交于点G,作射线AG,交BC于点D,点F在AC边上,AF=AB,连接DF,则△CDF的周长为 .
10.[2021·太仓期末] 如图,在△ABC中,∠ACB=90°,AC=6 cm,BC=8 cm,直线l经过点C且与边AB相交.动点P从点A出发沿A→C→B路径向终点B运动;动点Q从点B出发沿B→C→A路径向终点A运动.点P和点Q的速度分别为2 cm/s和3 cm/s,两点同时出发并开始计时,当点P到达终点B时计时结束.在某时刻分别过点P和点Q作PE⊥l于点E,QF⊥l于点F,设运动时间为t s,则当t= 时,△PEC与△QFC全等.
三、解答题
11.[2021·西藏] 如图,在△ABC中,D为BC边上的一点,AD=AC,以线段AD为边作△ADE,使得AE=AB,∠BAE=∠CAD.
求证:DE=CB.
12.[2021·常州] 已知:如图,点A,B,C,D在一条直线上,EA∥FB,EA=FB,AB=CD.
(1)求证:∠E=∠F;
(2)若∠A=40°,∠D=80°,求∠E的度数.
13.[2021·镇江] 如图,AC是四边形ABCD的对角线,∠1=∠B,点E,F分别在AB,BC上,BE=CD,BF=CA,连接EF.
(1)求证:∠D=∠2;
(2)若EF∥AC,∠D=78°,求∠BAC的度数.
14.[2021·南充] 如图,点C在线段BD上,且AB⊥BD,DE⊥BD,AC⊥CE,BC=DE.求证:AB=CD.
15.[2021·盐城滨海县一模] 如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8.
(1)尺规作图:不写作法,保留作图痕迹.
①作∠ACB的平分线,交斜边AB于点D;
②过点D作BC的垂线,垂足为E.
(2)在(1)作出的图形中,求DE的长.
答案
1.A
2.B ∵△ABC≌△ADE,∴AC=AE,AB=AD,∠ABC=∠ADE,∠BAC=∠DAE,∴∠BAC-∠DAC=∠DAE-∠DAC,即∠BAD=∠CAE.故A,C,D选项错误,B选项正确.故选B.
3.D 由作图可知∠DAE=∠DAB,∠DEA=∠B=90°.
又∵AD=AD,
∴△ADE≌△ADB(AAS),
∴DB=DE,AB=AE.
∵∠AED+∠B=180°,
∴∠BAC+∠BDE=180°.
∵∠EDC+∠BDE=180°,
∴∠EDC=∠BAC.
故选项A,B,C正确.故选D.
4.D
5.B ∵∠AOB=∠COD=36°,
∴∠AOB+∠BOC=∠COD+∠BOC,
即∠AOC=∠BOD.
在△AOC和△BOD中,
∴△AOC≌△BOD(SAS),
∴∠OAC=∠OBD,AC=BD,故②正确;
由三角形的外角性质得
∠AMB+∠OBD=∠OAC+∠AOB,
∴∠AMB=∠AOB=36°,故①正确;
过点O作OG⊥AM于点G,OH⊥DM于点H,如图所示,则∠OGA=∠OHB=90°.
∵△AOC≌△BOD,
∴S△AOC=S△BOD,
∴OG=OH.
在Rt△OGM和Rt△OHM中,
∴Rt△OGM≌Rt△OHM(HL),
∴∠GMO=∠HMO.
∴MO平分∠AMD,故④正确;
假设OM平分∠AOD,则∠DOM=∠AOM.
在△AMO与△DMO中,
∴△AMO≌△DMO(ASA),
∴AO=OD.
∵OC=OD,∴OA=OC,
而OA
6.答案不唯一,如图AB=ED
7.130 在△ADC和△ABC中,
∴△ADC≌△ABC(SSS),∴∠D=∠B.
∵∠B=130°,∴∠D=130°.
故答案为130.
8.82°
9.12 ∵AB=5,AC=8,AF=AB,
∴FC=AC-AF=8-5=3.
由作图方法可得AD平分∠BAC,
∴∠BAD=∠CAD.
在△ABD和△AFD中,
∴△ABD≌△AFD(SAS),
∴BD=DF,
∴△CDF的周长为DF+FC+DC=BD+DC+FC=BC+FC=9+3=12.
10.2或或6 由题意得AP=2t,BQ=3t.
①如图 ,当△PEC≌△CFQ时,
则CP=CQ,
即6-2t=8-3t,
解得t=2.
②如图 ,当点P与点Q重合时,
∴△PEC≌△QFC,
则CP=CQ,
∴6-2t=3t-8,解得t=.
③如图 ,当点Q与点A重合时,△PEC≌△CFQ,
则CP=CQ,
即2t-6=6,解得t=6.
综上所述,当t=2或或6时,△PEC与△QFC全等.
11.证明:∵∠BAE=∠CAD,
∴∠BAE+∠BAD=∠CAD+∠BAD,
即∠DAE=∠CAB.
在△ADE和△ACB中,
∴△ADE≌△ACB(SAS),
∴DE=CB.
12.解:(1)证明:∵EA∥FB,
∴∠A=∠FBD.
∵AB=CD,∴AB+BC=CD+BC,
即AC=BD.
在△EAC和△FBD中,
∴△EAC≌△FBD(SAS),
∴∠E=∠F.
(2)∵△EAC≌△FBD,
∴∠ECA=∠D=80°.
∵∠A=40°,
∴∠E=180°-40°-80°=60°.
13.解:(1)证明:在△BEF和△CDA中,
∴△BEF≌△CDA(SAS),
∴∠D=∠2.
(2)∵∠D=∠2,∠D=78°,∴∠2=78°.
∵EF∥AC,∴∠BAC=∠2=78°.
14.证明:∵AB⊥BD,DE⊥BD,AC⊥CE,
∴∠ACE=∠ABC=∠CDE=90°,
∴∠ACB+∠ECD=90°,∠ECD+∠CED=90°,
∴∠ACB=∠CED.
在△ABC和△CDE中,
∴△ABC≌△CDE(ASA),
∴AB=CD.
15.解:(1)①如图,CD即为所求.
②如图,DE即为所求.
(2)如图,过点D作DF⊥AC于点F.
∵CD平分∠ACB,
∴∠ECD=∠FCD.
在△ECD和△FCD中,
∴△ECD≌△FCD(AAS),
∴DE=DF.
∵∠ACB=90°,AC=6,BC=8.
∴S△ABC=S△ACD+S△BCD,
即AC·BC=AC·DF+BC·DE,
∴6×8=6DE+8DE,
解得DE=.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
