苏科版数学八年级上册第1章 全等三角形 单元综合测试(word,含答案)
文档属性
| 名称 | 苏科版数学八年级上册第1章 全等三角形 单元综合测试(word,含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 166.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-22 20:55:46 | ||
图片预览


文档简介
第1章 全等三角形 单元综合测试
一、选择题(每小题4分,共24分)
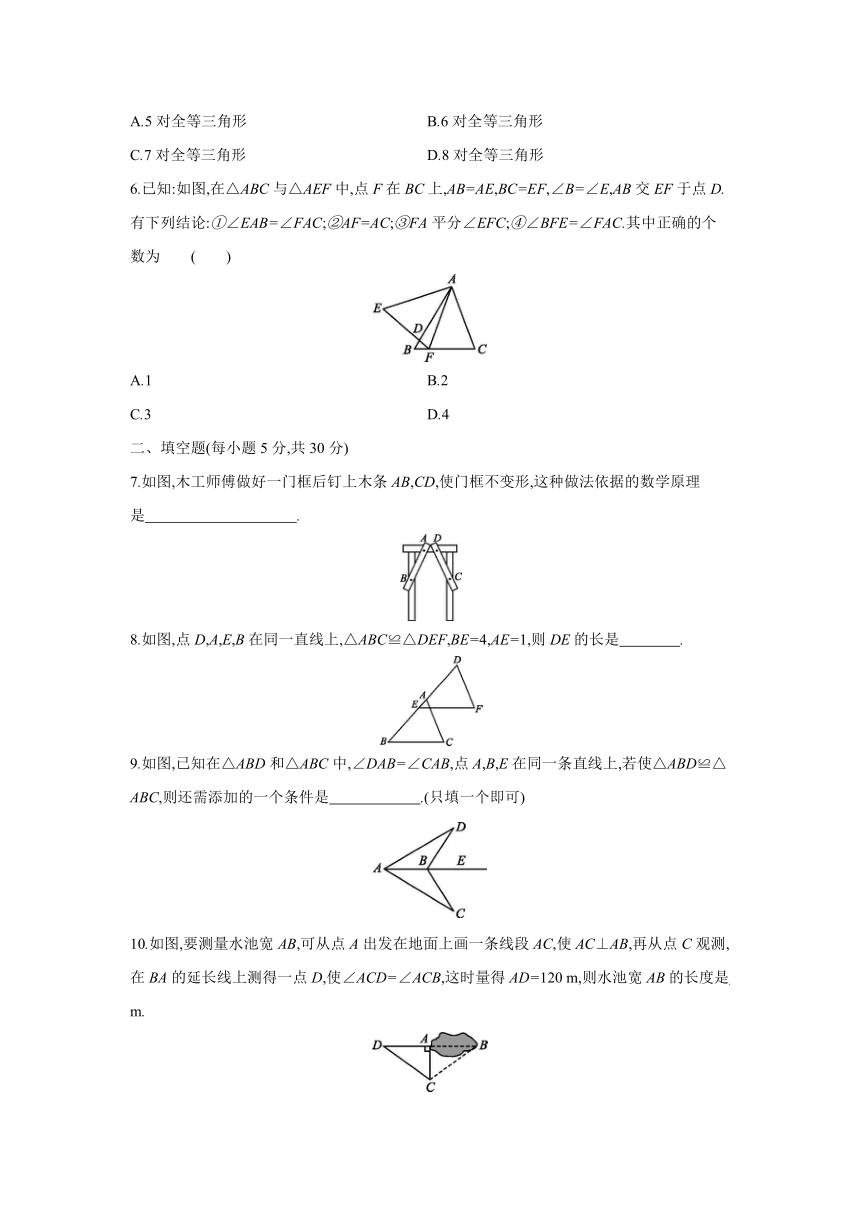
1.下列各组的两个图形属于全等图形的是 ( )
2.如图所示,△ABC≌△ECD,∠A=48°,∠D=62°,点B,C,D在同一条直线上,则图中∠ACE的度数是 ( )
A.38° B.48°
C.62° D.132°
3.如图所示,已知AE=CF,BE=DF,要使△ABE≌△CDF,可以添加的一个条件是 ( )
A.∠BAC=∠ACD B.∠ABE=∠CDF
C.∠DAC=∠BCA D.∠AEB=∠CFD
4.如图,小敏做了一个角平分仪ABCD,其中AB=AD,BC=DC,将仪器上的点A与∠PRQ的顶点R重合,调整AB和AD,使它们分别落在角的两边上,过点A,C画一条射线AE,AE就是∠PRQ的平分线,此角平分仪的画图原理是 ( )
A.SSS B.SAS
C.ASA D.AAS
5.如图,AB∥CD,AD∥BC,AC与BD相交于点O,AE⊥BD,CF⊥BD,垂足分别是E,F,则图中共有 ( )
A.5对全等三角形 B.6对全等三角形
C.7对全等三角形 D.8对全等三角形
6.已知:如图,在△ABC与△AEF中,点F在BC上,AB=AE,BC=EF,∠B=∠E,AB交EF于点D.有下列结论:①∠EAB=∠FAC;②AF=AC;③FA平分∠EFC;④∠BFE=∠FAC.其中正确的个数为 ( )
A.1 B.2
C.3 D.4
二、填空题(每小题5分,共30分)
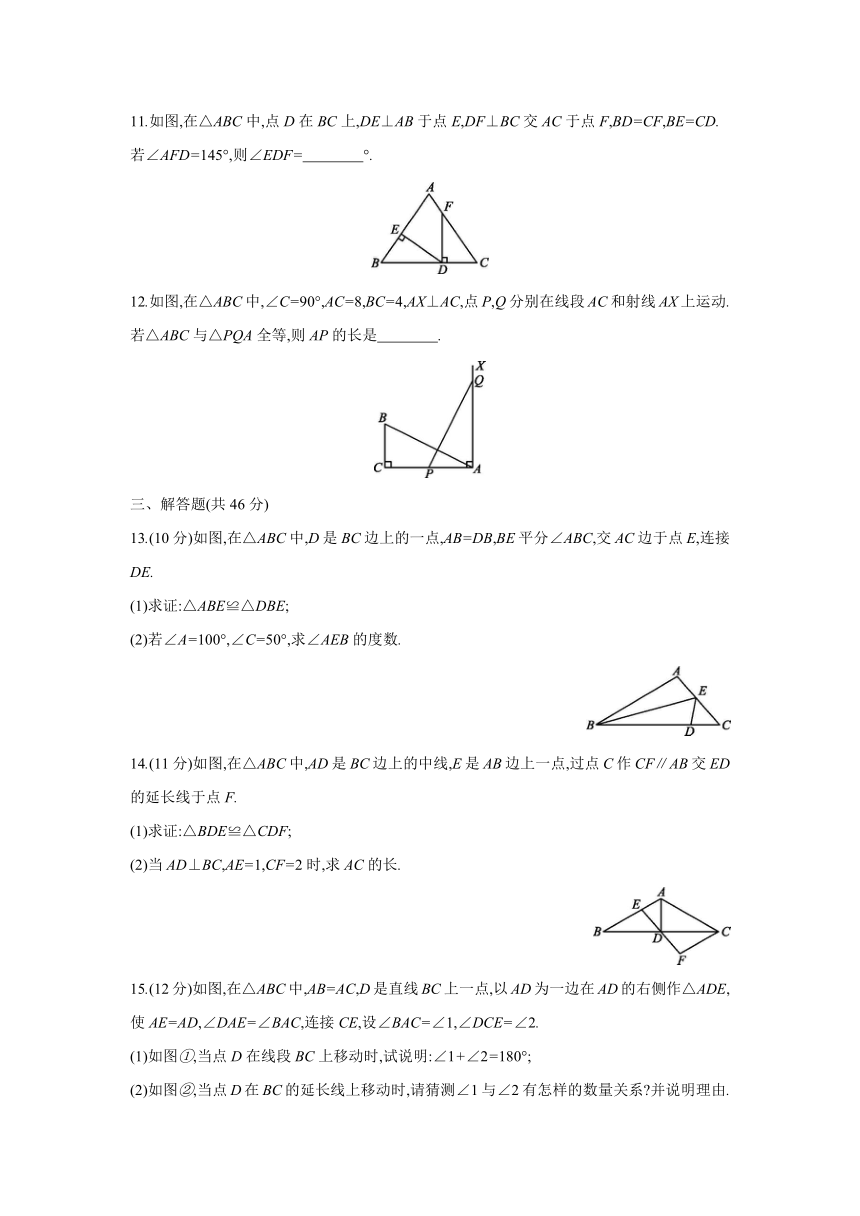
7.如图,木工师傅做好一门框后钉上木条AB,CD,使门框不变形,这种做法依据的数学原理是 .
8.如图,点D,A,E,B在同一直线上,△ABC≌△DEF,BE=4,AE=1,则DE的长是 .
9.如图,已知在△ABD和△ABC中,∠DAB=∠CAB,点A,B,E在同一条直线上,若使△ABD≌△ABC,则还需添加的一个条件是 .(只填一个即可)
10.如图,要测量水池宽AB,可从点A出发在地面上画一条线段AC,使AC⊥AB,再从点C观测,在BA的延长线上测得一点D,使∠ACD=∠ACB,这时量得AD=120 m,则水池宽AB的长度是 m.
11.如图,在△ABC中,点D在BC上,DE⊥AB于点E,DF⊥BC交AC于点F,BD=CF,BE=CD.若∠AFD=145°,则∠EDF= °.
12.如图,在△ABC中,∠C=90°,AC=8,BC=4,AX⊥AC,点P,Q分别在线段AC和射线AX上运动.若△ABC与△PQA全等,则AP的长是 .
三、解答题(共46分)
13.(10分)如图,在△ABC中,D是BC边上的一点,AB=DB,BE平分∠ABC,交AC边于点E,连接DE.
(1)求证:△ABE≌△DBE;
(2)若∠A=100°,∠C=50°,求∠AEB的度数.
14.(11分)如图,在△ABC中,AD是BC边上的中线,E是AB边上一点,过点C作CF∥AB交ED的延长线于点F.
(1)求证:△BDE≌△CDF;
(2)当AD⊥BC,AE=1,CF=2时,求AC的长.
15.(12分)如图,在△ABC中,AB=AC,D是直线BC上一点,以AD为一边在AD的右侧作△ADE,使AE=AD,∠DAE=∠BAC,连接CE,设∠BAC=∠1,∠DCE=∠2.
(1)如图①,当点D在线段BC上移动时,试说明:∠1+∠2=180°;
(2)如图②,当点D在BC的延长线上移动时,请猜测∠1与∠2有怎样的数量关系 并说明理由.
16.(13分)CD是经过∠BCA的顶点C的一条直线,CA=BC,E,F是直线CD上的两点,且∠BEC=∠CFA=α.
(1)若直线CD经过∠BCA的内部,且点E,F在射线CD上,请解决下列问题:
①如图(a)所示,若∠BCA=90°,α=90°,
则BE CF,EF |BE-AF|(填“>”“<”或“=”);
②如图(b),若0°<∠BCA<180°,请添加一个关于α与∠BCA关系的条件: ,使①中的两个结论仍然成立,并证明这两个结论成立.
(2)如图(c),若直线CD经过∠BCA的外部,α=∠BCA,请提出EF,BE,AF三条线段之间数量关系的合理猜想(不要求证明).
答案
1.D A项,嘴巴不能完全重合,故本选项不符合题意;
B项,两个正方形的边长不相等,不能完全重合,故本选项不符合题意;
C项,圆内两条相交的线段不能完全重合,故本选项不符合题意;
D项,两个图形能够完全重合,故本选项符合题意.故选D.
2.B
3.D 在△ABE和△CDF中,已经具备AE=CF,BE=DF,只要再添加夹角相等的条件即可.
4.A 在△ABC和△ADC中,∴△ABC≌△ADC(SSS),
∴∠BAC=∠DAC,∴AE是∠PRQ的平分线.故选A.
5.C ∵AB∥CD,AD∥BC,
∴∠ABD=∠CDB,∠ADB=∠CBD,
∠BAC=∠DCA.
在△ABD和△CDB中,
∴△ABD≌△CDB(ASA),
∴AE=CF,
同理:△ABC≌△CDA(ASA),
∴AB=CD,BC=DA.
在△AOB和△COD中,
∴△AOB≌△COD(AAS),
同理:△AOD≌△COB(AAS).
∵AE⊥BD,CF⊥BD,
∴∠AEB=∠AEO=∠CFD=∠CFO=90°.
在△ABE和△CDF中,
∴△ABE≌△CDF(AAS),
∴AE=CF,
同理:△AOE≌△COF(AAS),△ADE≌△CBF(AAS).
故图中共有7对全等三角形.故选C.
6.D 在△ABC和△AEF中,
∴△ABC≌△AEF(SAS),
∴∠EAF=∠BAC,AF=AC,∠C=∠EFA,
∴∠EAB=∠FAC,∠AFC=∠C,
∴∠EFA=∠AFC,
即FA平分∠EFC.
∵∠AFB=∠C+∠FAC=∠EFA+∠BFE,
∴∠BFE=∠FAC.
故①②③④正确.故选D.
7.三角形的稳定性
8.5 ∵BE=4,AE=1,
∴AB=BE+AE=4+1=5.
∵△ABC≌△DEF,
∴DE=AB=5.
9.答案不唯一,图AD=AC
10.120 ∵AC⊥BD,∴∠CAD=∠CAB=90°.又∵CA=CA,∠ACD=∠ACB,∴△ACD≌△ACB(ASA),∴AB=AD=120 m.
11.55 ∵∠CFD+∠AFD=180°,∠AFD=145°,
∴∠CFD=35°.
∵DE⊥AB,DF⊥BC,
∴∠BED=∠CDF=90°.
在Rt△BDE与△Rt△CFD中,
∴Rt△BDE≌△Rt△CFD(HL),
∴∠BDE=∠CFD=35°,
∴∠EDF+∠BDE=∠EDF+35°=90°,
∴∠EDF=55°.
12.4或8 ∵△ABC与△PQA全等,
∴AP=BC=4或AP=AC=8.
故答案为4或8.
13.解:(1)证明:∵BE平分∠ABC,
∴∠ABE=∠DBE.
在△ABE和△DBE中,
∴△ABE≌△DBE(SAS).
(2)∵∠A=100°,∠C=50°,∴∠ABC=30°.
∵BE平分∠ABC,
∴∠ABE=∠DBE=∠ABC=15°.
在△ABE中,∠AEB=180°-∠A-∠ABE=180°-100°-15°=65°.
14.解:(1)证明:∵CF∥AB,
∴∠B=∠FCD,∠BED=∠F.
∵AD是BC边上的中线,∴BD=CD.
在△BDE和△CDF中,
∴△BDE≌△CDF(AAS).
(2)∵△BDE≌△CDF,
∴BE=CF=2.
∴AB=AE+BE=1+2=3.
∵AD⊥BC,∴∠ADB=∠ADC=90°.
在△ADB和△ADC中,
∴△ADB≌△ADC.∴AC=AB=3.
15.解:(1)∵∠DAE=∠BAC,
∴∠BAD=∠CAE.
在△ABD和△ACE中,
∴△ABD≌△ACE(SAS),
∴∠ACE=∠ABD.
∵∠BAC+∠ABD+∠ACB=180°,
∴∠BAC+∠ACB+∠ACE=∠BAC+∠BCE=180°,
∴∠1+∠2=180°.
(2)∠1=∠2.
理由如下:∵∠DAE=∠BAC,
∴∠BAD=∠CAE.
在△ABD和△ACE中,
∴△ABD≌△ACE(SAS),
∴∠ACE=∠ABD.
∵∠BAC+∠ABD+∠ACB=180°,∠ACE+∠ACB+∠DCE=180°,∴∠BAC=∠DCE,
∴∠1=∠2.
16.解:(1)①∵∠BCA=90°,α=90°,
∴∠BCE+∠CBE=90°,
∠BCE+∠ACF=90°.
∴∠CBE=∠ACF.
在△BCE和△CAF中,
∴△BCE≌△CAF.
∴BE=CF,CE=AF.
∴EF=|BE-AF|.
故答案为=,=.
②α+∠BCA=180°
证明:在△BCE中,∠CBE+∠BCE=180°-∠BEC=180°-α.
∵∠BCA=180°-α,
∴∠CBE+∠BCE=∠BCA.
又∵∠ACF+∠BCE=∠BCA,
∴∠CBE=∠ACF.
在△BCE和△CAF中,
∴△BCE≌△CAF(AAS).
∴BE=CF,CE=AF.
又∵EF=|CF-CE|,
∴EF=|BE-AF|.
(2)EF=BE+AF.
一、选择题(每小题4分,共24分)
1.下列各组的两个图形属于全等图形的是 ( )
2.如图所示,△ABC≌△ECD,∠A=48°,∠D=62°,点B,C,D在同一条直线上,则图中∠ACE的度数是 ( )
A.38° B.48°
C.62° D.132°
3.如图所示,已知AE=CF,BE=DF,要使△ABE≌△CDF,可以添加的一个条件是 ( )
A.∠BAC=∠ACD B.∠ABE=∠CDF
C.∠DAC=∠BCA D.∠AEB=∠CFD
4.如图,小敏做了一个角平分仪ABCD,其中AB=AD,BC=DC,将仪器上的点A与∠PRQ的顶点R重合,调整AB和AD,使它们分别落在角的两边上,过点A,C画一条射线AE,AE就是∠PRQ的平分线,此角平分仪的画图原理是 ( )
A.SSS B.SAS
C.ASA D.AAS
5.如图,AB∥CD,AD∥BC,AC与BD相交于点O,AE⊥BD,CF⊥BD,垂足分别是E,F,则图中共有 ( )
A.5对全等三角形 B.6对全等三角形
C.7对全等三角形 D.8对全等三角形
6.已知:如图,在△ABC与△AEF中,点F在BC上,AB=AE,BC=EF,∠B=∠E,AB交EF于点D.有下列结论:①∠EAB=∠FAC;②AF=AC;③FA平分∠EFC;④∠BFE=∠FAC.其中正确的个数为 ( )
A.1 B.2
C.3 D.4
二、填空题(每小题5分,共30分)
7.如图,木工师傅做好一门框后钉上木条AB,CD,使门框不变形,这种做法依据的数学原理是 .
8.如图,点D,A,E,B在同一直线上,△ABC≌△DEF,BE=4,AE=1,则DE的长是 .
9.如图,已知在△ABD和△ABC中,∠DAB=∠CAB,点A,B,E在同一条直线上,若使△ABD≌△ABC,则还需添加的一个条件是 .(只填一个即可)
10.如图,要测量水池宽AB,可从点A出发在地面上画一条线段AC,使AC⊥AB,再从点C观测,在BA的延长线上测得一点D,使∠ACD=∠ACB,这时量得AD=120 m,则水池宽AB的长度是 m.
11.如图,在△ABC中,点D在BC上,DE⊥AB于点E,DF⊥BC交AC于点F,BD=CF,BE=CD.若∠AFD=145°,则∠EDF= °.
12.如图,在△ABC中,∠C=90°,AC=8,BC=4,AX⊥AC,点P,Q分别在线段AC和射线AX上运动.若△ABC与△PQA全等,则AP的长是 .
三、解答题(共46分)
13.(10分)如图,在△ABC中,D是BC边上的一点,AB=DB,BE平分∠ABC,交AC边于点E,连接DE.
(1)求证:△ABE≌△DBE;
(2)若∠A=100°,∠C=50°,求∠AEB的度数.
14.(11分)如图,在△ABC中,AD是BC边上的中线,E是AB边上一点,过点C作CF∥AB交ED的延长线于点F.
(1)求证:△BDE≌△CDF;
(2)当AD⊥BC,AE=1,CF=2时,求AC的长.
15.(12分)如图,在△ABC中,AB=AC,D是直线BC上一点,以AD为一边在AD的右侧作△ADE,使AE=AD,∠DAE=∠BAC,连接CE,设∠BAC=∠1,∠DCE=∠2.
(1)如图①,当点D在线段BC上移动时,试说明:∠1+∠2=180°;
(2)如图②,当点D在BC的延长线上移动时,请猜测∠1与∠2有怎样的数量关系 并说明理由.
16.(13分)CD是经过∠BCA的顶点C的一条直线,CA=BC,E,F是直线CD上的两点,且∠BEC=∠CFA=α.
(1)若直线CD经过∠BCA的内部,且点E,F在射线CD上,请解决下列问题:
①如图(a)所示,若∠BCA=90°,α=90°,
则BE CF,EF |BE-AF|(填“>”“<”或“=”);
②如图(b),若0°<∠BCA<180°,请添加一个关于α与∠BCA关系的条件: ,使①中的两个结论仍然成立,并证明这两个结论成立.
(2)如图(c),若直线CD经过∠BCA的外部,α=∠BCA,请提出EF,BE,AF三条线段之间数量关系的合理猜想(不要求证明).
答案
1.D A项,嘴巴不能完全重合,故本选项不符合题意;
B项,两个正方形的边长不相等,不能完全重合,故本选项不符合题意;
C项,圆内两条相交的线段不能完全重合,故本选项不符合题意;
D项,两个图形能够完全重合,故本选项符合题意.故选D.
2.B
3.D 在△ABE和△CDF中,已经具备AE=CF,BE=DF,只要再添加夹角相等的条件即可.
4.A 在△ABC和△ADC中,∴△ABC≌△ADC(SSS),
∴∠BAC=∠DAC,∴AE是∠PRQ的平分线.故选A.
5.C ∵AB∥CD,AD∥BC,
∴∠ABD=∠CDB,∠ADB=∠CBD,
∠BAC=∠DCA.
在△ABD和△CDB中,
∴△ABD≌△CDB(ASA),
∴AE=CF,
同理:△ABC≌△CDA(ASA),
∴AB=CD,BC=DA.
在△AOB和△COD中,
∴△AOB≌△COD(AAS),
同理:△AOD≌△COB(AAS).
∵AE⊥BD,CF⊥BD,
∴∠AEB=∠AEO=∠CFD=∠CFO=90°.
在△ABE和△CDF中,
∴△ABE≌△CDF(AAS),
∴AE=CF,
同理:△AOE≌△COF(AAS),△ADE≌△CBF(AAS).
故图中共有7对全等三角形.故选C.
6.D 在△ABC和△AEF中,
∴△ABC≌△AEF(SAS),
∴∠EAF=∠BAC,AF=AC,∠C=∠EFA,
∴∠EAB=∠FAC,∠AFC=∠C,
∴∠EFA=∠AFC,
即FA平分∠EFC.
∵∠AFB=∠C+∠FAC=∠EFA+∠BFE,
∴∠BFE=∠FAC.
故①②③④正确.故选D.
7.三角形的稳定性
8.5 ∵BE=4,AE=1,
∴AB=BE+AE=4+1=5.
∵△ABC≌△DEF,
∴DE=AB=5.
9.答案不唯一,图AD=AC
10.120 ∵AC⊥BD,∴∠CAD=∠CAB=90°.又∵CA=CA,∠ACD=∠ACB,∴△ACD≌△ACB(ASA),∴AB=AD=120 m.
11.55 ∵∠CFD+∠AFD=180°,∠AFD=145°,
∴∠CFD=35°.
∵DE⊥AB,DF⊥BC,
∴∠BED=∠CDF=90°.
在Rt△BDE与△Rt△CFD中,
∴Rt△BDE≌△Rt△CFD(HL),
∴∠BDE=∠CFD=35°,
∴∠EDF+∠BDE=∠EDF+35°=90°,
∴∠EDF=55°.
12.4或8 ∵△ABC与△PQA全等,
∴AP=BC=4或AP=AC=8.
故答案为4或8.
13.解:(1)证明:∵BE平分∠ABC,
∴∠ABE=∠DBE.
在△ABE和△DBE中,
∴△ABE≌△DBE(SAS).
(2)∵∠A=100°,∠C=50°,∴∠ABC=30°.
∵BE平分∠ABC,
∴∠ABE=∠DBE=∠ABC=15°.
在△ABE中,∠AEB=180°-∠A-∠ABE=180°-100°-15°=65°.
14.解:(1)证明:∵CF∥AB,
∴∠B=∠FCD,∠BED=∠F.
∵AD是BC边上的中线,∴BD=CD.
在△BDE和△CDF中,
∴△BDE≌△CDF(AAS).
(2)∵△BDE≌△CDF,
∴BE=CF=2.
∴AB=AE+BE=1+2=3.
∵AD⊥BC,∴∠ADB=∠ADC=90°.
在△ADB和△ADC中,
∴△ADB≌△ADC.∴AC=AB=3.
15.解:(1)∵∠DAE=∠BAC,
∴∠BAD=∠CAE.
在△ABD和△ACE中,
∴△ABD≌△ACE(SAS),
∴∠ACE=∠ABD.
∵∠BAC+∠ABD+∠ACB=180°,
∴∠BAC+∠ACB+∠ACE=∠BAC+∠BCE=180°,
∴∠1+∠2=180°.
(2)∠1=∠2.
理由如下:∵∠DAE=∠BAC,
∴∠BAD=∠CAE.
在△ABD和△ACE中,
∴△ABD≌△ACE(SAS),
∴∠ACE=∠ABD.
∵∠BAC+∠ABD+∠ACB=180°,∠ACE+∠ACB+∠DCE=180°,∴∠BAC=∠DCE,
∴∠1=∠2.
16.解:(1)①∵∠BCA=90°,α=90°,
∴∠BCE+∠CBE=90°,
∠BCE+∠ACF=90°.
∴∠CBE=∠ACF.
在△BCE和△CAF中,
∴△BCE≌△CAF.
∴BE=CF,CE=AF.
∴EF=|BE-AF|.
故答案为=,=.
②α+∠BCA=180°
证明:在△BCE中,∠CBE+∠BCE=180°-∠BEC=180°-α.
∵∠BCA=180°-α,
∴∠CBE+∠BCE=∠BCA.
又∵∠ACF+∠BCE=∠BCA,
∴∠CBE=∠ACF.
在△BCE和△CAF中,
∴△BCE≌△CAF(AAS).
∴BE=CF,CE=AF.
又∵EF=|CF-CE|,
∴EF=|BE-AF|.
(2)EF=BE+AF.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
