苏科版数学八年级上册第6章 一次函数 单元综合测试(word,含答案)
文档属性
| 名称 | 苏科版数学八年级上册第6章 一次函数 单元综合测试(word,含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 166.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-22 21:00:36 | ||
图片预览


文档简介
第6章 一次函数 单元综合测试
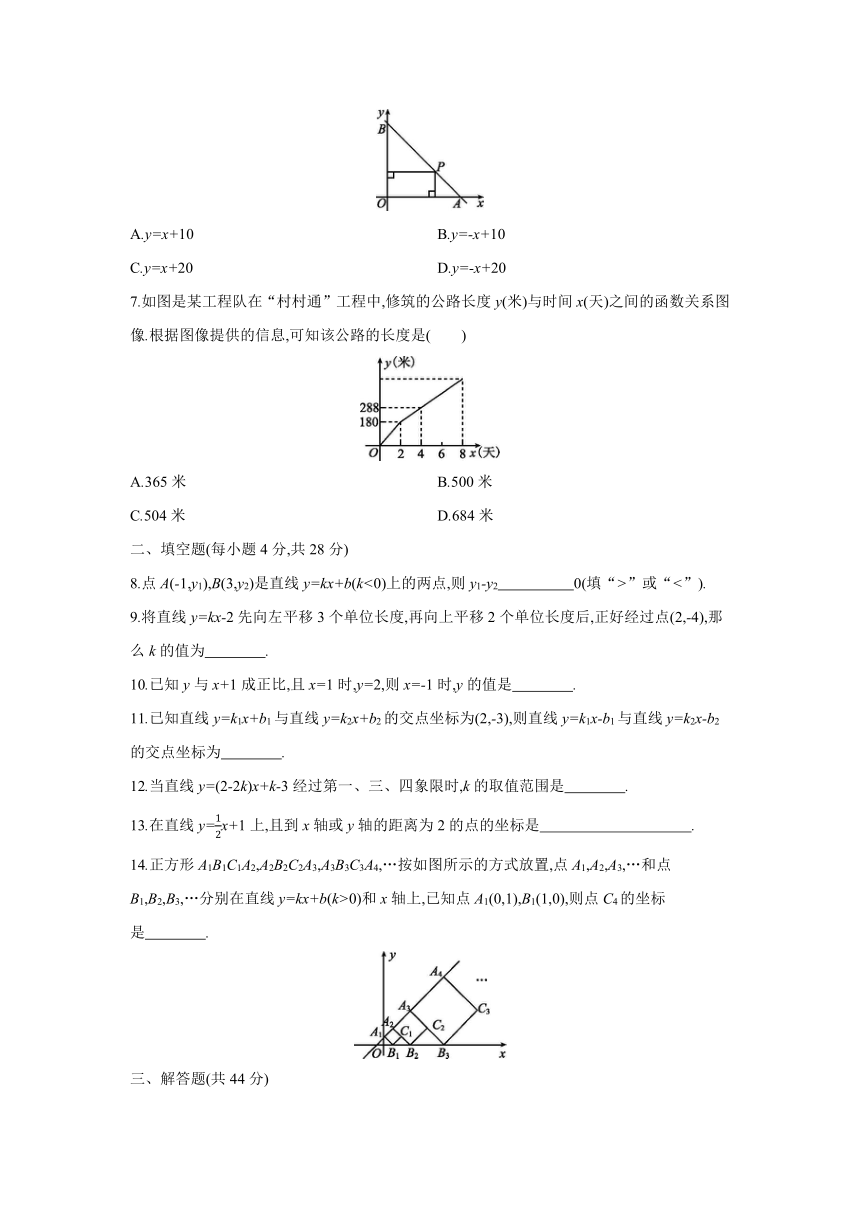
一、选择题(每小题4分,共28分)
1.下列函数表达式:①y=-x,②y=3x+11,③y=x2+x+1,④y=中,属于一次函数的有( )
A.1个 B.2个
C.3个 D.4个
2.一次函数y=kx+3(k≠0)的函数值y随x的增大而增大,它的图像不经过的象限是 ( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
3.若b>0,则一次函数y=-x+b的图像大致是 ( )
4.如图,直线l是一次函数y=kx+b的图像,若点A(3,m)在直线l上,则m的值是 ( )
A.-5 B.
C. D.7
5.如图,函数y=2x和y=ax+4的图像相交于点A(m,3),则不等式2xA.x< B.x<3
C.x> D.x>3
6.如图,一直线与两坐标轴的正半轴分别交于点A,B,P是线段AB上任意一点(不包括端点),过点P分别作两坐标轴的垂线,与两坐标轴围成的长方形的周长为20,则该直线的函数表达式是 ( )
A.y=x+10 B.y=-x+10
C.y=x+20 D.y=-x+20
7.如图是某工程队在“村村通”工程中,修筑的公路长度y(米)与时间x(天)之间的函数关系图像.根据图像提供的信息,可知该公路的长度是( )
A.365米 B.500米
C.504米 D.684米
二、填空题(每小题4分,共28分)
8.点A(-1,y1),B(3,y2)是直线y=kx+b(k<0)上的两点,则y1-y2 0(填“>”或“<”).
9.将直线y=kx-2先向左平移3个单位长度,再向上平移2个单位长度后,正好经过点(2,-4),那么k的值为 .
10.已知y与x+1成正比,且x=1时,y=2,则x=-1时,y的值是 .
11.已知直线y=k1x+b1与直线y=k2x+b2的交点坐标为(2,-3),则直线y=k1x-b1与直线y=k2x-b2的交点坐标为 .
12.当直线y=(2-2k)x+k-3经过第一、三、四象限时,k的取值范围是 .
13.在直线y=x+1上,且到x轴或y轴的距离为2的点的坐标是 .
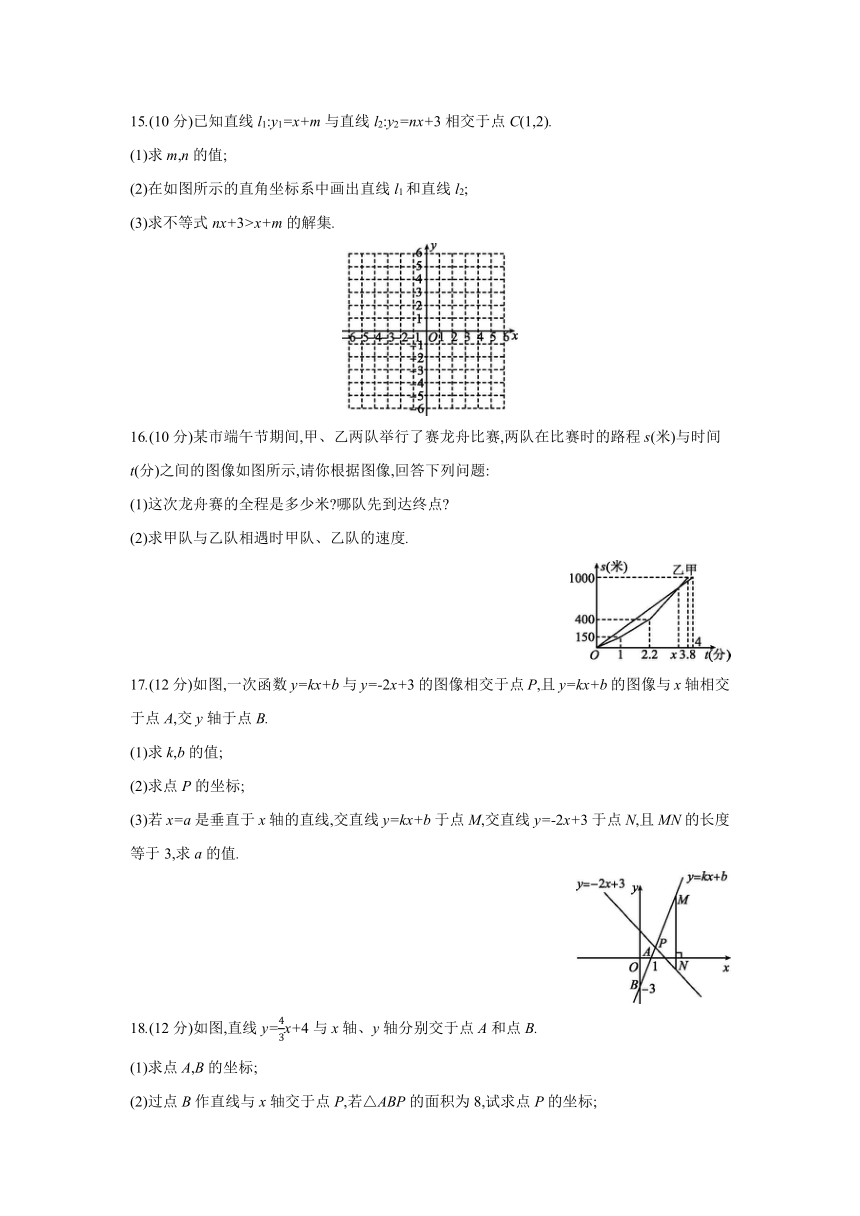
14.正方形A1B1C1A2,A2B2C2A3,A3B3C3A4,…按如图所示的方式放置,点A1,A2,A3,…和点B1,B2,B3,…分别在直线y=kx+b(k>0)和x轴上,已知点A1(0,1),B1(1,0),则点C4的坐标是 .
三、解答题(共44分)
15.(10分)已知直线l1:y1=x+m与直线l2:y2=nx+3相交于点C(1,2).
(1)求m,n的值;
(2)在如图所示的直角坐标系中画出直线l1和直线l2;
(3)求不等式nx+3>x+m的解集.
16.(10分)某市端午节期间,甲、乙两队举行了赛龙舟比赛,两队在比赛时的路程s(米)与时间t(分)之间的图像如图所示,请你根据图像,回答下列问题:
(1)这次龙舟赛的全程是多少米 哪队先到达终点
(2)求甲队与乙队相遇时甲队、乙队的速度.
17.(12分)如图,一次函数y=kx+b与y=-2x+3的图像相交于点P,且y=kx+b的图像与x轴相交于点A,交y轴于点B.
(1)求k,b的值;
(2)求点P的坐标;
(3)若x=a是垂直于x轴的直线,交直线y=kx+b于点M,交直线y=-2x+3于点N,且MN的长度等于3,求a的值.
18.(12分)如图,直线y=x+4与x轴、y轴分别交于点A和点B.
(1)求点A,B的坐标;
(2)过点B作直线与x轴交于点P,若△ABP的面积为8,试求点P的坐标;
(3)M是OB上的一点,若将△ABM沿AM折叠,点B恰好落在x轴上的点B1处,求出点M的坐标;
(4)点C在y轴上,连接AC,若△ABC是以AB为腰的等腰三角形,请直接写出点C的坐标.
答案
1.B ①②是一次函数.故选B.
2.D ∵一次函数y=kx+3(k≠0)的函数值y随x的增大而增大,∴k>0.∵该函数图像过点(0,3),∴该函数的图像经过第一、二、三象限,不经过第四象限.故选D.
3.C 因为一次函数y=-x+b中,k=-1<0,b>0,所以一次函数的图像经过第一、二、四象限.故选C.
4.C 将(-2,0),(0,1)代入y=kx+b,得
解得
所以y=x+1.
将A(3,m)代入,得+1=m.
所以m=.故选C.
5.A 把A(m,3)代入y=2x,得m=,所以点A的坐标为.根据图像可以得出不等式2x6.B 设点P的坐标为(x,y).
因为长方形的周长为20,所以|x|+|y|=10,
即x+y=10.
所以该直线的函数表达式是y=-x+10.
故选B.
7.C 设当x>2时,y与x之间的函数表达式为y=kx+b,则有
解得
所以 y=54x+72.
当x=8时,y=54×8+72=504.
8.> 因为y=kx+b中k<0,所以函数y随x的增大而减小.因为A(-1,y1),B(3,y2)是直线y=kx+b(k<0)上的两点,且-1<3,所以y1>y2.所以y1-y2>0.
9.- 根据题意,将直线y=kx-2先向左平移3个单位长度,再向上平移2个单位长度,得到直线y=kx+3k.因为其正好经过点(2,-4),所以2k+3k=-4.所以k=-.
故答案为-.
10.0 ∵y与x+1成正比,∴设y=k(x+1).∵x=1时,y=2,∴2=k×2,即k=1,∴y=x+1.则当x=-1时,y=-1+1=0.
11.(-2,3) ∵直线y=k1x+b1与直线y=k2x+b2的交点坐标为(2,-3),∴-3=2k1+b1,-3=2k2+b2,∴-b1=2k1+3,-b2=2k2+3,∴直线y=k1x-b1=k1(x+2)+3,直线y=k2x-b2=k2(x+2)+3,∴直线y=k1x-b1与直线y=k2x-b2都经过点(-2,3),∴直线y=k1x-b1与直线y=k2x-b2的交点坐标为(-2,3).
12.k<1 ∵直线y=(2-2k)x+k-3经过第一、三、四象限,∴解得k<1.
13.(2,2)或(-2,0)或(-6,-2)
设点P(m,n)到x轴或y轴的距离为2,则|m|=2或|n|=2,所以m=±2或n=±2.
当m=2时,n=2,此时点P的坐标为(2,2);
当m=-2时,n=0,此时点P的坐标为(-2,0);
当n=2时,m=2,此时点P的坐标为(2,2);
当n=-2时,m=-6,此时点P的坐标为(-6,-2).
故答案为(2,2)或(-2,0)或(-6,-2).
14.(23,8) 由题意可知点A1的纵坐标为1,点A2的纵坐标为2,点A3的纵坐标为4,点A4的纵坐标为8,…
∵点A1和点C1,点A2和点C2,点A3和点C3,点A4和点C4的纵坐标相同,
∴点C1,C2,C3,C4的纵坐标分别为1,2,4,8,
∴根据图像得出C1(2,1),C2(5,2),C3(11,4),
∴直线C1C2的表达式为y=x+.
∵点A4的纵坐标为8,
∴点C4的纵坐标为8.
把y=8代入y=x+,解得x=23,
∴点C4的坐标是(23,8).
15.解:(1)把C(1,2)代入y1=x+m,得1+m=2,解得m=1;
把C(1,2)代入y2=nx+3,得n+3=2,
解得n=-1.
(2)略.
(3)不等式nx+3>x+m的解集为x<1.
16.解:(1)由函数图像可得,这次龙舟赛的全程是1000米,乙队先到达终点.
(2)由图像可得,甲队与乙队相遇时,甲的速度是1000÷4=250(米/分),
乙的速度是(1000-400)÷(3.8-2.2)=600÷1.6=375(米/分),
即甲队与乙队相遇时甲队、乙队的速度分别为250米/分、375米/分.
17.解:(1)由图像可知,一次函数y=kx+b的图像经过点A(1,0),B(0,-3).
把点A,B的坐标代入,得
解得
即k=3,b=-3.
(2)由(1)得一次函数y=kx+b的表达式为y=3x-3,
则有
解得
∴点P的坐标为,.
(3)∵x=a是垂直于x轴的直线,交直线y=kx+b于点M,交直线y=-2x+3于点N,
∴M(a,3a-3),N(a,-2a+3).
∵MN的长度等于3,
∴|3a-3-(-2a+3)|=3,
即|5a-6|=3,
解得a=或a=.
18.解:(1)对于y=x+4,
令y=0,即y=x+4=0,
解得x=-3.
令x=0,则y=4,
故点A,B的坐标分别为(-3,0),(0,4).
(2)设点P(x,0),
则△ABP的面积=×OB×AP=×4×|x+3|=8,
解得x=1或x=-7,
故点P的坐标为(1,0)或(-7,0).
(3)由点A,B的坐标知,OA=3,OB=4,
则AB==5=AB1,
故点B1的坐标为(2,0).
设点M的坐标为(0,m),
由题意得MB=MB1,
即m2+4=(4-m)2,
解得m=1.5,
故点M的坐标为(0,1.5).
(4)设点C(0,t),
则AB=5,AC=.
当AB=BC时,则5=|t-4|,
解得t=9或t=-1,
当AB=AC时,即25=9+t2,
解得t=4(舍去)或t=-4,
故点C的坐标为(0,9)或(0,-1)或(0,-4).
一、选择题(每小题4分,共28分)
1.下列函数表达式:①y=-x,②y=3x+11,③y=x2+x+1,④y=中,属于一次函数的有( )
A.1个 B.2个
C.3个 D.4个
2.一次函数y=kx+3(k≠0)的函数值y随x的增大而增大,它的图像不经过的象限是 ( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
3.若b>0,则一次函数y=-x+b的图像大致是 ( )
4.如图,直线l是一次函数y=kx+b的图像,若点A(3,m)在直线l上,则m的值是 ( )
A.-5 B.
C. D.7
5.如图,函数y=2x和y=ax+4的图像相交于点A(m,3),则不等式2x
C.x> D.x>3
6.如图,一直线与两坐标轴的正半轴分别交于点A,B,P是线段AB上任意一点(不包括端点),过点P分别作两坐标轴的垂线,与两坐标轴围成的长方形的周长为20,则该直线的函数表达式是 ( )
A.y=x+10 B.y=-x+10
C.y=x+20 D.y=-x+20
7.如图是某工程队在“村村通”工程中,修筑的公路长度y(米)与时间x(天)之间的函数关系图像.根据图像提供的信息,可知该公路的长度是( )
A.365米 B.500米
C.504米 D.684米
二、填空题(每小题4分,共28分)
8.点A(-1,y1),B(3,y2)是直线y=kx+b(k<0)上的两点,则y1-y2 0(填“>”或“<”).
9.将直线y=kx-2先向左平移3个单位长度,再向上平移2个单位长度后,正好经过点(2,-4),那么k的值为 .
10.已知y与x+1成正比,且x=1时,y=2,则x=-1时,y的值是 .
11.已知直线y=k1x+b1与直线y=k2x+b2的交点坐标为(2,-3),则直线y=k1x-b1与直线y=k2x-b2的交点坐标为 .
12.当直线y=(2-2k)x+k-3经过第一、三、四象限时,k的取值范围是 .
13.在直线y=x+1上,且到x轴或y轴的距离为2的点的坐标是 .
14.正方形A1B1C1A2,A2B2C2A3,A3B3C3A4,…按如图所示的方式放置,点A1,A2,A3,…和点B1,B2,B3,…分别在直线y=kx+b(k>0)和x轴上,已知点A1(0,1),B1(1,0),则点C4的坐标是 .
三、解答题(共44分)
15.(10分)已知直线l1:y1=x+m与直线l2:y2=nx+3相交于点C(1,2).
(1)求m,n的值;
(2)在如图所示的直角坐标系中画出直线l1和直线l2;
(3)求不等式nx+3>x+m的解集.
16.(10分)某市端午节期间,甲、乙两队举行了赛龙舟比赛,两队在比赛时的路程s(米)与时间t(分)之间的图像如图所示,请你根据图像,回答下列问题:
(1)这次龙舟赛的全程是多少米 哪队先到达终点
(2)求甲队与乙队相遇时甲队、乙队的速度.
17.(12分)如图,一次函数y=kx+b与y=-2x+3的图像相交于点P,且y=kx+b的图像与x轴相交于点A,交y轴于点B.
(1)求k,b的值;
(2)求点P的坐标;
(3)若x=a是垂直于x轴的直线,交直线y=kx+b于点M,交直线y=-2x+3于点N,且MN的长度等于3,求a的值.
18.(12分)如图,直线y=x+4与x轴、y轴分别交于点A和点B.
(1)求点A,B的坐标;
(2)过点B作直线与x轴交于点P,若△ABP的面积为8,试求点P的坐标;
(3)M是OB上的一点,若将△ABM沿AM折叠,点B恰好落在x轴上的点B1处,求出点M的坐标;
(4)点C在y轴上,连接AC,若△ABC是以AB为腰的等腰三角形,请直接写出点C的坐标.
答案
1.B ①②是一次函数.故选B.
2.D ∵一次函数y=kx+3(k≠0)的函数值y随x的增大而增大,∴k>0.∵该函数图像过点(0,3),∴该函数的图像经过第一、二、三象限,不经过第四象限.故选D.
3.C 因为一次函数y=-x+b中,k=-1<0,b>0,所以一次函数的图像经过第一、二、四象限.故选C.
4.C 将(-2,0),(0,1)代入y=kx+b,得
解得
所以y=x+1.
将A(3,m)代入,得+1=m.
所以m=.故选C.
5.A 把A(m,3)代入y=2x,得m=,所以点A的坐标为.根据图像可以得出不等式2x
因为长方形的周长为20,所以|x|+|y|=10,
即x+y=10.
所以该直线的函数表达式是y=-x+10.
故选B.
7.C 设当x>2时,y与x之间的函数表达式为y=kx+b,则有
解得
所以 y=54x+72.
当x=8时,y=54×8+72=504.
8.> 因为y=kx+b中k<0,所以函数y随x的增大而减小.因为A(-1,y1),B(3,y2)是直线y=kx+b(k<0)上的两点,且-1<3,所以y1>y2.所以y1-y2>0.
9.- 根据题意,将直线y=kx-2先向左平移3个单位长度,再向上平移2个单位长度,得到直线y=kx+3k.因为其正好经过点(2,-4),所以2k+3k=-4.所以k=-.
故答案为-.
10.0 ∵y与x+1成正比,∴设y=k(x+1).∵x=1时,y=2,∴2=k×2,即k=1,∴y=x+1.则当x=-1时,y=-1+1=0.
11.(-2,3) ∵直线y=k1x+b1与直线y=k2x+b2的交点坐标为(2,-3),∴-3=2k1+b1,-3=2k2+b2,∴-b1=2k1+3,-b2=2k2+3,∴直线y=k1x-b1=k1(x+2)+3,直线y=k2x-b2=k2(x+2)+3,∴直线y=k1x-b1与直线y=k2x-b2都经过点(-2,3),∴直线y=k1x-b1与直线y=k2x-b2的交点坐标为(-2,3).
12.k<1 ∵直线y=(2-2k)x+k-3经过第一、三、四象限,∴解得k<1.
13.(2,2)或(-2,0)或(-6,-2)
设点P(m,n)到x轴或y轴的距离为2,则|m|=2或|n|=2,所以m=±2或n=±2.
当m=2时,n=2,此时点P的坐标为(2,2);
当m=-2时,n=0,此时点P的坐标为(-2,0);
当n=2时,m=2,此时点P的坐标为(2,2);
当n=-2时,m=-6,此时点P的坐标为(-6,-2).
故答案为(2,2)或(-2,0)或(-6,-2).
14.(23,8) 由题意可知点A1的纵坐标为1,点A2的纵坐标为2,点A3的纵坐标为4,点A4的纵坐标为8,…
∵点A1和点C1,点A2和点C2,点A3和点C3,点A4和点C4的纵坐标相同,
∴点C1,C2,C3,C4的纵坐标分别为1,2,4,8,
∴根据图像得出C1(2,1),C2(5,2),C3(11,4),
∴直线C1C2的表达式为y=x+.
∵点A4的纵坐标为8,
∴点C4的纵坐标为8.
把y=8代入y=x+,解得x=23,
∴点C4的坐标是(23,8).
15.解:(1)把C(1,2)代入y1=x+m,得1+m=2,解得m=1;
把C(1,2)代入y2=nx+3,得n+3=2,
解得n=-1.
(2)略.
(3)不等式nx+3>x+m的解集为x<1.
16.解:(1)由函数图像可得,这次龙舟赛的全程是1000米,乙队先到达终点.
(2)由图像可得,甲队与乙队相遇时,甲的速度是1000÷4=250(米/分),
乙的速度是(1000-400)÷(3.8-2.2)=600÷1.6=375(米/分),
即甲队与乙队相遇时甲队、乙队的速度分别为250米/分、375米/分.
17.解:(1)由图像可知,一次函数y=kx+b的图像经过点A(1,0),B(0,-3).
把点A,B的坐标代入,得
解得
即k=3,b=-3.
(2)由(1)得一次函数y=kx+b的表达式为y=3x-3,
则有
解得
∴点P的坐标为,.
(3)∵x=a是垂直于x轴的直线,交直线y=kx+b于点M,交直线y=-2x+3于点N,
∴M(a,3a-3),N(a,-2a+3).
∵MN的长度等于3,
∴|3a-3-(-2a+3)|=3,
即|5a-6|=3,
解得a=或a=.
18.解:(1)对于y=x+4,
令y=0,即y=x+4=0,
解得x=-3.
令x=0,则y=4,
故点A,B的坐标分别为(-3,0),(0,4).
(2)设点P(x,0),
则△ABP的面积=×OB×AP=×4×|x+3|=8,
解得x=1或x=-7,
故点P的坐标为(1,0)或(-7,0).
(3)由点A,B的坐标知,OA=3,OB=4,
则AB==5=AB1,
故点B1的坐标为(2,0).
设点M的坐标为(0,m),
由题意得MB=MB1,
即m2+4=(4-m)2,
解得m=1.5,
故点M的坐标为(0,1.5).
(4)设点C(0,t),
则AB=5,AC=.
当AB=BC时,则5=|t-4|,
解得t=9或t=-1,
当AB=AC时,即25=9+t2,
解得t=4(舍去)或t=-4,
故点C的坐标为(0,9)或(0,-1)或(0,-4).
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
