13.4 课题学习 最短路径问题 课件(共38张PPT)
文档属性
| 名称 | 13.4 课题学习 最短路径问题 课件(共38张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-15 15:05:27 | ||
图片预览










文档简介
(共38张PPT)
13.4课题学习 最短路径问题
人教版八年级上册
知识回顾
1.等边三角形的性质有哪些?
2.等边三角形的判断有哪些?
①三边相等的三角形是等边三角形;
②三个角都相等的三角形是等边三角形;
③有一个角是60°的等腰三角形是等边三角形.
①等边三角形的三条边都相等;
②等边三角形的三个角都相等,且每个角都是60°;
③等边三角形每条边上的高、中线和每个角的平分线都重合,有3条对称轴
知识回顾
含30°角的直角三角形的性质:
在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半
含30°角的直角三角形的判定:
直角三角形中的一条直角边等于斜边的一半,那么这条直角边所对的角等于30°.
教学目标
1.利用轴对称、平移等变化解决简单的最短路径问题.
2.体会图形的变化在解决最值问题中的作用,感受由实际问题
转化为数学问题的思想.
新知导入
答:(3)最短,因为两点之间,线段最短.
2.如图,点A是直线l外一点,点A与该直线l上各点连接的所有线段中,哪条最短?为什么?
答:AC最短,因为垂线段最短.
1.如图,连接A、B两点的所有线中,哪条最短?为什么?
l
A
C
B
D
新知讲解
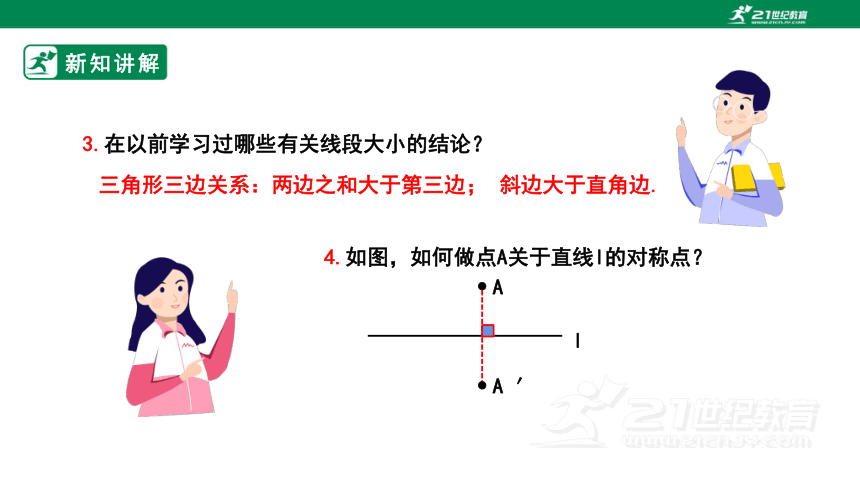
3.在以前学习过哪些有关线段大小的结论?
三角形三边关系:两边之和大于第三边;
斜边大于直角边.
4.如图,如何做点A关于直线l的对称点?
A
l
A ′
新知导入
相传古希腊亚历山大城里有一位久负盛名的学者,名叫海伦.有一天,一位将军专程拜访海伦,请教一个百思不得其解的问题:将军每天从军营A出发,先到河边饮马,然后再去河岸同侧的B地开会,应该怎样走才能使路程最短?从此这个被称为“将军饮马”的问题广泛流传.
l
B
A
利用对称知识解决最短路径问题
知识点 1
新知探究
这是个实际问题,我们需要先建立数学模型,就是将实际问题里的军营A、会议地点B,抽象为A、B两点,将河流抽象为直线l。问题“到河边的什么地方饮马,可使所走的路径最短?”,转换为到直线l上一点C,使AC+CB最短,求点C的位置。
C
A
B
l
数学问题
实际上,这个问题分为2种情况
新知探究
现在假设点A,B分别是直线l异侧的两个点,如何在l上找到一个点,使得这个点到点A,点B的距离的和最短?
(根据“两点之间,线段最短”,可知这个交点即为所求.)
解:连接AB,与直线 l 相交于一点C.
问题1:
A
l
B
C
新知探究
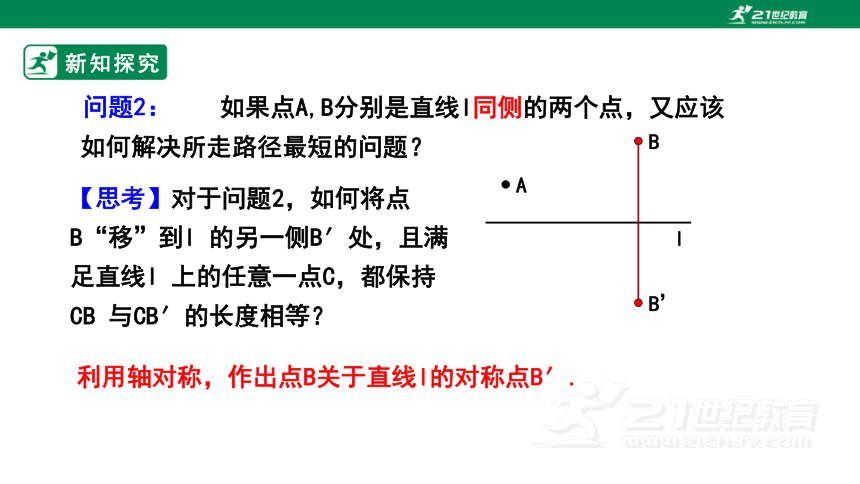
如果点A,B分别是直线l同侧的两个点,又应该如何解决所走路径最短的问题?
【思考】对于问题2,如何将点B“移”到l 的另一侧B′处,且满足直线l 上的任意一点C,都保持CB 与CB′的长度相等?
A
B
l
利用轴对称,作出点B关于直线l的对称点B′.
问题2:
B’
新知探究
如图,作出点B关于直线l的对称点B′,利用轴对称的性质可知:对于直线l上的任意一点C均满足BC=B′C.此时,问题转化为:当点C在直线l的什么位置时,AB+B′C的值最小?
B′
容易得出:连接AB′交直线l于点C,则点C即为所求.
A
B
l
C
新知探究
作法:
(1)作点B 关于直线l 的对称点B′;
(2)连接AB′,与直线l 相交于点C.
此时,AC+BC最小
则点C 即为所求.
A
B
l
B ′
C
探究新知
你能用所学的知识证明AC +BC最短吗?
证明:如图,在直线l 上任取一点C′(与点C 不重合),连接AC′,BC′,B′C′.由轴对称的性质知,
BC =B′C,BC′=B′C′.
∴AC +BC= AC +B′C = AB′,
∴ AC′+BC′= AC′+B′C′.
在△AB′C′中,AB′<AC′+B′C′,
∴ AC +BC<AC′+BC′.
即 AC +BC 最短.
问题3:
A
B
l
B ′
C
C ′
新知典例
例1.如图,牧童在A处放牛,其家在B处,A,B到河岸的距离分别为AC=400米,BD=200米,CD=800米,牧童从A处把牛牵到河边饮水后回家,问在何处饮水能使所走的总路程最短?
解:作点B关于河岸的对称点B′,连接AB′交CD于点P,.
由轴对称的性质可知:PB=PB′,DB′=DB.
∴PA+PB=AP+PB′.
由两点之间线段最短可知;当点A、P、B′在一条直线上时,PA+PB最短.
B′
P
课堂练习
1. 如图,A、B是两个蓄水池,都在河流a的同侧,为了方便灌溉作物,要在河边建一个抽水站,将河水送到A、B两地,问该站建在河边什么地方,可使所修的渠道最短,试在图中确定该点(保留作图痕迹).
解:如图,P点即为该点.
新知典例
例2 如图,在直角坐标系中,点A,B的坐标分别为(1,5)和(4,0),点C是y轴上的一个动点,且A,B,C三点不在同一条直线上,当△ABC的周长最小时点C的坐标是( )
A.(0,4) B.(0,3)
C.(0,2) D.(0,1)
解析:作B点关于y轴对称点B′,连接AB′,交y轴于点C′,此时△ABC的周长最小,然后依据点A与点B′的坐标可得到BE、AE的长,然后证明△B′CO为等腰直角三角形即可.
B′
C′
E
A
课堂练习
1.如图,等边△ABC,AD是BC边上的高,若AD=4,点M为AB中点,点P是线段AD上的动点,则MP+BP最小值为( )
A.4 B.8
C.3 D.5.5
A
P
课堂小结
新知探究
如图,A和B两地在一条河的两岸,现要在河上造一座桥MN.桥造在何处可使从A到B的路径AMNB最短(假定河的两岸是平行的直线,桥要与河垂直)?
A
B
N
M
利用平移知识解决造桥选址问题
知识点 2
B
A
●
●
N
M
N
N
M
M
新知探究
类比问题1,
现在假设点A,B分别是直线l异侧的两个点,如何在l上找到一个点,使得这个点到点A,点B的距离的和最短?
(根据“两点之间,线段最短”,可知这个交点即为所求.)
解:连接AB,与直线 l 相交于一点C.
问题1:
A
l
B
C
新知探究
提出问题
问题2: 问题1与建桥问题有没有相似处?
答:他们起点和重点都在河流的两侧
A
l
B
C
B
A
问题3: 问题1与建桥问题不同之处在哪里?
答:问题1中的河流看作了一条直线,
而建桥问题中的河流是有宽度的。
想法: 如果建桥问题能变成问题1就好了
新知探究
A
l
B
C
实施猜想
1、将原本看作一条直线的河流,变成实际有宽度的河流
2、将原本最短路径上的点C,随直线l一起移动得到点C’
C’
3、连接CC’,河流变宽了,A、B间的距离也增加了,将点B移动与河流同宽的距离到B’
4、在CC’的位置建桥,此时AC+CC’+C’B’是A到B’的最短路程吗?
B’
新知探究
例2 如图,从A地到B地要经过一条小河(河的两岸平行),现要在河上建一座桥(桥垂直于河的两岸),应如何选择桥的位置才能使从A地到B地的路程最短?
A
B
新知探究
解:(1)如图,过点A作AC垂直于河岸,交EF、GH分别于D、C两点,且使得AA’的长等于河宽CD;
分析:这一步就相当于,把点A下移到了A’的位置,也就将河岸EF与GH重合成一条直线GH。使题目变成了“问题1”的模式。
(2)连接A’B,与河岸GH相交于点N,且过点N作MN⊥EF于点M,则MN即为所建桥的位置.
F
H
E
G
A
B
M
N
C
A’
D
分析:无论桥梁的位置在哪里,只要垂直于河流两岸,长度都是一样的,所以能够A到桥再到B距离的,就只有A到B,由于A’B就是最短路径,那么非桥长部分如果等于A’B,总路程就是最短的,所以作图的目的就是让AM等于了A’N,这样AM+BN=A’B,此时就是最短路径。
新知探究
B
A
A1
M
N
如图,平移A到A1,使AA1等于河宽,连接A1B交河岸于N作桥MN,此时路径AM+MN+BN最短.
理由:另任作桥M1N1,连接AM1,BN1,A1N1.
N1
M1
由平移性质可知,AM=A1N,AA1=MN=M1N1,AM1=A1N1.
AM+MN+BN转化为AA1+A1B,而AM1 +M1N1+BN1转化为AA1+A1N1+BN1.
在△A1N1B中,因为A1N1+BN1>A1B.
因此AM1 +M1N1+BN1 > AM+MN+BN.
所以,此作图法选址建桥后的路径就是最短路径
验证作法
课堂练习
2.如图所示,在一条河的两岸有两个村庄,现要在河上建一座小桥,桥的方向与河流垂直,设河的宽度不变,试问:桥架在何处,才能使从A到B的距离最短?
解:如图,作BB'垂直于河岸GH,使BB′等于河宽,
连接AB′,与河岸EF相交于P,作PD⊥GH,
则PD∥BB′且PD=BB′,
于是PDBB′为平行四边形,故PB′=BD.
根据“两点之间线段最短”,AB′最短,即AP+BD最短.
课堂小结
解决最短路径问题的方法
在解决最短路径问题时,我们通常利用轴对称、平移等变换把未知问题转化为已解决的问题,从而作出最短路径的选择.
新知典例
例3 牧马人从A地出发,先到草地边某一处牧马,再到河边饮马,然后回到B处,请画出最短路径.
A
B
P
Q
.
.
.
.
课堂练习
3.某中学八(2)班举行文艺晚会,桌子按如图所示摆成两直排(图中的AO,BO),AO桌面上摆满了桔子,BO桌面上摆满了糖果,站在C处的学生小明先拿桔子再拿糖果,然后回到D处座位上.请你帮助他设计一条行走路线,使其所走的总路程最短.
【分析】作点C关于直线AO的对称点C′,点D关于直线OB的对称点D′,连接C′D′交AO于M,交OB于N,则路线CM﹣MN﹣ND即为所求.
解:如图所示,小明所走的行走路线为:CM﹣MN﹣ND,所走的总路程最短.
课堂小测
1.在平面直角坐标系中有两点,要在y轴上找一点,使它到A、B两点的距离之和最小,现有如下四种方案,其中正确的是( )
A.
B.
C.
D.
D
课堂小测
2.如图,∠AOB=30°,∠AOB内有一定点P,且OP=10.在OA上有一点Q,OB上有一点R.若△PQR周长最小,则最小周长是( )
A.10 B.15 C.20 D.30
A
课堂小测
3.如图,P是∠AOB内一点,分别在OA、OB边上作点C、D,使得△PCD的周长最小.
课堂小测
4.在射线OM、ON分别找两点P、Q,使得四边形PQBA的周长最短.
课堂小测
5.如图,四边形ABCD中,∠C=50°,∠B=∠D=90°,E、F分别是BC、DC上的点,当△AEF的周长最小时,∠EAF的度数为( )
A.50° B.60° C.70° D.80°
解:作A关于BC和CD的对称点A′,A″,连接A′A″,交BC于E,交CD于F,则A′A″即为△AEF的周长最小值.作DA延长线AH,
∵∠C=50°,
∴∠DAB=130°,
∴∠HAA′=50°,
∴∠AA′E+∠A″=∠HAA′=50°,
∵∠EA′A=∠EAA′,∠FAD=∠A″,
∴∠EAA′+∠A″AF=50°,
∴∠EAF=130°﹣50°=80°,
D
课堂总结
原理
线段公理和垂线段最短
最短路径问题
解题方法
造桥选址问题
关键是将固定线段“桥”平移
最短路径问题
轴对称知识+线段公理
解题方法
作业布置
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
13.4课题学习 最短路径问题
人教版八年级上册
知识回顾
1.等边三角形的性质有哪些?
2.等边三角形的判断有哪些?
①三边相等的三角形是等边三角形;
②三个角都相等的三角形是等边三角形;
③有一个角是60°的等腰三角形是等边三角形.
①等边三角形的三条边都相等;
②等边三角形的三个角都相等,且每个角都是60°;
③等边三角形每条边上的高、中线和每个角的平分线都重合,有3条对称轴
知识回顾
含30°角的直角三角形的性质:
在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半
含30°角的直角三角形的判定:
直角三角形中的一条直角边等于斜边的一半,那么这条直角边所对的角等于30°.
教学目标
1.利用轴对称、平移等变化解决简单的最短路径问题.
2.体会图形的变化在解决最值问题中的作用,感受由实际问题
转化为数学问题的思想.
新知导入
答:(3)最短,因为两点之间,线段最短.
2.如图,点A是直线l外一点,点A与该直线l上各点连接的所有线段中,哪条最短?为什么?
答:AC最短,因为垂线段最短.
1.如图,连接A、B两点的所有线中,哪条最短?为什么?
l
A
C
B
D
新知讲解
3.在以前学习过哪些有关线段大小的结论?
三角形三边关系:两边之和大于第三边;
斜边大于直角边.
4.如图,如何做点A关于直线l的对称点?
A
l
A ′
新知导入
相传古希腊亚历山大城里有一位久负盛名的学者,名叫海伦.有一天,一位将军专程拜访海伦,请教一个百思不得其解的问题:将军每天从军营A出发,先到河边饮马,然后再去河岸同侧的B地开会,应该怎样走才能使路程最短?从此这个被称为“将军饮马”的问题广泛流传.
l
B
A
利用对称知识解决最短路径问题
知识点 1
新知探究
这是个实际问题,我们需要先建立数学模型,就是将实际问题里的军营A、会议地点B,抽象为A、B两点,将河流抽象为直线l。问题“到河边的什么地方饮马,可使所走的路径最短?”,转换为到直线l上一点C,使AC+CB最短,求点C的位置。
C
A
B
l
数学问题
实际上,这个问题分为2种情况
新知探究
现在假设点A,B分别是直线l异侧的两个点,如何在l上找到一个点,使得这个点到点A,点B的距离的和最短?
(根据“两点之间,线段最短”,可知这个交点即为所求.)
解:连接AB,与直线 l 相交于一点C.
问题1:
A
l
B
C
新知探究
如果点A,B分别是直线l同侧的两个点,又应该如何解决所走路径最短的问题?
【思考】对于问题2,如何将点B“移”到l 的另一侧B′处,且满足直线l 上的任意一点C,都保持CB 与CB′的长度相等?
A
B
l
利用轴对称,作出点B关于直线l的对称点B′.
问题2:
B’
新知探究
如图,作出点B关于直线l的对称点B′,利用轴对称的性质可知:对于直线l上的任意一点C均满足BC=B′C.此时,问题转化为:当点C在直线l的什么位置时,AB+B′C的值最小?
B′
容易得出:连接AB′交直线l于点C,则点C即为所求.
A
B
l
C
新知探究
作法:
(1)作点B 关于直线l 的对称点B′;
(2)连接AB′,与直线l 相交于点C.
此时,AC+BC最小
则点C 即为所求.
A
B
l
B ′
C
探究新知
你能用所学的知识证明AC +BC最短吗?
证明:如图,在直线l 上任取一点C′(与点C 不重合),连接AC′,BC′,B′C′.由轴对称的性质知,
BC =B′C,BC′=B′C′.
∴AC +BC= AC +B′C = AB′,
∴ AC′+BC′= AC′+B′C′.
在△AB′C′中,AB′<AC′+B′C′,
∴ AC +BC<AC′+BC′.
即 AC +BC 最短.
问题3:
A
B
l
B ′
C
C ′
新知典例
例1.如图,牧童在A处放牛,其家在B处,A,B到河岸的距离分别为AC=400米,BD=200米,CD=800米,牧童从A处把牛牵到河边饮水后回家,问在何处饮水能使所走的总路程最短?
解:作点B关于河岸的对称点B′,连接AB′交CD于点P,.
由轴对称的性质可知:PB=PB′,DB′=DB.
∴PA+PB=AP+PB′.
由两点之间线段最短可知;当点A、P、B′在一条直线上时,PA+PB最短.
B′
P
课堂练习
1. 如图,A、B是两个蓄水池,都在河流a的同侧,为了方便灌溉作物,要在河边建一个抽水站,将河水送到A、B两地,问该站建在河边什么地方,可使所修的渠道最短,试在图中确定该点(保留作图痕迹).
解:如图,P点即为该点.
新知典例
例2 如图,在直角坐标系中,点A,B的坐标分别为(1,5)和(4,0),点C是y轴上的一个动点,且A,B,C三点不在同一条直线上,当△ABC的周长最小时点C的坐标是( )
A.(0,4) B.(0,3)
C.(0,2) D.(0,1)
解析:作B点关于y轴对称点B′,连接AB′,交y轴于点C′,此时△ABC的周长最小,然后依据点A与点B′的坐标可得到BE、AE的长,然后证明△B′CO为等腰直角三角形即可.
B′
C′
E
A
课堂练习
1.如图,等边△ABC,AD是BC边上的高,若AD=4,点M为AB中点,点P是线段AD上的动点,则MP+BP最小值为( )
A.4 B.8
C.3 D.5.5
A
P
课堂小结
新知探究
如图,A和B两地在一条河的两岸,现要在河上造一座桥MN.桥造在何处可使从A到B的路径AMNB最短(假定河的两岸是平行的直线,桥要与河垂直)?
A
B
N
M
利用平移知识解决造桥选址问题
知识点 2
B
A
●
●
N
M
N
N
M
M
新知探究
类比问题1,
现在假设点A,B分别是直线l异侧的两个点,如何在l上找到一个点,使得这个点到点A,点B的距离的和最短?
(根据“两点之间,线段最短”,可知这个交点即为所求.)
解:连接AB,与直线 l 相交于一点C.
问题1:
A
l
B
C
新知探究
提出问题
问题2: 问题1与建桥问题有没有相似处?
答:他们起点和重点都在河流的两侧
A
l
B
C
B
A
问题3: 问题1与建桥问题不同之处在哪里?
答:问题1中的河流看作了一条直线,
而建桥问题中的河流是有宽度的。
想法: 如果建桥问题能变成问题1就好了
新知探究
A
l
B
C
实施猜想
1、将原本看作一条直线的河流,变成实际有宽度的河流
2、将原本最短路径上的点C,随直线l一起移动得到点C’
C’
3、连接CC’,河流变宽了,A、B间的距离也增加了,将点B移动与河流同宽的距离到B’
4、在CC’的位置建桥,此时AC+CC’+C’B’是A到B’的最短路程吗?
B’
新知探究
例2 如图,从A地到B地要经过一条小河(河的两岸平行),现要在河上建一座桥(桥垂直于河的两岸),应如何选择桥的位置才能使从A地到B地的路程最短?
A
B
新知探究
解:(1)如图,过点A作AC垂直于河岸,交EF、GH分别于D、C两点,且使得AA’的长等于河宽CD;
分析:这一步就相当于,把点A下移到了A’的位置,也就将河岸EF与GH重合成一条直线GH。使题目变成了“问题1”的模式。
(2)连接A’B,与河岸GH相交于点N,且过点N作MN⊥EF于点M,则MN即为所建桥的位置.
F
H
E
G
A
B
M
N
C
A’
D
分析:无论桥梁的位置在哪里,只要垂直于河流两岸,长度都是一样的,所以能够A到桥再到B距离的,就只有A到B,由于A’B就是最短路径,那么非桥长部分如果等于A’B,总路程就是最短的,所以作图的目的就是让AM等于了A’N,这样AM+BN=A’B,此时就是最短路径。
新知探究
B
A
A1
M
N
如图,平移A到A1,使AA1等于河宽,连接A1B交河岸于N作桥MN,此时路径AM+MN+BN最短.
理由:另任作桥M1N1,连接AM1,BN1,A1N1.
N1
M1
由平移性质可知,AM=A1N,AA1=MN=M1N1,AM1=A1N1.
AM+MN+BN转化为AA1+A1B,而AM1 +M1N1+BN1转化为AA1+A1N1+BN1.
在△A1N1B中,因为A1N1+BN1>A1B.
因此AM1 +M1N1+BN1 > AM+MN+BN.
所以,此作图法选址建桥后的路径就是最短路径
验证作法
课堂练习
2.如图所示,在一条河的两岸有两个村庄,现要在河上建一座小桥,桥的方向与河流垂直,设河的宽度不变,试问:桥架在何处,才能使从A到B的距离最短?
解:如图,作BB'垂直于河岸GH,使BB′等于河宽,
连接AB′,与河岸EF相交于P,作PD⊥GH,
则PD∥BB′且PD=BB′,
于是PDBB′为平行四边形,故PB′=BD.
根据“两点之间线段最短”,AB′最短,即AP+BD最短.
课堂小结
解决最短路径问题的方法
在解决最短路径问题时,我们通常利用轴对称、平移等变换把未知问题转化为已解决的问题,从而作出最短路径的选择.
新知典例
例3 牧马人从A地出发,先到草地边某一处牧马,再到河边饮马,然后回到B处,请画出最短路径.
A
B
P
Q
.
.
.
.
课堂练习
3.某中学八(2)班举行文艺晚会,桌子按如图所示摆成两直排(图中的AO,BO),AO桌面上摆满了桔子,BO桌面上摆满了糖果,站在C处的学生小明先拿桔子再拿糖果,然后回到D处座位上.请你帮助他设计一条行走路线,使其所走的总路程最短.
【分析】作点C关于直线AO的对称点C′,点D关于直线OB的对称点D′,连接C′D′交AO于M,交OB于N,则路线CM﹣MN﹣ND即为所求.
解:如图所示,小明所走的行走路线为:CM﹣MN﹣ND,所走的总路程最短.
课堂小测
1.在平面直角坐标系中有两点,要在y轴上找一点,使它到A、B两点的距离之和最小,现有如下四种方案,其中正确的是( )
A.
B.
C.
D.
D
课堂小测
2.如图,∠AOB=30°,∠AOB内有一定点P,且OP=10.在OA上有一点Q,OB上有一点R.若△PQR周长最小,则最小周长是( )
A.10 B.15 C.20 D.30
A
课堂小测
3.如图,P是∠AOB内一点,分别在OA、OB边上作点C、D,使得△PCD的周长最小.
课堂小测
4.在射线OM、ON分别找两点P、Q,使得四边形PQBA的周长最短.
课堂小测
5.如图,四边形ABCD中,∠C=50°,∠B=∠D=90°,E、F分别是BC、DC上的点,当△AEF的周长最小时,∠EAF的度数为( )
A.50° B.60° C.70° D.80°
解:作A关于BC和CD的对称点A′,A″,连接A′A″,交BC于E,交CD于F,则A′A″即为△AEF的周长最小值.作DA延长线AH,
∵∠C=50°,
∴∠DAB=130°,
∴∠HAA′=50°,
∴∠AA′E+∠A″=∠HAA′=50°,
∵∠EA′A=∠EAA′,∠FAD=∠A″,
∴∠EAA′+∠A″AF=50°,
∴∠EAF=130°﹣50°=80°,
D
课堂总结
原理
线段公理和垂线段最短
最短路径问题
解题方法
造桥选址问题
关键是将固定线段“桥”平移
最短路径问题
轴对称知识+线段公理
解题方法
作业布置
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
