1.3.1有理数的加法 课件(共49张PPT)
文档属性
| 名称 | 1.3.1有理数的加法 课件(共49张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 514.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-22 09:44:13 | ||
图片预览









文档简介
(共49张PPT)
1.3 有理数的加减法
1.3.1 有理数的加法
第1课时 有理数的加法
R·七年级上册
学习目标:
1.能叙述并理解有理数加法法则.
2.会用有理数加法法则正确进行有理数加法运算.
小学学过的加法类型是正数与正数相加、正数与0相加.引入负数后,加法的类型还有哪几种呢?
推进新课
思考
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
正数 0 负数
正数
0
负数
第一个加数
第二个加数
正数+正数
0+正数
负数+正数
0+0
负数+0
0+负数
负数+负数
正数+0
正数+负数
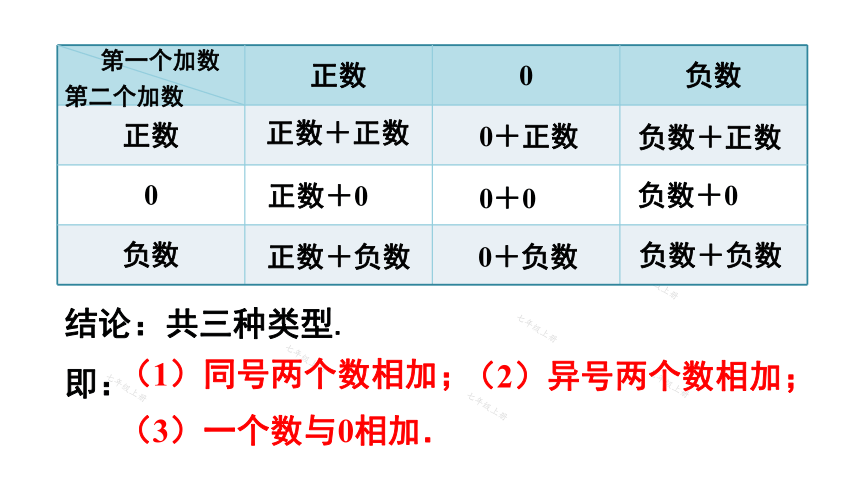
结论:共三种类型.
即:
(1)同号两个数相加;
(2)异号两个数相加;
(3)一个数与0相加.
探究有理数加法的法则
知识点1
一个物体作左右方向的运动,我们规定向左为负,向右为正.比如:向右运动5 m记作5 m,向左运动5 m记作-5 m.
观察探究
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
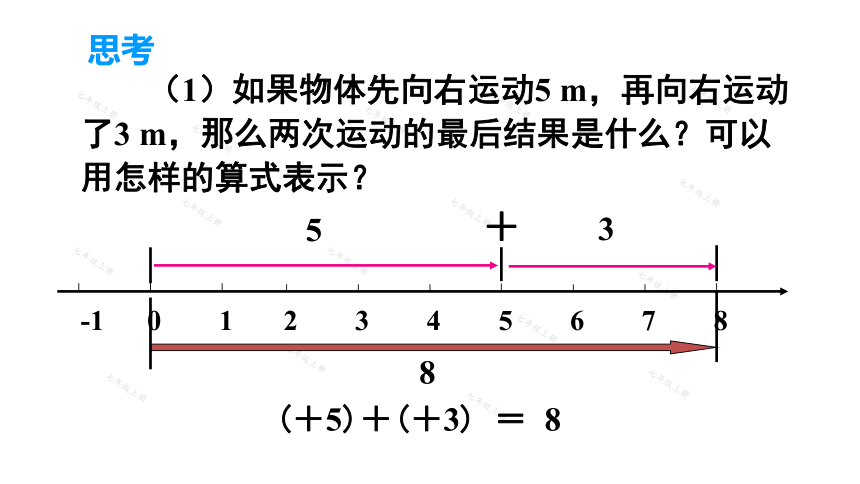
(1)如果物体先向右运动5 m,再向右运动了3 m,那么两次运动的最后结果是什么?可以用怎样的算式表示?
(+5)+(+3) = 8
-1 0 1 2 3 4 5 6 7 8
5
3
+
8
思考
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
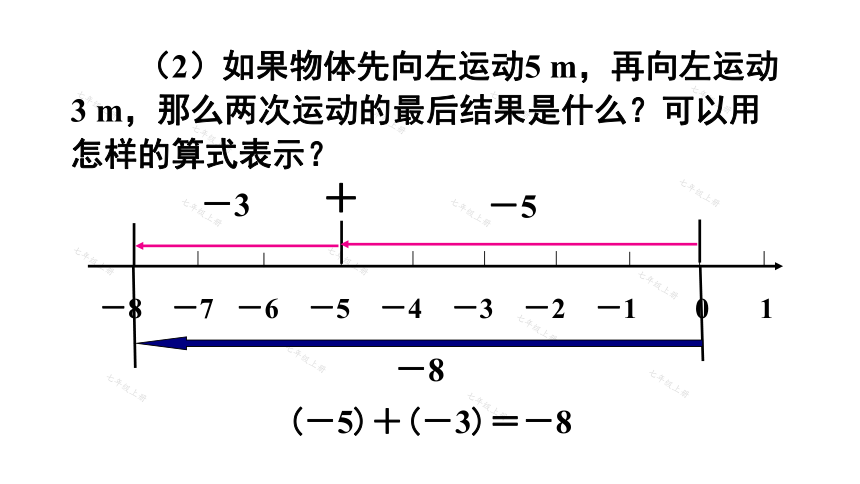
(2)如果物体先向左运动5 m,再向左运动3 m,那么两次运动的最后结果是什么?可以用怎样的算式表示?
-3
-5
(-5)+(-3)=-8
+
-8
-8 -7 -6 -5 -4 -3 -2 -1 0 1
根据以上两个算式能否尝试总结同号两数相加的法则?
(+5)+(+3)= 8
(-5)+(-3)=-8
归纳法则
注意关注加数的符号和绝对值
同号两数相加,取相同符号,并把绝对值相加.
结论:
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
利用数轴,求以下物体两次运动的结果,并用算式表示:
(1)先向左运动3 m,再向右运动5 m,
物体从起点向____运动了____m,____________;
(2)先向右运动了3 m,再向左运动了5 m,
物体从起点向____运动了____m,____________;
(3)先向左运动了5 m,再向右运动了5 m,
物体从起点运动了____m,_____________.
0
右
左
2
2
(-3)+5=2
3+(-5)=-2
(-5)+5= 0
探究
根据以上三个算式能否尝试总结异号两数相加的法则?
注意关注加数的符号和绝对值
绝对值不相等的异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值,互为相反数的两个数相加得0 .
结论:
(-3)+5= 2
3+(-5)=-2
(-5)+5= 0
归纳法则
如果物体第1 s向右(或左)运动5 m,第2 s原地不动,那么2 s后物体从起点向右(或左)运动了5 m.如何用算式表示呢?
直接说出结论
5+0=5. 或 (-5)+0=-5.
结论:
一个数同0相加,仍得这个数.
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
归纳法则
1.同号两数相加,取相同的符号,并把绝对值相加.
2.绝对值不相等的异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值.互为相反数的两个数相加得0.
3.一个数同0相加,仍得这个数.
有理数加法法则:
例 计算:
(1)(-3)+(-9);
(2)(-4.7)+3.9;
(3) 0+(-7);
(4)(-9)+(+9).
有理数加法的运算
知识点2
七年级上册
七年级上册
七年级上册
状成才路
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
解:
(1)(-3)+(-9)=
同号两数相加
-
(3+9)
=-12;
(2)(-4.7)+3.9=
取相同符号
把绝对值相加
(4.7-3.9)
-
=-0.8;
异号两数相加
取绝对值较大加数的符号
用较大的绝对值减较小的绝对值
解:
(3) 0+(-7)=-7;
(4)(-9)+(+9)= 0.
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
有理数加法的运算步骤:
一要辨别加数的类型(同号、异号);
二要确定和的符号;
三要计算绝对值的和(或差).
可要记住哟!
即“一看、二定、三算”.
课堂练习
1.用算式表示下面的结果:
(1)温度由-4 ℃上升7 ℃;
(2)收入7元,又支出5元.
-4+7=3
7-5=2
【课本P18 练习 第1题】
2.口算:
(1)(-4)+(-6); (2) 4+(-6);
(3)(-4)+6; (4)(-4)+4;
(5)(-4)+14; (6)(-14)+4;
(7) 6+(-6); (8) 0+(-6).
-10
-2
2
0
10
-10
0
-6
【课本P18 练习 第2题】
3.计算:
(1)15+(-22); (2)(-13) +(-8);
(3)(-0.9) +1.5; (4)
【课本P19 练习 第3题】
=-7
=-21
=-0.6
【课本P19 练习 第4题】
4. 请你用生活实例解释5+(-3) =2,
(-5)+(-3) =-8的意义.
随堂演练
1.两个有理数的和为负数,则这两个数一定( ).
A.都是负数 B.只有一个负数
C.至少有一个负数 D.无法确定
C
基础巩固
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
2.请你用生活中的例子解释算式(+3)+(-3) = 0;(-1)+(-2) = -3.
综合应用
解:①冬季某天早晨温度为0度,到中午气温上升了3度,再到下午又下降了3度,下午气温为0度;
②取向东为正方向,先向西走了1 km,后又走了2 km,一共向西走了3 km.
3.数a,b表示的点如图所示,则
(1)a + b _____ 0;
(2)a + (-b)_____ 0;
(3)(-a) + b _____ 0;
(4)(-a) + (-b) _____0.
(填“>”“<”或“=”)
拓展延伸
>
<
>
<
课堂小结
1.同号两数相加,取相同的符号,并把绝对值相加.
2.绝对值不相等的异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值,互为相反数的两个数相加得0.
3.一个数同0相加,仍得这个数.
有理数加法法则:
1.3.1 有理数的加法
第2课时 有理数的加法运算律
R·七年级上册
我们以前学过加法交换律、结合律,在有理数的加法中它们还适用吗?
新课导入
学习目标:
1.能叙述有理数加法运算律.
2.会运用加法运算律进行有理数加法简便运算.
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
推进新课
(1)比较以上各组两个算式的结果有什么关系?
每组两个算式有什么特征?
① 30+(-20) (-20)+30
② (-5)+(-13) (-13)+(-5)
③ (-37)+16 16+(-37)
(2)小学学的加法交换律在有理数的加法中还适用吗?
(3)请你再换几个加数,试一试,看一看所得的结果如何?
计算
探究有理数加法的交换律和结合律
知识点1
你能用精炼的语言表述这一结论吗?
你能把该规律用字母表示吗?
有理数加法中,两个数相加,交换加数的位置,和不变.
总结归纳
加法交换律:
两次所得的和相同吗?换几个加数再试一试.
从上述计算中,你能得出什么结论?
计算并观察
[8+ (-5)]+(-4) ,8+[(-5) +(-4)]
有理数的加法中,三个数相加,先把前两个数相加,或者先把后两个数相加,和不变.
加法结合律:
总结归纳
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
例2 计算 16+(-25)+24+(-35).
怎样使计算简化的?根据是什么?
= 16 + 24 +[(-25) +(-35)]
= 40 +(- 60)
= -20.
解: 16+(-25)+24+(-35)
把正数和负数分别相加,从而使计算简化.这样做的依据是加法的交换律和结合律.
有理数加法的交换律和结合律的应用
知识点2
练习:教科书第20页
1.计算:
(1)23 + (-17) + 6 + (-22)
(2)(-2) + 3 + 1 + (-3) + 2 + (-4)
23 +(-17) + 6 +(-22)
= 23 + 6 + [(-17) +(-22)]
= 29 +(-39)
= -10
解:(1)
(-2) +3 + 1 +(-3) + 2+(-4)
= [ (-2) +2 ]+[ 3+(-3) ]+[ 1+(-4)]
= 1 +(-4)
= -3
解:(2)
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
例3 10袋小麦称后记录如图所示(单位:kg)
(1)10袋小麦一共多少kg?
(2)如果每袋小麦以90 kg为标准,10袋小麦总计超过多少千克或不足多少kg?
在计算中我们可以使用哪些运算律?
再计算总计超过多少千克:
905.4-90×10 = 5.4(千克).
解法1: 先计算10袋小麦一共多少千克:
91+91+91.5+89+91.2+91.3+88.7+88.8+91.8+91.1 = 905.4 (千克) .
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
解法2:每袋小麦超过90千克的千克数记作正数,不足的千克数记作负数.10袋小麦对应的数分别为+1,+1,+1.5,-1,+1.2,+1.3,-1.3,-1.2,+1.8,+1.1.
1+1+1.5+(-1)+1.2+1.3+(-1.3)+(-1.2)+1.8+1.1
= [1+(-1)]+[1.2+(-1.2)]+[1.3+(-1.3)]+
(1+1.5+1.8+1.1)
= 5.4.
90×10+5.4 = 905.4.
答:10袋小麦一共905.4千克,总计超过5.4千克.
比较两种解法.解法2中使用了哪些运算律?
解法 2 中运用了加法的交换律和结合律.解法 2 较好,使运算更简便.
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
练习1: 某学习小组五位同学某次数学测试成绩(分)为83、76、94、88、74,该班全体同学测试的平均分为80分,问这五位同学的平均分超出全班平均分多少分?用两种方法解答.
解法一:先计算这5个人的平均分是多少分:
(83+76+94+88+74)÷5 = 83,
再计算超过平均分多少分:
83-80 = 3.
解法二:每个人的分数超过平均分的记为正数,低于平均分的记为负数,则5个人对应的数分别为:+3,-4,+14,+8,-6.
[( +3)+(-4)+(+14)+(+8) +(-6)]÷5 = 3.
答:这五位同学的平均分超出全班平均分3分.
(1)
(2)
2.计算:
练习2 教科书第20页
解:(1)
解:(2)
有理数加法运算常用方法:
(1)正负数归类法;
(2)相反数结合法;
(3)凑整数;
(4)同分母分数结合法.
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
随堂演练
1.(30分) 运用运算律计算恰当的是( )
A. B.
C. D. 以上都不对
基础巩固
A
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
2.有8筐白菜,以每筐25kg为标准,超过的千克数记作正数,不足的千克数记作负数,称后的记录如下:1.5,-3,2,-0.5,1,-2,-2,-2.5.这8筐白菜一共多少千克?
综合应用
解:1.5+(-3)+2+(-0.5)+1+(-2)+(-2)+(-2.5)+25×8=194.5(千克).
答:这8筐白菜一共194.5千克.
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
3. (1)计算下列各式的值.
①(-2)+(-2);
②(-2)+(-2)+(-2);
③(-2)+(-2)+(-2)+(-2);
④(-2)+(-2)+(-2)+(-2)+(-2).
(2)猜想下列各式的值:
(-2)×2;(-2)×3;(-2)×4;(-2)×5.
你能进一步猜出一个负数乘一个正数的法则吗?
拓展延伸
解:(1)①-4;②-6;③-8;④-10.
(2)(-2)×2=-4,(-2)×3=-6,(-2)×4=-8,(-2)×5=-10
负数乘正数的法则:符号取负号,再把两数的绝对值相乘.
课堂小结
有理数加法中,两个数相加,交换加数的位置,和不变.
加法交换律:
有理数的加法中,三个数相加,先把前两个数相加,或者先把后两个数相加,和不变.
加法结合律:
1.3 有理数的加减法
1.3.1 有理数的加法
第1课时 有理数的加法
R·七年级上册
学习目标:
1.能叙述并理解有理数加法法则.
2.会用有理数加法法则正确进行有理数加法运算.
小学学过的加法类型是正数与正数相加、正数与0相加.引入负数后,加法的类型还有哪几种呢?
推进新课
思考
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
正数 0 负数
正数
0
负数
第一个加数
第二个加数
正数+正数
0+正数
负数+正数
0+0
负数+0
0+负数
负数+负数
正数+0
正数+负数
结论:共三种类型.
即:
(1)同号两个数相加;
(2)异号两个数相加;
(3)一个数与0相加.
探究有理数加法的法则
知识点1
一个物体作左右方向的运动,我们规定向左为负,向右为正.比如:向右运动5 m记作5 m,向左运动5 m记作-5 m.
观察探究
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
(1)如果物体先向右运动5 m,再向右运动了3 m,那么两次运动的最后结果是什么?可以用怎样的算式表示?
(+5)+(+3) = 8
-1 0 1 2 3 4 5 6 7 8
5
3
+
8
思考
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
(2)如果物体先向左运动5 m,再向左运动3 m,那么两次运动的最后结果是什么?可以用怎样的算式表示?
-3
-5
(-5)+(-3)=-8
+
-8
-8 -7 -6 -5 -4 -3 -2 -1 0 1
根据以上两个算式能否尝试总结同号两数相加的法则?
(+5)+(+3)= 8
(-5)+(-3)=-8
归纳法则
注意关注加数的符号和绝对值
同号两数相加,取相同符号,并把绝对值相加.
结论:
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
利用数轴,求以下物体两次运动的结果,并用算式表示:
(1)先向左运动3 m,再向右运动5 m,
物体从起点向____运动了____m,____________;
(2)先向右运动了3 m,再向左运动了5 m,
物体从起点向____运动了____m,____________;
(3)先向左运动了5 m,再向右运动了5 m,
物体从起点运动了____m,_____________.
0
右
左
2
2
(-3)+5=2
3+(-5)=-2
(-5)+5= 0
探究
根据以上三个算式能否尝试总结异号两数相加的法则?
注意关注加数的符号和绝对值
绝对值不相等的异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值,互为相反数的两个数相加得0 .
结论:
(-3)+5= 2
3+(-5)=-2
(-5)+5= 0
归纳法则
如果物体第1 s向右(或左)运动5 m,第2 s原地不动,那么2 s后物体从起点向右(或左)运动了5 m.如何用算式表示呢?
直接说出结论
5+0=5. 或 (-5)+0=-5.
结论:
一个数同0相加,仍得这个数.
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
归纳法则
1.同号两数相加,取相同的符号,并把绝对值相加.
2.绝对值不相等的异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值.互为相反数的两个数相加得0.
3.一个数同0相加,仍得这个数.
有理数加法法则:
例 计算:
(1)(-3)+(-9);
(2)(-4.7)+3.9;
(3) 0+(-7);
(4)(-9)+(+9).
有理数加法的运算
知识点2
七年级上册
七年级上册
七年级上册
状成才路
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
解:
(1)(-3)+(-9)=
同号两数相加
-
(3+9)
=-12;
(2)(-4.7)+3.9=
取相同符号
把绝对值相加
(4.7-3.9)
-
=-0.8;
异号两数相加
取绝对值较大加数的符号
用较大的绝对值减较小的绝对值
解:
(3) 0+(-7)=-7;
(4)(-9)+(+9)= 0.
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
有理数加法的运算步骤:
一要辨别加数的类型(同号、异号);
二要确定和的符号;
三要计算绝对值的和(或差).
可要记住哟!
即“一看、二定、三算”.
课堂练习
1.用算式表示下面的结果:
(1)温度由-4 ℃上升7 ℃;
(2)收入7元,又支出5元.
-4+7=3
7-5=2
【课本P18 练习 第1题】
2.口算:
(1)(-4)+(-6); (2) 4+(-6);
(3)(-4)+6; (4)(-4)+4;
(5)(-4)+14; (6)(-14)+4;
(7) 6+(-6); (8) 0+(-6).
-10
-2
2
0
10
-10
0
-6
【课本P18 练习 第2题】
3.计算:
(1)15+(-22); (2)(-13) +(-8);
(3)(-0.9) +1.5; (4)
【课本P19 练习 第3题】
=-7
=-21
=-0.6
【课本P19 练习 第4题】
4. 请你用生活实例解释5+(-3) =2,
(-5)+(-3) =-8的意义.
随堂演练
1.两个有理数的和为负数,则这两个数一定( ).
A.都是负数 B.只有一个负数
C.至少有一个负数 D.无法确定
C
基础巩固
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
2.请你用生活中的例子解释算式(+3)+(-3) = 0;(-1)+(-2) = -3.
综合应用
解:①冬季某天早晨温度为0度,到中午气温上升了3度,再到下午又下降了3度,下午气温为0度;
②取向东为正方向,先向西走了1 km,后又走了2 km,一共向西走了3 km.
3.数a,b表示的点如图所示,则
(1)a + b _____ 0;
(2)a + (-b)_____ 0;
(3)(-a) + b _____ 0;
(4)(-a) + (-b) _____0.
(填“>”“<”或“=”)
拓展延伸
>
<
>
<
课堂小结
1.同号两数相加,取相同的符号,并把绝对值相加.
2.绝对值不相等的异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值,互为相反数的两个数相加得0.
3.一个数同0相加,仍得这个数.
有理数加法法则:
1.3.1 有理数的加法
第2课时 有理数的加法运算律
R·七年级上册
我们以前学过加法交换律、结合律,在有理数的加法中它们还适用吗?
新课导入
学习目标:
1.能叙述有理数加法运算律.
2.会运用加法运算律进行有理数加法简便运算.
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
推进新课
(1)比较以上各组两个算式的结果有什么关系?
每组两个算式有什么特征?
① 30+(-20) (-20)+30
② (-5)+(-13) (-13)+(-5)
③ (-37)+16 16+(-37)
(2)小学学的加法交换律在有理数的加法中还适用吗?
(3)请你再换几个加数,试一试,看一看所得的结果如何?
计算
探究有理数加法的交换律和结合律
知识点1
你能用精炼的语言表述这一结论吗?
你能把该规律用字母表示吗?
有理数加法中,两个数相加,交换加数的位置,和不变.
总结归纳
加法交换律:
两次所得的和相同吗?换几个加数再试一试.
从上述计算中,你能得出什么结论?
计算并观察
[8+ (-5)]+(-4) ,8+[(-5) +(-4)]
有理数的加法中,三个数相加,先把前两个数相加,或者先把后两个数相加,和不变.
加法结合律:
总结归纳
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
例2 计算 16+(-25)+24+(-35).
怎样使计算简化的?根据是什么?
= 16 + 24 +[(-25) +(-35)]
= 40 +(- 60)
= -20.
解: 16+(-25)+24+(-35)
把正数和负数分别相加,从而使计算简化.这样做的依据是加法的交换律和结合律.
有理数加法的交换律和结合律的应用
知识点2
练习:教科书第20页
1.计算:
(1)23 + (-17) + 6 + (-22)
(2)(-2) + 3 + 1 + (-3) + 2 + (-4)
23 +(-17) + 6 +(-22)
= 23 + 6 + [(-17) +(-22)]
= 29 +(-39)
= -10
解:(1)
(-2) +3 + 1 +(-3) + 2+(-4)
= [ (-2) +2 ]+[ 3+(-3) ]+[ 1+(-4)]
= 1 +(-4)
= -3
解:(2)
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
例3 10袋小麦称后记录如图所示(单位:kg)
(1)10袋小麦一共多少kg?
(2)如果每袋小麦以90 kg为标准,10袋小麦总计超过多少千克或不足多少kg?
在计算中我们可以使用哪些运算律?
再计算总计超过多少千克:
905.4-90×10 = 5.4(千克).
解法1: 先计算10袋小麦一共多少千克:
91+91+91.5+89+91.2+91.3+88.7+88.8+91.8+91.1 = 905.4 (千克) .
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
解法2:每袋小麦超过90千克的千克数记作正数,不足的千克数记作负数.10袋小麦对应的数分别为+1,+1,+1.5,-1,+1.2,+1.3,-1.3,-1.2,+1.8,+1.1.
1+1+1.5+(-1)+1.2+1.3+(-1.3)+(-1.2)+1.8+1.1
= [1+(-1)]+[1.2+(-1.2)]+[1.3+(-1.3)]+
(1+1.5+1.8+1.1)
= 5.4.
90×10+5.4 = 905.4.
答:10袋小麦一共905.4千克,总计超过5.4千克.
比较两种解法.解法2中使用了哪些运算律?
解法 2 中运用了加法的交换律和结合律.解法 2 较好,使运算更简便.
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
练习1: 某学习小组五位同学某次数学测试成绩(分)为83、76、94、88、74,该班全体同学测试的平均分为80分,问这五位同学的平均分超出全班平均分多少分?用两种方法解答.
解法一:先计算这5个人的平均分是多少分:
(83+76+94+88+74)÷5 = 83,
再计算超过平均分多少分:
83-80 = 3.
解法二:每个人的分数超过平均分的记为正数,低于平均分的记为负数,则5个人对应的数分别为:+3,-4,+14,+8,-6.
[( +3)+(-4)+(+14)+(+8) +(-6)]÷5 = 3.
答:这五位同学的平均分超出全班平均分3分.
(1)
(2)
2.计算:
练习2 教科书第20页
解:(1)
解:(2)
有理数加法运算常用方法:
(1)正负数归类法;
(2)相反数结合法;
(3)凑整数;
(4)同分母分数结合法.
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
随堂演练
1.(30分) 运用运算律计算恰当的是( )
A. B.
C. D. 以上都不对
基础巩固
A
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
2.有8筐白菜,以每筐25kg为标准,超过的千克数记作正数,不足的千克数记作负数,称后的记录如下:1.5,-3,2,-0.5,1,-2,-2,-2.5.这8筐白菜一共多少千克?
综合应用
解:1.5+(-3)+2+(-0.5)+1+(-2)+(-2)+(-2.5)+25×8=194.5(千克).
答:这8筐白菜一共194.5千克.
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
七年级上册
3. (1)计算下列各式的值.
①(-2)+(-2);
②(-2)+(-2)+(-2);
③(-2)+(-2)+(-2)+(-2);
④(-2)+(-2)+(-2)+(-2)+(-2).
(2)猜想下列各式的值:
(-2)×2;(-2)×3;(-2)×4;(-2)×5.
你能进一步猜出一个负数乘一个正数的法则吗?
拓展延伸
解:(1)①-4;②-6;③-8;④-10.
(2)(-2)×2=-4,(-2)×3=-6,(-2)×4=-8,(-2)×5=-10
负数乘正数的法则:符号取负号,再把两数的绝对值相乘.
课堂小结
有理数加法中,两个数相加,交换加数的位置,和不变.
加法交换律:
有理数的加法中,三个数相加,先把前两个数相加,或者先把后两个数相加,和不变.
加法结合律:
