第二十三章 旋转单元同步检测试题(含答案)
文档属性
| 名称 | 第二十三章 旋转单元同步检测试题(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 434.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-06 10:45:04 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
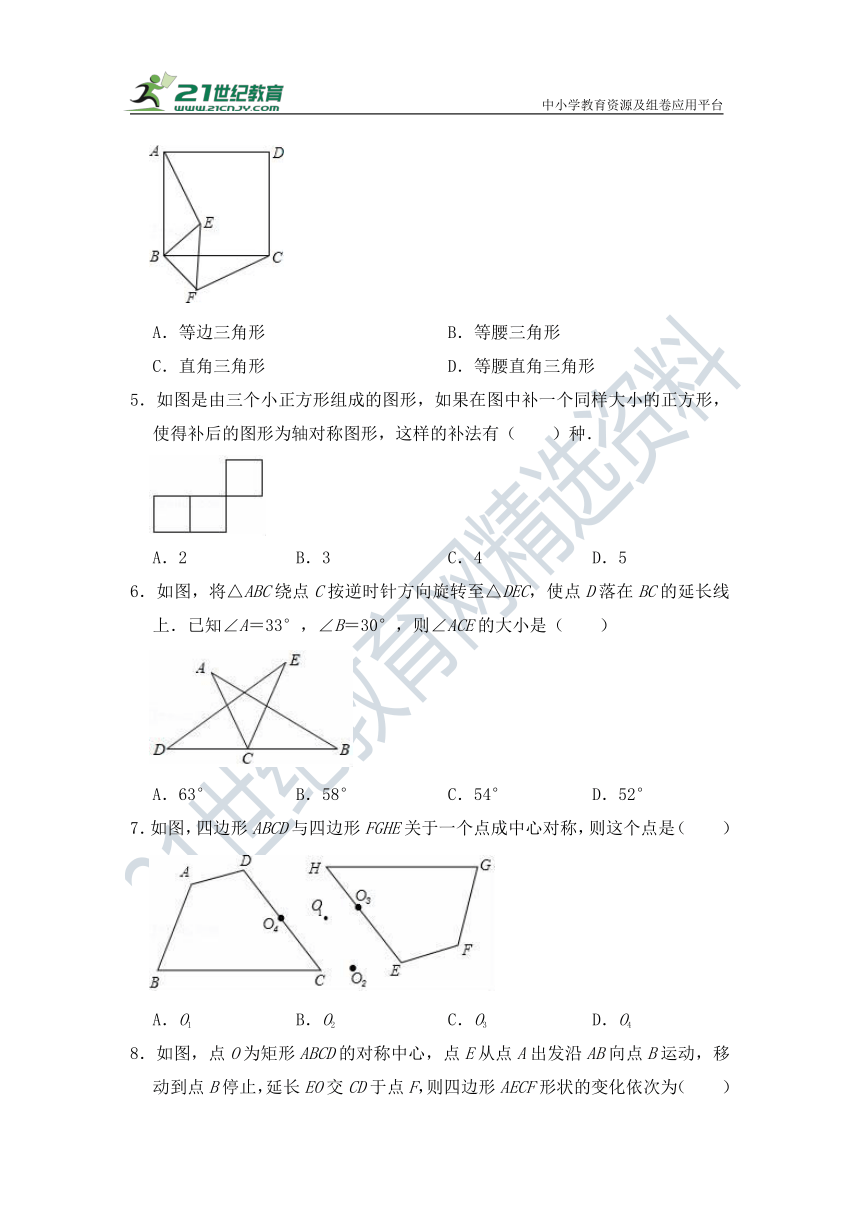
第二十三章 《旋转》单元测试卷
题号 一 二 三 总分
19 20 21 22 23 24
分数
一、选择题(每题3分,共30分)
1.在下列四个图案中既是轴对称图形,又是中心对称图形的是( )
A. B. C. D.
2如图,在Rt△ABC中,∠BAC=90°,将△ABC绕点A顺时针旋转90°后得到△AB′C′(点B的对应点是点B′,点C的对应点是点C′),连接CC′.若∠CC′B′=32°,则∠B的大小是( )
A.32° B.64° C.77° D.87°
3如图,紫荆花图案旋转一定角度后能与自身重合,则旋转的角度可能是( )
A.30° B.60° C.72° D.90°
4如图,在正方形ABCD中有一点E,把△ABE绕点B旋转到△CBF,连接EF,则△EBF的形状是( )
A.等边三角形 B.等腰三角形
C.直角三角形 D.等腰直角三角形
5.如图是由三个小正方形组成的图形,如果在图中补一个同样大小的正方形,使得补后的图形为轴对称图形,这样的补法有( )种.
A.2 B.3 C.4 D.5
6.如图,将△ABC绕点C按逆时针方向旋转至△DEC,使点D落在BC的延长线上.已知∠A=33°,∠B=30°,则∠ACE的大小是( )
A.63° B.58° C.54° D.52°
7.如图,四边形ABCD与四边形FGHE关于一个点成中心对称,则这个点是( )
A.O1 B.O2 C.O3 D.O4
8.如图,点O为矩形ABCD的对称中心,点E从点A出发沿AB向点B运动,移动到点B停止,延长EO交CD于点F,则四边形AECF形状的变化依次为( )
A.平行四边形→正方形→平行四边形→矩形
B.平行四边形→菱形→平行四边形→矩形
C.平行四边形→正方形→菱形→矩形
D.平行四边形→菱形→正方形→矩形
9.如图,△AOB中,∠ABO=90°,点B在x轴上,点A坐标为(2,2),将△AOB绕点O逆时针旋转15°,此时点A的对应点A'的坐标是( )
A.(,) B.(,) C.(,2) D.(1,)
10.下列各组图形中,△A'B'C'与△ABC成中心对称的是( )
A. B.
C. D.
二、填空题(每题3分,共24分)
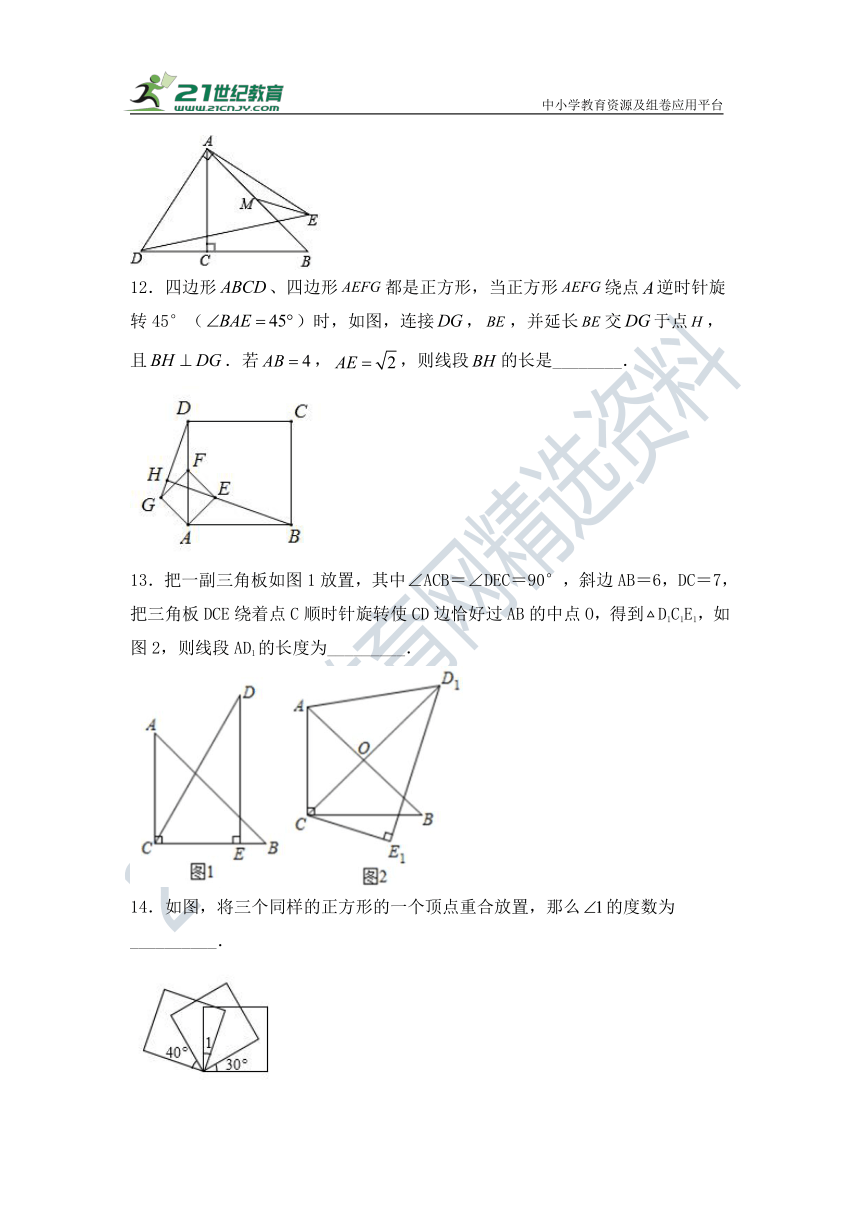
11.如图,等腰直角△ABC中,∠ACB=90°,AC=BC=4,M为AB中点,D是射线BC上一动点,连接AD,将线段AD绕点A逆时针旋转90°得到线段AE,连接ED、ME,则点D在运动过程中ME的最小值为_____.
12.四边形、四边形都是正方形,当正方形绕点逆时针旋转45°()时,如图,连接,,并延长交于点,且.若,,则线段的长是________.
13.把一副三角板如图1放置,其中∠ACB=∠DEC=90°,斜边AB=6,DC=7,把三角板DCE绕着点C顺时针旋转使CD边恰好过AB的中点O,得到D1C1E1,如图2,则线段AD1的长度为_________.
14.如图,将三个同样的正方形的一个顶点重合放置,那么的度数为__________.
15.如图,点P为定角∠AOB的平分线上的一个定点,且∠MPN与∠AOB互补,若∠MPN在绕点P旋转的过程中,其两边分别与OA、OB相交于M、N两点,则以下结论:(1)PM=PN恒成立;(2)OM﹣ON的值不变;(3)△OMN的周长不变;(4)四边形PMON的面积不变,其中正确的序号为_____.
16.如图,将绕点旋转得到,改点的坐标为,则点的坐标为__________.
17.如图,在中,,,.将绕顶点按顺时针方向旋转到处,此时线段与的交点恰好为的中点,则线段__________.
18.如图,在正方形中,,把边绕点逆时针旋转得到线段,连接并延长交于点,连接,则三角形的面积为__________.
三.解答题(共46分,19题6分,20 ---24题8分)
19.如图,△ABO与△CDO关于O点中心对称,点E、F在线段AC上,且AF=CE.求证:FD=BE.
20.如图,在△ABC中,∠B=20°,∠ACB=30°,AB=2cm,△ABC逆时针旋转一定角度后与△ADE重合,且点C恰好成为AD的中点.
(1)指出旋转中心,并求出旋转的度数;
(2)求出∠BAE的度数和AE的长.
21.如图,四边形ABCD是正方形,△ADF绕着点A顺时旋转90°得到△ABE,若AF=4,AB=7.
(1)求DE的长度;
(2)指出BE与DF的关系如何?并说明由.
22.如图,已知:如图点,点在轴正半轴上,且,将线段绕点沿顺时针旋转,设点旋转后的对应点是点,求点的坐标.
23.将两块大小相同的含30°角的直角三角板(∠BAC=∠B1A1C=30°)按图1的方式放置,固定三角板A1B1C,然后将三角板ABC绕直角顶点C顺时针方向旋转(旋转角小于90°)至图2所示的位置,AB与A1C交于点E,AC与A1B1交于点F,AB与A1B1交于点O.
(1)求证:△BCE≌△B1CF;
(2)当旋转角等于30°时,AB与A1B1垂直吗?请说明理由.
24.如图,△DEF是△ABC经过某种变换得到的图形,点A与点D,点B与点E,点C与点F分别是对应点,观察点与点的坐标之间的关系,解答下列问题:
(1)分别写出点A与点D,点B与点E,点C与点F的坐标,并说说对应点的坐标有哪些特征;
(2)若点P(a+3,4﹣b)与点Q(2a,2b﹣3)也是通过上述变换得到的对应点,求a、b的值.
参考答案
一、选择题(每题3分,共30分)
题号 1 2 3 4 5 6 7 8 9 10
答案 B C C D C C A B A D
二、填空题(每题3分,共24分)
11.2.
12.
13.5
14.20°.
15.(1)(4)
16.【答案】
17.【答案】1.5
18.【答案】
三.解答题(共46分,19题6分,20 ---24题8分)
19.(证明:∵△ABO与△CDO关于O点中心对称,
∴OB=OD,OA=OC.
∵AF=CE,∴OF=OE.
∵在△DOF和△BOE中,
∴△DOF≌△BOE(SAS).
∴FD=BE.
20.解:(1)∠BAC=180°﹣∠B﹣∠ACB=180°﹣20°﹣30°=130°,
即∠BAD=130°,
∵△ABC逆时针旋转一定角度后与△ADE重合,
∴旋转中心为点A,旋转的度数为130°;
(2)∵△ABC逆时针旋转一定角度后与△ADE重合,
∴∠EAD=∠CAB=130°,AE=AC,AD=AB=2cm,
∴∠BAE=360°﹣130°﹣130°=100°,
∵点C恰好成为AD的中点,
∴AC=0.5AD=1cm,
∴AE=1cm.
21.(1)3;(2)BE=DF,BE⊥DF.
【详解】
解:(1)∵△ADF按顺时针方向旋转一定角度后得到△ABE,
∴AE=AF=4,AD=AB=7,
∴DE=AD﹣AE=7﹣4=3;
(2)BE、DF的关系为:BE=DF,BE⊥DF.理由如下:
∵△ADF按顺时针方向旋转一定角度后得到△ABE,
∴△ABE≌△ADF,
∴BE=DF,∠ABE=∠ADF,
∵∠ADF+∠F=180°﹣90°=90°,
∴∠ABE+∠F=90°,
∴BE⊥DF,
∴BE、DF的关系为:BE=DF,BE⊥DF.
22.点的坐标为.
【详解】
解:如图,作轴于,
∵,,
∴,
∵线段绕点沿逆时针旋转得,
∴,且,
∴
而,
∴,
在和中
,
∴,
∴,,
∴,
∴点的坐标为.
23.(1)证明:由题意得,BC=B1C,∠B=∠B1=60°,
又∵∠BCE+∠ECF=90°,
∠B1CF+∠ECF=90°,
∴∠BCE=∠B1CF,
在△BCE和△B1CF中,
,
∴△BCE≌△B1CF(ASA);
(2)当旋转角等于30°时,AB与A1B1垂直.理由如下:
证明:∵∠ECF=30°,
∴∠BCE=60°,
∴△BCE是等边三角形,
∴∠BEC=60°,得∠A1EO=60°,
又∵∠A1=30°,
∴∠A1EO=60°,
即AB与A1B1垂直.
24.解:(1)由图象可知,点A(2,3),点D(﹣2,﹣3),点B(1,2),点E(﹣1,﹣2),点C(3,1),
点F(﹣3,﹣1);
对应点的坐标特征为:横坐标、纵坐标都互为相反数;
(2)由(1)可知,a+3+2a=0,4﹣b+2b﹣3=0,解得a=﹣1,b=﹣1.
第二十三章 《旋转》单元测试卷
题号 一 二 三 总分
19 20 21 22 23 24
分数
一、选择题(每题3分,共30分)
1.在下列四个图案中既是轴对称图形,又是中心对称图形的是( )
A. B. C. D.
2如图,在Rt△ABC中,∠BAC=90°,将△ABC绕点A顺时针旋转90°后得到△AB′C′(点B的对应点是点B′,点C的对应点是点C′),连接CC′.若∠CC′B′=32°,则∠B的大小是( )
A.32° B.64° C.77° D.87°
3如图,紫荆花图案旋转一定角度后能与自身重合,则旋转的角度可能是( )
A.30° B.60° C.72° D.90°
4如图,在正方形ABCD中有一点E,把△ABE绕点B旋转到△CBF,连接EF,则△EBF的形状是( )
A.等边三角形 B.等腰三角形
C.直角三角形 D.等腰直角三角形
5.如图是由三个小正方形组成的图形,如果在图中补一个同样大小的正方形,使得补后的图形为轴对称图形,这样的补法有( )种.
A.2 B.3 C.4 D.5
6.如图,将△ABC绕点C按逆时针方向旋转至△DEC,使点D落在BC的延长线上.已知∠A=33°,∠B=30°,则∠ACE的大小是( )
A.63° B.58° C.54° D.52°
7.如图,四边形ABCD与四边形FGHE关于一个点成中心对称,则这个点是( )
A.O1 B.O2 C.O3 D.O4
8.如图,点O为矩形ABCD的对称中心,点E从点A出发沿AB向点B运动,移动到点B停止,延长EO交CD于点F,则四边形AECF形状的变化依次为( )
A.平行四边形→正方形→平行四边形→矩形
B.平行四边形→菱形→平行四边形→矩形
C.平行四边形→正方形→菱形→矩形
D.平行四边形→菱形→正方形→矩形
9.如图,△AOB中,∠ABO=90°,点B在x轴上,点A坐标为(2,2),将△AOB绕点O逆时针旋转15°,此时点A的对应点A'的坐标是( )
A.(,) B.(,) C.(,2) D.(1,)
10.下列各组图形中,△A'B'C'与△ABC成中心对称的是( )
A. B.
C. D.
二、填空题(每题3分,共24分)
11.如图,等腰直角△ABC中,∠ACB=90°,AC=BC=4,M为AB中点,D是射线BC上一动点,连接AD,将线段AD绕点A逆时针旋转90°得到线段AE,连接ED、ME,则点D在运动过程中ME的最小值为_____.
12.四边形、四边形都是正方形,当正方形绕点逆时针旋转45°()时,如图,连接,,并延长交于点,且.若,,则线段的长是________.
13.把一副三角板如图1放置,其中∠ACB=∠DEC=90°,斜边AB=6,DC=7,把三角板DCE绕着点C顺时针旋转使CD边恰好过AB的中点O,得到D1C1E1,如图2,则线段AD1的长度为_________.
14.如图,将三个同样的正方形的一个顶点重合放置,那么的度数为__________.
15.如图,点P为定角∠AOB的平分线上的一个定点,且∠MPN与∠AOB互补,若∠MPN在绕点P旋转的过程中,其两边分别与OA、OB相交于M、N两点,则以下结论:(1)PM=PN恒成立;(2)OM﹣ON的值不变;(3)△OMN的周长不变;(4)四边形PMON的面积不变,其中正确的序号为_____.
16.如图,将绕点旋转得到,改点的坐标为,则点的坐标为__________.
17.如图,在中,,,.将绕顶点按顺时针方向旋转到处,此时线段与的交点恰好为的中点,则线段__________.
18.如图,在正方形中,,把边绕点逆时针旋转得到线段,连接并延长交于点,连接,则三角形的面积为__________.
三.解答题(共46分,19题6分,20 ---24题8分)
19.如图,△ABO与△CDO关于O点中心对称,点E、F在线段AC上,且AF=CE.求证:FD=BE.
20.如图,在△ABC中,∠B=20°,∠ACB=30°,AB=2cm,△ABC逆时针旋转一定角度后与△ADE重合,且点C恰好成为AD的中点.
(1)指出旋转中心,并求出旋转的度数;
(2)求出∠BAE的度数和AE的长.
21.如图,四边形ABCD是正方形,△ADF绕着点A顺时旋转90°得到△ABE,若AF=4,AB=7.
(1)求DE的长度;
(2)指出BE与DF的关系如何?并说明由.
22.如图,已知:如图点,点在轴正半轴上,且,将线段绕点沿顺时针旋转,设点旋转后的对应点是点,求点的坐标.
23.将两块大小相同的含30°角的直角三角板(∠BAC=∠B1A1C=30°)按图1的方式放置,固定三角板A1B1C,然后将三角板ABC绕直角顶点C顺时针方向旋转(旋转角小于90°)至图2所示的位置,AB与A1C交于点E,AC与A1B1交于点F,AB与A1B1交于点O.
(1)求证:△BCE≌△B1CF;
(2)当旋转角等于30°时,AB与A1B1垂直吗?请说明理由.
24.如图,△DEF是△ABC经过某种变换得到的图形,点A与点D,点B与点E,点C与点F分别是对应点,观察点与点的坐标之间的关系,解答下列问题:
(1)分别写出点A与点D,点B与点E,点C与点F的坐标,并说说对应点的坐标有哪些特征;
(2)若点P(a+3,4﹣b)与点Q(2a,2b﹣3)也是通过上述变换得到的对应点,求a、b的值.
参考答案
一、选择题(每题3分,共30分)
题号 1 2 3 4 5 6 7 8 9 10
答案 B C C D C C A B A D
二、填空题(每题3分,共24分)
11.2.
12.
13.5
14.20°.
15.(1)(4)
16.【答案】
17.【答案】1.5
18.【答案】
三.解答题(共46分,19题6分,20 ---24题8分)
19.(证明:∵△ABO与△CDO关于O点中心对称,
∴OB=OD,OA=OC.
∵AF=CE,∴OF=OE.
∵在△DOF和△BOE中,
∴△DOF≌△BOE(SAS).
∴FD=BE.
20.解:(1)∠BAC=180°﹣∠B﹣∠ACB=180°﹣20°﹣30°=130°,
即∠BAD=130°,
∵△ABC逆时针旋转一定角度后与△ADE重合,
∴旋转中心为点A,旋转的度数为130°;
(2)∵△ABC逆时针旋转一定角度后与△ADE重合,
∴∠EAD=∠CAB=130°,AE=AC,AD=AB=2cm,
∴∠BAE=360°﹣130°﹣130°=100°,
∵点C恰好成为AD的中点,
∴AC=0.5AD=1cm,
∴AE=1cm.
21.(1)3;(2)BE=DF,BE⊥DF.
【详解】
解:(1)∵△ADF按顺时针方向旋转一定角度后得到△ABE,
∴AE=AF=4,AD=AB=7,
∴DE=AD﹣AE=7﹣4=3;
(2)BE、DF的关系为:BE=DF,BE⊥DF.理由如下:
∵△ADF按顺时针方向旋转一定角度后得到△ABE,
∴△ABE≌△ADF,
∴BE=DF,∠ABE=∠ADF,
∵∠ADF+∠F=180°﹣90°=90°,
∴∠ABE+∠F=90°,
∴BE⊥DF,
∴BE、DF的关系为:BE=DF,BE⊥DF.
22.点的坐标为.
【详解】
解:如图,作轴于,
∵,,
∴,
∵线段绕点沿逆时针旋转得,
∴,且,
∴
而,
∴,
在和中
,
∴,
∴,,
∴,
∴点的坐标为.
23.(1)证明:由题意得,BC=B1C,∠B=∠B1=60°,
又∵∠BCE+∠ECF=90°,
∠B1CF+∠ECF=90°,
∴∠BCE=∠B1CF,
在△BCE和△B1CF中,
,
∴△BCE≌△B1CF(ASA);
(2)当旋转角等于30°时,AB与A1B1垂直.理由如下:
证明:∵∠ECF=30°,
∴∠BCE=60°,
∴△BCE是等边三角形,
∴∠BEC=60°,得∠A1EO=60°,
又∵∠A1=30°,
∴∠A1EO=60°,
即AB与A1B1垂直.
24.解:(1)由图象可知,点A(2,3),点D(﹣2,﹣3),点B(1,2),点E(﹣1,﹣2),点C(3,1),
点F(﹣3,﹣1);
对应点的坐标特征为:横坐标、纵坐标都互为相反数;
(2)由(1)可知,a+3+2a=0,4﹣b+2b﹣3=0,解得a=﹣1,b=﹣1.
同课章节目录
