2022-2023学年鲁教版(五四学制)数学七年级上册暑假自主学习学情检测题(1-3章)(word版含答案)
文档属性
| 名称 | 2022-2023学年鲁教版(五四学制)数学七年级上册暑假自主学习学情检测题(1-3章)(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 344.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-23 08:31:46 | ||
图片预览




文档简介
2022-2023学年鲁教版(五四学制)七年级数学上册暑假自主学习学情检测测试题(附答案)
(内容范围:三角形、轴对称图形、勾股定理)
一、选择题(本大题共12小题,共36分.)
1.下面四个图形中,属于轴对称图形有( )
A.1个 B.2个 C.3个 D.4个
2.在△ABC和△DEF中,AB=DE,∠B=∠E,补充条件后仍不能证△ABC≌△DEF,则补充的这个条件是( )
A.BC=EF B.∠A=∠D C.AC=DF D.∠C=∠F
3.有两条线段的长度分别是5cm和10cm,如果再选取一条线段与其构成等腰三角形,则选取的线段长为( )
A.5cm B.6cm C.10cm D.5cm或10cm
4.如图所示,一圆柱高8cm,底面半径为2cm,一只蚂蚁从点A爬到点B处吃食,要爬行的最短路程(π取3)是( )
A.10cm B.14cm C.20cm D.无法确定
5.已知a,b,c为三角形的三边,化简|a+b﹣c|﹣|b﹣a﹣c|的结果是( )
A.0 B.2a C.2(a+c) D.2(b﹣c)
6.如图,△OAD≌△OBC,且∠O=70°,∠C=25°,则∠AEB的度数是( )
A.145° B.140° C.130° D.120°
7.一艘轮船以16海里∕小时的速度从港口A出发向东北方向航行,另一轮船12海里∕小时从港口A出发向东南方向航行,离开港口3小时后,则两船相距( )
A.36海里 B.48海里 C.60海里 D.84海里
8.如图,在△ABC中,AB=AC,∠C=30°,AB⊥AD,AD=2cm,则BC的长等于( )
A.8cm B.6cm C.4cm D.2cm
9.将一根长24cm的筷子,置于底面直径为5cm,高为12cm的圆柱形水杯中,设筷子露出在杯子外面长为hcm,则h的取值范围是( )
A.0≤h≤12 B.12≤h≤13 C.11≤h≤12 D.12≤h≤24
10.如图,在△ABC中,BD平分∠ABC,CD平分∠BCA,若∠D:∠A=7:2,则∠A的度数是( )
A.30° B.32° C.36° D.40°
11.下列说法错误的有( )
A.关于某直线对称的两个图形一定能完全重合
B.全等的两个三角形一定关于某直线对称
C.轴对称图形的对称轴至少有一条
D.线段是轴对称图形
12.如图,△ABC≌△AEF,点F在BC上,以下结论不正确的有( )
A.∠B=∠E B.∠AFC=∠C C.∠FAB=∠EFA D.∠EAB=∠FAC
二、填空题(本大题共6小题,共18分)
13.在△ABC中,∠B<∠C,AD为BC边的中线,△ABD的周长与△ADC的周长相差3,AB=8,则AC= .
14.如图,AC=BC,∠B=72°,AD平分∠BAC,则图中等腰三角形(不含△ABC)的个数是 .
15.如图,将三角形纸片的一角折叠,若∠A=65°,∠B=75°,∠1=30°,则∠2的度数为 .
16.如图,△ABC的周长是10,BO,CO分别平分∠ABC和∠ACB,OD⊥BC于D,且OD=3,则△ABC的面积是 .
17.定义:等腰三角形的顶角与其一个底角的度数的比值k称为这个等腰三角形的“特征值”.若等腰△ABC中,∠A=80°,则它的特征值k= .
18.如图是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的.若AC=6,BC=5,将四个直角三角形中边长为6的直角边分别向外延长一倍,得到如图所示的“数学风车”,则这个风车的外围周长是 .
三、解答题(本大题共7小题,共66分)
19.如图,在△ABC和△AED中,∠BAC=∠EAD,AB=AE,AC=AD,连接BD,CE,线段BD和EC相等吗?为什么?
20.如图,将长方形ABCD沿BD折叠,使点C落在C′处,BC′交AD于E,AD=8,AB=4,求重叠部分(即△BED)的面积.
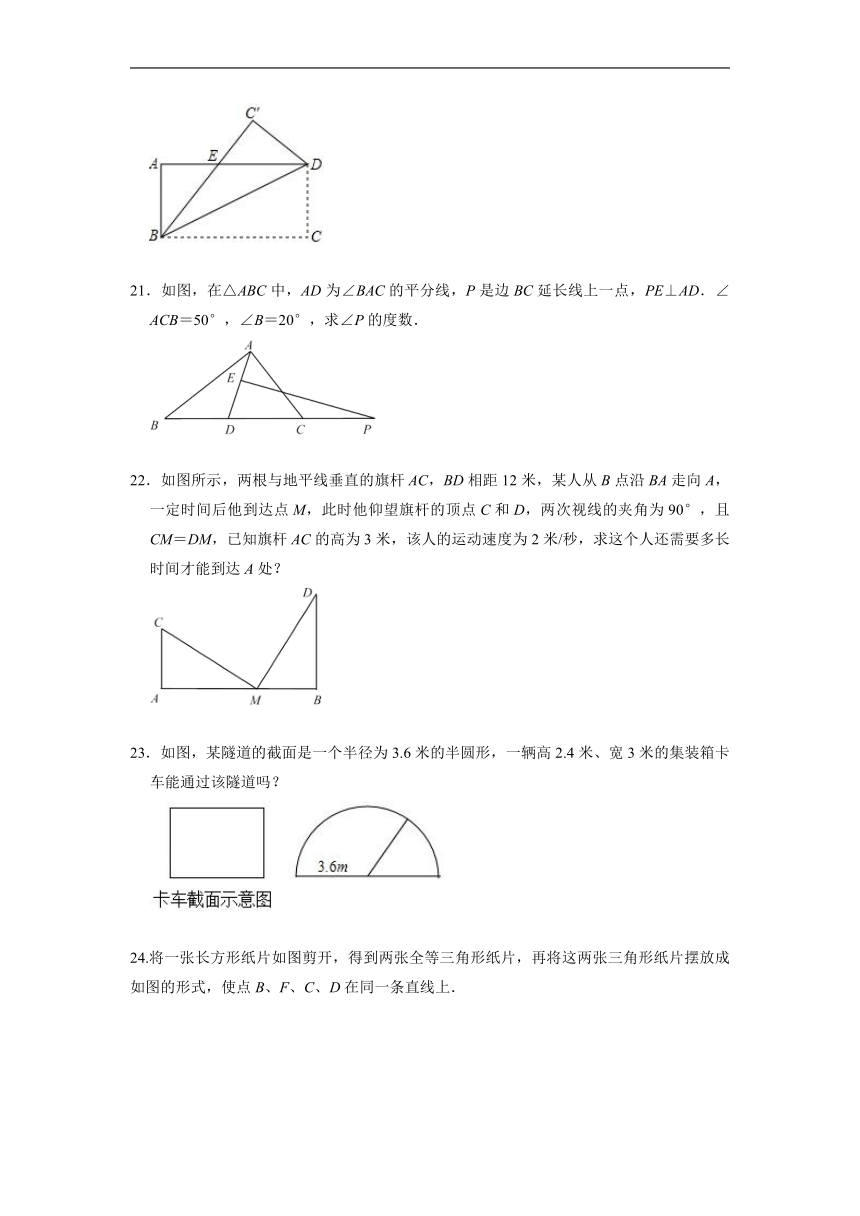
21.如图,在△ABC中,AD为∠BAC的平分线,P是边BC延长线上一点,PE⊥AD.∠ACB=50°,∠B=20°,求∠P的度数.
22.如图所示,两根与地平线垂直的旗杆AC,BD相距12米,某人从B点沿BA走向A,一定时间后他到达点M,此时他仰望旗杆的顶点C和D,两次视线的夹角为90°,且CM=DM,已知旗杆AC的高为3米,该人的运动速度为2米/秒,求这个人还需要多长时间才能到达A处?
23.如图,某隧道的截面是一个半径为3.6米的半圆形,一辆高2.4米、宽3米的集装箱卡车能通过该隧道吗?
24.将一张长方形纸片如图剪开,得到两张全等三角形纸片,再将这两张三角形纸片摆放成如图的形式,使点B、F、C、D在同一条直线上.
(1)求证:AB⊥ED;
(2)若PB=BC,请说明PE=BF.
25.(1)如图1,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE.说明BD=CE的理由;
(2)如图2,△ACB和△DCE均为等边三角形,点A,D,E在同一直线上,连接BE.直接写结论:∠AEB= °;
(3)如图3,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,AC=BC,CD=CE,点A,D,E在同一直线上,CM为△DCE的边DE上的高,连接BE.
①求∠AEB的度数;
②线段CM,AE,BE间有怎样的数量关系?写出结论并说明理由.
参考答案
一、选择题(本大题共12小题,共36分.)
1.解:第1个图形:不是轴对称图形,不合题意;
第2个图形:是轴对称图形,符合题意;
第3个图形:不是轴对称图形,不合题意;
第4个图形:是轴对称图形,符合题意;
故选:B.
2.解:A、补充条件BC=EF可利用SAS证明三角形全等,故此选项不合题意;
B、补充条件∠A=∠D可利用ASA证明三角形全等,故此选项不合题意;
C、补充条件AC=DF不能证明三角形全等,故此选项符合题意;
D、补充条件∠C=∠F可利用AAS证明三角形全等,故此选项不合题意;
故选:C.
3.解:∵有两条线段长度分别为:5cm,10cm,
∴设第三条边长为:a,
故10﹣5<a<10+5,
则5<a<15,
故如果再选取一条线段与其构成等腰三角形,则选取的线段长为10cm.
故选:C.
4.解:如图所示:沿AC将圆柱的侧面展开,
∵底面半径为2cm,
∴BC==2π≈6cm,
在Rt△ABC中,
∵AC=8cm,BC=6cm,
∴AB==10cm.
故选:A.
5.解:∵a,b,c为三角形的三边,
∴a+b﹣c>0,b﹣a﹣c<0,
∴|a+b﹣c|﹣|b﹣a﹣c|
=a+b﹣c﹣[﹣(b﹣a﹣c)]
=a+b﹣c+b﹣a﹣c
=2(b﹣c).
故选:D.
6.解:∵△OAD≌△OBC,
∴∠OBC=∠OAD,
∵∠O=70°,∠C=25°,
∴∠OBC=∠OAD=85°,
则∠AEB=360°﹣70°﹣170°=120°.
故选:D.
7.解:∵两船行驶的方向是东北方向和东南方向,
∴∠BAC=90°,
两小时后,两艘船分别行驶了16×3=48,12×3=36海里,
根据勾股定理得:=60(海里).
故选:C.
8.解:∵AB=AC,∠C=30°,
∴∠B=∠C=30°,
∴∠BAC=120°,
∵AB⊥AD,AD=2cm,
∴∠BAD=90°,BD=2AD=4cm,
∴∠DAC=120°﹣90°=30°,
∴AD=CD=2cm,
∴CB=DB+CD=6cm.
故选:B.
9.解:当筷子与杯底垂直时h最大,h最大=24﹣12=12(cm).
当筷子与杯底及杯高构成直角三角形时h最小,
如图所示:此时,AB===13(cm),
故h=24﹣13=11(cm).
故h的取值范围是:11cm≤h≤12cm.
故选:C.
10.解:∵∠ABC+∠ACB=180°﹣∠A,BD平分∠ABC,CD平分∠BCA,
∴∠DCB+∠DBCA=(∠ABC+∠ACB)=(180°﹣∠A)=90°﹣∠A,
∴∠D=180°﹣(∠DCB+∠DBCA)=180°﹣(90°﹣∠A)=180°﹣90°+∠A=90°+∠A.
∵∠D:∠A=7:2,
∴90°+∠A=∠A,
解得∠A=30°.
故选:A.
11.解:A.关于某直线对称的两个图形一定能完全重合,正确,不合题意;
B.全等的两个三角形不一定关于某直线对称,原说法错误,符合题意;
C.轴对称图形的对称轴至少有一条,正确,不合题意;
D.线段是轴对称图形,正确,不合题意;
故选:B.
12.解:A、∵△ABC≌△AEF,
∴∠B=∠E,本选项说法正确,不符合题意;
B、∵△ABC≌△AEF,
∴AC=AF,
∴∠AFC=∠C,本选项说法正确,不符合题意;
C、当△ABC≌△AEF时,∠AFC与∠C的大小不能确定,本选项说法不正确,符合题意;
D、∵△ABC≌△AEF,
∴∠EAF=∠BAC
∴∠EAF﹣∠BAF=∠BAC﹣∠BAF,即∠EAB=∠FAC,本选项说法正确,不符合题意;
故选:C.
二、填空题(本大题共6小题,共18分果)
13.解:如图:
∵AD为BC边的中线,
∴BD=CD,
∵△ABD与△ADC的周长差为3,AB=8,∠B<∠C,
∴C△ABD﹣C△ADC=(AB+AD+BD)﹣(AC+AD+CD)=AB﹣AC=8﹣AC=3,
解得AC=5.
故答案为:5.
14.解:由图可知,∵AC=BC,∠B=72°,
∴∠C=36°,
∵AD平分∠BAC,
∴∠CAD=∠BAD=∠C=36°
∴△CAD为等腰三角形,
∵∠BDA=∠C+∠CAD=72°=∠B,
∴△BAD为等腰三角形,
∴则图中等腰三角形(不含△ABC)的个数是2个.
故答案为2.
15.解:如图,延长AD、BE交于点C′,并连接CC′.
由题意得:△DEC≌△DEC′.
∴∠DCE=∠DC′E.
∵∠A=65°,∠B=75°,
∴∠DC′E=180°﹣(∠A+∠B)=180°﹣(65°+75°)=40°.
∵∠1=∠DCC′+∠CC′D,∠2=∠ECC′+∠EC′C,
∴∠1+∠2=∠DCC′+∠DC′C+∠ECC′+∠EC′C=∠DCE+∠DC′E=2∠DC′E=80°.
又∵∠1=30°,
∴∠2=50°.
故答案为:50°.
16.解:连接OA,过点O作OE⊥AB于E,OF⊥AC于F,
∵△ABC的周长是10,
∴AB+AC+BC=10,
∵BO,CO分别平分∠ABC和∠ACB,OD⊥BC,OE⊥AB,OF⊥AC,OD=3,
∴OE=OF=OD=3,
∴S△ABC=×AB×OE+×AC×OF+×BC×OD=×10×3=15,
故答案为:15.
17.解:
①当∠A为顶角时,等腰三角形两底角的度数为:=50°
∴特征值k==
②当∠A为底角时,顶角的度数为:180°﹣80°﹣80°=20°
∴特征值k==
综上所述,特征值k为或
故答案为或
18.解:设将AC延长到点D,连接BD,
根据题意,得CD=6×2=12,BC=5.
∵∠BCD=90°
∴BC2+CD2=BD2,即52+122=BD2
∴BD=13
∴AD+BD=6+13=19
∴这个风车的外围周长是19×4=76.
故答案为:76.
三、解答题(本大题共7小题,共66分)
19.解:相等,理由如下:
∵∠DAE=∠BAC,
∴∠DAE﹣∠BAE=∠BAC﹣∠BAE,
∴∠BAD=∠EAC,
在△BAD与△EAC中,
,
∴△BAD≌△EAC(SAS),
∴BD=EC.
20.解:∵AD∥BC,
∴∠DBC=∠BDA;
∵∠C′BD=∠DBC,
∴∠C′BD=∠BDA,
∴DE=BE,
设DE=x,则AE=8﹣x
在Rt△ABE中,x2=42+(8﹣x)2
解得x=5,
∴S△DBE=×5×4=10.
21.解:∵∠ACB=50°,∠B=20°,
∴∠BAC=180°﹣(∠B+∠ACB)=110°.
∵AD平分∠BAC,
∴∠BAD==55°.
∴∠ADC=∠B+∠BAD=75°.
∵EP⊥AD,
∴∠AEP=90°.
∴∠P=∠AEP﹣∠ADP=15°.
22.解:∵∠CMD=90°,
∴∠CMA+∠DMB=90°,
∵∠CAM=∠DBM=90°,
∴∠CMA+∠ACM=90°,
∴∠ACM=∠DMB,
在△ACM和△BMD中,
,
∴△ACM≌△BMD(AAS),
∴AC=BM=3米,
∴AM=12﹣3=9(米),
∴他到达点A时,还需要的运动时间为9÷2=4.5秒.
答:还需要4.5秒才能到达A.
23.解:图中的长方形ABCD是卡车横截面的示意图,AB的中点O是隧道的截面半圆的圆心,
OB==1.5m,BC=2.4m,∠OBC=90°,
在Rt△OBC中,由勾股定理,得OB2+BC2=OC2,
即OC2=BC2+OB2=2.42+1.52=8.01,
∵3.62=12.96,
∴12.96>8.01.
∴卡车能通过该隧道.
24.证明:(1)依题意可得,∠A+∠B=90°,∠A=∠D,
∴∠D+∠B=90°,
∴∠BPD=90°,
∴AB⊥DE;
(2)∵将一张长方形纸片沿着对角线剪开,得到两张三角形纸片,
∴△ABC≌△DEF,
∴∠A=∠D,AB=DE,
在△BPD与△BCA中,
∵,
∴△BPD≌△BCA(AAS),
∴BD=AB=DE,DF=DP,
∴BD﹣DF=DE﹣DP,
即PE=BF.
25.解:(1)∵∠BAC=∠DAE,
∴∠BAC﹣∠DAC=∠DAE﹣∠DAE,
即:∠BAD=∠CAE,
在△BAD和△CAE中,
,
∴△BAD≌△CAE(SAS),
∴BD=CE;
(2)∵△ACB和△DCE均为等边三角形,
∴AC=CB,CD=CE,∠ACB=∠DCE=∠CDE=∠CED=60°,
∴∠ACD=∠BCE,
∴△ACD≌△BCE(SAS),
∴∠BCE=∠ADC=180°﹣∠CDE=120°,
∴∠AEC=∠BEC﹣∠CED=60°,
故答案是60°;
(3))①∵△ACB和△DCE均为等腰直角三角形,
∴AC=CB,CD=CE,∠ACB=∠DCE=90°,∠CDE=∠CED=45°,
∴∠ACB﹣∠DCB=∠DCE﹣∠DCB,
∴∠ACD=∠BCE,
∴△ACD≌△BCE(SAS),
∴∠BCE=∠ADC=180°﹣∠CDE=135°,
∴∠AEC=∠BEC﹣∠CED=135°﹣45°=90°,
②由①知,
△ACD≌△BCE,
∴BE=AD,
在Rt△DCE中,CM⊥DE,
∴DM=ME,
∴DE=2CM,
∵AE=AD+DE,
∴AE=BE+2CM.
(内容范围:三角形、轴对称图形、勾股定理)
一、选择题(本大题共12小题,共36分.)
1.下面四个图形中,属于轴对称图形有( )
A.1个 B.2个 C.3个 D.4个
2.在△ABC和△DEF中,AB=DE,∠B=∠E,补充条件后仍不能证△ABC≌△DEF,则补充的这个条件是( )
A.BC=EF B.∠A=∠D C.AC=DF D.∠C=∠F
3.有两条线段的长度分别是5cm和10cm,如果再选取一条线段与其构成等腰三角形,则选取的线段长为( )
A.5cm B.6cm C.10cm D.5cm或10cm
4.如图所示,一圆柱高8cm,底面半径为2cm,一只蚂蚁从点A爬到点B处吃食,要爬行的最短路程(π取3)是( )
A.10cm B.14cm C.20cm D.无法确定
5.已知a,b,c为三角形的三边,化简|a+b﹣c|﹣|b﹣a﹣c|的结果是( )
A.0 B.2a C.2(a+c) D.2(b﹣c)
6.如图,△OAD≌△OBC,且∠O=70°,∠C=25°,则∠AEB的度数是( )
A.145° B.140° C.130° D.120°
7.一艘轮船以16海里∕小时的速度从港口A出发向东北方向航行,另一轮船12海里∕小时从港口A出发向东南方向航行,离开港口3小时后,则两船相距( )
A.36海里 B.48海里 C.60海里 D.84海里
8.如图,在△ABC中,AB=AC,∠C=30°,AB⊥AD,AD=2cm,则BC的长等于( )
A.8cm B.6cm C.4cm D.2cm
9.将一根长24cm的筷子,置于底面直径为5cm,高为12cm的圆柱形水杯中,设筷子露出在杯子外面长为hcm,则h的取值范围是( )
A.0≤h≤12 B.12≤h≤13 C.11≤h≤12 D.12≤h≤24
10.如图,在△ABC中,BD平分∠ABC,CD平分∠BCA,若∠D:∠A=7:2,则∠A的度数是( )
A.30° B.32° C.36° D.40°
11.下列说法错误的有( )
A.关于某直线对称的两个图形一定能完全重合
B.全等的两个三角形一定关于某直线对称
C.轴对称图形的对称轴至少有一条
D.线段是轴对称图形
12.如图,△ABC≌△AEF,点F在BC上,以下结论不正确的有( )
A.∠B=∠E B.∠AFC=∠C C.∠FAB=∠EFA D.∠EAB=∠FAC
二、填空题(本大题共6小题,共18分)
13.在△ABC中,∠B<∠C,AD为BC边的中线,△ABD的周长与△ADC的周长相差3,AB=8,则AC= .
14.如图,AC=BC,∠B=72°,AD平分∠BAC,则图中等腰三角形(不含△ABC)的个数是 .
15.如图,将三角形纸片的一角折叠,若∠A=65°,∠B=75°,∠1=30°,则∠2的度数为 .
16.如图,△ABC的周长是10,BO,CO分别平分∠ABC和∠ACB,OD⊥BC于D,且OD=3,则△ABC的面积是 .
17.定义:等腰三角形的顶角与其一个底角的度数的比值k称为这个等腰三角形的“特征值”.若等腰△ABC中,∠A=80°,则它的特征值k= .
18.如图是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的.若AC=6,BC=5,将四个直角三角形中边长为6的直角边分别向外延长一倍,得到如图所示的“数学风车”,则这个风车的外围周长是 .
三、解答题(本大题共7小题,共66分)
19.如图,在△ABC和△AED中,∠BAC=∠EAD,AB=AE,AC=AD,连接BD,CE,线段BD和EC相等吗?为什么?
20.如图,将长方形ABCD沿BD折叠,使点C落在C′处,BC′交AD于E,AD=8,AB=4,求重叠部分(即△BED)的面积.
21.如图,在△ABC中,AD为∠BAC的平分线,P是边BC延长线上一点,PE⊥AD.∠ACB=50°,∠B=20°,求∠P的度数.
22.如图所示,两根与地平线垂直的旗杆AC,BD相距12米,某人从B点沿BA走向A,一定时间后他到达点M,此时他仰望旗杆的顶点C和D,两次视线的夹角为90°,且CM=DM,已知旗杆AC的高为3米,该人的运动速度为2米/秒,求这个人还需要多长时间才能到达A处?
23.如图,某隧道的截面是一个半径为3.6米的半圆形,一辆高2.4米、宽3米的集装箱卡车能通过该隧道吗?
24.将一张长方形纸片如图剪开,得到两张全等三角形纸片,再将这两张三角形纸片摆放成如图的形式,使点B、F、C、D在同一条直线上.
(1)求证:AB⊥ED;
(2)若PB=BC,请说明PE=BF.
25.(1)如图1,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE.说明BD=CE的理由;
(2)如图2,△ACB和△DCE均为等边三角形,点A,D,E在同一直线上,连接BE.直接写结论:∠AEB= °;
(3)如图3,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,AC=BC,CD=CE,点A,D,E在同一直线上,CM为△DCE的边DE上的高,连接BE.
①求∠AEB的度数;
②线段CM,AE,BE间有怎样的数量关系?写出结论并说明理由.
参考答案
一、选择题(本大题共12小题,共36分.)
1.解:第1个图形:不是轴对称图形,不合题意;
第2个图形:是轴对称图形,符合题意;
第3个图形:不是轴对称图形,不合题意;
第4个图形:是轴对称图形,符合题意;
故选:B.
2.解:A、补充条件BC=EF可利用SAS证明三角形全等,故此选项不合题意;
B、补充条件∠A=∠D可利用ASA证明三角形全等,故此选项不合题意;
C、补充条件AC=DF不能证明三角形全等,故此选项符合题意;
D、补充条件∠C=∠F可利用AAS证明三角形全等,故此选项不合题意;
故选:C.
3.解:∵有两条线段长度分别为:5cm,10cm,
∴设第三条边长为:a,
故10﹣5<a<10+5,
则5<a<15,
故如果再选取一条线段与其构成等腰三角形,则选取的线段长为10cm.
故选:C.
4.解:如图所示:沿AC将圆柱的侧面展开,
∵底面半径为2cm,
∴BC==2π≈6cm,
在Rt△ABC中,
∵AC=8cm,BC=6cm,
∴AB==10cm.
故选:A.
5.解:∵a,b,c为三角形的三边,
∴a+b﹣c>0,b﹣a﹣c<0,
∴|a+b﹣c|﹣|b﹣a﹣c|
=a+b﹣c﹣[﹣(b﹣a﹣c)]
=a+b﹣c+b﹣a﹣c
=2(b﹣c).
故选:D.
6.解:∵△OAD≌△OBC,
∴∠OBC=∠OAD,
∵∠O=70°,∠C=25°,
∴∠OBC=∠OAD=85°,
则∠AEB=360°﹣70°﹣170°=120°.
故选:D.
7.解:∵两船行驶的方向是东北方向和东南方向,
∴∠BAC=90°,
两小时后,两艘船分别行驶了16×3=48,12×3=36海里,
根据勾股定理得:=60(海里).
故选:C.
8.解:∵AB=AC,∠C=30°,
∴∠B=∠C=30°,
∴∠BAC=120°,
∵AB⊥AD,AD=2cm,
∴∠BAD=90°,BD=2AD=4cm,
∴∠DAC=120°﹣90°=30°,
∴AD=CD=2cm,
∴CB=DB+CD=6cm.
故选:B.
9.解:当筷子与杯底垂直时h最大,h最大=24﹣12=12(cm).
当筷子与杯底及杯高构成直角三角形时h最小,
如图所示:此时,AB===13(cm),
故h=24﹣13=11(cm).
故h的取值范围是:11cm≤h≤12cm.
故选:C.
10.解:∵∠ABC+∠ACB=180°﹣∠A,BD平分∠ABC,CD平分∠BCA,
∴∠DCB+∠DBCA=(∠ABC+∠ACB)=(180°﹣∠A)=90°﹣∠A,
∴∠D=180°﹣(∠DCB+∠DBCA)=180°﹣(90°﹣∠A)=180°﹣90°+∠A=90°+∠A.
∵∠D:∠A=7:2,
∴90°+∠A=∠A,
解得∠A=30°.
故选:A.
11.解:A.关于某直线对称的两个图形一定能完全重合,正确,不合题意;
B.全等的两个三角形不一定关于某直线对称,原说法错误,符合题意;
C.轴对称图形的对称轴至少有一条,正确,不合题意;
D.线段是轴对称图形,正确,不合题意;
故选:B.
12.解:A、∵△ABC≌△AEF,
∴∠B=∠E,本选项说法正确,不符合题意;
B、∵△ABC≌△AEF,
∴AC=AF,
∴∠AFC=∠C,本选项说法正确,不符合题意;
C、当△ABC≌△AEF时,∠AFC与∠C的大小不能确定,本选项说法不正确,符合题意;
D、∵△ABC≌△AEF,
∴∠EAF=∠BAC
∴∠EAF﹣∠BAF=∠BAC﹣∠BAF,即∠EAB=∠FAC,本选项说法正确,不符合题意;
故选:C.
二、填空题(本大题共6小题,共18分果)
13.解:如图:
∵AD为BC边的中线,
∴BD=CD,
∵△ABD与△ADC的周长差为3,AB=8,∠B<∠C,
∴C△ABD﹣C△ADC=(AB+AD+BD)﹣(AC+AD+CD)=AB﹣AC=8﹣AC=3,
解得AC=5.
故答案为:5.
14.解:由图可知,∵AC=BC,∠B=72°,
∴∠C=36°,
∵AD平分∠BAC,
∴∠CAD=∠BAD=∠C=36°
∴△CAD为等腰三角形,
∵∠BDA=∠C+∠CAD=72°=∠B,
∴△BAD为等腰三角形,
∴则图中等腰三角形(不含△ABC)的个数是2个.
故答案为2.
15.解:如图,延长AD、BE交于点C′,并连接CC′.
由题意得:△DEC≌△DEC′.
∴∠DCE=∠DC′E.
∵∠A=65°,∠B=75°,
∴∠DC′E=180°﹣(∠A+∠B)=180°﹣(65°+75°)=40°.
∵∠1=∠DCC′+∠CC′D,∠2=∠ECC′+∠EC′C,
∴∠1+∠2=∠DCC′+∠DC′C+∠ECC′+∠EC′C=∠DCE+∠DC′E=2∠DC′E=80°.
又∵∠1=30°,
∴∠2=50°.
故答案为:50°.
16.解:连接OA,过点O作OE⊥AB于E,OF⊥AC于F,
∵△ABC的周长是10,
∴AB+AC+BC=10,
∵BO,CO分别平分∠ABC和∠ACB,OD⊥BC,OE⊥AB,OF⊥AC,OD=3,
∴OE=OF=OD=3,
∴S△ABC=×AB×OE+×AC×OF+×BC×OD=×10×3=15,
故答案为:15.
17.解:
①当∠A为顶角时,等腰三角形两底角的度数为:=50°
∴特征值k==
②当∠A为底角时,顶角的度数为:180°﹣80°﹣80°=20°
∴特征值k==
综上所述,特征值k为或
故答案为或
18.解:设将AC延长到点D,连接BD,
根据题意,得CD=6×2=12,BC=5.
∵∠BCD=90°
∴BC2+CD2=BD2,即52+122=BD2
∴BD=13
∴AD+BD=6+13=19
∴这个风车的外围周长是19×4=76.
故答案为:76.
三、解答题(本大题共7小题,共66分)
19.解:相等,理由如下:
∵∠DAE=∠BAC,
∴∠DAE﹣∠BAE=∠BAC﹣∠BAE,
∴∠BAD=∠EAC,
在△BAD与△EAC中,
,
∴△BAD≌△EAC(SAS),
∴BD=EC.
20.解:∵AD∥BC,
∴∠DBC=∠BDA;
∵∠C′BD=∠DBC,
∴∠C′BD=∠BDA,
∴DE=BE,
设DE=x,则AE=8﹣x
在Rt△ABE中,x2=42+(8﹣x)2
解得x=5,
∴S△DBE=×5×4=10.
21.解:∵∠ACB=50°,∠B=20°,
∴∠BAC=180°﹣(∠B+∠ACB)=110°.
∵AD平分∠BAC,
∴∠BAD==55°.
∴∠ADC=∠B+∠BAD=75°.
∵EP⊥AD,
∴∠AEP=90°.
∴∠P=∠AEP﹣∠ADP=15°.
22.解:∵∠CMD=90°,
∴∠CMA+∠DMB=90°,
∵∠CAM=∠DBM=90°,
∴∠CMA+∠ACM=90°,
∴∠ACM=∠DMB,
在△ACM和△BMD中,
,
∴△ACM≌△BMD(AAS),
∴AC=BM=3米,
∴AM=12﹣3=9(米),
∴他到达点A时,还需要的运动时间为9÷2=4.5秒.
答:还需要4.5秒才能到达A.
23.解:图中的长方形ABCD是卡车横截面的示意图,AB的中点O是隧道的截面半圆的圆心,
OB==1.5m,BC=2.4m,∠OBC=90°,
在Rt△OBC中,由勾股定理,得OB2+BC2=OC2,
即OC2=BC2+OB2=2.42+1.52=8.01,
∵3.62=12.96,
∴12.96>8.01.
∴卡车能通过该隧道.
24.证明:(1)依题意可得,∠A+∠B=90°,∠A=∠D,
∴∠D+∠B=90°,
∴∠BPD=90°,
∴AB⊥DE;
(2)∵将一张长方形纸片沿着对角线剪开,得到两张三角形纸片,
∴△ABC≌△DEF,
∴∠A=∠D,AB=DE,
在△BPD与△BCA中,
∵,
∴△BPD≌△BCA(AAS),
∴BD=AB=DE,DF=DP,
∴BD﹣DF=DE﹣DP,
即PE=BF.
25.解:(1)∵∠BAC=∠DAE,
∴∠BAC﹣∠DAC=∠DAE﹣∠DAE,
即:∠BAD=∠CAE,
在△BAD和△CAE中,
,
∴△BAD≌△CAE(SAS),
∴BD=CE;
(2)∵△ACB和△DCE均为等边三角形,
∴AC=CB,CD=CE,∠ACB=∠DCE=∠CDE=∠CED=60°,
∴∠ACD=∠BCE,
∴△ACD≌△BCE(SAS),
∴∠BCE=∠ADC=180°﹣∠CDE=120°,
∴∠AEC=∠BEC﹣∠CED=60°,
故答案是60°;
(3))①∵△ACB和△DCE均为等腰直角三角形,
∴AC=CB,CD=CE,∠ACB=∠DCE=90°,∠CDE=∠CED=45°,
∴∠ACB﹣∠DCB=∠DCE﹣∠DCB,
∴∠ACD=∠BCE,
∴△ACD≌△BCE(SAS),
∴∠BCE=∠ADC=180°﹣∠CDE=135°,
∴∠AEC=∠BEC﹣∠CED=135°﹣45°=90°,
②由①知,
△ACD≌△BCE,
∴BE=AD,
在Rt△DCE中,CM⊥DE,
∴DM=ME,
∴DE=2CM,
∵AE=AD+DE,
∴AE=BE+2CM.
