人教版八年级数学上册12.2 三角形全等的判定 同步训练(word、含解析)
文档属性
| 名称 | 人教版八年级数学上册12.2 三角形全等的判定 同步训练(word、含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 437.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-22 17:28:18 | ||
图片预览


文档简介
人教版八年级数学上册12.2 三角形全等的判定 同步训练
一、单选题
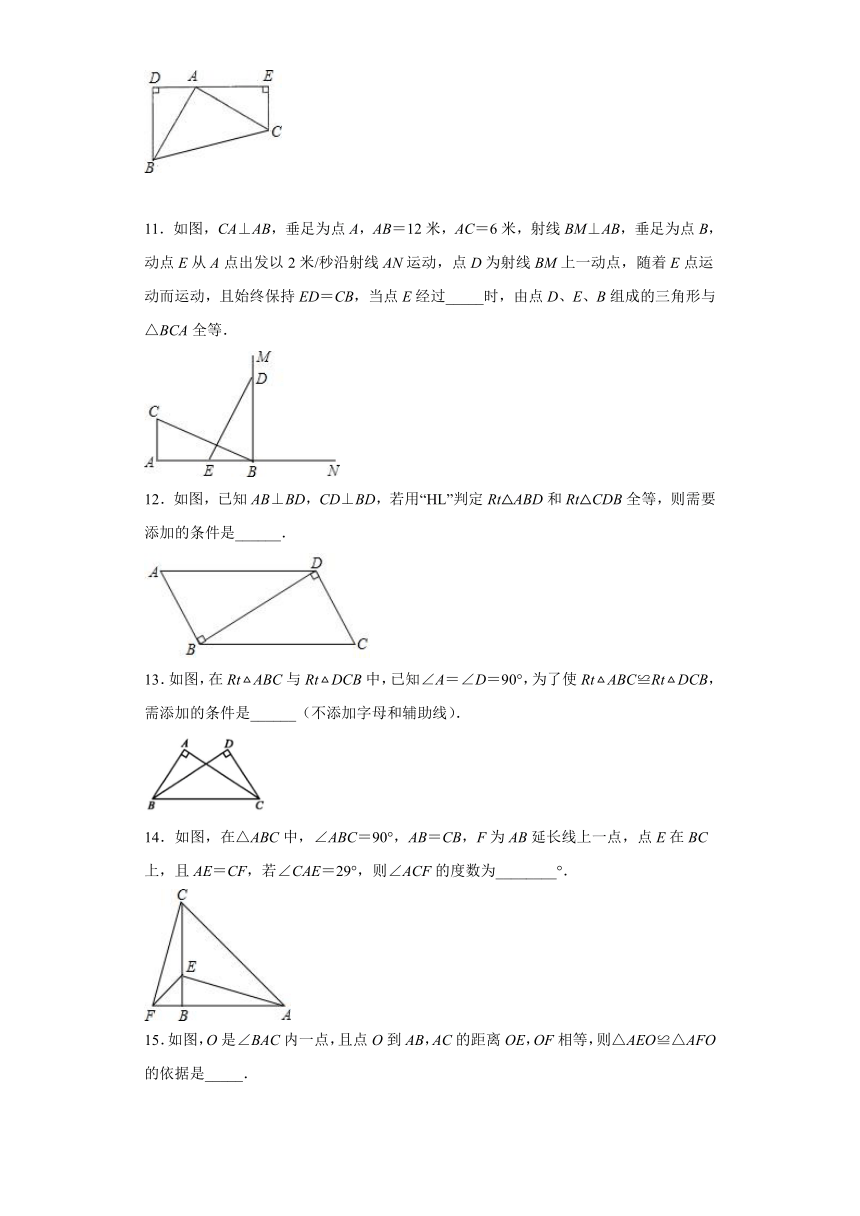
1.如图,甲、乙、丙三个三角形和左侧△ABC全等的是( )
A.甲和乙 B.甲和丙 C.乙和丙 D.只有丙
2.下列条件,不能判定的是( )
A.,, B.,,
C.,, D.,,
3.如图,已知∠1=∠2,AC=AD,增加下列条件之一:①AB=AE;②BC=ED;③∠C=∠D;④∠B=∠E.其中能使△ABC≌△AED的条件有( )
A.1个 B.2个 C.3个 D.4个
4.如图,已知矩形纸片,,,点在边上,将沿折叠,点落在点处,,分别交于点,,且,则的长为( )
A. B. C. D.
5.两个直角三角形中:①一锐角和斜边对应相等;②斜边和一直角边对应相等;③有两条边相等;④两个锐角对应相等.能使这两个直角三角形全等的是( )
A.①② B.②③ C.③④ D.①②③④
6.用直尺和圆规作一个角的平分线的示意图如图所示,则能说明∠AOC=∠BOC的依据是( )
A.全等三角形的定义 B.SSS C.ASA D.AAS
7.如图,点B、E、C、F四点共线,∠B =∠DEF,BE = CF,添加一个条件,不能判定 △ABC ≌ △DEF的是( )
A.∠A=∠D B.AB=DE C.AC∥DF D.AC=DF
8.如图,已知AE=AD,添加下列条件不能判定 △ACD≌△ABE的是( )
A.AB=AC B.BE=DC C.∠B=∠C D.∠AEB=∠ADC
二、填空题
9.如图,点B、F、C、E在一条直线上,ABED, AB=DE,要使△ABC≌△DEF,可以添加的一个条件是:________.
10.如图,在Rt△ABC中,∠BAC=90°,AB=AC,分别过点B,C作过点A的直线的垂线BD,CE,若BD=7cm,CE=5cm,则DE=________cm.
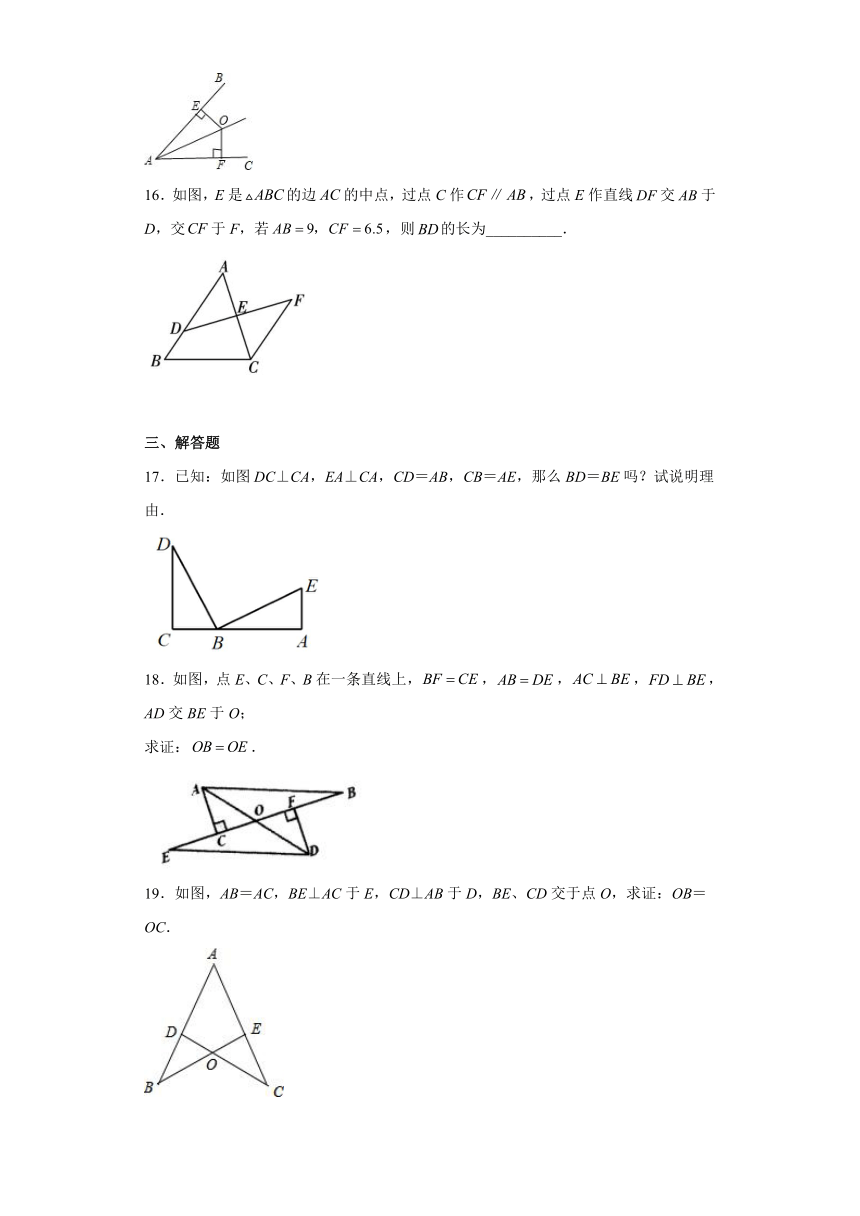
11.如图,CA⊥AB,垂足为点A,AB=12米,AC=6米,射线BM⊥AB,垂足为点B,动点E从A点出发以2米/秒沿射线AN运动,点D为射线BM上一动点,随着E点运动而运动,且始终保持ED=CB,当点E经过_____时,由点D、E、B组成的三角形与△BCA全等.
12.如图,已知AB⊥BD,CD⊥BD,若用“HL”判定Rt△ABD和Rt△CDB全等,则需要添加的条件是______.
13.如图,在RtABC与RtDCB中,已知∠A=∠D=90°,为了使RtABC≌RtDCB,需添加的条件是______(不添加字母和辅助线).
14.如图,在△ABC中,∠ABC=90°,AB=CB,F为AB延长线上一点,点E在BC上,且AE=CF,若∠CAE=29°,则∠ACF的度数为________°.
15.如图,O是∠BAC内一点,且点O到AB,AC的距离OE,OF相等,则△AEO≌△AFO的依据是_____.
16.如图,E是的边的中点,过点C作,过点E作直线交于D,交于F,若,则的长为__________.
三、解答题
17.已知:如图DC⊥CA,EA⊥CA,CD=AB,CB=AE,那么BD=BE吗?试说明理由.
18.如图,点E、C、F、B在一条直线上,,,,,AD交BE于O;
求证:.
19.如图,AB=AC,BE⊥AC于E,CD⊥AB于D,BE、CD交于点O,求证:OB=OC.
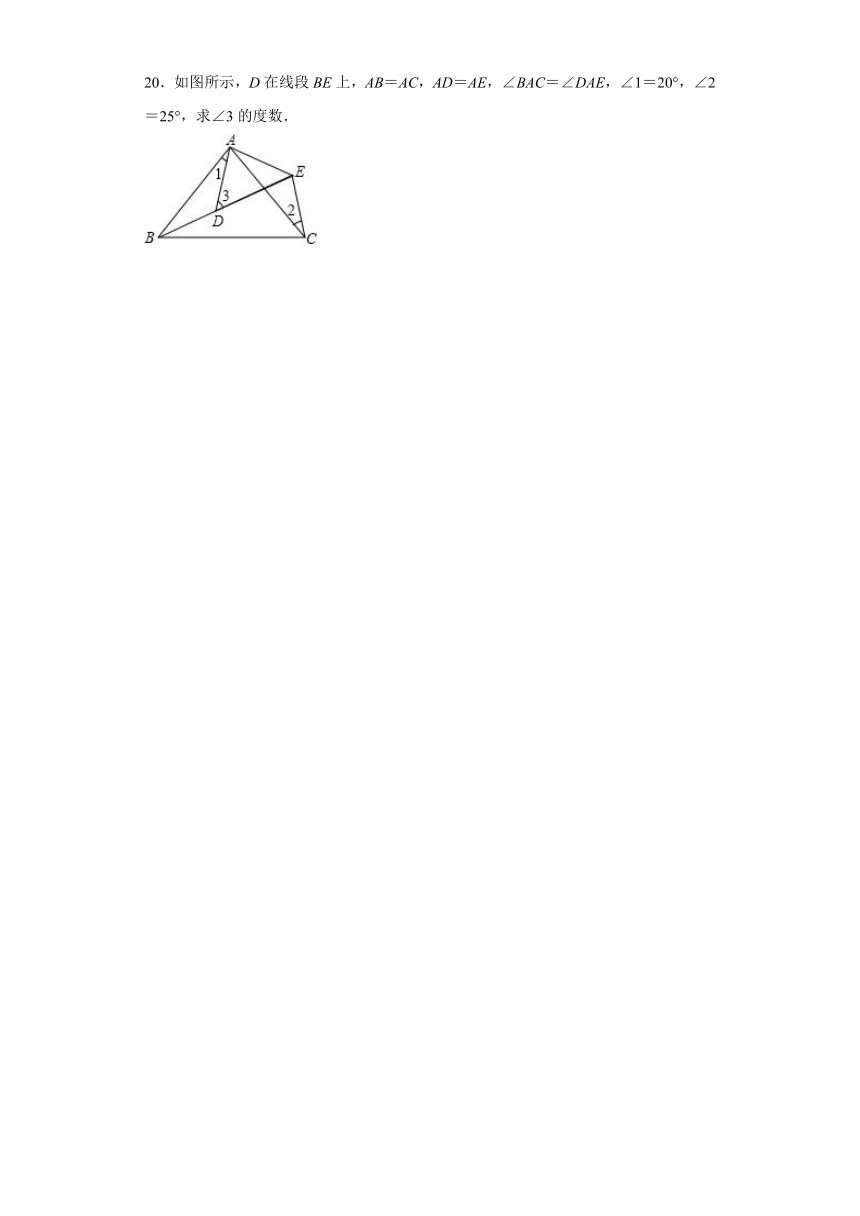
20.如图所示,D在线段BE上,AB=AC,AD=AE,∠BAC=∠DAE,∠1=20°,∠2=25°,求∠3的度数.
试卷第1页,共3页
参考答案:
1.C
【分析】根据三角形全等的判定方法得出乙和丙与△ABC全等,甲与△ABC不全等.
【详解】解:在△ABC和乙的三角形中,两边及其夹角对应相等,满足三角形全等的判定方法:SAS,
所以乙和△ABC全等;
在△ABC和丙的三角形中,两个及一角对边对应相等,满足三角形全等的判定方法:AAS,
所以丙和△ABC全等;
在△ABC和甲的三角形中,只有一边一角对应相等南,不能判定甲与△ABC全等;
故选:C.
【点睛】本题考查了三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.
2.A
【分析】根据全等三角形的判定SSS,AAS,ASA,SAS,进行判断即可得.
【详解】解:A、∠A=∠A′,AB=A′B′,,根据SSA不能推出,选项说法错误,不符合题意;
B、,,,根据ASA即可推出,选项说法正确,符合题意;
C、,,,根据AAS即可推出,选项说法正确,符合题意;
D、,,,根据SSS即可推出,选项说法正确,符合题意;
故选A.
【点睛】本题考查了全等三角形的判定,解题的关键是掌握全等三角形的判定.
3.C
【分析】先由∠1=∠2得到∠CAB=∠DAE,然后分别利用“SAS”、“ASA”和“AAS”对各添加的条件进行判断.
【详解】解:∵∠1=∠2,
∴∠CAB=∠DAE,
∵AC=AD,
∴①当AB=AE时,可根据“SAS”判断△ABC≌△AED;
②当BC=ED时,不能判断△ABC≌△AED;
③当∠C=∠D时,可根据“ASA”判断△ABC≌△AED;
④当∠B=∠E时,可根据“AAS”判断△ABC≌△AED.
故选:C.
【点睛】本题考查了全等三角形的判定:三条边分别对应相等的两个三角形全等;两边及其夹角分别对应相等的两个三角形全等;两角及其夹边分别对应相等的两个三角形全等;两角及其中一个角的对边对应相等的两个三角形全等.
4.C
【分析】根据折叠的性质与矩形的性质得到DC=DE=4,CP=EP,,再由三角形全等的判定定理与性质可得OE=OB,EF=BP,从而有BF=EP=CP,设BF=EP=CP=x,可得用x表示的AF、DF的长,再有勾股定理求得x的值从而得到DF的长.
【详解】解:由矩形的性质得到:DC=AB=4,AD=BC=3,,
由折叠的性质,得:DC=DE=4,CP=EP,,
在中,
,
,
∴BF=EP=CP
设BF=EP=CP=x,
则AF=4-x,BP=EF=3-x,DF=DE-EF=4-(3-x)=x+1,
在中, ,
即,
,
【点睛】本题考查了矩形得性质,折叠的性质,三角形的判定定理与性质,勾股定理等性质,利用三角形全等的判定定理与性质与线段的和差求出BF=EP=CP是关键.
5.A
【分析】根据全等三角形的判定方法及“HL”定理,判断即可.
【详解】解:①有斜边和一个锐角对应相等,可以利用AAS证明全等,故①正确;
②有斜边和一条直角边对应相等,可以利用HL证明全等,故②正确;
③有两条边相等,没有表明是对应边相等,不一定可以利用HL或SAS证明全等,故③错误;
④有两个锐角对应相等,不能利用AAA证明全等,故④错误;
综上分析可知①②正确,故A正确.
故选:A.
【点睛】本题主要考查了直角三角形全等的判定,一般三角形全等的判定方法都适合它,同时,直角三角形有它的特殊性,作为“HL”定理就是直角三角形独有的判定方法,使用时应该抓住“直角”这个隐含的已知条件.
6.B
【分析】连接NC,MC,根据SSS证△ONC≌△OMC,即可推出答案.
【详解】解:连接NC,MC,
在△ONC和△OMC中
∵,
∴△ONC≌△OMC(SSS),
∴∠AOC=∠BOC,
故选:B.
【点睛】本题考查了全等三角形的性质和判定的应用,熟练掌握三角形全等的判定是解题的关键.
7.D
【分析】求出BC=EF,再根据全等三角形的判定定理逐个判断即可.
【详解】解:∵BE=CF,
∴BE+EC=CF+EC,
即BC=EF,
A.∠A=∠D,∠B=∠DEF,BC=EF,符合全等三角形的判定定理AAS,能推出△ABC≌△DEF,故本选项不符合题意;
B.AB=DE,∠B=∠DEF,BC=EF,符合全等三角形的判定定理SAS,能推出△ABC≌△DEF,故本选项不符合题意;
C.∵AC∥DF,∴∠ACB=∠F,
∠B=∠DEF,BC=EF,∠ACB=∠F,符合全等三角形的判定定理ASA,能推出△ABC≌△DEF,故本选项不符合题意;
D.AC=DF,BC=EF,∠B=∠DEF,不符合全等三角形的判定定理,不能推出△ABC≌△DEF,故本选项符合题意;
故选:D.
【点睛】本题考查了全等三角形的判定定理,能熟记全等三角形的判定定理是解此题的关键,注意:全等三角形的判定定理有SAS,ASA,AAS,SSS,两直角三角形全等还有HL等.
8.B
【分析】根据全等三角形的判定,即可求解.
【详解】解:根据题意得:AE=AD,∠A=∠A,
A、添加AB=AC,可利用SAS判定 △ACD≌△ABE,故本选项不符合题意;
B、添加BE=DC,不能判定 △ACD≌△ABE,故本选项不符合题意;
C、添加∠B=∠C,可利用AAS判定 △ACD≌△ABE,故本选项不符合题意;
D、添加∠AEB=∠ADC,可利用ASA判定 △ACD≌△ABE,故本选项不符合题意;
故选:B
【点睛】本题主要考查了全等三角形的判定,熟练掌握全等三角形的判定是解题的关键.
9.∠A=∠D(答案不唯一)
【分析】根据平行线的性质可得∠B=∠E,又因为AB=DE,然后再利用全等三角形的判定方法即可解答.
【详解】解:∵ABED,
∴∠B=∠E,
∵AB=DE,
可添加的一个条件∠A=∠D,
∴△ABC≌△DEF(ASA),
故答案为:∠A=∠D(答案不唯一).
【点睛】本题考查了全等三角形的判定,熟练掌握全等三角形的判定定理是解题的关键.
10.12
【分析】用AAS证明△ABD≌△CAE,得AD=CE,BD=AE,得到DE=BD+CE=7+5=12cm.
【详解】∵∠BAC=90°,∠ADB=∠AEC=90°,
∴∠BAD+∠EAC=90°,∠BAD+∠ABD=90°,
∴∠EAC=∠ABD,
∵AB=AC,
∴△ABD≌△CAE(AAS),
∴AD=CE,BD=AE,
∴DE=AD+AE=CE+BD=12cm.
故答案为:12.
【点睛】本题主要考查了三角形全等,解决问题的关键是熟练掌握三角形全等的判定和性质.
11.0,3,9,12
【分析】首先分两种情况:当E在线段AB上和当E在BN上,然后再分成两种情况:AC=BE和AB=EB,分别进行计算,即可得出结果.
【详解】解:①当E在线段AB上,AC=BE时,△ACB≌△BED,
∵AC=6米,
∴BE=6米,
∴AE=12﹣6=6米,
∴点E的运动时间为6÷2=3(秒);
②当E在BN上,AC=BE时,△ACB≌△BED,
∵AC=6米,
∴BE=6米,
∴AE=12+6=18米,
∴点E的运动时间为18÷2=9(秒);
③当E在线段AB上,AB=EB时,△ACB≌△BDE,
这时E在A点未动,因此时间为0秒;
④当E在BN上,AB=EB时,△ACB≌△BDE,
∵AB=12米,
∴BE=12米,
∴AE=12+12=24米,
∴点E的运动时间为24÷2=12(秒),
故答案为:0,3,9,12.
【点睛】本题考查了全等三角形的综合问题,解本题的关键在找到所有符合题意的情况.
12.AD=CB(答案不唯一)
【分析】根据垂直定义得出∠ABD=∠CDB=90°,根据图形可知BD是公共直角边,根据直角三角形全等的判定HL得出需要添加的条件是斜边相等.
【详解】解:需要添加的条件是AD=CB.
理由是:∵AB⊥BD,CD⊥BD,
∴∠ABD=∠CDB=90°.
在Rt△ABD和Rt△CDB中,
,
∴Rt△ABD≌Rt△CDB(HL),
故答案为:AD=CB.
【点睛】本题考查了直角三角形全等的判定定理的应用,能熟记全等三角形的判定定理是解此题的关键.
13.AB=DC(答案不唯一)
【分析】根据直角三角形全等的判定方法,即可解答.
【详解】解:∵∠A=∠D=90°,BC=BC,
∴再添加:AB=DC,Rt△ABC≌Rt△DCB(HL);
∵∠A=∠D=90°,BC=BC,
∴再添加:AC=BD,Rt△ABC≌Rt△DCB(HL);
∵∠A=∠D=90°,BC=BC,
∴再添加:∠ABC=∠DCB,Rt△ABC≌Rt△DCB(AAS);
∵∠A=∠D=90°,BC=BC,
∴再添加:∠ACB=∠DBC,Rt△ABC≌Rt△DCB(AAS);
故答案为:AB=DC(答案不唯一) .
【点睛】本题考查了直角三角形全等的判定,熟练掌握直角三角形全等的判定方法是解题的关键.
14.61
【分析】由“HL”可证Rt△ABE≌Rt△CBF,可得∠BAE=∠BCF=16°,即可求解.
【详解】解:∵在△ABC中,∠ABC=90°,AB=CB,
∴∠BAC=∠BCA=45°,
∵∠CAE=29°,
∴∠BAE=16°,
在Rt△ABE和Rt△CBF中,,
∴Rt△ABE≌Rt△CBF(HL),
∴∠BAE=∠BCF=16°,
∴∠ACF=∠BCA+∠BCF=61°,
故答案为:61.
【点睛】本题考查了全等三角形的判定和性质,证明Rt△ABE≌Rt△CBF是本题的关键.
15.HL
【分析】根据HL证明Rt△AOE≌Rt△AOF即可.
【详解】解:∵OE⊥AB,OF⊥AC,
∴∠AEO=∠AFO=90°,
在Rt△AOE和Rt△AOF中,
∴Rt△AOE≌Rt△AOF(HL).
故答案为HL.
【点睛】本题考查全等三角形的判定,解题的关键是熟练掌握基本知识,属于中考常考题型.
16.2.5
【分析】根据平行线性质得出∠ADE=∠F,∠FCE=∠A,求出AE= EC,根据AAS证△ADE≌△CFE,根据全等三角形的性质推出即可.
【详解】证明:∵CF//AB,
∴∠ADE=∠F,∠FCE=∠A,
∵点E为AC的中点,
∴AE= EC,
在△ADE和 CFE中,
∴△ADE≌ CFE(AAS),
∴AD= CF= 6.5,
∵AB= 9,
∴BD= AB- AD=9- 6.5= 2.5,
故答案为: 2.5.
【点睛】本题考查了全等三角形的性质和判定,平行线的性质,注意:全等三角形的对应边相等,全等三角形的判定定理有SAS,ASA, AAS,SSS.
17.BD=BE.理由见解析
【分析】首先根据垂直的定义,得出∠C=∠A=90°,再根据,判定出△ABE≌△CDB,然后再根据全等三角形的性质,得出BD=BE.
【详解】解:BD=BE.理由如下:
∵DC⊥CA,EA⊥CA,
∴∠C=∠A=90°,
∵在△ABE和△CDB中
AB=CD,∠A=∠C,AE=CB,
∴△ABE≌△CDB(SAS),
∴BD=BE.
【点睛】本题考查了全等三角形的性质与判定、垂直的定义,解本题的关键在熟练掌握全等三角形的判定定理.判定全等三角形的方法有.
18.见解析
【分析】由垂直的定义可得,由可得,再证,,由全等三角形的对应边相等即可得证.
【详解】证明:∵,,
∴,
∵,
∴,
又∵,
∴,
∴,
∵,,
∴,
∴.
【点睛】本题考查了全等三角形的判定与性质,证明三角形全等是解题的关键.
19.见解析
【分析】证△ABE≌△ACD,推出∠B=∠C,AD=AE,求出BD=CE,证△BDO≌△CEO,根据全等三角形的性质推出即可.
【详解】证明:∵BE⊥AC,CD⊥AB,
∴∠ADC=∠AEB=90°,
在△ABE和△ACD中
∴△ABE≌△ACD (AAS),
∴∠B=∠C,AD=AE,
∵AB=AC,
∴BD=CE,
在△BDO和△CEO中
∴△BDO≌△CEO (AAS),
∴OB=OC.
【点睛】本题考查了全等三角形的性质和判定的应用,主要考查学生的推理能力.
20.∠3=45°
【分析】根据等式的性质得出∠BAD=∠CAE,再利用全等三角形的判定和性质解答即可.
【详解】解:∵∠BAC=∠DAE,
∴∠BAC-∠DAC=∠DAE-∠DAC,
即∠BAD=∠CAE,
在△BAD与△CAE中,
,
∴△BAD≌△CAE(SAS),
∴∠ABD=∠2=25°,
∴∠3=∠1+∠ABD=25°+20°=45°.
【点睛】此题考查全等三角形的判定和性质,三角形的外角性质,关键是根据等式的性质得出∠BAD=∠CAE.
答案第1页,共2页
答案第10页,共10页
一、单选题
1.如图,甲、乙、丙三个三角形和左侧△ABC全等的是( )
A.甲和乙 B.甲和丙 C.乙和丙 D.只有丙
2.下列条件,不能判定的是( )
A.,, B.,,
C.,, D.,,
3.如图,已知∠1=∠2,AC=AD,增加下列条件之一:①AB=AE;②BC=ED;③∠C=∠D;④∠B=∠E.其中能使△ABC≌△AED的条件有( )
A.1个 B.2个 C.3个 D.4个
4.如图,已知矩形纸片,,,点在边上,将沿折叠,点落在点处,,分别交于点,,且,则的长为( )
A. B. C. D.
5.两个直角三角形中:①一锐角和斜边对应相等;②斜边和一直角边对应相等;③有两条边相等;④两个锐角对应相等.能使这两个直角三角形全等的是( )
A.①② B.②③ C.③④ D.①②③④
6.用直尺和圆规作一个角的平分线的示意图如图所示,则能说明∠AOC=∠BOC的依据是( )
A.全等三角形的定义 B.SSS C.ASA D.AAS
7.如图,点B、E、C、F四点共线,∠B =∠DEF,BE = CF,添加一个条件,不能判定 △ABC ≌ △DEF的是( )
A.∠A=∠D B.AB=DE C.AC∥DF D.AC=DF
8.如图,已知AE=AD,添加下列条件不能判定 △ACD≌△ABE的是( )
A.AB=AC B.BE=DC C.∠B=∠C D.∠AEB=∠ADC
二、填空题
9.如图,点B、F、C、E在一条直线上,ABED, AB=DE,要使△ABC≌△DEF,可以添加的一个条件是:________.
10.如图,在Rt△ABC中,∠BAC=90°,AB=AC,分别过点B,C作过点A的直线的垂线BD,CE,若BD=7cm,CE=5cm,则DE=________cm.
11.如图,CA⊥AB,垂足为点A,AB=12米,AC=6米,射线BM⊥AB,垂足为点B,动点E从A点出发以2米/秒沿射线AN运动,点D为射线BM上一动点,随着E点运动而运动,且始终保持ED=CB,当点E经过_____时,由点D、E、B组成的三角形与△BCA全等.
12.如图,已知AB⊥BD,CD⊥BD,若用“HL”判定Rt△ABD和Rt△CDB全等,则需要添加的条件是______.
13.如图,在RtABC与RtDCB中,已知∠A=∠D=90°,为了使RtABC≌RtDCB,需添加的条件是______(不添加字母和辅助线).
14.如图,在△ABC中,∠ABC=90°,AB=CB,F为AB延长线上一点,点E在BC上,且AE=CF,若∠CAE=29°,则∠ACF的度数为________°.
15.如图,O是∠BAC内一点,且点O到AB,AC的距离OE,OF相等,则△AEO≌△AFO的依据是_____.
16.如图,E是的边的中点,过点C作,过点E作直线交于D,交于F,若,则的长为__________.
三、解答题
17.已知:如图DC⊥CA,EA⊥CA,CD=AB,CB=AE,那么BD=BE吗?试说明理由.
18.如图,点E、C、F、B在一条直线上,,,,,AD交BE于O;
求证:.
19.如图,AB=AC,BE⊥AC于E,CD⊥AB于D,BE、CD交于点O,求证:OB=OC.
20.如图所示,D在线段BE上,AB=AC,AD=AE,∠BAC=∠DAE,∠1=20°,∠2=25°,求∠3的度数.
试卷第1页,共3页
参考答案:
1.C
【分析】根据三角形全等的判定方法得出乙和丙与△ABC全等,甲与△ABC不全等.
【详解】解:在△ABC和乙的三角形中,两边及其夹角对应相等,满足三角形全等的判定方法:SAS,
所以乙和△ABC全等;
在△ABC和丙的三角形中,两个及一角对边对应相等,满足三角形全等的判定方法:AAS,
所以丙和△ABC全等;
在△ABC和甲的三角形中,只有一边一角对应相等南,不能判定甲与△ABC全等;
故选:C.
【点睛】本题考查了三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.
2.A
【分析】根据全等三角形的判定SSS,AAS,ASA,SAS,进行判断即可得.
【详解】解:A、∠A=∠A′,AB=A′B′,,根据SSA不能推出,选项说法错误,不符合题意;
B、,,,根据ASA即可推出,选项说法正确,符合题意;
C、,,,根据AAS即可推出,选项说法正确,符合题意;
D、,,,根据SSS即可推出,选项说法正确,符合题意;
故选A.
【点睛】本题考查了全等三角形的判定,解题的关键是掌握全等三角形的判定.
3.C
【分析】先由∠1=∠2得到∠CAB=∠DAE,然后分别利用“SAS”、“ASA”和“AAS”对各添加的条件进行判断.
【详解】解:∵∠1=∠2,
∴∠CAB=∠DAE,
∵AC=AD,
∴①当AB=AE时,可根据“SAS”判断△ABC≌△AED;
②当BC=ED时,不能判断△ABC≌△AED;
③当∠C=∠D时,可根据“ASA”判断△ABC≌△AED;
④当∠B=∠E时,可根据“AAS”判断△ABC≌△AED.
故选:C.
【点睛】本题考查了全等三角形的判定:三条边分别对应相等的两个三角形全等;两边及其夹角分别对应相等的两个三角形全等;两角及其夹边分别对应相等的两个三角形全等;两角及其中一个角的对边对应相等的两个三角形全等.
4.C
【分析】根据折叠的性质与矩形的性质得到DC=DE=4,CP=EP,,再由三角形全等的判定定理与性质可得OE=OB,EF=BP,从而有BF=EP=CP,设BF=EP=CP=x,可得用x表示的AF、DF的长,再有勾股定理求得x的值从而得到DF的长.
【详解】解:由矩形的性质得到:DC=AB=4,AD=BC=3,,
由折叠的性质,得:DC=DE=4,CP=EP,,
在中,
,
,
∴BF=EP=CP
设BF=EP=CP=x,
则AF=4-x,BP=EF=3-x,DF=DE-EF=4-(3-x)=x+1,
在中, ,
即,
,
【点睛】本题考查了矩形得性质,折叠的性质,三角形的判定定理与性质,勾股定理等性质,利用三角形全等的判定定理与性质与线段的和差求出BF=EP=CP是关键.
5.A
【分析】根据全等三角形的判定方法及“HL”定理,判断即可.
【详解】解:①有斜边和一个锐角对应相等,可以利用AAS证明全等,故①正确;
②有斜边和一条直角边对应相等,可以利用HL证明全等,故②正确;
③有两条边相等,没有表明是对应边相等,不一定可以利用HL或SAS证明全等,故③错误;
④有两个锐角对应相等,不能利用AAA证明全等,故④错误;
综上分析可知①②正确,故A正确.
故选:A.
【点睛】本题主要考查了直角三角形全等的判定,一般三角形全等的判定方法都适合它,同时,直角三角形有它的特殊性,作为“HL”定理就是直角三角形独有的判定方法,使用时应该抓住“直角”这个隐含的已知条件.
6.B
【分析】连接NC,MC,根据SSS证△ONC≌△OMC,即可推出答案.
【详解】解:连接NC,MC,
在△ONC和△OMC中
∵,
∴△ONC≌△OMC(SSS),
∴∠AOC=∠BOC,
故选:B.
【点睛】本题考查了全等三角形的性质和判定的应用,熟练掌握三角形全等的判定是解题的关键.
7.D
【分析】求出BC=EF,再根据全等三角形的判定定理逐个判断即可.
【详解】解:∵BE=CF,
∴BE+EC=CF+EC,
即BC=EF,
A.∠A=∠D,∠B=∠DEF,BC=EF,符合全等三角形的判定定理AAS,能推出△ABC≌△DEF,故本选项不符合题意;
B.AB=DE,∠B=∠DEF,BC=EF,符合全等三角形的判定定理SAS,能推出△ABC≌△DEF,故本选项不符合题意;
C.∵AC∥DF,∴∠ACB=∠F,
∠B=∠DEF,BC=EF,∠ACB=∠F,符合全等三角形的判定定理ASA,能推出△ABC≌△DEF,故本选项不符合题意;
D.AC=DF,BC=EF,∠B=∠DEF,不符合全等三角形的判定定理,不能推出△ABC≌△DEF,故本选项符合题意;
故选:D.
【点睛】本题考查了全等三角形的判定定理,能熟记全等三角形的判定定理是解此题的关键,注意:全等三角形的判定定理有SAS,ASA,AAS,SSS,两直角三角形全等还有HL等.
8.B
【分析】根据全等三角形的判定,即可求解.
【详解】解:根据题意得:AE=AD,∠A=∠A,
A、添加AB=AC,可利用SAS判定 △ACD≌△ABE,故本选项不符合题意;
B、添加BE=DC,不能判定 △ACD≌△ABE,故本选项不符合题意;
C、添加∠B=∠C,可利用AAS判定 △ACD≌△ABE,故本选项不符合题意;
D、添加∠AEB=∠ADC,可利用ASA判定 △ACD≌△ABE,故本选项不符合题意;
故选:B
【点睛】本题主要考查了全等三角形的判定,熟练掌握全等三角形的判定是解题的关键.
9.∠A=∠D(答案不唯一)
【分析】根据平行线的性质可得∠B=∠E,又因为AB=DE,然后再利用全等三角形的判定方法即可解答.
【详解】解:∵ABED,
∴∠B=∠E,
∵AB=DE,
可添加的一个条件∠A=∠D,
∴△ABC≌△DEF(ASA),
故答案为:∠A=∠D(答案不唯一).
【点睛】本题考查了全等三角形的判定,熟练掌握全等三角形的判定定理是解题的关键.
10.12
【分析】用AAS证明△ABD≌△CAE,得AD=CE,BD=AE,得到DE=BD+CE=7+5=12cm.
【详解】∵∠BAC=90°,∠ADB=∠AEC=90°,
∴∠BAD+∠EAC=90°,∠BAD+∠ABD=90°,
∴∠EAC=∠ABD,
∵AB=AC,
∴△ABD≌△CAE(AAS),
∴AD=CE,BD=AE,
∴DE=AD+AE=CE+BD=12cm.
故答案为:12.
【点睛】本题主要考查了三角形全等,解决问题的关键是熟练掌握三角形全等的判定和性质.
11.0,3,9,12
【分析】首先分两种情况:当E在线段AB上和当E在BN上,然后再分成两种情况:AC=BE和AB=EB,分别进行计算,即可得出结果.
【详解】解:①当E在线段AB上,AC=BE时,△ACB≌△BED,
∵AC=6米,
∴BE=6米,
∴AE=12﹣6=6米,
∴点E的运动时间为6÷2=3(秒);
②当E在BN上,AC=BE时,△ACB≌△BED,
∵AC=6米,
∴BE=6米,
∴AE=12+6=18米,
∴点E的运动时间为18÷2=9(秒);
③当E在线段AB上,AB=EB时,△ACB≌△BDE,
这时E在A点未动,因此时间为0秒;
④当E在BN上,AB=EB时,△ACB≌△BDE,
∵AB=12米,
∴BE=12米,
∴AE=12+12=24米,
∴点E的运动时间为24÷2=12(秒),
故答案为:0,3,9,12.
【点睛】本题考查了全等三角形的综合问题,解本题的关键在找到所有符合题意的情况.
12.AD=CB(答案不唯一)
【分析】根据垂直定义得出∠ABD=∠CDB=90°,根据图形可知BD是公共直角边,根据直角三角形全等的判定HL得出需要添加的条件是斜边相等.
【详解】解:需要添加的条件是AD=CB.
理由是:∵AB⊥BD,CD⊥BD,
∴∠ABD=∠CDB=90°.
在Rt△ABD和Rt△CDB中,
,
∴Rt△ABD≌Rt△CDB(HL),
故答案为:AD=CB.
【点睛】本题考查了直角三角形全等的判定定理的应用,能熟记全等三角形的判定定理是解此题的关键.
13.AB=DC(答案不唯一)
【分析】根据直角三角形全等的判定方法,即可解答.
【详解】解:∵∠A=∠D=90°,BC=BC,
∴再添加:AB=DC,Rt△ABC≌Rt△DCB(HL);
∵∠A=∠D=90°,BC=BC,
∴再添加:AC=BD,Rt△ABC≌Rt△DCB(HL);
∵∠A=∠D=90°,BC=BC,
∴再添加:∠ABC=∠DCB,Rt△ABC≌Rt△DCB(AAS);
∵∠A=∠D=90°,BC=BC,
∴再添加:∠ACB=∠DBC,Rt△ABC≌Rt△DCB(AAS);
故答案为:AB=DC(答案不唯一) .
【点睛】本题考查了直角三角形全等的判定,熟练掌握直角三角形全等的判定方法是解题的关键.
14.61
【分析】由“HL”可证Rt△ABE≌Rt△CBF,可得∠BAE=∠BCF=16°,即可求解.
【详解】解:∵在△ABC中,∠ABC=90°,AB=CB,
∴∠BAC=∠BCA=45°,
∵∠CAE=29°,
∴∠BAE=16°,
在Rt△ABE和Rt△CBF中,,
∴Rt△ABE≌Rt△CBF(HL),
∴∠BAE=∠BCF=16°,
∴∠ACF=∠BCA+∠BCF=61°,
故答案为:61.
【点睛】本题考查了全等三角形的判定和性质,证明Rt△ABE≌Rt△CBF是本题的关键.
15.HL
【分析】根据HL证明Rt△AOE≌Rt△AOF即可.
【详解】解:∵OE⊥AB,OF⊥AC,
∴∠AEO=∠AFO=90°,
在Rt△AOE和Rt△AOF中,
∴Rt△AOE≌Rt△AOF(HL).
故答案为HL.
【点睛】本题考查全等三角形的判定,解题的关键是熟练掌握基本知识,属于中考常考题型.
16.2.5
【分析】根据平行线性质得出∠ADE=∠F,∠FCE=∠A,求出AE= EC,根据AAS证△ADE≌△CFE,根据全等三角形的性质推出即可.
【详解】证明:∵CF//AB,
∴∠ADE=∠F,∠FCE=∠A,
∵点E为AC的中点,
∴AE= EC,
在△ADE和 CFE中,
∴△ADE≌ CFE(AAS),
∴AD= CF= 6.5,
∵AB= 9,
∴BD= AB- AD=9- 6.5= 2.5,
故答案为: 2.5.
【点睛】本题考查了全等三角形的性质和判定,平行线的性质,注意:全等三角形的对应边相等,全等三角形的判定定理有SAS,ASA, AAS,SSS.
17.BD=BE.理由见解析
【分析】首先根据垂直的定义,得出∠C=∠A=90°,再根据,判定出△ABE≌△CDB,然后再根据全等三角形的性质,得出BD=BE.
【详解】解:BD=BE.理由如下:
∵DC⊥CA,EA⊥CA,
∴∠C=∠A=90°,
∵在△ABE和△CDB中
AB=CD,∠A=∠C,AE=CB,
∴△ABE≌△CDB(SAS),
∴BD=BE.
【点睛】本题考查了全等三角形的性质与判定、垂直的定义,解本题的关键在熟练掌握全等三角形的判定定理.判定全等三角形的方法有.
18.见解析
【分析】由垂直的定义可得,由可得,再证,,由全等三角形的对应边相等即可得证.
【详解】证明:∵,,
∴,
∵,
∴,
又∵,
∴,
∴,
∵,,
∴,
∴.
【点睛】本题考查了全等三角形的判定与性质,证明三角形全等是解题的关键.
19.见解析
【分析】证△ABE≌△ACD,推出∠B=∠C,AD=AE,求出BD=CE,证△BDO≌△CEO,根据全等三角形的性质推出即可.
【详解】证明:∵BE⊥AC,CD⊥AB,
∴∠ADC=∠AEB=90°,
在△ABE和△ACD中
∴△ABE≌△ACD (AAS),
∴∠B=∠C,AD=AE,
∵AB=AC,
∴BD=CE,
在△BDO和△CEO中
∴△BDO≌△CEO (AAS),
∴OB=OC.
【点睛】本题考查了全等三角形的性质和判定的应用,主要考查学生的推理能力.
20.∠3=45°
【分析】根据等式的性质得出∠BAD=∠CAE,再利用全等三角形的判定和性质解答即可.
【详解】解:∵∠BAC=∠DAE,
∴∠BAC-∠DAC=∠DAE-∠DAC,
即∠BAD=∠CAE,
在△BAD与△CAE中,
,
∴△BAD≌△CAE(SAS),
∴∠ABD=∠2=25°,
∴∠3=∠1+∠ABD=25°+20°=45°.
【点睛】此题考查全等三角形的判定和性质,三角形的外角性质,关键是根据等式的性质得出∠BAD=∠CAE.
答案第1页,共2页
答案第10页,共10页
