椭圆及其标准方程(1)[上学期]
文档属性
| 名称 | 椭圆及其标准方程(1)[上学期] |  | |
| 格式 | rar | ||
| 文件大小 | 101.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-03-17 22:10:00 | ||
图片预览






文档简介
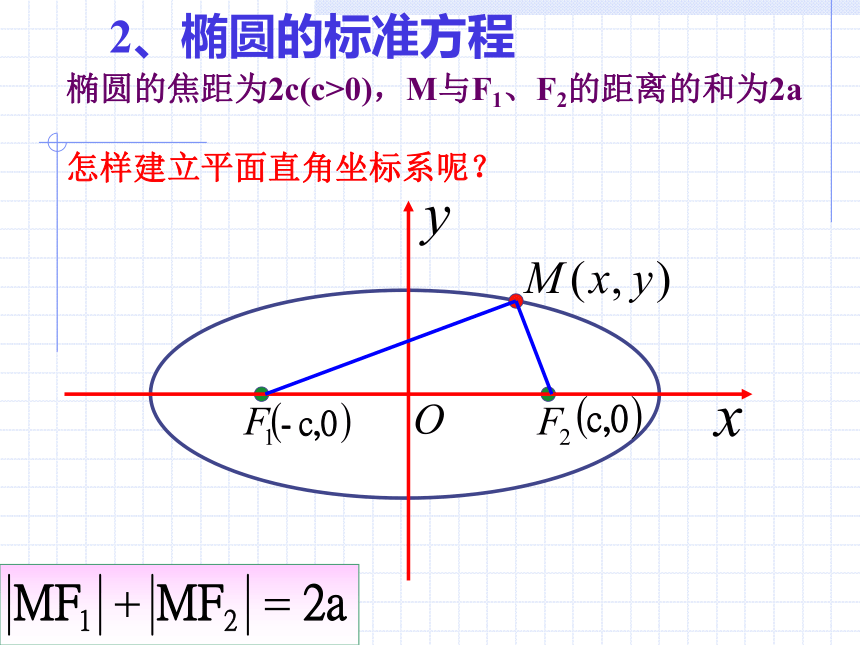
课件15张PPT。椭圆及其标准方程演示2演示11、椭圆的定义: 平面内到两个定点F1、F2的距离之和等于常数(大于|F1F2|)的点的轨迹叫做椭圆。 这两个定点叫做椭圆的焦点,两焦点间的距离叫做椭圆的焦距。几点说明:1、F1、F2是两个不同的定点;2、M是椭圆上任意一点,且|MF1| + |MF2| = 常数;3、通常这个常数记为2a,焦距记为2c,且2a>2c(?);4、如果2a = 2c,则M点的轨迹是线段F1F2.5、如果2a < 2c,则M点的轨迹不存在.(由三角形的性质知) 下面我们来求椭圆的标准方程.2、椭圆的标准方程 求曲线方程的方法步骤是什么?怎样建立平面直角坐标系呢?2、椭圆的标准方程椭圆的焦距为2c(c>0),M与F1、F2的距离的和为2a2、椭圆的标准方程 取过焦点F1、F2的直线为x轴,线段F1F2的垂直平分线为y轴,建立直角坐标系。 设M(x,y)是椭圆上任一点,椭圆的焦距为2c(c>0),M与F1、F2的距离的和等于正常数2a,则F1(-c,0)、F2(c,0)。, (1)两边平方得叫做椭圆的标准方程,焦点在x 轴上。定 义图 形方 程焦 点F(±c,0)F(0,±c)a,b,c之间的关系c2=a2-b2|MF1|+|MF2|=2a (2a>2c>0)椭圆的标准方程例1、填空:
(1)已知椭圆的方程为: ,则a=_____,b=_______,c=_______,焦点坐标为:____________焦距等于______;若CD为过左焦点F1的弦,则△F2CD的周长为________543(3,0)、(-3,0)620F1F2CD例题讲解(2)已知椭圆的方程为: ,则a=_____,b=_______,c=_______,焦点坐标为:___________焦距等于__________;曲线上一点P到焦点F1的距离为3,则点P到另一个焦点F2的距离等于_________,则△F1PF2的周长为___________21(0,-1)、(0,1)2例2、求满足下列条件的椭圆的标准方程:(1)满足a=4,b=1,焦点在X轴上的椭圆的标准方程为____________ (2)满足a=4,c= ,焦点在Y轴上的椭圆的标准方程为____________两个焦点的坐标分别是(0,-2)、(0,2),并且椭圆经过点解:∵ 椭圆的焦点在y轴上,由椭圆的定义知,例3:求适合下列条件的椭圆的标准方程:∴ 设它的标准方程为又 ∵ c=2∴ 所求的椭圆的标准方程为求椭圆的标准方程
(1)首先要判断类型,
(2)用待定系数法求一、二、二一个概念;二个方程;小结二个方法:例4:化简:OXYF1F2M(0,-3)(0 , 3)(x,y)答案:|MF1|+ |MF2|=10分析:点M(x,y)到两定点(0,-3)、(0,3)的距离之和为定值10。作业1、课本53页A组第2题
(1)已知椭圆的方程为: ,则a=_____,b=_______,c=_______,焦点坐标为:____________焦距等于______;若CD为过左焦点F1的弦,则△F2CD的周长为________543(3,0)、(-3,0)620F1F2CD例题讲解(2)已知椭圆的方程为: ,则a=_____,b=_______,c=_______,焦点坐标为:___________焦距等于__________;曲线上一点P到焦点F1的距离为3,则点P到另一个焦点F2的距离等于_________,则△F1PF2的周长为___________21(0,-1)、(0,1)2例2、求满足下列条件的椭圆的标准方程:(1)满足a=4,b=1,焦点在X轴上的椭圆的标准方程为____________ (2)满足a=4,c= ,焦点在Y轴上的椭圆的标准方程为____________两个焦点的坐标分别是(0,-2)、(0,2),并且椭圆经过点解:∵ 椭圆的焦点在y轴上,由椭圆的定义知,例3:求适合下列条件的椭圆的标准方程:∴ 设它的标准方程为又 ∵ c=2∴ 所求的椭圆的标准方程为求椭圆的标准方程
(1)首先要判断类型,
(2)用待定系数法求一、二、二一个概念;二个方程;小结二个方法:例4:化简:OXYF1F2M(0,-3)(0 , 3)(x,y)答案:|MF1|+ |MF2|=10分析:点M(x,y)到两定点(0,-3)、(0,3)的距离之和为定值10。作业1、课本53页A组第2题
