数学苏教版(2019)必修第一册8.1.1 函数的零点 同步练习(Word版含答案)
文档属性
| 名称 | 数学苏教版(2019)必修第一册8.1.1 函数的零点 同步练习(Word版含答案) | 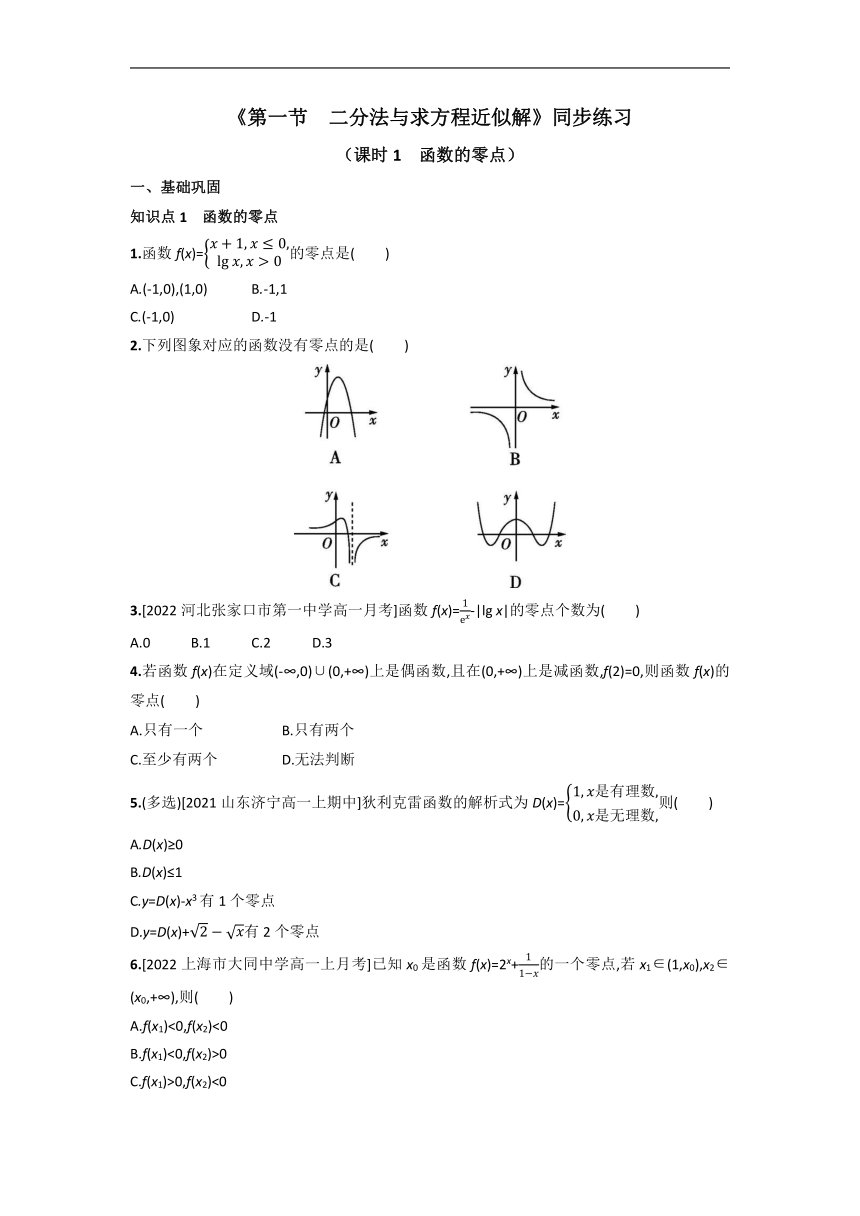 | |
| 格式 | docx | ||
| 文件大小 | 96.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-22 05:13:43 | ||
图片预览




文档简介
《第一节 二分法与求方程近似解》同步练习
(课时1 函数的零点)
一、基础巩固
知识点1 函数的零点
1.函数f(x)=的零点是( )
A.(-1,0),(1,0) B.-1,1
C.(-1,0) D.-1
2.下列图象对应的函数没有零点的是( )
3.[2022河北张家口市第一中学高一月考]函数f(x)=-|lg x|的零点个数为( )
A.0 B.1 C.2 D.3
4.若函数f(x)在定义域(-∞,0)∪(0,+∞)上是偶函数,且在(0,+∞)上是减函数,f(2)=0,则函数f(x)的零点( )
A.只有一个 B.只有两个
C.至少有两个 D.无法判断
5.(多选)[2021山东济宁高一上期中]狄利克雷函数的解析式为D(x)=则( )
A.D(x)≥0
B.D(x)≤1
C.y=D(x)-x3有1个零点
D.y=D(x)+有2个零点
6.[2022上海市大同中学高一上月考]已知x0是函数f(x)=2x+的一个零点,若x1∈(1,x0),x2∈(x0,+∞),则( )
A.f(x1)<0,f(x2)<0
B.f(x1)<0,f(x2)>0
C.f(x1)>0,f(x2)<0
D.f(x1)>0,f(x2)>0
7.[2022广东阳春二中高一上月考]若是函数f(x)=2x2-ax+3的一个零点,则f(x)的另一个零点为 .
知识点2 函数零点存在定理
8.(多选)[2022江苏海安高一上期末]已知函数y=f(x)的图象在区间[0,1]上是一条连续不断的曲线,则下列结论正确的是( )
A.若f(0)f(1)<0,则y=f(x)在(0,1)内至少有一个零点
B.若f(0)f(1)>0,则y= f(x)在(0,1)内没有零点
C.若y=f(x)在(0,1)内没有零点,则必有f(0)f(1)≥0
D.若y=f(x)在(0,1)内有唯一零点,且f(0)f(1)<0,则f(x)在(0,1)上是单调函数
9.[2022江苏淮安高一上期末]已知f(x),g(x)均为[-1,3]上连续不断的曲线,根据下表能判断方程f(x)=g(x)有实数解的区间是( )
x -1 0 1 2 3
f(x) -0.670 3.011 5.432 5.980 7.651
g(x) -0.530 3.451 4.890 5.241 6.892
A.(-1,0) B.(0,1)
C.(1,2) D.(2,3)
10.[2022江苏宿迁高一期末]设方程2x+2x=10的根为β,则β属于( )
A.(0,1) B.(1,2)
C.(2,3) D.(3,4)
11.(多选)已知函数f(x)=ex-x-2,则下列区间中含f(x)的零点的是( )
A.(-2,-1) B.(-1,0)
C.(0,1) D.(1,2)
12.若aA.(a,b)和(b,c)内
B.(-∞,a)和(a,b)内
C.(b,c)和(c,+∞)内
D.(-∞,a)和(c,+∞)内
13.求证:方程3x=在(0,1)内必有一个实数根.
知识点3 函数的零点的应用
14.已知函数f(x)=2x+x-10的零点x0∈(k,k+1),其中k为整数,则k的值为( )
A.0 B.1 C.2 D.3
15.(多选)[2022江苏省太湖高级中学高二下月考]函数f(x)=2x--a的一个零点在区间(1,2)内,则实数a的可能取值是( )
A.0 B.1 C.2 D.3
16.[2022天津和平区高一上期末]已知函数f(x)=a|x|+m-1(0A.(-∞,0) B.(-∞,0]
C.[0,1) D.[1,2)
17.[2022广东普宁华侨中学高一下月考]已知函数f(x)=若函数g(x)=f(x)-t(t∈R)有3个不同的零点a,b,c,则2a+2b+2c的取值范围是( )
A.[16,32] B.[16,34)
C.(18,32] D.(18,34)
18.[2022上海建平中学高一下月考]设ω>0,若函数y=sin ωx在区间[0,2π]上恰有两个零点,则ω的取值范围为 .
19.已知函数f(x)=-x2+2ex+m-1,g(x)=x+(x>0).
(1)若y=g(x)-m有零点,求实数m的取值范围;
(2)若g(x)-f(x)=0有两个不相等的实根,求实数m的取值范围.
二、能力提升
1.(多选)[2022河北石家庄高一上期末]已知函数f(x)=2x+x,g(x)=log2x+x,h(x)=x3+x的零点分别为a,b,c,则( )
A.-1C.b2.(多选)[2022安徽示范高中高二上联考]已知函数f(x)是定义在R上的减函数,实数a,b,c(aA.x0C.bc
3.(多选)[2021广东珠海高一上期末]已知函数f(x)=若f(x1)=f(x2)=f(x3)=f(x4),且x1A.x1+x2=2 B.x3x4=1
C.04.[2021江苏溧阳高一上期末]对于函数f(x),g(x),设α∈{x|f(x)=0},β∈{x|g(x)=0}.若存在α,β,使得|α-β|≤2,则称f(x),g(x)互为“零点相邻函数”.若f(x)=ex-2+x-3与g(x)=x2-ax-a-2互为“零点相邻函数”,则实数a的取值范围是( )
A.(-2,)
B. [-2,]
C.(-∞,-2)∪(,+∞)
D.(-∞,-2]∪[,+∞)
5.[2022北京房山区高三一模]函数f(x)的图象在区间(0,2)上连续不断,写出一个能说明“若f(x)在区间(0,2)上存在零点,则f(0)f(2)<0”为假命题的f(x)= .
6.[2022湖北部分重点高中高一上期末]已知函数f(x)=|2-x-1|,g(x)=且方程f(x)=m有2个不同的解,则实数m的取值范围为 ,方程g(f(x))=m的解的个数为 .
7.[2022江苏镇江高一上期末]已知函数f(x)=3x+a·3-x为偶函数.
(1)求实数a的值;
(2)设函数g(x)=f(x)+x-3-x-3的零点为x0,求证:8.已知函数f(x)=+4log2x+m,x∈[,4],m为常数.
(1)若函数f(x)存在大于1的零点,求实数m的取值范围;
(2)设函数f(x)有两个互异的零点α,β,求实数m的取值范围,并求α·β的值.
参考答案
一、基础巩固
1.B 令f(x)=0,则或解得x=-1或x=1.故选B.
2.B 函数图象与x轴无交点即函数没有零点.故选B.
3.C
4.B 因为f(x)在(0,+∞)上是减函数,f(2)=0,所以f(x)在(0,+∞)上有且仅有一个零点2.又f(x)是偶函数,所以f(x)在(-∞,0)上有且仅有一个零点-2.故函数f(x)只有两个零点-2和2.
5.ABC 因为D(x)的值域为{0,1},所以A,B正确.当x是无理数时,由D(x)-x3=0,得0-x3=0,解得x=0,不合题意;当x是有理数时,由D(x)-x3=0,得1-x3=0,解得x=1.则y=D(x)-x3有1个零点,故C正确.令y=D(x)+=0,则D(x)=,当D(x)=1时, x=3+2为无理数,不合题意;当D(x)=0时,x=2为有理数,不合题意.所以y=D(x)+没有零点,故D错误.故选ABC.
6.B
7.1
8.AC
9.B 令h(x)=f(x)-g(x),由表中数据可得,h(-1)<0,h(0)<0,h(1)>0,h(2)>0,h(3)>0.根据零点存在定理,可知h(x)在(0,1)上有零点,故f(x)=g(x)在(0,1)上有实数解.
10.C 设f(x)=2x+2x-10,则f(x)在R上为增函数.又f(2)=-2,f(3)=4,f(2)f(3)<0,所以f(x)在(2,3)上有唯一实根,所以β∈(2,3).
11.AD 因为f(-2)=e-2+2-2=e-2>0,f(-1)=e-1+1-2=e-1-1<0,f(0)=e0-0-2=-1<0,f(1)=e1-1-2=e-3<0,f(2)
=e2-2-2=e2-4>0,所以根据函数零点存在定理,可知区间(-2,-1)和(1,2)中含f(x)的零点.故选AD.
12.A 由于f(a)=(a-b)(a-c)>0,f(b)=(b-c)(b-a)<0,f(c)=(c-a)(c-b)>0,因此f(x)的两个零点分别在区间(a,b)和(b,c)内,故选A.
13.证明:设函数f(x)=3x-=3x+1-.因为y=3x+1与y=-在(0,1)内均为增函数,
所以函数f(x)在(0,1)内是增函数.
又f(0)=30-2=-1<0,f(1)=3->0,即f(0)·f(1)<0,
所以函数f(x)在区间(0,1)内有零点,且只有一个,
即方程3x=在(0,1)内必有一个实数根.
14.C 易知函数f(x)在其定义域内为增函数,故f(x)至多有一个零点.因为f(2)=22+2-10=-4<0,f(3)=23+3-10=1>0,所以f(2)f(3)<0,即函数f(x)在(2,3)内存在一个零点x0.又x0∈(k,k+1),k为整数,所以k=2.
15.BC 因为函数y=2x,y=-在(0,+∞)上单调递增,所以函数f(x)在(0,+∞)上单调递增.由零点存在定理,得f(1)f(2)=-a(3-a)<0,解得016.C 因为017.D
18.[,1)
19.(1)作出g(x)=x+(x>0),y=m的大致图象,如图1所示.
由图可知若y=g(x)-m有零点,则m≥2e,
所以实数m的取值范围是[2e,+∞).
(2)g(x)-f(x)=0有两个不相等的实根,即g(x)与f(x)的图象有两个交点.
因为f(x)=-x2+2ex+m-1=-(x-e)2+m-1+e2,
所以其图象的对称轴为直线x=e,开口向下,函数f(x)的最大值为m-1+e2.
作出函数f(x)与g(x)的大致图象,如图2所示.
故当m-1+e2>2e,即m>-e2+2e+1时,g(x)与f(x)的图象有两个交点,即g(x)-f(x)=0有两个不相等的实根,
所以实数m的取值范围是(-e2+2e+1,+∞).
二、能力提升
1.AD
2.AC 因为函数f(x)是定义在R上的减函数,且af(b)>f(c).又f(a)f(b)f(c)<0,所以f(a),f(b),f(c)中有一个或三个为负.当f(a),f(b),f(c)中有一个为负时,f(a)>f(b)>0>f(c),此时b3.BCD 函数f(x)=的图象如图所示.设f(x1)=f(x2)=f(x3)=f(x4)=t,则04.B 因为f(2)=0,且f(x)在R上为增函数,所以f(x)只有唯一零点2.又f(x),g(x)互为“零点相邻函数”,所以g(x)在[0,4]上至少有一个零点.由g(x)=x2-ax-a-2=0,得a= =(x+1)--2.令t=x+1,h(t)=t--2.由0≤x≤4,得1≤t≤5.因为h(t)在[1,5]上单调递增,所以当t∈[1,5]时,h(t)∈[-2,],所以a∈[-2,].
5.(x-1)2(答案不唯一)
6.(0,1) 4
7.(1)由f(-x)=f(x),得3x+a·3-x=3-x+a·3x,所以a=1.
(2)由(1)得f(x)=3x+3-x,所以g(x)=3x+3-x+x-3-x-3=3x+x-3.
因为函数g(x)在R上单调递增,且g(log32)=2+log32-3<0,g(log32.5)=2.5+log32.5-3>log3-0.5=0,
所以0又对任意0=()(1-)<0,所以f(x1)即f(x)在(0,+∞)上单调递增,
所以f(log32)即8.(1)令log2x=t,x∈[,4],
则g(t)=t2+4t+m(t∈[-3,2]).
由于函数f(x)存在大于1的零点,
所以关于t的方程t2+4t+m=0在t∈(0,2]内存在实数根,
由t2+4t+m=0,得m=-t2-4t,t∈(0,2],
所以m∈[-12,0),
所以实数m的取值范围是[-12,0).
(2)函数f(x)有两个互异的零点α,β,
则函数g(t)在[-3,2]内有两个互异的零点t1,t2,其中t1=log2α,t2=log2β,
所以解得3≤m<4,
所以实数m的取值范围是[3,4).
根据根与系数的关系,可知t1+t2=-4,
即log2α+log2β=-4,
所以log2(α·β)=-4,得α·β=2-4=.
(课时1 函数的零点)
一、基础巩固
知识点1 函数的零点
1.函数f(x)=的零点是( )
A.(-1,0),(1,0) B.-1,1
C.(-1,0) D.-1
2.下列图象对应的函数没有零点的是( )
3.[2022河北张家口市第一中学高一月考]函数f(x)=-|lg x|的零点个数为( )
A.0 B.1 C.2 D.3
4.若函数f(x)在定义域(-∞,0)∪(0,+∞)上是偶函数,且在(0,+∞)上是减函数,f(2)=0,则函数f(x)的零点( )
A.只有一个 B.只有两个
C.至少有两个 D.无法判断
5.(多选)[2021山东济宁高一上期中]狄利克雷函数的解析式为D(x)=则( )
A.D(x)≥0
B.D(x)≤1
C.y=D(x)-x3有1个零点
D.y=D(x)+有2个零点
6.[2022上海市大同中学高一上月考]已知x0是函数f(x)=2x+的一个零点,若x1∈(1,x0),x2∈(x0,+∞),则( )
A.f(x1)<0,f(x2)<0
B.f(x1)<0,f(x2)>0
C.f(x1)>0,f(x2)<0
D.f(x1)>0,f(x2)>0
7.[2022广东阳春二中高一上月考]若是函数f(x)=2x2-ax+3的一个零点,则f(x)的另一个零点为 .
知识点2 函数零点存在定理
8.(多选)[2022江苏海安高一上期末]已知函数y=f(x)的图象在区间[0,1]上是一条连续不断的曲线,则下列结论正确的是( )
A.若f(0)f(1)<0,则y=f(x)在(0,1)内至少有一个零点
B.若f(0)f(1)>0,则y= f(x)在(0,1)内没有零点
C.若y=f(x)在(0,1)内没有零点,则必有f(0)f(1)≥0
D.若y=f(x)在(0,1)内有唯一零点,且f(0)f(1)<0,则f(x)在(0,1)上是单调函数
9.[2022江苏淮安高一上期末]已知f(x),g(x)均为[-1,3]上连续不断的曲线,根据下表能判断方程f(x)=g(x)有实数解的区间是( )
x -1 0 1 2 3
f(x) -0.670 3.011 5.432 5.980 7.651
g(x) -0.530 3.451 4.890 5.241 6.892
A.(-1,0) B.(0,1)
C.(1,2) D.(2,3)
10.[2022江苏宿迁高一期末]设方程2x+2x=10的根为β,则β属于( )
A.(0,1) B.(1,2)
C.(2,3) D.(3,4)
11.(多选)已知函数f(x)=ex-x-2,则下列区间中含f(x)的零点的是( )
A.(-2,-1) B.(-1,0)
C.(0,1) D.(1,2)
12.若a
B.(-∞,a)和(a,b)内
C.(b,c)和(c,+∞)内
D.(-∞,a)和(c,+∞)内
13.求证:方程3x=在(0,1)内必有一个实数根.
知识点3 函数的零点的应用
14.已知函数f(x)=2x+x-10的零点x0∈(k,k+1),其中k为整数,则k的值为( )
A.0 B.1 C.2 D.3
15.(多选)[2022江苏省太湖高级中学高二下月考]函数f(x)=2x--a的一个零点在区间(1,2)内,则实数a的可能取值是( )
A.0 B.1 C.2 D.3
16.[2022天津和平区高一上期末]已知函数f(x)=a|x|+m-1(0
C.[0,1) D.[1,2)
17.[2022广东普宁华侨中学高一下月考]已知函数f(x)=若函数g(x)=f(x)-t(t∈R)有3个不同的零点a,b,c,则2a+2b+2c的取值范围是( )
A.[16,32] B.[16,34)
C.(18,32] D.(18,34)
18.[2022上海建平中学高一下月考]设ω>0,若函数y=sin ωx在区间[0,2π]上恰有两个零点,则ω的取值范围为 .
19.已知函数f(x)=-x2+2ex+m-1,g(x)=x+(x>0).
(1)若y=g(x)-m有零点,求实数m的取值范围;
(2)若g(x)-f(x)=0有两个不相等的实根,求实数m的取值范围.
二、能力提升
1.(多选)[2022河北石家庄高一上期末]已知函数f(x)=2x+x,g(x)=log2x+x,h(x)=x3+x的零点分别为a,b,c,则( )
A.-1
3.(多选)[2021广东珠海高一上期末]已知函数f(x)=若f(x1)=f(x2)=f(x3)=f(x4),且x1
C.0
A.(-2,)
B. [-2,]
C.(-∞,-2)∪(,+∞)
D.(-∞,-2]∪[,+∞)
5.[2022北京房山区高三一模]函数f(x)的图象在区间(0,2)上连续不断,写出一个能说明“若f(x)在区间(0,2)上存在零点,则f(0)f(2)<0”为假命题的f(x)= .
6.[2022湖北部分重点高中高一上期末]已知函数f(x)=|2-x-1|,g(x)=且方程f(x)=m有2个不同的解,则实数m的取值范围为 ,方程g(f(x))=m的解的个数为 .
7.[2022江苏镇江高一上期末]已知函数f(x)=3x+a·3-x为偶函数.
(1)求实数a的值;
(2)设函数g(x)=f(x)+x-3-x-3的零点为x0,求证:
(1)若函数f(x)存在大于1的零点,求实数m的取值范围;
(2)设函数f(x)有两个互异的零点α,β,求实数m的取值范围,并求α·β的值.
参考答案
一、基础巩固
1.B 令f(x)=0,则或解得x=-1或x=1.故选B.
2.B 函数图象与x轴无交点即函数没有零点.故选B.
3.C
4.B 因为f(x)在(0,+∞)上是减函数,f(2)=0,所以f(x)在(0,+∞)上有且仅有一个零点2.又f(x)是偶函数,所以f(x)在(-∞,0)上有且仅有一个零点-2.故函数f(x)只有两个零点-2和2.
5.ABC 因为D(x)的值域为{0,1},所以A,B正确.当x是无理数时,由D(x)-x3=0,得0-x3=0,解得x=0,不合题意;当x是有理数时,由D(x)-x3=0,得1-x3=0,解得x=1.则y=D(x)-x3有1个零点,故C正确.令y=D(x)+=0,则D(x)=,当D(x)=1时, x=3+2为无理数,不合题意;当D(x)=0时,x=2为有理数,不合题意.所以y=D(x)+没有零点,故D错误.故选ABC.
6.B
7.1
8.AC
9.B 令h(x)=f(x)-g(x),由表中数据可得,h(-1)<0,h(0)<0,h(1)>0,h(2)>0,h(3)>0.根据零点存在定理,可知h(x)在(0,1)上有零点,故f(x)=g(x)在(0,1)上有实数解.
10.C 设f(x)=2x+2x-10,则f(x)在R上为增函数.又f(2)=-2,f(3)=4,f(2)f(3)<0,所以f(x)在(2,3)上有唯一实根,所以β∈(2,3).
11.AD 因为f(-2)=e-2+2-2=e-2>0,f(-1)=e-1+1-2=e-1-1<0,f(0)=e0-0-2=-1<0,f(1)=e1-1-2=e-3<0,f(2)
=e2-2-2=e2-4>0,所以根据函数零点存在定理,可知区间(-2,-1)和(1,2)中含f(x)的零点.故选AD.
12.A 由于f(a)=(a-b)(a-c)>0,f(b)=(b-c)(b-a)<0,f(c)=(c-a)(c-b)>0,因此f(x)的两个零点分别在区间(a,b)和(b,c)内,故选A.
13.证明:设函数f(x)=3x-=3x+1-.因为y=3x+1与y=-在(0,1)内均为增函数,
所以函数f(x)在(0,1)内是增函数.
又f(0)=30-2=-1<0,f(1)=3->0,即f(0)·f(1)<0,
所以函数f(x)在区间(0,1)内有零点,且只有一个,
即方程3x=在(0,1)内必有一个实数根.
14.C 易知函数f(x)在其定义域内为增函数,故f(x)至多有一个零点.因为f(2)=22+2-10=-4<0,f(3)=23+3-10=1>0,所以f(2)f(3)<0,即函数f(x)在(2,3)内存在一个零点x0.又x0∈(k,k+1),k为整数,所以k=2.
15.BC 因为函数y=2x,y=-在(0,+∞)上单调递增,所以函数f(x)在(0,+∞)上单调递增.由零点存在定理,得f(1)f(2)=-a(3-a)<0,解得0
18.[,1)
19.(1)作出g(x)=x+(x>0),y=m的大致图象,如图1所示.
由图可知若y=g(x)-m有零点,则m≥2e,
所以实数m的取值范围是[2e,+∞).
(2)g(x)-f(x)=0有两个不相等的实根,即g(x)与f(x)的图象有两个交点.
因为f(x)=-x2+2ex+m-1=-(x-e)2+m-1+e2,
所以其图象的对称轴为直线x=e,开口向下,函数f(x)的最大值为m-1+e2.
作出函数f(x)与g(x)的大致图象,如图2所示.
故当m-1+e2>2e,即m>-e2+2e+1时,g(x)与f(x)的图象有两个交点,即g(x)-f(x)=0有两个不相等的实根,
所以实数m的取值范围是(-e2+2e+1,+∞).
二、能力提升
1.AD
2.AC 因为函数f(x)是定义在R上的减函数,且a
5.(x-1)2(答案不唯一)
6.(0,1) 4
7.(1)由f(-x)=f(x),得3x+a·3-x=3-x+a·3x,所以a=1.
(2)由(1)得f(x)=3x+3-x,所以g(x)=3x+3-x+x-3-x-3=3x+x-3.
因为函数g(x)在R上单调递增,且g(log32)=2+log32-3<0,g(log32.5)=2.5+log32.5-3>log3-0.5=0,
所以0
所以f(log32)
则g(t)=t2+4t+m(t∈[-3,2]).
由于函数f(x)存在大于1的零点,
所以关于t的方程t2+4t+m=0在t∈(0,2]内存在实数根,
由t2+4t+m=0,得m=-t2-4t,t∈(0,2],
所以m∈[-12,0),
所以实数m的取值范围是[-12,0).
(2)函数f(x)有两个互异的零点α,β,
则函数g(t)在[-3,2]内有两个互异的零点t1,t2,其中t1=log2α,t2=log2β,
所以解得3≤m<4,
所以实数m的取值范围是[3,4).
根据根与系数的关系,可知t1+t2=-4,
即log2α+log2β=-4,
所以log2(α·β)=-4,得α·β=2-4=.
同课章节目录
- 第1章 集合
- 1.1 集合的概念与表示
- 1.2 子集、全集、补集
- 1.3 交集、并集
- 第2章 常用逻辑用语
- 2.1 命题、定理、定义
- 2.2 充分条件、必要条件、冲要条件
- 2.3 全称量词命题与存在量词命题
- 第3章 不等式
- 3.1 不等式的基本性质
- 3.2 基本不等式
- 3.3 从函数观点看一元二次方程和一元二次不等式
- 第4章 指数与对数
- 4.1 指数
- 4.2 对数
- 第5章 函数概念与性质
- 5.1 函数的概念和图象
- 5.2 函数的表示方法
- 5.3 函数的单调性
- 5.4 函数的奇偶性
- 第6章 幂函数、指数函数和对数函数
- 6.1 幂函数
- 6.2 指数函数
- 6.3 对数函数
- 第7章 三角函数
- 7.1 角与弧度
- 7.2 三角函数概念
- 7.3 三角函数的图象和性质
- 7.4 三角函数应用
- 第8章 函数应用
- 8.1 二分法与求方程近似解
- 8.2 函数与数学模型
