人教版九年级数学上册22.1.2 二次函数y=ax2的图象和性质 一课一练 (word版含答案)
文档属性
| 名称 | 人教版九年级数学上册22.1.2 二次函数y=ax2的图象和性质 一课一练 (word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 96.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-23 08:41:25 | ||
图片预览

文档简介
人教版 九年级数学上册一课一练
22.1.2 二次函数y=ax2的图象和性质
一.选择题
1.已知二次函数y=-x2,下列说法正确的是( )
A.该函数图象经过第一、二象限
B.函数图象有最高点
C.函数图象的对称轴是直线x=-
D.当x<0时,y随x的增大而减小
2.在同一直角坐标系中,抛物线y=4x2,y=x2,y=-x2的共同特点是( )
A. 关于y轴对称,抛物线开口向上
B. 关于y轴对称,y随x的增大而增大
C. 关于y轴对称,y随x的增大而减小
D. 关于y轴对称,抛物线顶点在原点
3.抛物线y=x2的顶点坐标是( )
A.(0,-) B.(0,)
C.(0,0) D.(1,-)
4.下列函数中,当x>0时,y随x增大而减小的是( )
A.y=2x B.y=4x-1
C.y=-3x2 D.y=x2
5. 已知二次函数y=ax2的图象如图,则a满足条件( )
A. a>0 B. a<0
C. a≥0 D. a≤0
6.下列关于函数y=2x2的图象说法:①图象是一条抛物线;②开口向下;③对称轴是y轴;④顶点(0,0),其中正确的有( )
A.1个 B.2个 C.3个 D.4个
7.设点A(-1,y1),B(2,y2),C(3,y3)是抛物线y=x2上的三个点,则y1,y2,y3 的大小关系是( )
A.y1C.y3二.填空题
1.若抛物线y=(n-2)x2开口向下,则n的取值范围为 .
2.二次函数y=-x2的图象开口方向是向 (填“向上”或“向下”)
3.若点(2,y1),(5,y2)是二次函数y=-2x2图象上的两点,则y1与y2的大小关系是 .
4.若点A(3,n)是抛物线y=-x2上的一点,则n=
5.抛物线y=-x2,当x1<x2<0时,y1与y2的大小为 .
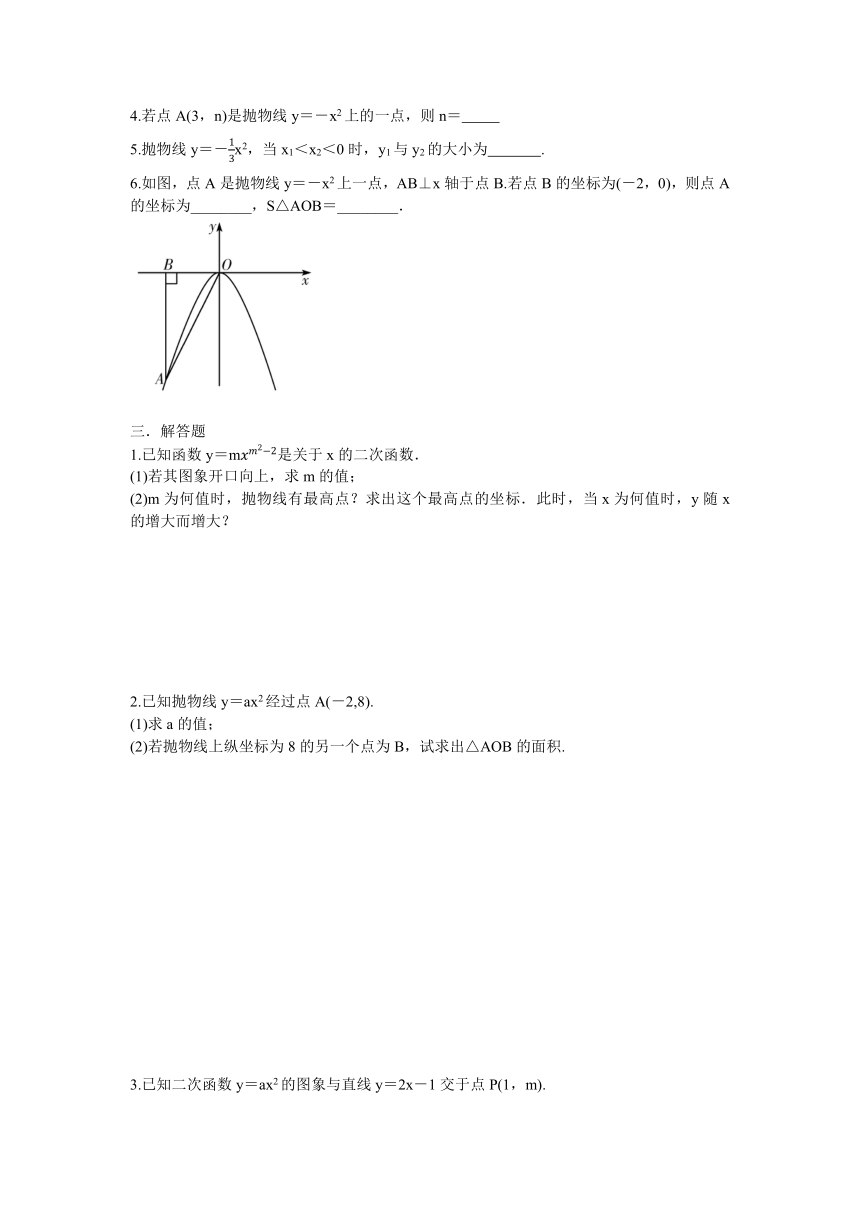
6.如图,点A是抛物线y=-x2上一点,AB⊥x轴于点B.若点B的坐标为(-2,0),则点A的坐标为________,S△AOB=________.
三.解答题
1.已知函数y=m是关于x的二次函数.
(1)若其图象开口向上,求m的值;
(2)m为何值时,抛物线有最高点?求出这个最高点的坐标.此时,当x为何值时,y随x的增大而增大?
2.已知抛物线y=ax2经过点A(-2,8).
(1)求a的值;
(2)若抛物线上纵坐标为8的另一个点为B,试求出△AOB的面积.
3.已知二次函数y=ax2的图象与直线y=2x-1交于点P(1,m).
(1)求a,m的值;
(2)写出二次函数的解析式,并指出x在何范围内,y随x的增大而减小;
(3)指出抛物线y=ax2的顶点坐标和对称轴.
人教版 九年级数学上册一课一练
22.1.2 二次函数y=ax2的图象和性质
参考答案
一.选择题
1.已知二次函数y=-x2,下列说法正确的是( B )
A.该函数图象经过第一、二象限
B.函数图象有最高点
C.函数图象的对称轴是直线x=-
D.当x<0时,y随x的增大而减小
2.在同一直角坐标系中,抛物线y=4x2,y=x2,y=-x2的共同特点是( D )
A. 关于y轴对称,抛物线开口向上
B. 关于y轴对称,y随x的增大而增大
C. 关于y轴对称,y随x的增大而减小
D. 关于y轴对称,抛物线顶点在原点
3.抛物线y=x2的顶点坐标是( C )
A.(0,-) B.(0,)
C.(0,0) D.(1,-)
4.下列函数中,当x>0时,y随x增大而减小的是( C )
A.y=2x B.y=4x-1
C.y=-3x2 D.y=x2
5. 已知二次函数y=ax2的图象如图,则a满足条件( A )
A. a>0 B. a<0
C. a≥0 D. a≤0
6.下列关于函数y=2x2的图象说法:①图象是一条抛物线;②开口向下;③对称轴是y轴;④顶点(0,0),其中正确的有( C )
A.1个 B.2个 C.3个 D.4个
7.设点A(-1,y1),B(2,y2),C(3,y3)是抛物线y=x2上的三个点,则y1,y2,y3 的大小关系是( A )
A.y1C.y3二.填空题
1.若抛物线y=(n-2)x2开口向下,则n的取值范围为 n<2 .
2.二次函数y=-x2的图象开口方向是向 下 (填“向上”或“向下”)
3.若点(2,y1),(5,y2)是二次函数y=-2x2图象上的两点,则y1与y2的大小关系是 y1>y2 .
4.若点A(3,n)是抛物线y=-x2上的一点,则n= -9
5.抛物线y=-x2,当x1<x2<0时,y1与y2的大小为 y16.如图,点A是抛物线y=-x2上一点,AB⊥x轴于点B.若点B的坐标为(-2,0),则点A的坐标为 (-2,-4) ,S△AOB= 4 .
三.解答题
1.已知函数y=m是关于x的二次函数.
(1)若其图象开口向上,求m的值;
(2)m为何值时,抛物线有最高点?求出这个最高点的坐标.此时,当x为何值时,y随x的增大而增大?
解:(1)依题意,得m2-2=2,∴m=±2.
又∵图象开口向上,∴m>0.∴m=2.
(2)当m=-2时,y=-2x2,此时抛物线有最高点,最高点的坐标为(0,0).
此时,当x<0时,y随x的增大而增大.
2.已知抛物线y=ax2经过点A(-2,8).
(1)求a的值;
(2)若抛物线上纵坐标为8的另一个点为B,试求出△AOB的面积.
解:(1)将A(-2,8)代入抛物线y=ax2,得(-2)2a=8. 解得a=2.
(2)由(1)可知,函数的解析式为y=2x2.
当y=8时,2x2=8.
解得x=±2.
则B点坐标为(2,8).
如图
S△AOB=AB·OD=×4×8=16.
3.已知二次函数y=ax2的图象与直线y=2x-1交于点P(1,m).
(1)求a,m的值;
(2)写出二次函数的解析式,并指出x在何范围内,y随x的增大而减小;
(3)指出抛物线y=ax2的顶点坐标和对称轴.
解:(1)由题意,得即
故a,m的值分别为1,1.
(2)二次函数的解析式为y=x2.
当x<0时,y随x的增大而减小.
(3)抛物线y=x2的顶点坐标是(0,0),对称轴是y轴或直线x=0.
22.1.2 二次函数y=ax2的图象和性质
一.选择题
1.已知二次函数y=-x2,下列说法正确的是( )
A.该函数图象经过第一、二象限
B.函数图象有最高点
C.函数图象的对称轴是直线x=-
D.当x<0时,y随x的增大而减小
2.在同一直角坐标系中,抛物线y=4x2,y=x2,y=-x2的共同特点是( )
A. 关于y轴对称,抛物线开口向上
B. 关于y轴对称,y随x的增大而增大
C. 关于y轴对称,y随x的增大而减小
D. 关于y轴对称,抛物线顶点在原点
3.抛物线y=x2的顶点坐标是( )
A.(0,-) B.(0,)
C.(0,0) D.(1,-)
4.下列函数中,当x>0时,y随x增大而减小的是( )
A.y=2x B.y=4x-1
C.y=-3x2 D.y=x2
5. 已知二次函数y=ax2的图象如图,则a满足条件( )
A. a>0 B. a<0
C. a≥0 D. a≤0
6.下列关于函数y=2x2的图象说法:①图象是一条抛物线;②开口向下;③对称轴是y轴;④顶点(0,0),其中正确的有( )
A.1个 B.2个 C.3个 D.4个
7.设点A(-1,y1),B(2,y2),C(3,y3)是抛物线y=x2上的三个点,则y1,y2,y3 的大小关系是( )
A.y1
1.若抛物线y=(n-2)x2开口向下,则n的取值范围为 .
2.二次函数y=-x2的图象开口方向是向 (填“向上”或“向下”)
3.若点(2,y1),(5,y2)是二次函数y=-2x2图象上的两点,则y1与y2的大小关系是 .
4.若点A(3,n)是抛物线y=-x2上的一点,则n=
5.抛物线y=-x2,当x1<x2<0时,y1与y2的大小为 .
6.如图,点A是抛物线y=-x2上一点,AB⊥x轴于点B.若点B的坐标为(-2,0),则点A的坐标为________,S△AOB=________.
三.解答题
1.已知函数y=m是关于x的二次函数.
(1)若其图象开口向上,求m的值;
(2)m为何值时,抛物线有最高点?求出这个最高点的坐标.此时,当x为何值时,y随x的增大而增大?
2.已知抛物线y=ax2经过点A(-2,8).
(1)求a的值;
(2)若抛物线上纵坐标为8的另一个点为B,试求出△AOB的面积.
3.已知二次函数y=ax2的图象与直线y=2x-1交于点P(1,m).
(1)求a,m的值;
(2)写出二次函数的解析式,并指出x在何范围内,y随x的增大而减小;
(3)指出抛物线y=ax2的顶点坐标和对称轴.
人教版 九年级数学上册一课一练
22.1.2 二次函数y=ax2的图象和性质
参考答案
一.选择题
1.已知二次函数y=-x2,下列说法正确的是( B )
A.该函数图象经过第一、二象限
B.函数图象有最高点
C.函数图象的对称轴是直线x=-
D.当x<0时,y随x的增大而减小
2.在同一直角坐标系中,抛物线y=4x2,y=x2,y=-x2的共同特点是( D )
A. 关于y轴对称,抛物线开口向上
B. 关于y轴对称,y随x的增大而增大
C. 关于y轴对称,y随x的增大而减小
D. 关于y轴对称,抛物线顶点在原点
3.抛物线y=x2的顶点坐标是( C )
A.(0,-) B.(0,)
C.(0,0) D.(1,-)
4.下列函数中,当x>0时,y随x增大而减小的是( C )
A.y=2x B.y=4x-1
C.y=-3x2 D.y=x2
5. 已知二次函数y=ax2的图象如图,则a满足条件( A )
A. a>0 B. a<0
C. a≥0 D. a≤0
6.下列关于函数y=2x2的图象说法:①图象是一条抛物线;②开口向下;③对称轴是y轴;④顶点(0,0),其中正确的有( C )
A.1个 B.2个 C.3个 D.4个
7.设点A(-1,y1),B(2,y2),C(3,y3)是抛物线y=x2上的三个点,则y1,y2,y3 的大小关系是( A )
A.y1
1.若抛物线y=(n-2)x2开口向下,则n的取值范围为 n<2 .
2.二次函数y=-x2的图象开口方向是向 下 (填“向上”或“向下”)
3.若点(2,y1),(5,y2)是二次函数y=-2x2图象上的两点,则y1与y2的大小关系是 y1>y2 .
4.若点A(3,n)是抛物线y=-x2上的一点,则n= -9
5.抛物线y=-x2,当x1<x2<0时,y1与y2的大小为 y1
三.解答题
1.已知函数y=m是关于x的二次函数.
(1)若其图象开口向上,求m的值;
(2)m为何值时,抛物线有最高点?求出这个最高点的坐标.此时,当x为何值时,y随x的增大而增大?
解:(1)依题意,得m2-2=2,∴m=±2.
又∵图象开口向上,∴m>0.∴m=2.
(2)当m=-2时,y=-2x2,此时抛物线有最高点,最高点的坐标为(0,0).
此时,当x<0时,y随x的增大而增大.
2.已知抛物线y=ax2经过点A(-2,8).
(1)求a的值;
(2)若抛物线上纵坐标为8的另一个点为B,试求出△AOB的面积.
解:(1)将A(-2,8)代入抛物线y=ax2,得(-2)2a=8. 解得a=2.
(2)由(1)可知,函数的解析式为y=2x2.
当y=8时,2x2=8.
解得x=±2.
则B点坐标为(2,8).
如图
S△AOB=AB·OD=×4×8=16.
3.已知二次函数y=ax2的图象与直线y=2x-1交于点P(1,m).
(1)求a,m的值;
(2)写出二次函数的解析式,并指出x在何范围内,y随x的增大而减小;
(3)指出抛物线y=ax2的顶点坐标和对称轴.
解:(1)由题意,得即
故a,m的值分别为1,1.
(2)二次函数的解析式为y=x2.
当x<0时,y随x的增大而减小.
(3)抛物线y=x2的顶点坐标是(0,0),对称轴是y轴或直线x=0.
同课章节目录
