湖南省衡阳市第六中学2022-2023学年高一上学期8月入学考试数学试题(Word版含解析)
文档属性
| 名称 | 湖南省衡阳市第六中学2022-2023学年高一上学期8月入学考试数学试题(Word版含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 749.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-22 10:23:47 | ||
图片预览



文档简介
衡阳市第六中学2022-2023学年高一上学期8月入学考试
数学
班级:__________.姓名:__________.准考证号:__________.
(全卷满分:150分,考试用时:120分钟)
注意事项:
1.答题前,先将自己的姓名 准考证号写在试题卷和答题卡上,并将准考证号条形码粘贴在答题卡上的指定位置.
2.选择题的作答:每小题选出答案后,用2B铅笔把答题卡上相应题目的答案标号涂黑.写在试题卷 草稿纸和答题卡上的非答题区域均无效.
3.非选择题的作答:用签字笔直接答在答题卡上对应的答题区域内,写在试题卷 草稿纸和答题卡上的非答题区域均无效.
4.考试结束后,将本试题卷和答题卷一并上交.
第I卷(选择题共60分)
一、选择题:本大题共15小题,每小题4分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.下列各数为无理数的是( )
A. B. C. D.
2.将一个五角星逆时针旋转n°后与原图形完全重合,则n的最小值为( )
A.54 B.60 C.72 D.75
3.我国古代数学名著《九章算术》中有这样一段记载:“今有共买豕,人出一百,盈一百:人出九十,适足.问人数 豕价各几何?”大意是若干个人合买一头猪,若每人出100钱,则会剩下100钱;若每人出90钱,则不多也不少.问人数 猪价各多少?设人数 猪价分别为x y,则可列方程组为( )
A. B.
C. D.
4.若,其中为整数,则的值为( )
A.3或9 B. C. D.或
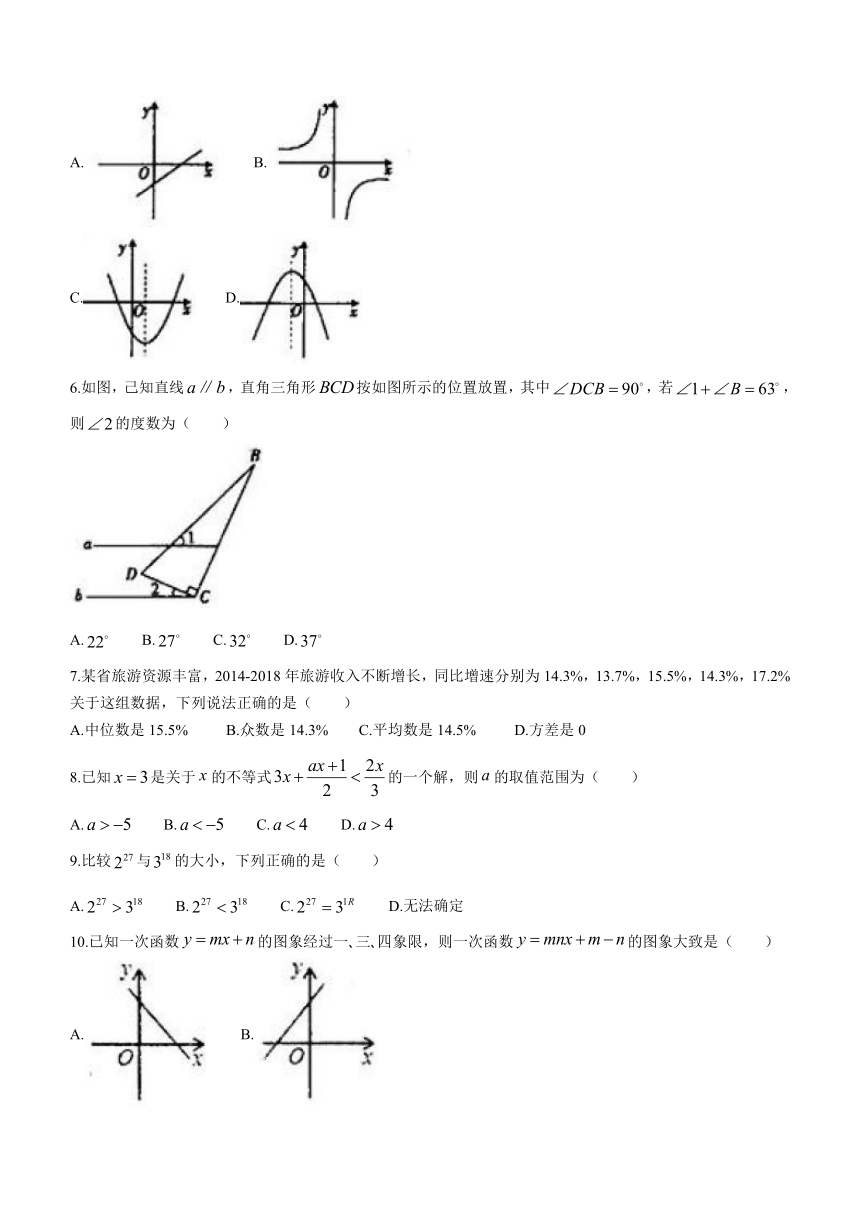
5.下列四个函数图象中,当时,函数值随自变量的增大而减小的是( )
A. B.
C. D.
6.如图,己知直线,直角三角形按如图所示的位置放置,其中,若,则的度数为( )
A. B. C. D.
7.某省旅游资源丰富,2014-2018年旅游收入不断增长,同比增速分别为14.3%,13.7%,15.5%,14.3%,17.2%关于这组数据,下列说法正确的是( )
A.中位数是15.5% B.众数是14.3% C.平均数是14.5% D.方差是0
8.已知是关于的不等式的一个解,则的取值范围为( )
A. B. C. D.
9.比较与的大小,下列正确的是( )
A. B. C. D.无法确定
10.已知一次函数的图象经过一 三 四象限,则一次函数的图象大致是( )
A. B.
C. D.
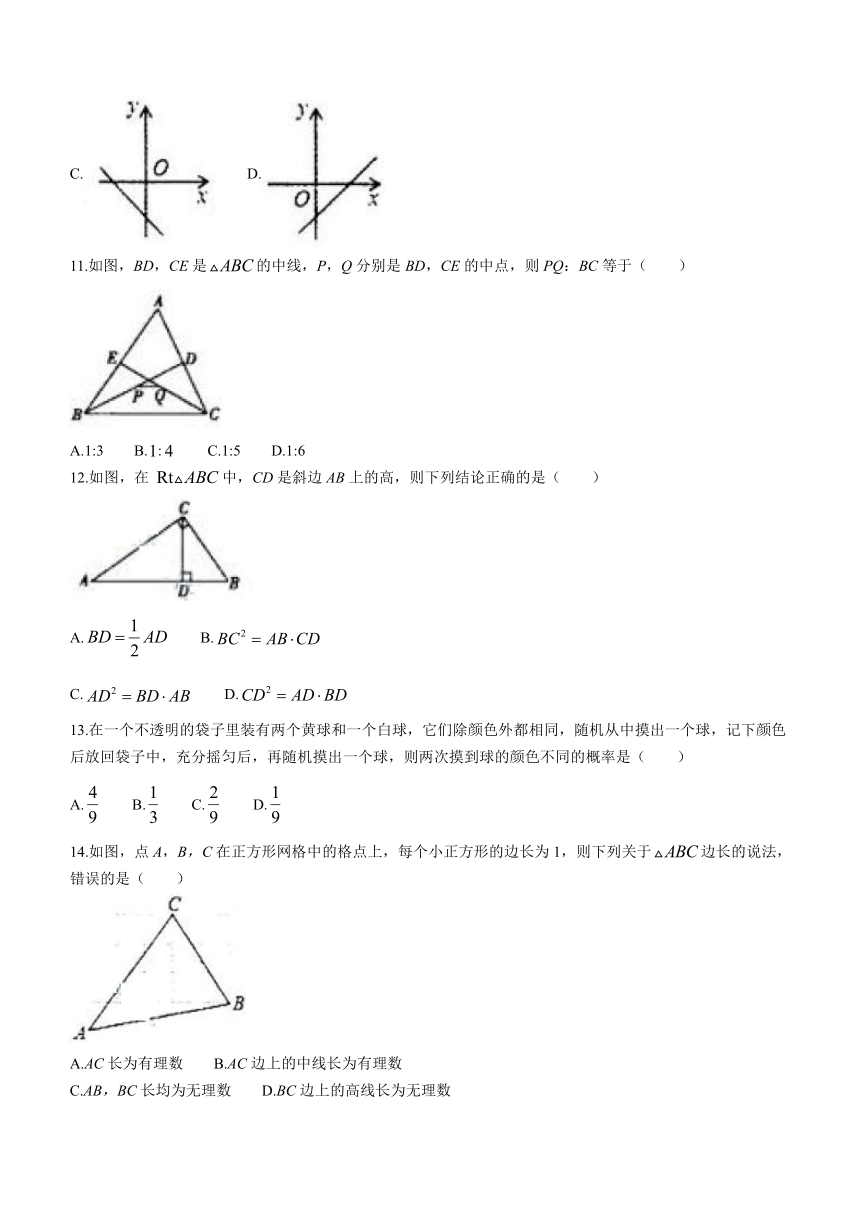
11.如图,BD,CE是的中线,P,Q分别是BD,CE的中点,则PQ:BC等于( )
A.1:3 B.: C.1:5 D.1:6
12.如图,在中,CD是斜边AB上的高,则下列结论正确的是( )
A. B.
C. D.
13.在一个不透明的袋子里装有两个黄球和一个白球,它们除颜色外都相同,随机从中摸出一个球,记下颜色后放回袋子中,充分摇匀后,再随机摸出一个球,则两次摸到球的颜色不同的概率是( )
A. B. C. D.
14.如图,点A,B,C在正方形网格中的格点上,每个小正方形的边长为1,则下列关于边长的说法,错误的是( )
A.AC长为有理数 B.AC边上的中线长为有理数
C.AB,BC长均为无理数 D.BC边上的高线长为无理数
15.已知二次函数,一次函数,点为二次函数图象上的动点,点为一次函数图象上的动点,若存在四个的值,使得,则的取值范围是( )
A. B.
C.或 D.
第II卷(非选择题共90分)
二 填空题:本大题共4小题,每小题5分,共20分.
16.计算__________.
17.如图,已知和的平分线相交于点 若 则__________.
18.如图,在Rt中,,以点为圆心,为半径画弧交于点,作,垂足为点,则__________.
19.如图,是反比例函数的图象在第一象限中的一点,为原点,点在轴上,点在轴上,四边形为直角梯形,,若梯形的面积为6,则反比例函数的解析式为__________.
三 解答题:本大题共6小题,共70分,其中第20题10分,第22至25题每小题12分,解答应写出文字说明 证明过程或演算步骤.
20.已知关于的方程.
(1)若方程有两个不相等的实数根,求的取值范围;
(2)若,设为方程的两根,求的值.
21.某商场为调查商场内某品牌家电的受欢迎程度,对商场内的顾客进行了问卷调查,并对问卷调查的结果分为“非常喜欢” “比较喜欢” “感觉一般” “不太喜欢”四个等级,分别记作A B C D.根据调查结果绘制出如图所示的扇形统计图和条形统计图,请结合图中所给信息解答下列问题:
(1)将条形统计图补充完整,并标明数据;
(2)若选择“不太喜欢”的人中有一位女士,三位男士,从这四个人中挑选两个人体验使用最新型的家电产品,请用画树状图或列表法,求该女士被选中的概率;
(3)已知选择A B等级的人数需要达到,商场才评定该品牌家电为“优质品牌”.若有四人体验了该品牌在商场展示的最新型的家电产品后,又提交了4份等级为的调查问卷,与之前的调查结果合并在一起,问该品牌家电在此次调查中是否获得商场“优质品牌”评定?
22.(12分)如图,在Rt中,,点是上一点,
(1)若为的角平分线,求的长:
(2)若,求的值.
23.(12分)如图,在中,以斜边为直径作,延长至点,恰好使得,过点作于点,延长交于点.
(1)求证:CE是的切线.
(2)若,求的长.
24.(12分)正方形的边长为1,点是对角线上一动点.
(1)如图1,过点作,垂足分别为点,求证:.
(2)如图2,点是边上的点,连接的值是丕随点的位置改变而改变?若不变,求出它的值;若改变,请说明理由.
(3)如图3,求的最小值.
25.(12分)在平面直角坐标标系中,抛物线经过点和两点.
(1)求的值及满足的关系式.
(2)已知点是拋物线上的两个点,求证:.
(3)若拋物线与直线相交于点,求a的值.
衡阳市第六中学2022-2023学年高一上学期8月入学考试
(数学)
参考答案
一 选择题:本大题共15小题,每小题4分,共60分.
1.A
2.D
3.C
4.D
5.C【解析】观察图象知,在x<0时,只有C选项中的函数值y随自变量x的增大而减小,故选C.
6.B【解析】由题意可知,∠1+∠B+∠2+∠DCB=180°,又∠1+∠B=63°,∠DCB=90°,所以∠2=27°.
7.B【解析】将这组数据按从小到大的顺序排列为13.7%,14.3%,14.3%,15.5%,17.2%,中位数是14.3%,故A选项错误;
8.B【解析】将“x=3”代入不等式可得,解得.
9.B【解析】因为,,所以,故选B.
10.A【解析】因为一次函数y=mx+n的图象经过一 三 四象限,所以m>0,n<0,所以mn<0,m-n>0,所以一次函数y=mnx+m﹣n的图象经过一 二 四象限.观察各选项中的图象可知,选A.
11.B
12.D【解析】由△ADC∽△CDB得,则.故选D.
13.A【解析】画树状图如图所示,
由树状图可知,共有9种等可能的结果,其中两次摸到球的颜色不同的结果有4种,
故两次摸到球的颜色不同的概率为.故选A.
14.B【解析】由勾股定理,得AC==5,是有理数,故A正确;BC==,是无理数,AB==,是无理数,故C正确;S△ABC=20-×5×1-×4×3-×3×2=,BC边上的高为2S△ABC÷BC=,故D正确.故选B.
15.C【解析】由题意得,.
当时,即,恒成立.
当时,即,由,解得.
综上,选C.
二 填空题:本大题共4小题,每小题5分,共20分.
16.3
17.120°【解析】因为∠F=∠ABF+∠CDF,∠ABF=∠FBE,∠CDF=∠FDE,
所以∠F=∠FBE+∠FDE.
又在四边形中,∠BFD+∠FDE+∠E+∠EBF=360°,∠E=∠F,
所以∠E=120°.
18.
19.y=
三 解答题:本大题共6小题,共70分,其中第20题10分,第22至25题每小题12分,解答应写出文字说明 证明过程或演算步骤.
20.解:(1)∵方程有两个不相等的实数根,
∴,
解得k<4.
(2)当k=1时,
∵,为方程的两根,
∴,,,,
∴=1.
21.解:(1)补全图形如下所示.
(2)列表如下:
女 男1 男2 男3
女 (女,男1) (女,男2) (女,男3)
男1 (女,男1) (男1,男2) (男1,男3)
男2 (女,男2) (男1,男2) (男2,男3)
男3 (女,男3) (男1,男3) (男2,男3)
由表可知,共有12种等可能的结果,其中挑选的人中包含了女士的有6种结果,
∴.
(3)由于<80%,
所以该品牌家电在此次调查中不能获得商场“优质品牌”评定.
22.解:(1)过点D作DH⊥AB于点H,
∵∠C=90°,AC=BC,
∴∠A=45°.
∵DH⊥AB,
∴AH=DH.
设AH=x,则DH=x,
∴.
∵BD为∠ABC的角平分线,
∴CD=DH=x,
∴AD+CD=+x=4,
解得.
∴.
(2)同(1)过点D作DH⊥AB于点H,
由(1)可知AH=DH,
设AH=a,则DH=a,
∵,
∴BH=5a,
∴AB=AH+BH=6a,
由勾股定理可知,AB=,
∴a=,即AH=DH=,
∴AD==.
∴CD=ACAD=.
∵,
∴BD=,
∴sin∠DBC=.
23.【解析】(1)∵OB=OC,∴∠ABC=∠OCB.
∵AB=AD,
∴∠ABC=∠ADB,
∴∠OCB=∠ADB,
∴OC∥AD.
∵CE⊥AD,
∴∠AEC=∠OCE=90°,∴OC⊥CE,
∴CE是☉O的切线.
(2)如图,过点O作OH⊥AF于点H,则∠OCE=∠CEH=∠OHE=90°,
∴四边形OCEH是矩形,
∴OC=EH,OH=CE.
设AH=x,
∵CE+AE=4,OC=5,
∴AE=5x,OH=CE=4(5x)=x1.
在Rt△AOH中,由勾股定理知AH2+OH2=OA2,即x2+(x1)2=25,
解得x1=4,x2=3(不合题意,舍去).
∴AH=4.
∵OH⊥AF,
∴AH=FH=AF,
∴AF=2AH=2×4=8.
24.(1)证明:∵四边形ABCD是正方形,∴∠ABC=90°.
∵BD是正方形ABCD的对角线,∴∠ABD=∠CBD=45°.
∵MH⊥AB,MG⊥BC,
∴∠BHM=∠BGM=90°,
在△BHM和△BGM中,BM=MB,∠ABD=∠CBD,∠BHM=∠BGM,
∴△BHM≌△BGM,
∴HM=GM.
(2)的值不会变化.
如图,连接AM,
图
∵四边形ABCD是正方形,BD是正方形的对角线,
∴∠ABM=∠CBM=45°,AB=BC.
∵BM=MB,
∴△ABM≌△CBM,
∴AM=CM,∠BCM=∠BAM,
∵在四边形BCME中,∠ABC=∠EMC=90°,
∴∠BCM+∠BEM=360°∠ABC∠EMC=180°,
∵∠AEM+∠BEM=180°,
∴∠BCM=∠AEM,
∴∠AEM=∠BAM,
∴EM=AM,
∴EM=CM,
∵,
∴,
∴.
(3)如图,将BM绕点B逆时针旋转60°,得到线段BM′,连接MM′.
图
易证△BM′M是等边三角形.
将BC绕点B逆时针旋转150°,得到线段BC′,连接CC′ C′M′,则∠C′BM′=45°.
易证△BCM≌△BC′M′,∴C′M′=CM.
当点C′ M′ M C在同一直线上时,BM+2CM的值最小,
此时BM+2CM=M′M+CM+C′M′=C′C.
过点C′作C′H⊥BC,交CB的延长线于点H.
在Rt△C′BH中,BC′=2,∠C′BH=30°,
∴C′H=1,BH=,
∴C′C===2,
故BM+2CM的最小值为2.
25.解:(1)∵抛物线经过点A(0,4)和B(2,0),
∴
∴2a+b=2.
(2)由(1)可得抛物线表达式为,
将点C(a,b),D(a+2,c)的坐标代入抛物线的表达式,
得b=,c=,
∴.
(3)∵点M N是直线y=2x3与抛物线的交点,
∴p和2p是方程的两个根,
整理得,
∴p+(2p)=,
∴a=1.
数学
班级:__________.姓名:__________.准考证号:__________.
(全卷满分:150分,考试用时:120分钟)
注意事项:
1.答题前,先将自己的姓名 准考证号写在试题卷和答题卡上,并将准考证号条形码粘贴在答题卡上的指定位置.
2.选择题的作答:每小题选出答案后,用2B铅笔把答题卡上相应题目的答案标号涂黑.写在试题卷 草稿纸和答题卡上的非答题区域均无效.
3.非选择题的作答:用签字笔直接答在答题卡上对应的答题区域内,写在试题卷 草稿纸和答题卡上的非答题区域均无效.
4.考试结束后,将本试题卷和答题卷一并上交.
第I卷(选择题共60分)
一、选择题:本大题共15小题,每小题4分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.下列各数为无理数的是( )
A. B. C. D.
2.将一个五角星逆时针旋转n°后与原图形完全重合,则n的最小值为( )
A.54 B.60 C.72 D.75
3.我国古代数学名著《九章算术》中有这样一段记载:“今有共买豕,人出一百,盈一百:人出九十,适足.问人数 豕价各几何?”大意是若干个人合买一头猪,若每人出100钱,则会剩下100钱;若每人出90钱,则不多也不少.问人数 猪价各多少?设人数 猪价分别为x y,则可列方程组为( )
A. B.
C. D.
4.若,其中为整数,则的值为( )
A.3或9 B. C. D.或
5.下列四个函数图象中,当时,函数值随自变量的增大而减小的是( )
A. B.
C. D.
6.如图,己知直线,直角三角形按如图所示的位置放置,其中,若,则的度数为( )
A. B. C. D.
7.某省旅游资源丰富,2014-2018年旅游收入不断增长,同比增速分别为14.3%,13.7%,15.5%,14.3%,17.2%关于这组数据,下列说法正确的是( )
A.中位数是15.5% B.众数是14.3% C.平均数是14.5% D.方差是0
8.已知是关于的不等式的一个解,则的取值范围为( )
A. B. C. D.
9.比较与的大小,下列正确的是( )
A. B. C. D.无法确定
10.已知一次函数的图象经过一 三 四象限,则一次函数的图象大致是( )
A. B.
C. D.
11.如图,BD,CE是的中线,P,Q分别是BD,CE的中点,则PQ:BC等于( )
A.1:3 B.: C.1:5 D.1:6
12.如图,在中,CD是斜边AB上的高,则下列结论正确的是( )
A. B.
C. D.
13.在一个不透明的袋子里装有两个黄球和一个白球,它们除颜色外都相同,随机从中摸出一个球,记下颜色后放回袋子中,充分摇匀后,再随机摸出一个球,则两次摸到球的颜色不同的概率是( )
A. B. C. D.
14.如图,点A,B,C在正方形网格中的格点上,每个小正方形的边长为1,则下列关于边长的说法,错误的是( )
A.AC长为有理数 B.AC边上的中线长为有理数
C.AB,BC长均为无理数 D.BC边上的高线长为无理数
15.已知二次函数,一次函数,点为二次函数图象上的动点,点为一次函数图象上的动点,若存在四个的值,使得,则的取值范围是( )
A. B.
C.或 D.
第II卷(非选择题共90分)
二 填空题:本大题共4小题,每小题5分,共20分.
16.计算__________.
17.如图,已知和的平分线相交于点 若 则__________.
18.如图,在Rt中,,以点为圆心,为半径画弧交于点,作,垂足为点,则__________.
19.如图,是反比例函数的图象在第一象限中的一点,为原点,点在轴上,点在轴上,四边形为直角梯形,,若梯形的面积为6,则反比例函数的解析式为__________.
三 解答题:本大题共6小题,共70分,其中第20题10分,第22至25题每小题12分,解答应写出文字说明 证明过程或演算步骤.
20.已知关于的方程.
(1)若方程有两个不相等的实数根,求的取值范围;
(2)若,设为方程的两根,求的值.
21.某商场为调查商场内某品牌家电的受欢迎程度,对商场内的顾客进行了问卷调查,并对问卷调查的结果分为“非常喜欢” “比较喜欢” “感觉一般” “不太喜欢”四个等级,分别记作A B C D.根据调查结果绘制出如图所示的扇形统计图和条形统计图,请结合图中所给信息解答下列问题:
(1)将条形统计图补充完整,并标明数据;
(2)若选择“不太喜欢”的人中有一位女士,三位男士,从这四个人中挑选两个人体验使用最新型的家电产品,请用画树状图或列表法,求该女士被选中的概率;
(3)已知选择A B等级的人数需要达到,商场才评定该品牌家电为“优质品牌”.若有四人体验了该品牌在商场展示的最新型的家电产品后,又提交了4份等级为的调查问卷,与之前的调查结果合并在一起,问该品牌家电在此次调查中是否获得商场“优质品牌”评定?
22.(12分)如图,在Rt中,,点是上一点,
(1)若为的角平分线,求的长:
(2)若,求的值.
23.(12分)如图,在中,以斜边为直径作,延长至点,恰好使得,过点作于点,延长交于点.
(1)求证:CE是的切线.
(2)若,求的长.
24.(12分)正方形的边长为1,点是对角线上一动点.
(1)如图1,过点作,垂足分别为点,求证:.
(2)如图2,点是边上的点,连接的值是丕随点的位置改变而改变?若不变,求出它的值;若改变,请说明理由.
(3)如图3,求的最小值.
25.(12分)在平面直角坐标标系中,抛物线经过点和两点.
(1)求的值及满足的关系式.
(2)已知点是拋物线上的两个点,求证:.
(3)若拋物线与直线相交于点,求a的值.
衡阳市第六中学2022-2023学年高一上学期8月入学考试
(数学)
参考答案
一 选择题:本大题共15小题,每小题4分,共60分.
1.A
2.D
3.C
4.D
5.C【解析】观察图象知,在x<0时,只有C选项中的函数值y随自变量x的增大而减小,故选C.
6.B【解析】由题意可知,∠1+∠B+∠2+∠DCB=180°,又∠1+∠B=63°,∠DCB=90°,所以∠2=27°.
7.B【解析】将这组数据按从小到大的顺序排列为13.7%,14.3%,14.3%,15.5%,17.2%,中位数是14.3%,故A选项错误;
8.B【解析】将“x=3”代入不等式可得,解得.
9.B【解析】因为,,所以,故选B.
10.A【解析】因为一次函数y=mx+n的图象经过一 三 四象限,所以m>0,n<0,所以mn<0,m-n>0,所以一次函数y=mnx+m﹣n的图象经过一 二 四象限.观察各选项中的图象可知,选A.
11.B
12.D【解析】由△ADC∽△CDB得,则.故选D.
13.A【解析】画树状图如图所示,
由树状图可知,共有9种等可能的结果,其中两次摸到球的颜色不同的结果有4种,
故两次摸到球的颜色不同的概率为.故选A.
14.B【解析】由勾股定理,得AC==5,是有理数,故A正确;BC==,是无理数,AB==,是无理数,故C正确;S△ABC=20-×5×1-×4×3-×3×2=,BC边上的高为2S△ABC÷BC=,故D正确.故选B.
15.C【解析】由题意得,.
当时,即,恒成立.
当时,即,由,解得.
综上,选C.
二 填空题:本大题共4小题,每小题5分,共20分.
16.3
17.120°【解析】因为∠F=∠ABF+∠CDF,∠ABF=∠FBE,∠CDF=∠FDE,
所以∠F=∠FBE+∠FDE.
又在四边形中,∠BFD+∠FDE+∠E+∠EBF=360°,∠E=∠F,
所以∠E=120°.
18.
19.y=
三 解答题:本大题共6小题,共70分,其中第20题10分,第22至25题每小题12分,解答应写出文字说明 证明过程或演算步骤.
20.解:(1)∵方程有两个不相等的实数根,
∴,
解得k<4.
(2)当k=1时,
∵,为方程的两根,
∴,,,,
∴=1.
21.解:(1)补全图形如下所示.
(2)列表如下:
女 男1 男2 男3
女 (女,男1) (女,男2) (女,男3)
男1 (女,男1) (男1,男2) (男1,男3)
男2 (女,男2) (男1,男2) (男2,男3)
男3 (女,男3) (男1,男3) (男2,男3)
由表可知,共有12种等可能的结果,其中挑选的人中包含了女士的有6种结果,
∴.
(3)由于<80%,
所以该品牌家电在此次调查中不能获得商场“优质品牌”评定.
22.解:(1)过点D作DH⊥AB于点H,
∵∠C=90°,AC=BC,
∴∠A=45°.
∵DH⊥AB,
∴AH=DH.
设AH=x,则DH=x,
∴.
∵BD为∠ABC的角平分线,
∴CD=DH=x,
∴AD+CD=+x=4,
解得.
∴.
(2)同(1)过点D作DH⊥AB于点H,
由(1)可知AH=DH,
设AH=a,则DH=a,
∵,
∴BH=5a,
∴AB=AH+BH=6a,
由勾股定理可知,AB=,
∴a=,即AH=DH=,
∴AD==.
∴CD=ACAD=.
∵,
∴BD=,
∴sin∠DBC=.
23.【解析】(1)∵OB=OC,∴∠ABC=∠OCB.
∵AB=AD,
∴∠ABC=∠ADB,
∴∠OCB=∠ADB,
∴OC∥AD.
∵CE⊥AD,
∴∠AEC=∠OCE=90°,∴OC⊥CE,
∴CE是☉O的切线.
(2)如图,过点O作OH⊥AF于点H,则∠OCE=∠CEH=∠OHE=90°,
∴四边形OCEH是矩形,
∴OC=EH,OH=CE.
设AH=x,
∵CE+AE=4,OC=5,
∴AE=5x,OH=CE=4(5x)=x1.
在Rt△AOH中,由勾股定理知AH2+OH2=OA2,即x2+(x1)2=25,
解得x1=4,x2=3(不合题意,舍去).
∴AH=4.
∵OH⊥AF,
∴AH=FH=AF,
∴AF=2AH=2×4=8.
24.(1)证明:∵四边形ABCD是正方形,∴∠ABC=90°.
∵BD是正方形ABCD的对角线,∴∠ABD=∠CBD=45°.
∵MH⊥AB,MG⊥BC,
∴∠BHM=∠BGM=90°,
在△BHM和△BGM中,BM=MB,∠ABD=∠CBD,∠BHM=∠BGM,
∴△BHM≌△BGM,
∴HM=GM.
(2)的值不会变化.
如图,连接AM,
图
∵四边形ABCD是正方形,BD是正方形的对角线,
∴∠ABM=∠CBM=45°,AB=BC.
∵BM=MB,
∴△ABM≌△CBM,
∴AM=CM,∠BCM=∠BAM,
∵在四边形BCME中,∠ABC=∠EMC=90°,
∴∠BCM+∠BEM=360°∠ABC∠EMC=180°,
∵∠AEM+∠BEM=180°,
∴∠BCM=∠AEM,
∴∠AEM=∠BAM,
∴EM=AM,
∴EM=CM,
∵,
∴,
∴.
(3)如图,将BM绕点B逆时针旋转60°,得到线段BM′,连接MM′.
图
易证△BM′M是等边三角形.
将BC绕点B逆时针旋转150°,得到线段BC′,连接CC′ C′M′,则∠C′BM′=45°.
易证△BCM≌△BC′M′,∴C′M′=CM.
当点C′ M′ M C在同一直线上时,BM+2CM的值最小,
此时BM+2CM=M′M+CM+C′M′=C′C.
过点C′作C′H⊥BC,交CB的延长线于点H.
在Rt△C′BH中,BC′=2,∠C′BH=30°,
∴C′H=1,BH=,
∴C′C===2,
故BM+2CM的最小值为2.
25.解:(1)∵抛物线经过点A(0,4)和B(2,0),
∴
∴2a+b=2.
(2)由(1)可得抛物线表达式为,
将点C(a,b),D(a+2,c)的坐标代入抛物线的表达式,
得b=,c=,
∴.
(3)∵点M N是直线y=2x3与抛物线的交点,
∴p和2p是方程的两个根,
整理得,
∴p+(2p)=,
∴a=1.
同课章节目录
