人教A版2019必修二第九章 概率 单元测试卷(Word版含解析)
文档属性
| 名称 | 人教A版2019必修二第九章 概率 单元测试卷(Word版含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 385.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
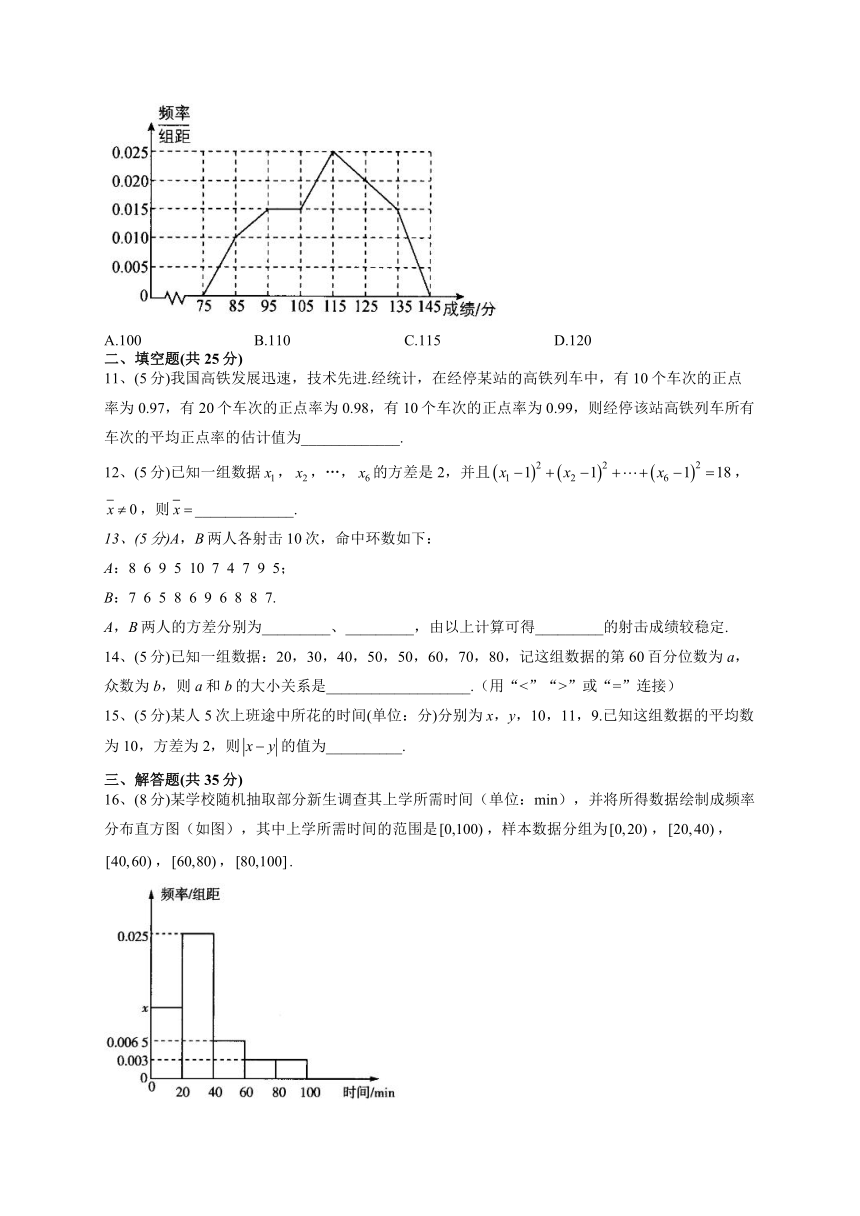
| 更新时间 | 2022-08-22 00:00:00 | ||
图片预览



文档简介
第九章 概率 单元测试卷
学校:___________姓名:___________班级:___________考号:___________
一、选择题(共40分)
1、(4分)某校为了对初三学生的体重进行摸底调查,随机抽取了50名学生的体重(kg),将所得数据整理后,画出了频率分布直方图.如图所示,体重在内适合跑步训练,体重在内适合跳远训练,体重在内适合投掷相关方面训练,估计该校初三学生适合参加跑步、跳远、投掷三项训练的集训人数之比为( )
A.4:3:1 B.5:3:1 C.5:3:2 D.3:2:1
2、(4分)设一组样本数据,,…,的方差为0.01,则数据,,…,的方差为( )
A.0.01 B.0.1 C.1 D.10
3、(4分)演讲比赛共有9位评委分别给出某选手的原始评分,评定该选手的成绩时,从9个原始评分中去掉1个最高分、1个最低分,得到7个有效评分.7个有效评分与9个原始评分相比,不变的数字特征是( )
A.中位数 B.平均数 C.方差 D.极差
4、(4分)某班全体学生参加一次测试,将所得分数依次分组:,,,,绘制出如图所示的成绩频率分布直方图.若低于60分的人数是18,则该班的学生人数是( )
A.50 B.54 C.60 D.64
5、(4分)某中学初中部共有120名教师,高中部共有150名教师,其性别比例如图所示,则该校女教师的人数为( )
A.128 B.144 C.174 D.167
6、(4分)某创业公司共有36名职工,为了了解该公司职工的年龄构成情况,随机采访了9名职工的年龄数据分别为36,36,37,37,44,40,43,44,43.若用样本估计总体,则年龄在内的人数占公司总人数的百分比是(精确到1%)( )
A.56% B.14% C.25% D.67%
7、(4分)期中考试后,班长算出了全班40个同学数学成绩的平均数为M.如果把M当成一个同学的分数,与原来的40个分数一起,算出这41个分数的平均数为N,那么为( )
A. B.1 C. D.2
8、(4分)在样本的频率分布直方图中,共有9个小长方形.若中间一个长方形的面积等于其他8个小长方形面积之和的,且样本量为200,则中间一组的频数为( )
A.0.2 B.0.25 C.40 D.50
9、(4分)某学校的教师配置比例如图所示,为了调查各类教师的薪资状况,现采用分层随机抽样的方法抽取部分教师进行调查.在抽取的样本中,青年教师30人,则该样本中的老年教师人数为( )
A.10 B.12 C.18 D.20
10、(4分)某同学将全班某次数学考试成绩整理成频率分布直方图后,并将每个小矩形上方线段的中点连接起来得到频率折线图(如图所示),据此估计此次考试成绩的众数是( )
A.100 B.110 C.115 D.120
二、填空题(共25分)
11、(5分)我国高铁发展迅速,技术先进.经统计,在经停某站的高铁列车中,有10个车次的正点率为0.97,有20个车次的正点率为0.98,有10个车次的正点率为0.99,则经停该站高铁列车所有车次的平均正点率的估计值为_____________.
12、(5分)已知一组数据,,…,的方差是2,并且,,则_____________.
13、(5分)A,B两人各射击10次,命中环数如下:
A:8 6 9 5 10 7 4 7 9 5;
B:7 6 5 8 6 9 6 8 8 7.
A,B两人的方差分别为_________、_________,由以上计算可得_________的射击成绩较稳定.
14、(5分)已知一组数据:20,30,40,50,50,60,70,80,记这组数据的第60百分位数为a,众数为b,则a和b的大小关系是___________________.(用“<”“>”或“=”连接)
15、(5分)某人5次上班途中所花的时间(单位:分)分别为x,y,10,11,9.已知这组数据的平均数为10,方差为2,则的值为__________.
三、解答题(共35分)
16、(8分)某学校随机抽取部分新生调查其上学所需时间(单位:min),并将所得数据绘制成频率分布直方图(如图),其中上学所需时间的范围是,样本数据分组为,,,,.
(1)求频率分布直方图中x的值;
(2)假设上学所需时间不少于1 h的学生可申请在学校住宿,若该学校有600名新生,请估计新生中有多少名学生可以申请住宿;
(3)由频率分布直方图估计该校新生上学所需时间的平均值.
17、(9分)某校从参加高一年级期末考试的学生中抽出60名学生,将其成绩(均为整数)分成六段后画出如图部分频率分布直方图.观察图形的信息,回答下列问题:
(1)求第四小组的频率,并补全这个频率分布直方图.
(2)估计这次考试的及格率(60分及以上为及格),众数和中位数.(保留整数)
18、(9分)某行业主管部门为了解本行业中小企业的生产情况,随机调查了100个企业,得到这些企业第一季度相对于前一年第一季度产值增长率y的频数分布表。
y的分组
企业数 2 24 53 14 7
(1)分别估计这类企业中产值增长率不低于的企业比例、产值负增长的企业比例;
(2)求这类企业产值增长率的平均数与标准差的估计值(同一组中的数据用该组区间的中点值为代表)。(精确到)附:.
19、(9分)某学校随机抽取部分新生调查其上学所需时间(单位:分钟),并将所得数据绘制成频率分布直方图(如图).已知上学所需时间的范围是,样本数据分组为,,,,.
(1)求频率分布直方图中x的值;
(2)如果上学所需时间在的学生可申请在学校住宿,请估计该校800名新生中有多少名学生可以申请住宿.
参考答案
1、答案:B
解析:体重在内的频率为,体重在内的频率为,体重在内的频率为,
,
可估计该校初三学生适合参加跑步、跳远、投掷三项训练的集训人数之比为5:3:1.故选B.
2、答案:C
解析:由已知得数据,,…,的方差为.故选C.
3、答案:A
解析:由于去掉一个最高分与最低分后,评委所评的9个分数从小到大排序后,中间一个数字不会改变,故中位数不变.由于最高分和最低分是极端分数,因此会影响平均数、方差和极差.
4、答案:C
解析:由题中频率分布直方图可知,得分低于60分的频率为.低于60分的人数是18,该班的学生人数是.故选C.
5、答案:B
解析:初中部女教师有人,高中部女教师有人,所以该校女教师共有人.故选B.
6、答案:A
解析:,
,即.
年龄在,即内的职工有5人,
所以年龄在内的人数占公司总人数的百分比是.故选A.
7、答案:B
解析:设40个同学的数学成绩总分为z,则,且,由,得,所以.故选B.
8、答案:D
解析:设中间一组的频率为x,则其他8组的频率为,由题意知,解得,所以中间一组的频数为.故选D.
9、答案:B
解析:设该样本中的老年教师人数为x,由分层随机随机抽样的特点得,解得.故选B.
10、答案:C
解析:根据频率分布折线图,得折线的最高点对应的成绩是115,
据此估计此次考试成绩的众数是115.故选C.
11、答案:0.98
解析:依题意估计经停该站高铁列车所有车次的平均正点率的估计值为.
12、答案:2
解析:一组数据,,…,的方差是2,则,因此,即.①
又,,
.②
由①②联立,得,
解得或(不符合题意,舍去).
13、答案:3.6;1.4;B
解析:因为,,
所以,.
因为,所以B的射击成绩较稳定.
14、答案:
解析:因为,所以这组数据的第5个数50即为第60百分位数.观察易知这组数据的众数为50,所以a和b的大小关系是.
15、答案:4
解析:由题意,得
.,
.
16、答案:(1)0.0125(2)72(3)33.6 min
解析:(1)由频率分布直方图可得,解得.
(2)新生上学时间不少于1 h的频率为,
因为,
所以600名新生中约有72名学生可以申请住宿.
(3)由题可知.
故该校新生上学所需时间的平均值约为33.6 min.
17、答案:(1) 第四组的频率0.3,频率直方图见解析
(2)及格率75%;众数75,中位数约为73.3
解析:(1)因为各组的频率和等于1,故第四组的频率:,
补全频率分布直方图如图所示:
(2)依题意,60及以上的分数所在的第三、四、五、六组频率和为,所以抽样学生成绩的及格率是75%,
众数为最高小矩形底边的中点,是75;
由,知中位数在内,
设中位数为x,则,
解得;所以估计中位数是73.3分.
18、答案:(1)根据产值增长率频数分布表得,所调查的100个企业中产值增长率不低于的企业频率为。
产值负增长的企业频率为。
用样本频率分布估计总体分布得这类企业中产值增长率不低于的企业比例为,产值负增长的企业比例为。
(2),,。所以,这类企业产值增长率的平均数与标准差的估计值分别为。
解析:
19、答案:(1)
(2)800名新生中估计有96名学生可以申请住宿
解析:(1)由频率分布直方图可得到.
所以.
(2)由频率分布直方图可知,新生上学所需时间在的频率为,
所以估计全校新生上学所需时间在的概率为0.12.
因为,
所以800名新生中估计有96名学生可以申请住宿.
学校:___________姓名:___________班级:___________考号:___________
一、选择题(共40分)
1、(4分)某校为了对初三学生的体重进行摸底调查,随机抽取了50名学生的体重(kg),将所得数据整理后,画出了频率分布直方图.如图所示,体重在内适合跑步训练,体重在内适合跳远训练,体重在内适合投掷相关方面训练,估计该校初三学生适合参加跑步、跳远、投掷三项训练的集训人数之比为( )
A.4:3:1 B.5:3:1 C.5:3:2 D.3:2:1
2、(4分)设一组样本数据,,…,的方差为0.01,则数据,,…,的方差为( )
A.0.01 B.0.1 C.1 D.10
3、(4分)演讲比赛共有9位评委分别给出某选手的原始评分,评定该选手的成绩时,从9个原始评分中去掉1个最高分、1个最低分,得到7个有效评分.7个有效评分与9个原始评分相比,不变的数字特征是( )
A.中位数 B.平均数 C.方差 D.极差
4、(4分)某班全体学生参加一次测试,将所得分数依次分组:,,,,绘制出如图所示的成绩频率分布直方图.若低于60分的人数是18,则该班的学生人数是( )
A.50 B.54 C.60 D.64
5、(4分)某中学初中部共有120名教师,高中部共有150名教师,其性别比例如图所示,则该校女教师的人数为( )
A.128 B.144 C.174 D.167
6、(4分)某创业公司共有36名职工,为了了解该公司职工的年龄构成情况,随机采访了9名职工的年龄数据分别为36,36,37,37,44,40,43,44,43.若用样本估计总体,则年龄在内的人数占公司总人数的百分比是(精确到1%)( )
A.56% B.14% C.25% D.67%
7、(4分)期中考试后,班长算出了全班40个同学数学成绩的平均数为M.如果把M当成一个同学的分数,与原来的40个分数一起,算出这41个分数的平均数为N,那么为( )
A. B.1 C. D.2
8、(4分)在样本的频率分布直方图中,共有9个小长方形.若中间一个长方形的面积等于其他8个小长方形面积之和的,且样本量为200,则中间一组的频数为( )
A.0.2 B.0.25 C.40 D.50
9、(4分)某学校的教师配置比例如图所示,为了调查各类教师的薪资状况,现采用分层随机抽样的方法抽取部分教师进行调查.在抽取的样本中,青年教师30人,则该样本中的老年教师人数为( )
A.10 B.12 C.18 D.20
10、(4分)某同学将全班某次数学考试成绩整理成频率分布直方图后,并将每个小矩形上方线段的中点连接起来得到频率折线图(如图所示),据此估计此次考试成绩的众数是( )
A.100 B.110 C.115 D.120
二、填空题(共25分)
11、(5分)我国高铁发展迅速,技术先进.经统计,在经停某站的高铁列车中,有10个车次的正点率为0.97,有20个车次的正点率为0.98,有10个车次的正点率为0.99,则经停该站高铁列车所有车次的平均正点率的估计值为_____________.
12、(5分)已知一组数据,,…,的方差是2,并且,,则_____________.
13、(5分)A,B两人各射击10次,命中环数如下:
A:8 6 9 5 10 7 4 7 9 5;
B:7 6 5 8 6 9 6 8 8 7.
A,B两人的方差分别为_________、_________,由以上计算可得_________的射击成绩较稳定.
14、(5分)已知一组数据:20,30,40,50,50,60,70,80,记这组数据的第60百分位数为a,众数为b,则a和b的大小关系是___________________.(用“<”“>”或“=”连接)
15、(5分)某人5次上班途中所花的时间(单位:分)分别为x,y,10,11,9.已知这组数据的平均数为10,方差为2,则的值为__________.
三、解答题(共35分)
16、(8分)某学校随机抽取部分新生调查其上学所需时间(单位:min),并将所得数据绘制成频率分布直方图(如图),其中上学所需时间的范围是,样本数据分组为,,,,.
(1)求频率分布直方图中x的值;
(2)假设上学所需时间不少于1 h的学生可申请在学校住宿,若该学校有600名新生,请估计新生中有多少名学生可以申请住宿;
(3)由频率分布直方图估计该校新生上学所需时间的平均值.
17、(9分)某校从参加高一年级期末考试的学生中抽出60名学生,将其成绩(均为整数)分成六段后画出如图部分频率分布直方图.观察图形的信息,回答下列问题:
(1)求第四小组的频率,并补全这个频率分布直方图.
(2)估计这次考试的及格率(60分及以上为及格),众数和中位数.(保留整数)
18、(9分)某行业主管部门为了解本行业中小企业的生产情况,随机调查了100个企业,得到这些企业第一季度相对于前一年第一季度产值增长率y的频数分布表。
y的分组
企业数 2 24 53 14 7
(1)分别估计这类企业中产值增长率不低于的企业比例、产值负增长的企业比例;
(2)求这类企业产值增长率的平均数与标准差的估计值(同一组中的数据用该组区间的中点值为代表)。(精确到)附:.
19、(9分)某学校随机抽取部分新生调查其上学所需时间(单位:分钟),并将所得数据绘制成频率分布直方图(如图).已知上学所需时间的范围是,样本数据分组为,,,,.
(1)求频率分布直方图中x的值;
(2)如果上学所需时间在的学生可申请在学校住宿,请估计该校800名新生中有多少名学生可以申请住宿.
参考答案
1、答案:B
解析:体重在内的频率为,体重在内的频率为,体重在内的频率为,
,
可估计该校初三学生适合参加跑步、跳远、投掷三项训练的集训人数之比为5:3:1.故选B.
2、答案:C
解析:由已知得数据,,…,的方差为.故选C.
3、答案:A
解析:由于去掉一个最高分与最低分后,评委所评的9个分数从小到大排序后,中间一个数字不会改变,故中位数不变.由于最高分和最低分是极端分数,因此会影响平均数、方差和极差.
4、答案:C
解析:由题中频率分布直方图可知,得分低于60分的频率为.低于60分的人数是18,该班的学生人数是.故选C.
5、答案:B
解析:初中部女教师有人,高中部女教师有人,所以该校女教师共有人.故选B.
6、答案:A
解析:,
,即.
年龄在,即内的职工有5人,
所以年龄在内的人数占公司总人数的百分比是.故选A.
7、答案:B
解析:设40个同学的数学成绩总分为z,则,且,由,得,所以.故选B.
8、答案:D
解析:设中间一组的频率为x,则其他8组的频率为,由题意知,解得,所以中间一组的频数为.故选D.
9、答案:B
解析:设该样本中的老年教师人数为x,由分层随机随机抽样的特点得,解得.故选B.
10、答案:C
解析:根据频率分布折线图,得折线的最高点对应的成绩是115,
据此估计此次考试成绩的众数是115.故选C.
11、答案:0.98
解析:依题意估计经停该站高铁列车所有车次的平均正点率的估计值为.
12、答案:2
解析:一组数据,,…,的方差是2,则,因此,即.①
又,,
.②
由①②联立,得,
解得或(不符合题意,舍去).
13、答案:3.6;1.4;B
解析:因为,,
所以,.
因为,所以B的射击成绩较稳定.
14、答案:
解析:因为,所以这组数据的第5个数50即为第60百分位数.观察易知这组数据的众数为50,所以a和b的大小关系是.
15、答案:4
解析:由题意,得
.,
.
16、答案:(1)0.0125(2)72(3)33.6 min
解析:(1)由频率分布直方图可得,解得.
(2)新生上学时间不少于1 h的频率为,
因为,
所以600名新生中约有72名学生可以申请住宿.
(3)由题可知.
故该校新生上学所需时间的平均值约为33.6 min.
17、答案:(1) 第四组的频率0.3,频率直方图见解析
(2)及格率75%;众数75,中位数约为73.3
解析:(1)因为各组的频率和等于1,故第四组的频率:,
补全频率分布直方图如图所示:
(2)依题意,60及以上的分数所在的第三、四、五、六组频率和为,所以抽样学生成绩的及格率是75%,
众数为最高小矩形底边的中点,是75;
由,知中位数在内,
设中位数为x,则,
解得;所以估计中位数是73.3分.
18、答案:(1)根据产值增长率频数分布表得,所调查的100个企业中产值增长率不低于的企业频率为。
产值负增长的企业频率为。
用样本频率分布估计总体分布得这类企业中产值增长率不低于的企业比例为,产值负增长的企业比例为。
(2),,。所以,这类企业产值增长率的平均数与标准差的估计值分别为。
解析:
19、答案:(1)
(2)800名新生中估计有96名学生可以申请住宿
解析:(1)由频率分布直方图可得到.
所以.
(2)由频率分布直方图可知,新生上学所需时间在的频率为,
所以估计全校新生上学所需时间在的概率为0.12.
因为,
所以800名新生中估计有96名学生可以申请住宿.
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
