1.2.4 绝对值 课件(共20张PPT)
文档属性
| 名称 | 1.2.4 绝对值 课件(共20张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-23 15:05:19 | ||
图片预览







文档简介
(共20张PPT)
人教版 七年级上册
1.2.4 绝对值
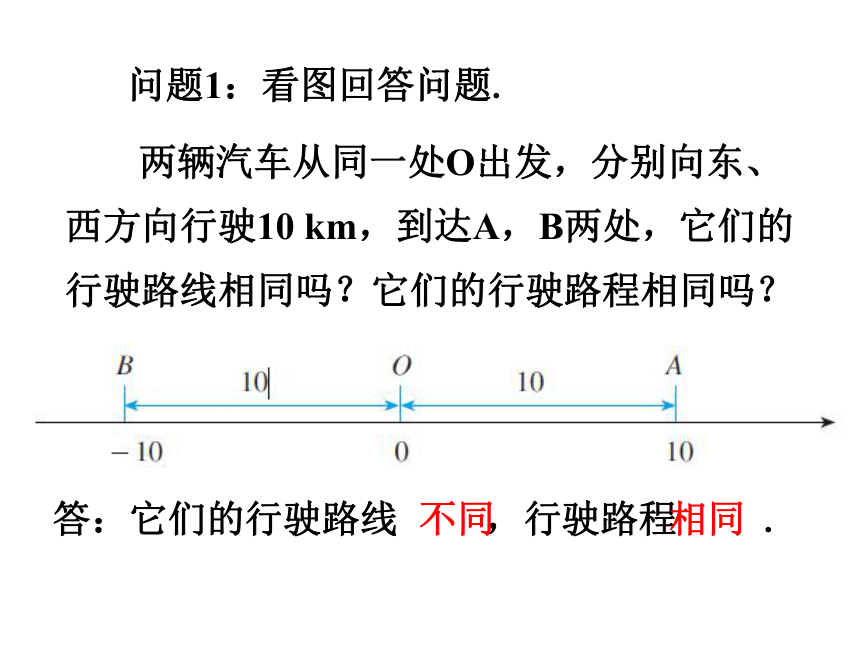
问题1:看图回答问题.
两辆汽车从同一处O出发,分别向东、西方向行驶10 km,到达A,B两处,它们的行驶路线相同吗?它们的行驶路程相同吗?
答:它们的行驶路线 ,行驶路程 .
不同
相同
在数轴上,表示-3的点到原点的距离是 表示3的点到原点的距离是 所以-3 和3到原点的距离都是
观察下面数轴上的点,表示-3的点到原点的距离是多少?表示3的点呢?-2和2呢?
在数轴上,表示-2的点到原点的距离是 表示2的点到原点的距离是 所以-2 和2到原点的距离都是
3,
3.
3,
2,
2,
2.
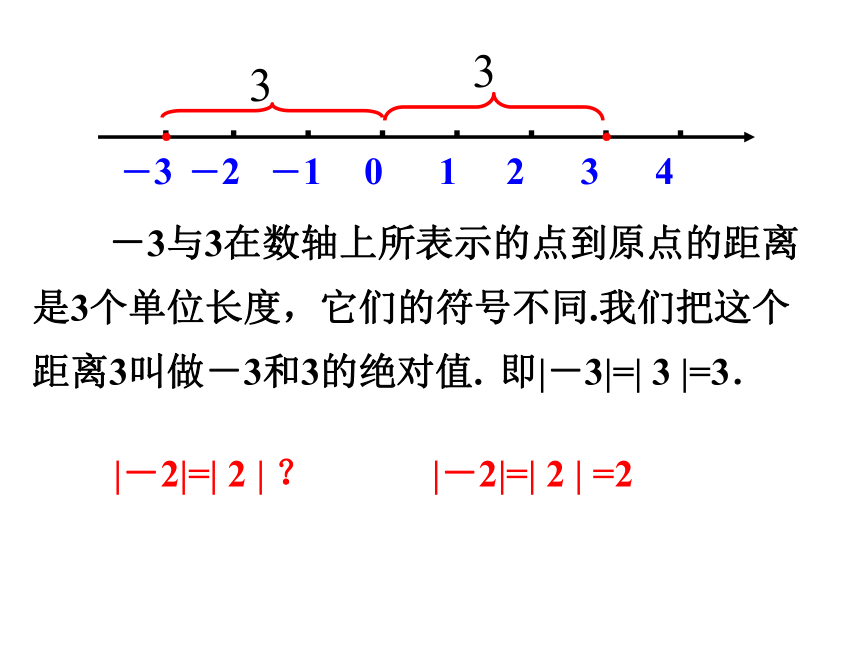
-3与3在数轴上所表示的点到原点的距离是3个单位长度,它们的符号不同.我们把这个距离3叫做-3和3的绝对值.
3
3
0
1
2
3
4
-1
-2
-3
●
●
即|-3|=| 3 |=3.
|-2|=| 2 | ?
|-2|=| 2 | =2
一般地,数轴上表示数a的点与原点的距离叫做数a的绝对值,记作 .
例如数轴上表示-3的点到原点的距离是3,所以-3的绝对值可记为|-3|.即|-3|=3.
例如数轴上表示4的点到原点的距离是4,所以4的绝对值可记为| 4 |.
即| 4 |=4.
绝对值:
绝对值的定义:
| a |
1.-5的绝对值是____,说明数轴上表示-5
的点到 的距离是____个单位长度.
2.-0.8的绝对值是____ .
问题2:练习,讨论,归纳.
5
原点
5
0.8
3.口答:
问题2:练习,讨论,归纳.
6
0
3
8.2
| +6 |=
| |=
| 8.2 |=
| 0 |=
| -3 |=
|- |=
1
3
1
3
2
7
2
7
数a的绝对值的一般规律:
(1)一个正数的绝对值是它本身;
(2)一个负数的绝对值是它的相反数;
(3)0的绝对值是0.
问题3:结合上面口答题结果,你能从中发现什么规律?
即:①若a>0,则| a |
②若a<0,则| a |
③若a=0, 则| a |
=a
=-a
=0.
问题4:小组讨论下面3个问题:
(1)有没有绝对值等于-2的数?
(2)一个数的绝对值会是负数吗?为什么?
(3)不论有理数a取何值,它的绝对值总是
什么数?
不论有理数a取何值,它的绝对值总是正数或0(非负数).
即对任意有理数a,总有
≥0.
| a |
问题5:互为相反数的两个数的绝对值有什么关系?
观察:一对相反数虽然分别在原点两边,但它们到原点的距离是相等的.
结论:互为相反数的两个数的绝对值相等.
1.写出下列各数的绝对值:
6,-8,-3.9, , ,100 ,0 .
解:
8 ,
100,
0.
6 ,
3.9,
练习巩固
5
2
-
2
11
| 6 |=
| - 8 |=
| - 3.9 |=
| |=
5
2
5
2
| |=
-
2
11
2
11
| 100 |=
| 0 |=
2.判断下列说法是否正确:
(1)符号相反的数是相反数;
(3)一个数的绝对值越大,表示它的点在数轴
上离原点越远;
(4)当a≠0时, 总是大于0.
(2)一个数的绝对值越大,表示它的点在数轴
上越靠右;
解:
(4)正确.
(3)正确,
(2)错,
(1)错,
3.判断下列各式是否正确:
解:
(1)正确,
(2)错误,
(3)错误.
5.计算:
(1)|-3|×|-5.2|; (2)|-5|+|1.49|;
4.-2的绝对值是 ;绝对值是2的数是 .
2
2或-2
±2
5.计算:
(1)|-3|×|-5.2|; (2)|-5|+|1.49|;
(1)原式=
解:
(2)原式=
(3)原式=
(4)原式=
=6.49
=15.6
3×5.2
5+1.49
=0
=11
1.求有理数的绝对值;
2.已知绝对值求数;
3.利用绝对值解决实际问题.
课堂小结
1. 绝对值等于相反数的数一定是( ).
A.负数 B.正数
C.负数或零 D.正数和零
2.下面四个结论中,正确的是( ).
A.|- 2|>|-3| B.|2|>|3|
C.2>|-3| D.2<| -3|
C
D
巩固提高
3. 若|-22|=| x |,则x= .
22
或-22
教科书习题1.2 第5,10,12题.
课后作业:
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
人教版 七年级上册
1.2.4 绝对值
问题1:看图回答问题.
两辆汽车从同一处O出发,分别向东、西方向行驶10 km,到达A,B两处,它们的行驶路线相同吗?它们的行驶路程相同吗?
答:它们的行驶路线 ,行驶路程 .
不同
相同
在数轴上,表示-3的点到原点的距离是 表示3的点到原点的距离是 所以-3 和3到原点的距离都是
观察下面数轴上的点,表示-3的点到原点的距离是多少?表示3的点呢?-2和2呢?
在数轴上,表示-2的点到原点的距离是 表示2的点到原点的距离是 所以-2 和2到原点的距离都是
3,
3.
3,
2,
2,
2.
-3与3在数轴上所表示的点到原点的距离是3个单位长度,它们的符号不同.我们把这个距离3叫做-3和3的绝对值.
3
3
0
1
2
3
4
-1
-2
-3
●
●
即|-3|=| 3 |=3.
|-2|=| 2 | ?
|-2|=| 2 | =2
一般地,数轴上表示数a的点与原点的距离叫做数a的绝对值,记作 .
例如数轴上表示-3的点到原点的距离是3,所以-3的绝对值可记为|-3|.即|-3|=3.
例如数轴上表示4的点到原点的距离是4,所以4的绝对值可记为| 4 |.
即| 4 |=4.
绝对值:
绝对值的定义:
| a |
1.-5的绝对值是____,说明数轴上表示-5
的点到 的距离是____个单位长度.
2.-0.8的绝对值是____ .
问题2:练习,讨论,归纳.
5
原点
5
0.8
3.口答:
问题2:练习,讨论,归纳.
6
0
3
8.2
| +6 |=
| |=
| 8.2 |=
| 0 |=
| -3 |=
|- |=
1
3
1
3
2
7
2
7
数a的绝对值的一般规律:
(1)一个正数的绝对值是它本身;
(2)一个负数的绝对值是它的相反数;
(3)0的绝对值是0.
问题3:结合上面口答题结果,你能从中发现什么规律?
即:①若a>0,则| a |
②若a<0,则| a |
③若a=0, 则| a |
=a
=-a
=0.
问题4:小组讨论下面3个问题:
(1)有没有绝对值等于-2的数?
(2)一个数的绝对值会是负数吗?为什么?
(3)不论有理数a取何值,它的绝对值总是
什么数?
不论有理数a取何值,它的绝对值总是正数或0(非负数).
即对任意有理数a,总有
≥0.
| a |
问题5:互为相反数的两个数的绝对值有什么关系?
观察:一对相反数虽然分别在原点两边,但它们到原点的距离是相等的.
结论:互为相反数的两个数的绝对值相等.
1.写出下列各数的绝对值:
6,-8,-3.9, , ,100 ,0 .
解:
8 ,
100,
0.
6 ,
3.9,
练习巩固
5
2
-
2
11
| 6 |=
| - 8 |=
| - 3.9 |=
| |=
5
2
5
2
| |=
-
2
11
2
11
| 100 |=
| 0 |=
2.判断下列说法是否正确:
(1)符号相反的数是相反数;
(3)一个数的绝对值越大,表示它的点在数轴
上离原点越远;
(4)当a≠0时, 总是大于0.
(2)一个数的绝对值越大,表示它的点在数轴
上越靠右;
解:
(4)正确.
(3)正确,
(2)错,
(1)错,
3.判断下列各式是否正确:
解:
(1)正确,
(2)错误,
(3)错误.
5.计算:
(1)|-3|×|-5.2|; (2)|-5|+|1.49|;
4.-2的绝对值是 ;绝对值是2的数是 .
2
2或-2
±2
5.计算:
(1)|-3|×|-5.2|; (2)|-5|+|1.49|;
(1)原式=
解:
(2)原式=
(3)原式=
(4)原式=
=6.49
=15.6
3×5.2
5+1.49
=0
=11
1.求有理数的绝对值;
2.已知绝对值求数;
3.利用绝对值解决实际问题.
课堂小结
1. 绝对值等于相反数的数一定是( ).
A.负数 B.正数
C.负数或零 D.正数和零
2.下面四个结论中,正确的是( ).
A.|- 2|>|-3| B.|2|>|3|
C.2>|-3| D.2<| -3|
C
D
巩固提高
3. 若|-22|=| x |,则x= .
22
或-22
教科书习题1.2 第5,10,12题.
课后作业:
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
