1.2.5 比较有理数的大小 课件(共25张PPT)
文档属性
| 名称 | 1.2.5 比较有理数的大小 课件(共25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 940.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-23 15:06:27 | ||
图片预览





文档简介
(共25张PPT)
人教版 七年级上册
1.2.5 比较有理数的大小
教学目标
会借助数轴,理解有理数大小关系,能
比较两个有理数的大小.
通过两个负数大小比较的推理分析,培养
学生良好的思维能力.也认识到生活是学好数
学的源泉.
教学重点:运用法则或借助数轴比较两个有理数的大小.
教学难点:比较两个负数的大小.
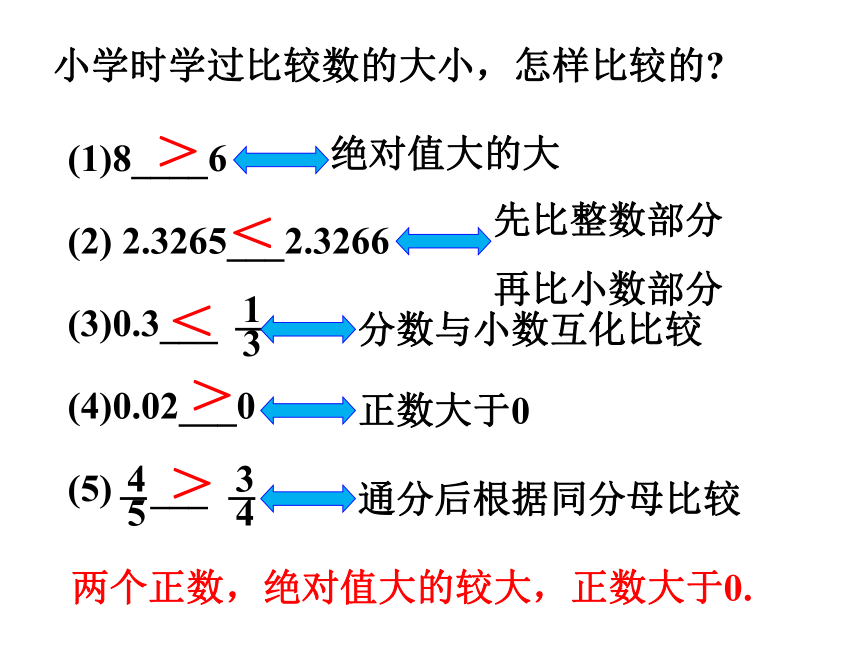
(1)8____6
(2) 2.3265___2.3266
(3)0.3___
(4)0.02___0
(5) ___
小学时学过比较数的大小,怎样比较的
绝对值大的大
正数大于0
通分后根据同分母比较
先比整数部分
再比小数部分
分数与小数互化比较
>
<
<
>
>
两个正数,绝对值大的较大,正数大于0.
1
3
4
5
3
4
观察下列数,你会比较他们的大小吗?
负数和负数
正数和负数
负数和0
正数和0
-6___-8
5____-7
-2_____0
2_____0
学习新知
下图表示某一天我国5个城市的最低气温.
武汉5 ℃ 北京-10℃ 上海0℃ 广州10℃ 哈尔滨-20℃
问:你能将上述五个城市的最低气温按从低到高的顺序依次排列吗?
哈尔滨
-20℃
北京
-10℃
上海
0℃
武汉
5℃
广州
10℃
<
<
<
<
探究新知
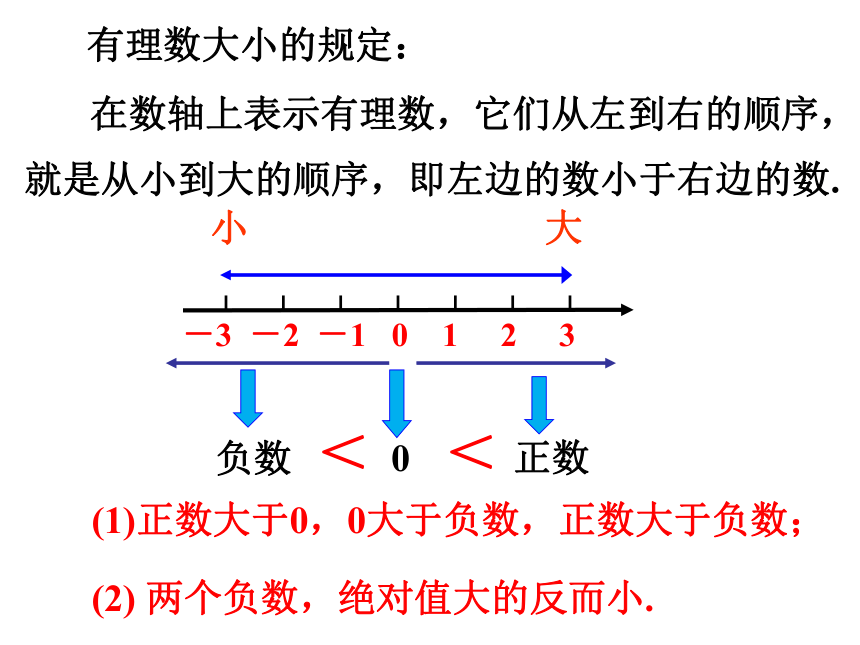
在数轴上表示有理数,它们从左到右的顺序,就是从小到大的顺序,即左边的数小于右边的数.
小 大
-3 -2 -1 0 1 2 3
有理数大小的规定:
负数
0
正数
<
<
(1)正数大于0,0大于负数,正数大于负数;
(2) 两个负数,绝对值大的反而小.
(1)正数大于0,0大于负数,正数大于负数;
(2) 两个负数,绝对值大的反而小.
有理数大小的规定:
如:1 0;0 -1;1 -1;-1 -2.
>
>
>
>
用“<”,“>”,“=”连接下面的数.
3___-4; 5___0;
-7 ___0; -3 ___-|-3|;
-|-7| ___0; |2| ___-2.
<
>
=
>
>
<
课堂练习
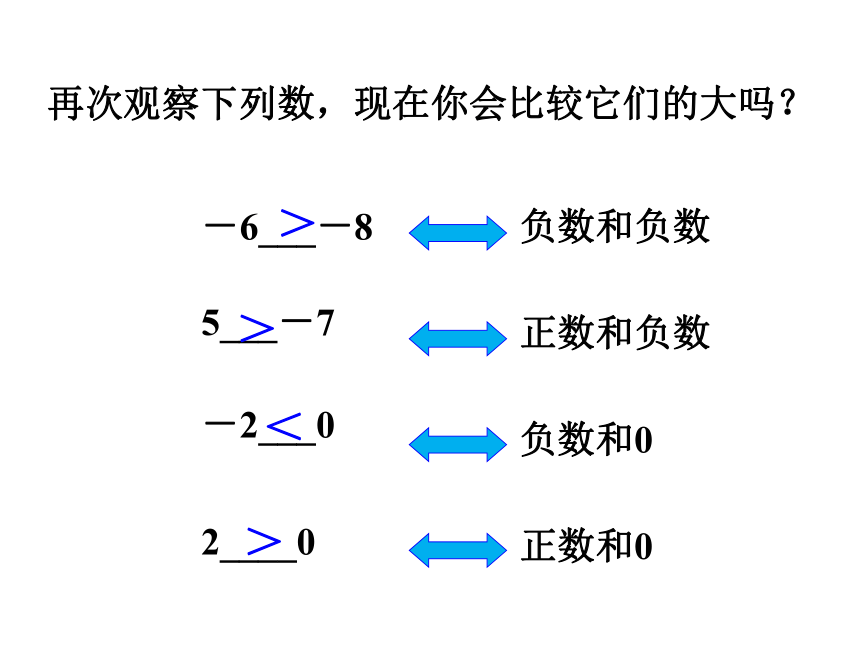
负数和负数
正数和负数
负数和0
正数和0
-6___-8
5___-7
-2___0
2____0
再次观察下列数,现在你会比较它们的大吗?
>
>
<
>
例
比较下列各对数的大小:
(1)- (-1)和- (+2);
(2)- 和- ;
3
7
8
21
(3) - (-0.3)和 .
| - |
1
3
例题解析
解: (1)先化简,- (-1)=1,
- (+2)=-2,
因为正数大于负数,所以1>-2,即
-(-1) >-(+2);
(1)- (-1)和- (+2);
所以- - .
(2)两个负数做比较,先求它们的绝对值.
<
<
(2)- 和- ;
3
7
8
21
|- |=
3
7
3
7
9
21
= ,
8
21
9
21
|- |
8
21
|- | ,
3
7
3
7
8
21
>
所以
| - |= ,
8
21
8
21
因为
(3)先化简:
(3) - (-0.3)和 .
| - |=
1
3
因为
1
3
≈0.33,
| - |
1
3
- (-0.3)=0.3
0.33>0.3,
所以
所以- (-0.3) < .
| - |
1
3
1
3
>0.3,
练习
比较下列各对数的大小:
(1)3和-5;
(2) -3和-5;
(3)-2.5和-
|-2.25|;
解:
(1)3>-5;
(2) -3>-5;
(3)因为 |-2. 5|=2.5,
|-2.25|=2.25,
2.5>2.25;
所以 |-2. 5|>
|-2.25|,
所以-2.5 -
|-2.25|;
<
(4) - 和- .
3
5
3
4
(4)因为
|- |=
3
5
3
5
=0.6,
| - |=
3
4
3
4
=0.75,
0.6<0.75,
所以
|- |<
3
5
|- |,
3
4
所以
- >- .
3
5
3
4
我们这节课学到了什么?
比较有理数大小的方法
数轴法:
在数轴上表示的两个数,右边的数总比左边的大.
规律:
(1)正数都大于0,负数都 小 于0,
正数大于一切负数.
(2)两个负数,绝对值大的反而小.
课堂小结
任意几个数比较大小方法:
(1)按照负数<0,0<正数,负数<正数的规定比较;
(2)在数轴上找出每个数,观察它们从左到右的顺序.
1.将下列这些数按从小到大的顺序排列,并用<连接.
0;-3,|5|,- (-4),-|-5|.
-|-5|< -3 <0< - (-4)<|5|.
解:
堂上练习
2.如果一个数的绝对值等于4.53 ,则这个数是_______________.
3.如果a 的相反数是-0.86,那|a|=______.
4.53或-4.53
0.86
4.下列各式中,不正确的是 ( ).
A.︱-0.2︱>-0.2
B.-︱-0.2︱<-(-0.2)
C.-︱-0.2︱>一0.2
D.︱-0.2︱>-︱-0.2︱
C
5.若有理数a,b在数轴上的对应点位置如图
所示,则下列结论中正确的是( ).
A.b>a B.│a│>-b
C.│b│>a D.│a│>│b│
-2 -1 0 1
a
b
C
6.下列说法正确的是 ( ).
A.有理数的绝对值一定是正数;
B.如果两个数的绝对值相等,那么这两个
数相等;
C.符号相反且绝对值相等的数互为相反数;
D.一个数的绝对值越大,表示它的点在数轴
上离原点越近.
C
7.不小于-4,而小于4的整数有( ).
A.6个 B.7个
C.8个 D.9个
C
8.下列结论中正确的是( ).
A.若m<n,则│m│<│n│.
B.若│m│=│n│,则m=n.
C.若m≠n,则│m│≠│n│.
D.若m<n<0,则│m│>│n│.
D
教科书习题1.2 第6,11题.
课后作业:
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
人教版 七年级上册
1.2.5 比较有理数的大小
教学目标
会借助数轴,理解有理数大小关系,能
比较两个有理数的大小.
通过两个负数大小比较的推理分析,培养
学生良好的思维能力.也认识到生活是学好数
学的源泉.
教学重点:运用法则或借助数轴比较两个有理数的大小.
教学难点:比较两个负数的大小.
(1)8____6
(2) 2.3265___2.3266
(3)0.3___
(4)0.02___0
(5) ___
小学时学过比较数的大小,怎样比较的
绝对值大的大
正数大于0
通分后根据同分母比较
先比整数部分
再比小数部分
分数与小数互化比较
>
<
<
>
>
两个正数,绝对值大的较大,正数大于0.
1
3
4
5
3
4
观察下列数,你会比较他们的大小吗?
负数和负数
正数和负数
负数和0
正数和0
-6___-8
5____-7
-2_____0
2_____0
学习新知
下图表示某一天我国5个城市的最低气温.
武汉5 ℃ 北京-10℃ 上海0℃ 广州10℃ 哈尔滨-20℃
问:你能将上述五个城市的最低气温按从低到高的顺序依次排列吗?
哈尔滨
-20℃
北京
-10℃
上海
0℃
武汉
5℃
广州
10℃
<
<
<
<
探究新知
在数轴上表示有理数,它们从左到右的顺序,就是从小到大的顺序,即左边的数小于右边的数.
小 大
-3 -2 -1 0 1 2 3
有理数大小的规定:
负数
0
正数
<
<
(1)正数大于0,0大于负数,正数大于负数;
(2) 两个负数,绝对值大的反而小.
(1)正数大于0,0大于负数,正数大于负数;
(2) 两个负数,绝对值大的反而小.
有理数大小的规定:
如:1 0;0 -1;1 -1;-1 -2.
>
>
>
>
用“<”,“>”,“=”连接下面的数.
3___-4; 5___0;
-7 ___0; -3 ___-|-3|;
-|-7| ___0; |2| ___-2.
<
>
=
>
>
<
课堂练习
负数和负数
正数和负数
负数和0
正数和0
-6___-8
5___-7
-2___0
2____0
再次观察下列数,现在你会比较它们的大吗?
>
>
<
>
例
比较下列各对数的大小:
(1)- (-1)和- (+2);
(2)- 和- ;
3
7
8
21
(3) - (-0.3)和 .
| - |
1
3
例题解析
解: (1)先化简,- (-1)=1,
- (+2)=-2,
因为正数大于负数,所以1>-2,即
-(-1) >-(+2);
(1)- (-1)和- (+2);
所以- - .
(2)两个负数做比较,先求它们的绝对值.
<
<
(2)- 和- ;
3
7
8
21
|- |=
3
7
3
7
9
21
= ,
8
21
9
21
|- |
8
21
|- | ,
3
7
3
7
8
21
>
所以
| - |= ,
8
21
8
21
因为
(3)先化简:
(3) - (-0.3)和 .
| - |=
1
3
因为
1
3
≈0.33,
| - |
1
3
- (-0.3)=0.3
0.33>0.3,
所以
所以- (-0.3) < .
| - |
1
3
1
3
>0.3,
练习
比较下列各对数的大小:
(1)3和-5;
(2) -3和-5;
(3)-2.5和-
|-2.25|;
解:
(1)3>-5;
(2) -3>-5;
(3)因为 |-2. 5|=2.5,
|-2.25|=2.25,
2.5>2.25;
所以 |-2. 5|>
|-2.25|,
所以-2.5 -
|-2.25|;
<
(4) - 和- .
3
5
3
4
(4)因为
|- |=
3
5
3
5
=0.6,
| - |=
3
4
3
4
=0.75,
0.6<0.75,
所以
|- |<
3
5
|- |,
3
4
所以
- >- .
3
5
3
4
我们这节课学到了什么?
比较有理数大小的方法
数轴法:
在数轴上表示的两个数,右边的数总比左边的大.
规律:
(1)正数都大于0,负数都 小 于0,
正数大于一切负数.
(2)两个负数,绝对值大的反而小.
课堂小结
任意几个数比较大小方法:
(1)按照负数<0,0<正数,负数<正数的规定比较;
(2)在数轴上找出每个数,观察它们从左到右的顺序.
1.将下列这些数按从小到大的顺序排列,并用<连接.
0;-3,|5|,- (-4),-|-5|.
-|-5|< -3 <0< - (-4)<|5|.
解:
堂上练习
2.如果一个数的绝对值等于4.53 ,则这个数是_______________.
3.如果a 的相反数是-0.86,那|a|=______.
4.53或-4.53
0.86
4.下列各式中,不正确的是 ( ).
A.︱-0.2︱>-0.2
B.-︱-0.2︱<-(-0.2)
C.-︱-0.2︱>一0.2
D.︱-0.2︱>-︱-0.2︱
C
5.若有理数a,b在数轴上的对应点位置如图
所示,则下列结论中正确的是( ).
A.b>a B.│a│>-b
C.│b│>a D.│a│>│b│
-2 -1 0 1
a
b
C
6.下列说法正确的是 ( ).
A.有理数的绝对值一定是正数;
B.如果两个数的绝对值相等,那么这两个
数相等;
C.符号相反且绝对值相等的数互为相反数;
D.一个数的绝对值越大,表示它的点在数轴
上离原点越近.
C
7.不小于-4,而小于4的整数有( ).
A.6个 B.7个
C.8个 D.9个
C
8.下列结论中正确的是( ).
A.若m<n,则│m│<│n│.
B.若│m│=│n│,则m=n.
C.若m≠n,则│m│≠│n│.
D.若m<n<0,则│m│>│n│.
D
教科书习题1.2 第6,11题.
课后作业:
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
