六年级上册数学人教版第5单元《圆的面积》 学案(含答案)
文档属性
| 名称 | 六年级上册数学人教版第5单元《圆的面积》 学案(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 101.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-22 13:56:53 | ||
图片预览


文档简介
圆的面积
班级: 组别: 组号: 姓名:
圆环的面积
预习要求
预习书本第68页,并把例题补充完整。
认识圆环,能运用圆环面积的计算公式灵活解决实际问题。
【课前热身】
1.回顾旧知
(1)一个圆的直径是1米,它的面积是多少平方米?
(2)一个圆的周长是1.256米,那么它的面积是多少平方米?
【合作探究】
1.探一探
(1)画一画,剪一剪,找一找。
A.以O为圆心,画一个半径5厘米的圆。
B.以刚才的圆心为圆心,画一个半径3厘米的圆。
C.把里面的那个半径为3厘米的圆剪下来,剩下的部分我们称它为圆环。
D.在我们生活中,你在哪里见过圆环?(找一找,写下来)
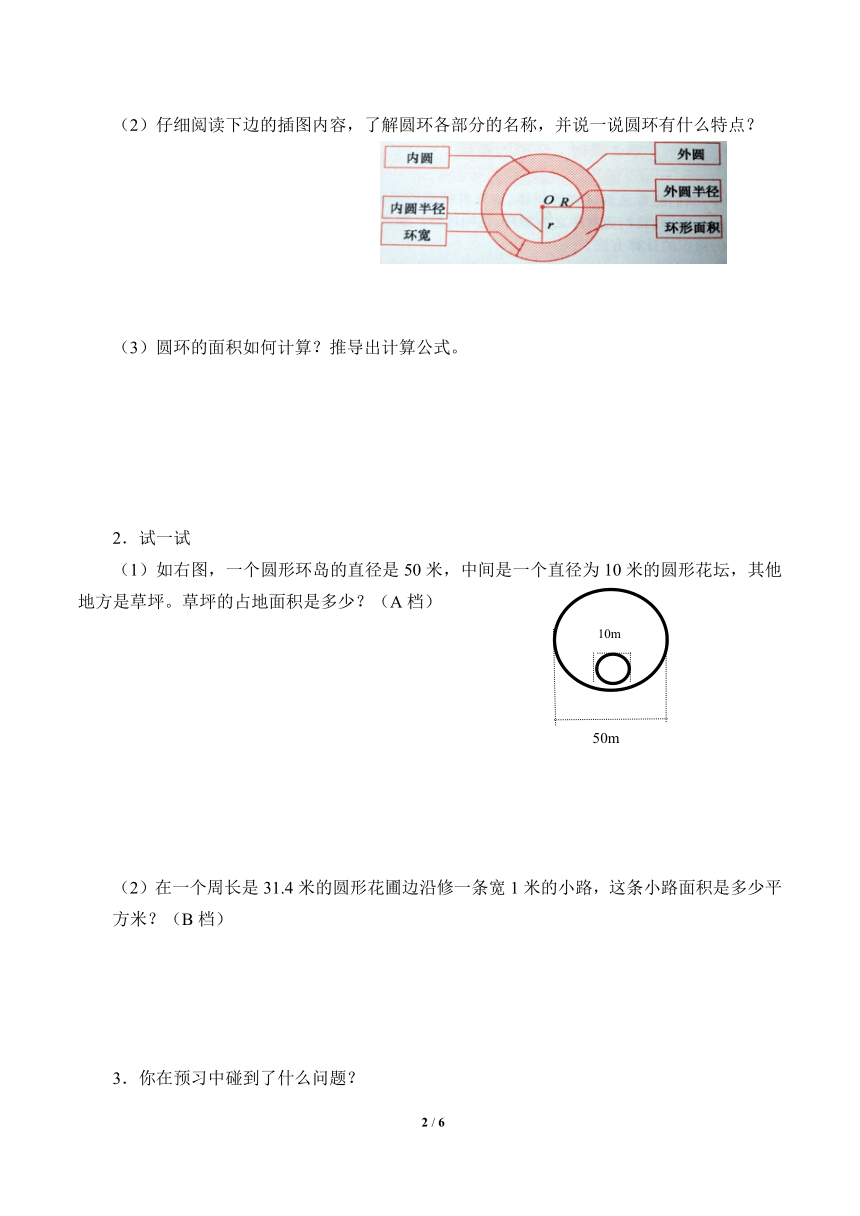
(2)仔细阅读下边的插图内容,了解圆环各部分的名称,并说一说圆环有什么特点?
(3)圆环的面积如何计算?推导出计算公式。
2.试一试
(1)如右图,一个圆形环岛的直径是50米,中间是一个直径为10米的圆形花坛,其他地方是草坪。草坪的占地面积是多少?(A档)
(2)在一个周长是31.4米的圆形花圃边沿修一条宽1米的小路,这条小路面积是多少平方米?(B档)
3.你在预习中碰到了什么问题?
4.小结。
(1)圆环
(2)优化圆环面积公式
【精练反馈】
1.完成书P73第12题(A档)
圭峰楼外半径:
圭峰楼内半径:
德逊楼外半径:
德逊楼内半径:
圭峰楼占地面积:
德逊楼占地面积:
2.求阴影部分的面积。(B档)
3.完成书P72第7题(B档)
【课堂小结】
通过今天这节课的学习,你有什么新的收获或你有什么疑问?
【拓展延伸】(C档)
张红用一张边长为10厘米的正方形纸片剪了4片树叶(如图)
(1)请你像右边一样剪一剪。
(2)求出所得树叶的周长。
(3)求树叶的面积。
【易错收集】
【答案】
【课前热身】
1.(1)S=πr =3.14×(1÷2)2=3.14×0.25=0.785(平方米)
(2)r:1.256÷(2×3.14)=0.2(m) S=πr =3.14×0.22=0.1256(m )答:略
【合作探究】
1.(1)略
(2)特点:两个同心圆。
(3)圆环面积=外圆面积-内圆面积
2.(1)R:50÷2=25(m) r:10÷2=5(m)
S=π(R2-r2)=3.14×(25×25-5×5)=3.14×600=1884(m ) 答:略
(2)r:31.4÷6.28=5(米) R:5+1=6(米)
3.14×(6×6)-3.14×(5×5)=3.14×36-3.14×25=34.54(平方米) 答:略
3.略
4.略
【精练反馈】
1.33÷2=16.5(米)
14÷2=7(米)
26.4÷2=13.2(米)
14.4÷2=7.2(米)
3.14×(16.5×16.5-7×7)=701.005(平方米)
3.14×(13.2×13.2-7.2×7.2)=384.336(平方米)
701.005-384.336=316.669(平方米)
答:略
2.大圆半径:2+2=4
小圆半径:4÷2=2
3.14×(4×4-2×2)=3.14×12=37.86
37.86÷2=18.84
答:略
3.(1)大圆半径:12÷2=6(cm)
小圆半径:8÷2=4(cm)3.14×(6+4)=3.14×10=31.4(cm)
12-8=4(cm) 31.4+4=35.4(cm)
答:略
(2)3.14×(12×12-8×8)=3.14×80=251.2(m )答:略
【课堂小结】略
【拓展延伸】
(1)略
(2)3.14×10×2=62.8(cm)
(3)3.14×(10÷2)×(10÷2)=78.5(cm ) 78.5×2=157(cm )
10×10=100(cm )157-100=57(cm )答:略
【易错收集】略
5 / 6
班级: 组别: 组号: 姓名:
圆环的面积
预习要求
预习书本第68页,并把例题补充完整。
认识圆环,能运用圆环面积的计算公式灵活解决实际问题。
【课前热身】
1.回顾旧知
(1)一个圆的直径是1米,它的面积是多少平方米?
(2)一个圆的周长是1.256米,那么它的面积是多少平方米?
【合作探究】
1.探一探
(1)画一画,剪一剪,找一找。
A.以O为圆心,画一个半径5厘米的圆。
B.以刚才的圆心为圆心,画一个半径3厘米的圆。
C.把里面的那个半径为3厘米的圆剪下来,剩下的部分我们称它为圆环。
D.在我们生活中,你在哪里见过圆环?(找一找,写下来)
(2)仔细阅读下边的插图内容,了解圆环各部分的名称,并说一说圆环有什么特点?
(3)圆环的面积如何计算?推导出计算公式。
2.试一试
(1)如右图,一个圆形环岛的直径是50米,中间是一个直径为10米的圆形花坛,其他地方是草坪。草坪的占地面积是多少?(A档)
(2)在一个周长是31.4米的圆形花圃边沿修一条宽1米的小路,这条小路面积是多少平方米?(B档)
3.你在预习中碰到了什么问题?
4.小结。
(1)圆环
(2)优化圆环面积公式
【精练反馈】
1.完成书P73第12题(A档)
圭峰楼外半径:
圭峰楼内半径:
德逊楼外半径:
德逊楼内半径:
圭峰楼占地面积:
德逊楼占地面积:
2.求阴影部分的面积。(B档)
3.完成书P72第7题(B档)
【课堂小结】
通过今天这节课的学习,你有什么新的收获或你有什么疑问?
【拓展延伸】(C档)
张红用一张边长为10厘米的正方形纸片剪了4片树叶(如图)
(1)请你像右边一样剪一剪。
(2)求出所得树叶的周长。
(3)求树叶的面积。
【易错收集】
【答案】
【课前热身】
1.(1)S=πr =3.14×(1÷2)2=3.14×0.25=0.785(平方米)
(2)r:1.256÷(2×3.14)=0.2(m) S=πr =3.14×0.22=0.1256(m )答:略
【合作探究】
1.(1)略
(2)特点:两个同心圆。
(3)圆环面积=外圆面积-内圆面积
2.(1)R:50÷2=25(m) r:10÷2=5(m)
S=π(R2-r2)=3.14×(25×25-5×5)=3.14×600=1884(m ) 答:略
(2)r:31.4÷6.28=5(米) R:5+1=6(米)
3.14×(6×6)-3.14×(5×5)=3.14×36-3.14×25=34.54(平方米) 答:略
3.略
4.略
【精练反馈】
1.33÷2=16.5(米)
14÷2=7(米)
26.4÷2=13.2(米)
14.4÷2=7.2(米)
3.14×(16.5×16.5-7×7)=701.005(平方米)
3.14×(13.2×13.2-7.2×7.2)=384.336(平方米)
701.005-384.336=316.669(平方米)
答:略
2.大圆半径:2+2=4
小圆半径:4÷2=2
3.14×(4×4-2×2)=3.14×12=37.86
37.86÷2=18.84
答:略
3.(1)大圆半径:12÷2=6(cm)
小圆半径:8÷2=4(cm)3.14×(6+4)=3.14×10=31.4(cm)
12-8=4(cm) 31.4+4=35.4(cm)
答:略
(2)3.14×(12×12-8×8)=3.14×80=251.2(m )答:略
【课堂小结】略
【拓展延伸】
(1)略
(2)3.14×10×2=62.8(cm)
(3)3.14×(10÷2)×(10÷2)=78.5(cm ) 78.5×2=157(cm )
10×10=100(cm )157-100=57(cm )答:略
【易错收集】略
5 / 6
同课章节目录
