1.4 有理数的加减(1).ppt 课件(共29张PPT)
文档属性
| 名称 | 1.4 有理数的加减(1).ppt 课件(共29张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 950.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-23 15:25:26 | ||
图片预览








文档简介
(共29张PPT)
沪科版 七年级上册
1.4 有理数的加减(1)
有理数的加法
教学目标
使学生掌握有理数加法法则,并能运用法则进行计算;
在有理数加法法则的教学过程中,注意培养学生的观察、比较、归纳及运算能力.
教学重点:
理解有理数加法的意义,掌握有理数加法法则并能应用其法则正确进行有理数的加法运算.
教学难点:异号两数如何进行加法运算.
我们已经学过两个加数都是正数或
一个加数是正数另一个加数是0的加法
(+5)+(+3)=8
例如:
5 + 0 = 5
当两个加数中有负数时,加法如何进行?
导入新课
-2 -1 0 1 2 3 4 5 6 7 8
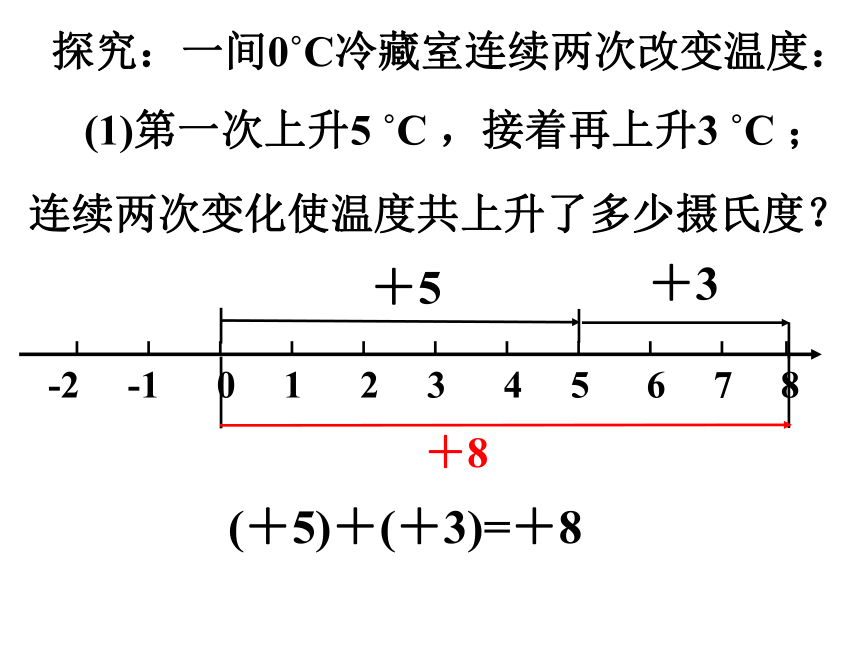
(1)第一次上升5 C ,接着再上升3 C ;
+8
探究:一间0 C冷藏室连续两次改变温度:
(+5)+(+3)=+8
连续两次变化使温度共上升了多少摄氏度?
+5
+3
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2
(2)第一次下降5 C ,接着再下降3 C
-3
-5
-8
探究:一间0 C冷藏室连续两次改变温度:
(-5)+(-3)=-8
连续两次变化使温度共上升了多少摄氏度?
(+5)+(+3)=+8
(-5)+(-3)=-8
结论:同号两数相加,取与加数相同的符号,
并把绝对值相加.
从上面问题中,你能得出同号两数相加的方法吗?
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2
(3)第一次下降5 C ,接着再上升3 C ;
+3
(-5) + (+3)= ?
-5
-2
-2
探究:一间0 C冷藏室连续两次改变温度:
连续两次变化使温度共上升了多少摄氏度?
(-3)+(+5)=?
-6 -5 -4 -3 -2 -1 0 1 2 3 4
(4)第一次下降3 C ,接着再上升5 C ;
+5
-3
+2
探究:一间0 C冷藏室连续两次改变温度:
连续两次变化使温度共上升了多少摄氏度?
+2
(-3)+(+5)=+2
(-5) + (+3)= -2
结论:绝对值不相等的异号两数相加,
取绝对值较大的加数的符号,
并用较大的绝对值减去较小的绝对值.
从上面问题中,你能得出异号两数相加的方法吗?
如果先上升5 C ,接着又下降5 C ,
那么温度又是多少?
+5
-5
结论:互为相反数的两个数相加得零.
(+5)+(-5)=0
-2 -1 0 1 2 3 4 5 6 7 8
探究:一间0 C冷藏室连续两次改变温度:
如果先下降5 C ,接着又上升0 C ,
那么温度又是多少?
-5
(-5)+0=-5
结论:一个数同零相加,仍得这个数.
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2
探究:一间0 C冷藏室连续两次改变温度:
1.同号两数相加,取相同的符号,并把绝对值相加.
2.绝对值不相等的异号两数相加,取绝对值较大
的加数的符号,并用较大的绝对值减去较小的
绝对值.互为相反数的两个数相加得0.
3.一个数同0相加,仍得这个数.
有 理 数 加 法 法 则
例1 计算:
(1) (+7)+(+6); (2)(-5)+(-9);
(3) (- )+ ; (4)(-10.5)+(+21.5).
13;
=
=
(7+6)
+
(1) (+7)+(+6)
1
2
1
3
解析(1)
因为+7和+6都是正数,它们是同号两数相加,
所以结果取它们相同的符号“+”号,
再把绝对值相加.
例1 计算:
(1) (+7)+(+6); (2)(-5)+(-9);
(3) (- )+ ; (4)(-10.5)+(+21.5).
-14;
=
=
(5+9)
-
(2) (-5)+(-9)
1
2
1
3
解析(2)
因为-5和-9都是负数,它们是同号两数相加,
所以结果取它们相同的符号“-”号,
再把绝对值相加.
例1 计算:
(3) (- )+ ; (4)(-10.5)+(+21.5)
=- ;
=
=
( - )
-
1
2
1
3
解析(3)
所以结果要取它们中绝对值较大的符号,
再用较大绝对值减去较小的绝对值.
所以结果取“-”号,
因为- 和 ,一个是负数,一个是正数,
它们是异号两数相加,
1
2
1
3
1
2
因为
|- | >
| |,
1
3
(3) (- )+
1
2
1
3
1
2
1
3
( - )
-
3
6
2
6
1
6
例1 计算:
(3) (- )+ ; (4)(-10.5)+(+21.5)
=11.
=
( 21.5 -10.5 )
+
1
2
1
3
解析(4)
所以结果要取它们中绝对值较大的符号,
再用较大绝对值减去较小的绝对值.
所以结果取“+”号,
因为-10.5和+21.5,一个是负数,一个是正数,
它们是异号两数相加,
因为
|+21.5| >
|-10.5 |,
(4)(-10.5)+(+21.5)
例1 计算:
(1) (+7)+(+6); (2)(-5)+(-9);
(3) (- )+ ; (4)(-10.5)+(+21.5).
解:
-
13;
=
=
(7+6)
-
+
(1) (+7)+(+6)
(2)(-5)+(-9)=
(5+9)
=
14;
(4)(-10.5)+(+21.5)
(21.5 -10.5)
=
+
=
11.
(3) (- )+ =
-
1
2
1
3
1
2
1
3
( - )
=
1
2
1
3
-
1
6
例2 计算:
(1) (-7.5)+(+7.5); (2)(-3.5)+0.
解:
(1) (-7.5)+(+7.5)
=0
(2) (-3.5)+0
=-3.5.
(一个数同0相加,仍得这个数)
(互为相反数相加得0)
怎样进行有理数的加法,你能说说你是按什么思路的吗?
第一步,观察是同号还是异号相加 ;
第二步,确定和的符号;
第三步,进行绝对值的加减运算.
一观察,二确定,三求和.
练习1:口算
(+1)+(+ 2)= ; (-2)+(-7) = ;
(+13)+(-6)= ; (-4)+0= .
练习巩固
3
-9
7
-4
练习2:计算
(1)(+3.5)+(+4.5); (2) (- )+(- ) ;
(3) (- )+(+ ); (4)(+ )+(- ).
7
5
3
5
5
4
13
4
17
16
23
8
解:
(1)(+3.5) +(+4.5)=
+
(3.5+4.5)
=8
-
( + )
7
5
3
5
(2) (- )+(- )=
7
5
3
5
=
10
5
=2
(3) (- )+(+ )=
17
16
5
4
+
( - )
17
16
5
4
=
3
16
(4) (+ )+(- )=
23
8
13
4
( - )
-
23
8
13
4
=-
3
8
例 若某天早晨的气温是- 14℃,中午的气 温比早晨的气温高5℃,则这天中午的气温是多少
解:因为中午的气温比早晨的气温高5℃,
所以
= -(14 -5)
= - 9(℃)
答:中午的气温是- 9℃.
- 14 + 5
例题解析 有理数加法的应用
小明从家里出发骑车到一个公园去玩,当意识到骑过头的时候,他已经骑了4.5km.于是他又往相反的方向骑了1.2km才到达目的地.
(1)小明家离公园有多远
(2)求小明骑车行驶的路程.
解:(1)
4.5+( -1.2)
= +(4.5 -1.2)
= 3.3
(km)
小明家离公园有3.3km.
(2)
4.5+1.2
= 5.7
(km)
小明骑车行驶的路程为5.7km.
学以致用
(1)本节课学习了什么内容?
(2)有理数加法计算的一般步骤是什么?
(3)有理数加法与算术数加法的最大区别是什么?
课堂小结:
. 1.计算(- 5)+3的结果是( ).
A. - 2 B.2 C. - 8 D.8
2.下列各式计算正确的是( ).
A.(-3)+(-4)=-7 B.4+(-9)=9
C.(- 7)+9=-2 D.(-3)+3=6
巩固提高
A
A
3.若两个有理数的和为负数,则这两个数( ).
A.一定都是负数
B.一个为零,另一个为负数
C.一个为正数,一个为负数
D.至少有一个为负数
4.与- 5的和为0的数是( ).
A.5 B. - 5 C. D. -
1
5
1
5
D
A
今天作业
课本P26第1题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
沪科版 七年级上册
1.4 有理数的加减(1)
有理数的加法
教学目标
使学生掌握有理数加法法则,并能运用法则进行计算;
在有理数加法法则的教学过程中,注意培养学生的观察、比较、归纳及运算能力.
教学重点:
理解有理数加法的意义,掌握有理数加法法则并能应用其法则正确进行有理数的加法运算.
教学难点:异号两数如何进行加法运算.
我们已经学过两个加数都是正数或
一个加数是正数另一个加数是0的加法
(+5)+(+3)=8
例如:
5 + 0 = 5
当两个加数中有负数时,加法如何进行?
导入新课
-2 -1 0 1 2 3 4 5 6 7 8
(1)第一次上升5 C ,接着再上升3 C ;
+8
探究:一间0 C冷藏室连续两次改变温度:
(+5)+(+3)=+8
连续两次变化使温度共上升了多少摄氏度?
+5
+3
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2
(2)第一次下降5 C ,接着再下降3 C
-3
-5
-8
探究:一间0 C冷藏室连续两次改变温度:
(-5)+(-3)=-8
连续两次变化使温度共上升了多少摄氏度?
(+5)+(+3)=+8
(-5)+(-3)=-8
结论:同号两数相加,取与加数相同的符号,
并把绝对值相加.
从上面问题中,你能得出同号两数相加的方法吗?
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2
(3)第一次下降5 C ,接着再上升3 C ;
+3
(-5) + (+3)= ?
-5
-2
-2
探究:一间0 C冷藏室连续两次改变温度:
连续两次变化使温度共上升了多少摄氏度?
(-3)+(+5)=?
-6 -5 -4 -3 -2 -1 0 1 2 3 4
(4)第一次下降3 C ,接着再上升5 C ;
+5
-3
+2
探究:一间0 C冷藏室连续两次改变温度:
连续两次变化使温度共上升了多少摄氏度?
+2
(-3)+(+5)=+2
(-5) + (+3)= -2
结论:绝对值不相等的异号两数相加,
取绝对值较大的加数的符号,
并用较大的绝对值减去较小的绝对值.
从上面问题中,你能得出异号两数相加的方法吗?
如果先上升5 C ,接着又下降5 C ,
那么温度又是多少?
+5
-5
结论:互为相反数的两个数相加得零.
(+5)+(-5)=0
-2 -1 0 1 2 3 4 5 6 7 8
探究:一间0 C冷藏室连续两次改变温度:
如果先下降5 C ,接着又上升0 C ,
那么温度又是多少?
-5
(-5)+0=-5
结论:一个数同零相加,仍得这个数.
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2
探究:一间0 C冷藏室连续两次改变温度:
1.同号两数相加,取相同的符号,并把绝对值相加.
2.绝对值不相等的异号两数相加,取绝对值较大
的加数的符号,并用较大的绝对值减去较小的
绝对值.互为相反数的两个数相加得0.
3.一个数同0相加,仍得这个数.
有 理 数 加 法 法 则
例1 计算:
(1) (+7)+(+6); (2)(-5)+(-9);
(3) (- )+ ; (4)(-10.5)+(+21.5).
13;
=
=
(7+6)
+
(1) (+7)+(+6)
1
2
1
3
解析(1)
因为+7和+6都是正数,它们是同号两数相加,
所以结果取它们相同的符号“+”号,
再把绝对值相加.
例1 计算:
(1) (+7)+(+6); (2)(-5)+(-9);
(3) (- )+ ; (4)(-10.5)+(+21.5).
-14;
=
=
(5+9)
-
(2) (-5)+(-9)
1
2
1
3
解析(2)
因为-5和-9都是负数,它们是同号两数相加,
所以结果取它们相同的符号“-”号,
再把绝对值相加.
例1 计算:
(3) (- )+ ; (4)(-10.5)+(+21.5)
=- ;
=
=
( - )
-
1
2
1
3
解析(3)
所以结果要取它们中绝对值较大的符号,
再用较大绝对值减去较小的绝对值.
所以结果取“-”号,
因为- 和 ,一个是负数,一个是正数,
它们是异号两数相加,
1
2
1
3
1
2
因为
|- | >
| |,
1
3
(3) (- )+
1
2
1
3
1
2
1
3
( - )
-
3
6
2
6
1
6
例1 计算:
(3) (- )+ ; (4)(-10.5)+(+21.5)
=11.
=
( 21.5 -10.5 )
+
1
2
1
3
解析(4)
所以结果要取它们中绝对值较大的符号,
再用较大绝对值减去较小的绝对值.
所以结果取“+”号,
因为-10.5和+21.5,一个是负数,一个是正数,
它们是异号两数相加,
因为
|+21.5| >
|-10.5 |,
(4)(-10.5)+(+21.5)
例1 计算:
(1) (+7)+(+6); (2)(-5)+(-9);
(3) (- )+ ; (4)(-10.5)+(+21.5).
解:
-
13;
=
=
(7+6)
-
+
(1) (+7)+(+6)
(2)(-5)+(-9)=
(5+9)
=
14;
(4)(-10.5)+(+21.5)
(21.5 -10.5)
=
+
=
11.
(3) (- )+ =
-
1
2
1
3
1
2
1
3
( - )
=
1
2
1
3
-
1
6
例2 计算:
(1) (-7.5)+(+7.5); (2)(-3.5)+0.
解:
(1) (-7.5)+(+7.5)
=0
(2) (-3.5)+0
=-3.5.
(一个数同0相加,仍得这个数)
(互为相反数相加得0)
怎样进行有理数的加法,你能说说你是按什么思路的吗?
第一步,观察是同号还是异号相加 ;
第二步,确定和的符号;
第三步,进行绝对值的加减运算.
一观察,二确定,三求和.
练习1:口算
(+1)+(+ 2)= ; (-2)+(-7) = ;
(+13)+(-6)= ; (-4)+0= .
练习巩固
3
-9
7
-4
练习2:计算
(1)(+3.5)+(+4.5); (2) (- )+(- ) ;
(3) (- )+(+ ); (4)(+ )+(- ).
7
5
3
5
5
4
13
4
17
16
23
8
解:
(1)(+3.5) +(+4.5)=
+
(3.5+4.5)
=8
-
( + )
7
5
3
5
(2) (- )+(- )=
7
5
3
5
=
10
5
=2
(3) (- )+(+ )=
17
16
5
4
+
( - )
17
16
5
4
=
3
16
(4) (+ )+(- )=
23
8
13
4
( - )
-
23
8
13
4
=-
3
8
例 若某天早晨的气温是- 14℃,中午的气 温比早晨的气温高5℃,则这天中午的气温是多少
解:因为中午的气温比早晨的气温高5℃,
所以
= -(14 -5)
= - 9(℃)
答:中午的气温是- 9℃.
- 14 + 5
例题解析 有理数加法的应用
小明从家里出发骑车到一个公园去玩,当意识到骑过头的时候,他已经骑了4.5km.于是他又往相反的方向骑了1.2km才到达目的地.
(1)小明家离公园有多远
(2)求小明骑车行驶的路程.
解:(1)
4.5+( -1.2)
= +(4.5 -1.2)
= 3.3
(km)
小明家离公园有3.3km.
(2)
4.5+1.2
= 5.7
(km)
小明骑车行驶的路程为5.7km.
学以致用
(1)本节课学习了什么内容?
(2)有理数加法计算的一般步骤是什么?
(3)有理数加法与算术数加法的最大区别是什么?
课堂小结:
. 1.计算(- 5)+3的结果是( ).
A. - 2 B.2 C. - 8 D.8
2.下列各式计算正确的是( ).
A.(-3)+(-4)=-7 B.4+(-9)=9
C.(- 7)+9=-2 D.(-3)+3=6
巩固提高
A
A
3.若两个有理数的和为负数,则这两个数( ).
A.一定都是负数
B.一个为零,另一个为负数
C.一个为正数,一个为负数
D.至少有一个为负数
4.与- 5的和为0的数是( ).
A.5 B. - 5 C. D. -
1
5
1
5
D
A
今天作业
课本P26第1题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
