1.5 有理数的乘除(1) 课件(共27张PPT)
文档属性
| 名称 | 1.5 有理数的乘除(1) 课件(共27张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 929.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-23 15:22:46 | ||
图片预览





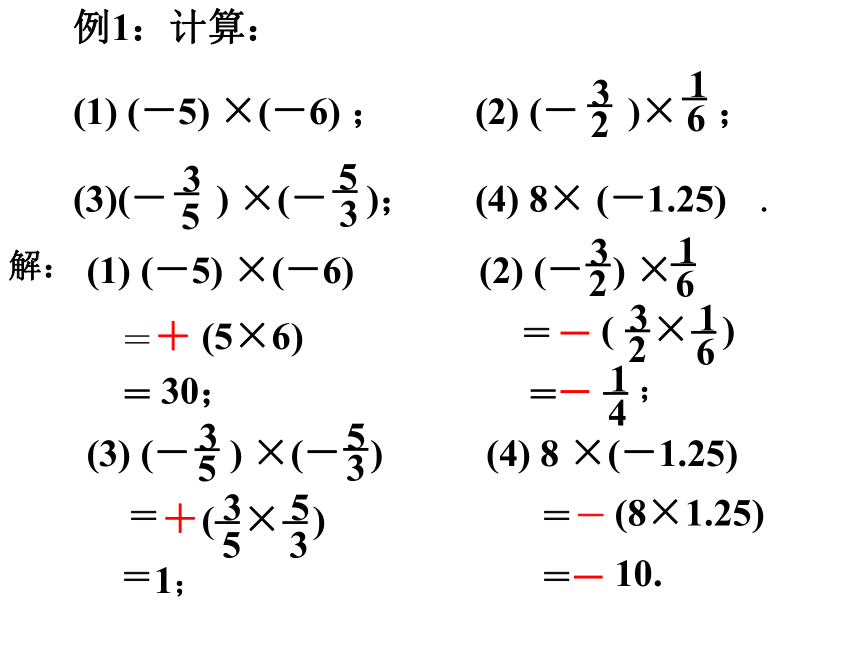

文档简介
(共27张PPT)
1.5有理数的乘除(1)
有理数的乘法
沪科版 七年级上册
1.5有理数的乘除(1)
有理数的乘法
教学目标
理解有理数的乘法的意义,掌握有理数乘法法则,能熟练运用有理数乘法法则进行乘法运算.算.
教学重点
使学生理解有理数乘法的意义,掌握有理数
乘法法则,并能准确地进行有理数的乘法运算.
教学难点:
有理数乘法法则的理解.
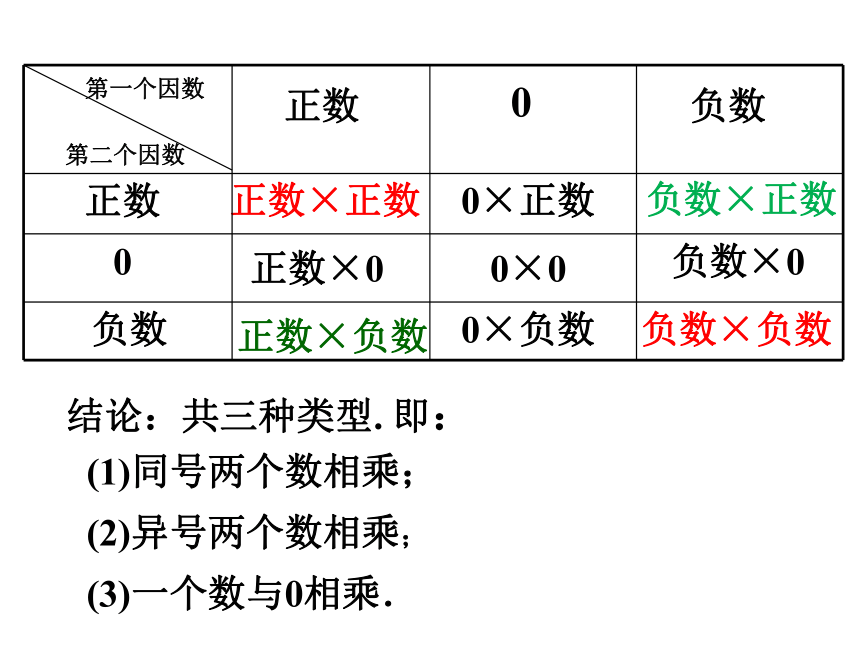
在小学,我们学过正数及0的乘法运算.学过的乘法类型是正数与正数相乘、正数与0相乘.引入负数后,乘法的类型还有哪几种呢?
正数×正数
0×正数
负数×正数
0×0
负数×0
0×负数
负数×负数
第一个因数
第二个因数
正数
0
负数
正数
0
负数
结论:共三种类型. 即:
(1)同号两个数相乘;
(2)异号两个数相乘;
(3)一个数与0相乘.
正数×0
正数×负数
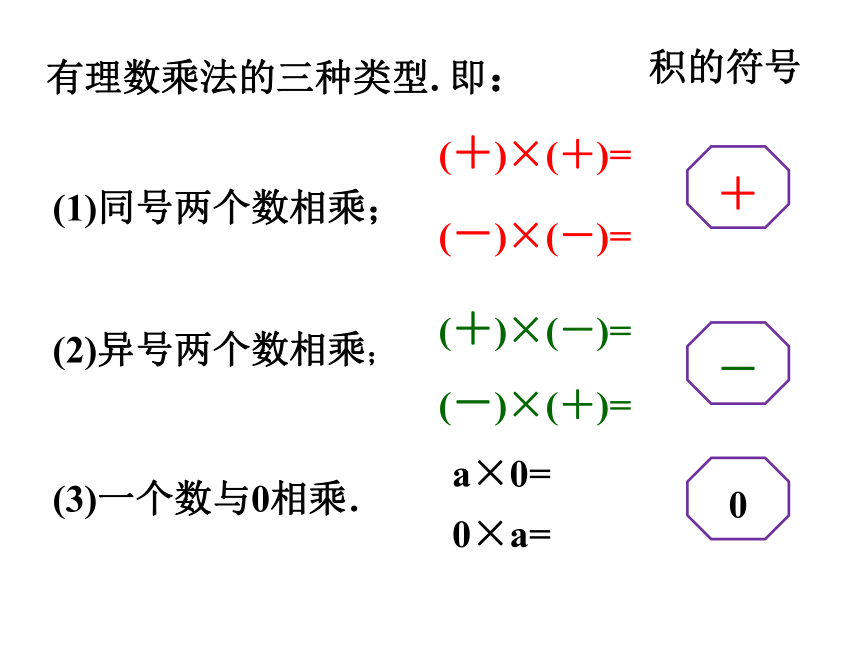
有理数乘法的三种类型. 即:
(1)同号两个数相乘;
(2)异号两个数相乘;
(3)一个数与0相乘.
(+)×(+)=
(-)×(-)=
+
(+)×(-)=
(-)×(+)=
-
a×0=
0×a=
0
积的符号
有理数乘法法则:
两数相乘,同号得正,异号得负,
并把绝对值相乘.
任何数同0相乘,都得0.
例1:计算:
(1) (-5) ×(-6) ; (2) (- )× ;
(3)(- ) ×(- ); (4) 8× (-1.25) .
解:
+
=
10.
30;
=
=
—
( × )
— ;
=
=
( × )
=
1;
=
=
-
(8×1.25)
(5×6)
+
3
2
1
6
3
5
5
3
(1) (-5) ×(-6)
(2) (- ) ×
3
2
1
6
3
2
1
6
1
4
—
(4) 8 ×(-1.25)
(3) (- ) ×(- )
3
5
5
3
3
5
5
3
两个有理数相乘,先确定积的_____,
再确定积的______.
有理数乘法的步骤:
符号
绝对值
-
+
-
+
你能很快的确定下列各式的符号吗
(-2)× 4
3 × 5
(-4) × (-6)
9 × (-1)
(-5) × 0
0
1.填写下表:
因数 因数 积的符号 积的绝对值 积
+8 -6
-10 +8
-9 -4
20 8
-
-
+
+
48
80
36
-48
-80
36
160
160
2.计算:
(1) (-4.6) ×(+3) ; (2) ×(- ) ;
(3)(- ) ×(- ); (4) (- )× (- );
(5) (+4.6) ×(-3) ; (6) (- )×(-12 ) ;
(7)(-3.8 )×0; (8) 100× (-0.01 ).
5
8
2
5
3
4
3
4
8
9
2
3
3
2
2.计算:
(1) (-4.6)×(+3) (2) ×(- )
(3)(- ) ×(- ) (4) (- )× (- )
2
5
3
4
3
4
8
9
2
3
3
2
=
-
(4.6×3)
=
-
( × )
=
-
13.8
=
-
=
+
( × )
=
3
4
8
9
2
3
2
5
3
4
3
10
=
+
( × )
=
2
3
3
2
1
2.计算:
(5) (+8.5)×(-2) ; (6) (- )×(-12 ) ;
(7)(-3.8 )×0; (8) 100× (-0.01 ).
5
8
=
-
(8.5×2)
=
-
17
=
+
( ×12)
=
=0
=
-
(100×0.01)
=
-
1
5
8
15
2
计算:
观察两式有什么特点?
乘积是1.
思考:数
的倒数是什么?
(1)
(2)
数a(a≠0)的倒数是 .
在有理数范围内,如果两个数的乘积为1,我们称这两个数互为倒数.
(- )× (-2)=
1
2
(- )× (- )=
3
5
5
3
1
a
1
1
(1)一个数的倒数等于它本身,那么这个
数是_______.
写出下列各数的倒数.
1或-1
-5
5
-1
1
原数
解:
1
-1
3
-3
倒数
观察并讨论:
(2) 0有没有倒数?
1
3
-
1
3
2
3
-
2
3
1
5
-
1
5
3
2
-
3
2
计算:
(1)(-4)×5×(-0.25)
(2)(- )×(-16)×(+0.5)×(-4)
(3)(+2)×(-8.5)×(-100)×0×(+90)
(4×5×0.25)
= 5
( ×16×0.5×4)
=-12
0
(1)先确定积的符号;
=
+
=
-
=
3
8
3
8
(2)再求绝对值之积.
由上面的式子,我得出下面的规律:
几个数相乘,有一个因数为0,积为0.
几个不为0的数相乘,积的符号由负因数的个数决定.当负因数有奇数个时,积的符号为负;当负因数有偶数个时,积的符号为正.
1.(口答) 确定下列积的符号:
(1)(-5)×4×(-1)×3
(2)(-4)×6×(-7)×(-3)
(3)(-1)×(-1)×(-1)
(4)(-2)×(-2)×(-2)×(-2)
+
-
-
+
2.计算:
(1)(-7)×(-9) ×(-8)
(2)(-8.46)×2.5×(-4)
=
-
(7×9×8)
= - 504
=
+
(8.46×2.5×4)
=84.6
3.计算:
(1)-8×(+12)×(-7)×13
(2)(-100)×72×(-50)×0×(-2)
=0
=
+
(8×12×7×13)
=8736
1.本节课你学到了什么?
2.本节课你有何收获?
3.你还有什么疑问?
课堂小结:
1.下列算式的积为正数的是( ).
A.(-2) ×x(+ ) B.(- 6) ×(- 2)
C.0×x(- 1) D.(+5) ×(- 2)
1
2
2.给出下列计算:
①3×(-4)=-12, ②(-4)×(-6)=24,
③(-5)×(-1)= -5, ④(-2)×12=24.
其中正确的个数为( ).
A.4 B.3 C.2 D.1
巩固提高
B
C
4.下列说法错误的是( ).
A.一个数同1相乘,仍得这个数
B.一个数同-1相乘,得原数的相反数
C.互为相反数的两数之积为1
D.一个数同0相乘,得0
3.若三个有理数相乘的积为0,则这三个
有理数( ).
A.至少有一个数为0 B.都是0
C.只有一个数为0 D.不可能有两个以上数为0
A
C
今天作业
课本P37第1、2题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
1.5有理数的乘除(1)
有理数的乘法
沪科版 七年级上册
1.5有理数的乘除(1)
有理数的乘法
教学目标
理解有理数的乘法的意义,掌握有理数乘法法则,能熟练运用有理数乘法法则进行乘法运算.算.
教学重点
使学生理解有理数乘法的意义,掌握有理数
乘法法则,并能准确地进行有理数的乘法运算.
教学难点:
有理数乘法法则的理解.
在小学,我们学过正数及0的乘法运算.学过的乘法类型是正数与正数相乘、正数与0相乘.引入负数后,乘法的类型还有哪几种呢?
正数×正数
0×正数
负数×正数
0×0
负数×0
0×负数
负数×负数
第一个因数
第二个因数
正数
0
负数
正数
0
负数
结论:共三种类型. 即:
(1)同号两个数相乘;
(2)异号两个数相乘;
(3)一个数与0相乘.
正数×0
正数×负数
有理数乘法的三种类型. 即:
(1)同号两个数相乘;
(2)异号两个数相乘;
(3)一个数与0相乘.
(+)×(+)=
(-)×(-)=
+
(+)×(-)=
(-)×(+)=
-
a×0=
0×a=
0
积的符号
有理数乘法法则:
两数相乘,同号得正,异号得负,
并把绝对值相乘.
任何数同0相乘,都得0.
例1:计算:
(1) (-5) ×(-6) ; (2) (- )× ;
(3)(- ) ×(- ); (4) 8× (-1.25) .
解:
+
=
10.
30;
=
=
—
( × )
— ;
=
=
( × )
=
1;
=
=
-
(8×1.25)
(5×6)
+
3
2
1
6
3
5
5
3
(1) (-5) ×(-6)
(2) (- ) ×
3
2
1
6
3
2
1
6
1
4
—
(4) 8 ×(-1.25)
(3) (- ) ×(- )
3
5
5
3
3
5
5
3
两个有理数相乘,先确定积的_____,
再确定积的______.
有理数乘法的步骤:
符号
绝对值
-
+
-
+
你能很快的确定下列各式的符号吗
(-2)× 4
3 × 5
(-4) × (-6)
9 × (-1)
(-5) × 0
0
1.填写下表:
因数 因数 积的符号 积的绝对值 积
+8 -6
-10 +8
-9 -4
20 8
-
-
+
+
48
80
36
-48
-80
36
160
160
2.计算:
(1) (-4.6) ×(+3) ; (2) ×(- ) ;
(3)(- ) ×(- ); (4) (- )× (- );
(5) (+4.6) ×(-3) ; (6) (- )×(-12 ) ;
(7)(-3.8 )×0; (8) 100× (-0.01 ).
5
8
2
5
3
4
3
4
8
9
2
3
3
2
2.计算:
(1) (-4.6)×(+3) (2) ×(- )
(3)(- ) ×(- ) (4) (- )× (- )
2
5
3
4
3
4
8
9
2
3
3
2
=
-
(4.6×3)
=
-
( × )
=
-
13.8
=
-
=
+
( × )
=
3
4
8
9
2
3
2
5
3
4
3
10
=
+
( × )
=
2
3
3
2
1
2.计算:
(5) (+8.5)×(-2) ; (6) (- )×(-12 ) ;
(7)(-3.8 )×0; (8) 100× (-0.01 ).
5
8
=
-
(8.5×2)
=
-
17
=
+
( ×12)
=
=0
=
-
(100×0.01)
=
-
1
5
8
15
2
计算:
观察两式有什么特点?
乘积是1.
思考:数
的倒数是什么?
(1)
(2)
数a(a≠0)的倒数是 .
在有理数范围内,如果两个数的乘积为1,我们称这两个数互为倒数.
(- )× (-2)=
1
2
(- )× (- )=
3
5
5
3
1
a
1
1
(1)一个数的倒数等于它本身,那么这个
数是_______.
写出下列各数的倒数.
1或-1
-5
5
-1
1
原数
解:
1
-1
3
-3
倒数
观察并讨论:
(2) 0有没有倒数?
1
3
-
1
3
2
3
-
2
3
1
5
-
1
5
3
2
-
3
2
计算:
(1)(-4)×5×(-0.25)
(2)(- )×(-16)×(+0.5)×(-4)
(3)(+2)×(-8.5)×(-100)×0×(+90)
(4×5×0.25)
= 5
( ×16×0.5×4)
=-12
0
(1)先确定积的符号;
=
+
=
-
=
3
8
3
8
(2)再求绝对值之积.
由上面的式子,我得出下面的规律:
几个数相乘,有一个因数为0,积为0.
几个不为0的数相乘,积的符号由负因数的个数决定.当负因数有奇数个时,积的符号为负;当负因数有偶数个时,积的符号为正.
1.(口答) 确定下列积的符号:
(1)(-5)×4×(-1)×3
(2)(-4)×6×(-7)×(-3)
(3)(-1)×(-1)×(-1)
(4)(-2)×(-2)×(-2)×(-2)
+
-
-
+
2.计算:
(1)(-7)×(-9) ×(-8)
(2)(-8.46)×2.5×(-4)
=
-
(7×9×8)
= - 504
=
+
(8.46×2.5×4)
=84.6
3.计算:
(1)-8×(+12)×(-7)×13
(2)(-100)×72×(-50)×0×(-2)
=0
=
+
(8×12×7×13)
=8736
1.本节课你学到了什么?
2.本节课你有何收获?
3.你还有什么疑问?
课堂小结:
1.下列算式的积为正数的是( ).
A.(-2) ×x(+ ) B.(- 6) ×(- 2)
C.0×x(- 1) D.(+5) ×(- 2)
1
2
2.给出下列计算:
①3×(-4)=-12, ②(-4)×(-6)=24,
③(-5)×(-1)= -5, ④(-2)×12=24.
其中正确的个数为( ).
A.4 B.3 C.2 D.1
巩固提高
B
C
4.下列说法错误的是( ).
A.一个数同1相乘,仍得这个数
B.一个数同-1相乘,得原数的相反数
C.互为相反数的两数之积为1
D.一个数同0相乘,得0
3.若三个有理数相乘的积为0,则这三个
有理数( ).
A.至少有一个数为0 B.都是0
C.只有一个数为0 D.不可能有两个以上数为0
A
C
今天作业
课本P37第1、2题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
