1.5 有理数的乘除(3) 课件(共26张PPT)
文档属性
| 名称 | 1.5 有理数的乘除(3) 课件(共26张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 968.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-23 15:20:27 | ||
图片预览






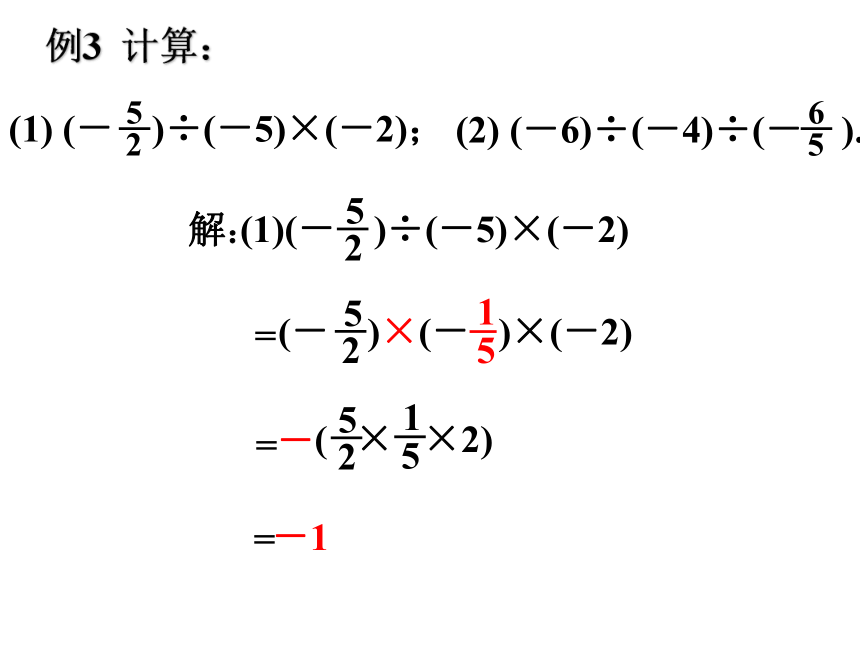
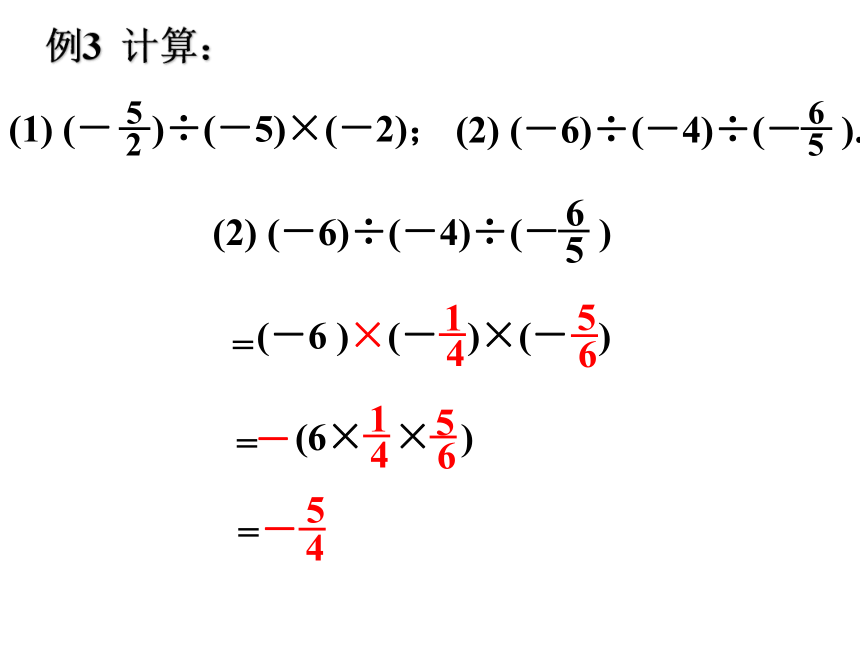
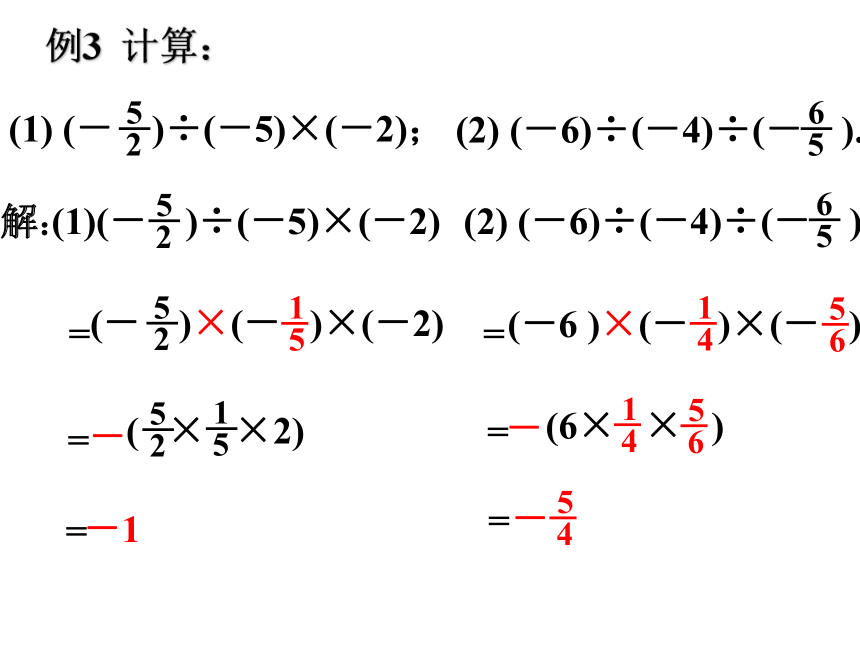
文档简介
(共26张PPT)
沪科版 七年级上册
1.5有理数的乘除(3)
教学目标
1.进一步掌握有理数的运算法则和运算律.
2.使学生能够熟练地按有理数运算顺序进行
混合运算.
3.注意培养学生的运算能力.
教学重点:有理数的混合运算.
教学难点:准确地掌握有理数的运算顺序和运算中的符号问题.
有理数乘法法则:
两数相乘,同号得正,异号得负,
并把绝对值相乘.
任何数同0相乘,都得0.
几个数相乘,有一个因数为0,积为0.
几个不为0的数相乘,积的符号由负因数的个数决定.当负因数有奇数个时,积的符号为负;当负因数有偶数个时,积的符号为正.
两个有理数相除, 同号得正, 异号得负,并把绝对值相除;
0除以任何非0数都得0.
除法法则:
除以一个不等于0的数,等于乘这个的数的倒数.
在有理数范围内,如果两个数的乘积为1,我们称这两个数互为倒数.
(-18) ÷6
(-63) ÷(-7)
1 ÷(-9)
0÷(-8)
(5) (-6.5) ÷0.13 =
(6) (- )÷(- )
6
5
2
5
-50
=0
=-
1
9
=9
=-3
=3
口算
例3 计算:
(1) (- )÷(-5)×(-2);
(2) (-6)÷(-4)÷(- ).
6
5
5
2
解:
(1)(- )÷(-5)×(-2)
5
2
=
(- )×(- )×(-2)
5
2
=
-
1
5
( × ×2)
1
5
5
2
=
-1
例3 计算:
(1) (- )÷(-5)×(-2);
(2) (-6)÷(-4)÷(- ).
6
5
5
2
(2) (-6)÷(-4)÷(- )
6
5
=
(-6 )×(- )×(- )
1
4
5
6
=
-
(6× × )
1
4
5
6
=
-
5
4
例3 计算:
(1) (- )÷(-5)×(-2);
(2) (-6)÷(-4)÷(- ).
6
5
5
2
解:
(1)(- )÷(-5)×(-2)
5
2
=
(- )×(- )×(-2)
5
2
=
-
1
5
( × ×2)
1
5
5
2
=
-1
(2) (-6)÷(-4)÷(- )
6
5
=
(-6 )×(- )×(- )
1
4
5
6
=
-
(6× × )
1
4
5
6
=
-
5
4
例4 计算:
(1) + ÷(- ) - ×(- );
3
4
1
5
4
5
2
5
5
4
(2) -5+(1-0.2× )÷(-2).
5
3
先算乘除,再算加减,同级运算从左往右依次计算,如有括号,先算括号内的.
混合运算的顺序
例4 计算:
(1) + ÷(- ) - ×(- );
3
4
1
5
4
5
2
5
5
4
(2) -5+(1-0.2× )÷(-2).
5
3
解:
(1) + ÷(- )- ×(- )
3
4
1
5
4
5
2
5
5
4
=
+ ×(- )- ×(- )
3
4
1
5
5
4
2
5
5
4
=
+ (- )-(- )
3
4
1
4
1
2
=
+
1
2
1
2
=1
-5+(1- × )×(- )
例4 计算:
(2) -5+(1-0.2× )÷(-2)
5
3
=
-5+(- )
1
5
5
3
1
2
=
-5+(1- )×(- )
1
3
1
2
=
-5+ ×(- )
1
2
2
3
=
1
3
=
16
3
-
乘法运算律:
1.乘法交换律:
2.乘法结合律:
3.分配率:
运用这些规律,有时可以简化计算.
ab=ba
(ab)c=a(bc)
a(b+c)=ab+ac
例5 计算:
(1) ( + - )×(-12);
1
4
1
6
1
2
(2) (-0.1)×(-100)×0.01×(-10).
解:
(1) ( + - )×(-12)
1
4
1
6
1
2
=
×(-12)
-
1
4
1
6
1
2
=
-3
+(-2)
-
(-6)
=
1
+
×(-12)
×(-12)
=
-5
+6
(2) (-0.1)×(-100)×0.01×(-10).
-
=
(0.1×100×0.01×10)
=
(0.1×10)
×(100×0.01)
-
=-1
(1) (- ) ×1.25×(-8);
81
20
1.计算:
=
81
20
×(1.25×8)
=
20
81
×10
=
2
81
(2) -3.5÷(- )×(- )
3
4
1.计算:
7
8
=
- ×(- )×(- )
7
2
8
7
3
4
=
-3
2 计算:
(1) ( - + - )×36;
7
9
5
6
3
4
7
18
=
×36
7
9
×36
-
-
5
6
×36
+
3
4
×36
7
18
=
- + -
28
30
27
14
=
55
-
44
=
11
(2) (- )×(- )×(- )× .
2
9
9
2
31
15
5
31
=
-
( × )
× ( × )
5
31
31
15
9
2
2
9
=
-
1
3
1.下列变形不正确的是( ).
A.5×(-6)= -(5×6)= -30
B. -9×5÷(- 4)×0=0
C.(- + )×(-4)=(-4)×(- )+ ×4=2
D.(-25)×(-16)÷(-4)= -(25×16× )=-100
2.计算(- 7)×(- 6)×0÷(- 42)的结果是 .
1
6
1
3
1
6
1
3
1
4
C
0
课堂小结:
3.对( + + )×(-24)进行简便计算.应该
运用( ).
A.加法交换律 B.分配律
C.乘法交换律 D.乘法结合律
4.计算(-1)÷5×(- )的结果是( ).
A. -1 B.1 C. D.25
1
3
1
4
1
2
1
5
25
1
B
C
5.下列各式计算正确的是( ).
A. - 5÷( -1)= -20
B. - 2÷(- 8)×(- )=-2
C. - ×(-2)÷(- )=-40
D.(- + +1)÷(- )=-3
1
5
1
8
8
3
15
2
7
8
16
3
16
1
C
今天作业
课本P37习题1.5第3、5题
有一种“二十四点”的游戏,其游戏的规则是这样的:任取四个1至13之间的自然数,将这四个数(每个数用且只用一次)进行加减乘除四则运算,使其结果等于24.
例如对1,2,3,4可作运算:(1+2+3)×4=24.
现有2组有理数① 3,4,6,10;
② 3,5,7,13.
运用上述规则运算,使其结果等于24.
数学花絮
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
沪科版 七年级上册
1.5有理数的乘除(3)
教学目标
1.进一步掌握有理数的运算法则和运算律.
2.使学生能够熟练地按有理数运算顺序进行
混合运算.
3.注意培养学生的运算能力.
教学重点:有理数的混合运算.
教学难点:准确地掌握有理数的运算顺序和运算中的符号问题.
有理数乘法法则:
两数相乘,同号得正,异号得负,
并把绝对值相乘.
任何数同0相乘,都得0.
几个数相乘,有一个因数为0,积为0.
几个不为0的数相乘,积的符号由负因数的个数决定.当负因数有奇数个时,积的符号为负;当负因数有偶数个时,积的符号为正.
两个有理数相除, 同号得正, 异号得负,并把绝对值相除;
0除以任何非0数都得0.
除法法则:
除以一个不等于0的数,等于乘这个的数的倒数.
在有理数范围内,如果两个数的乘积为1,我们称这两个数互为倒数.
(-18) ÷6
(-63) ÷(-7)
1 ÷(-9)
0÷(-8)
(5) (-6.5) ÷0.13 =
(6) (- )÷(- )
6
5
2
5
-50
=0
=-
1
9
=9
=-3
=3
口算
例3 计算:
(1) (- )÷(-5)×(-2);
(2) (-6)÷(-4)÷(- ).
6
5
5
2
解:
(1)(- )÷(-5)×(-2)
5
2
=
(- )×(- )×(-2)
5
2
=
-
1
5
( × ×2)
1
5
5
2
=
-1
例3 计算:
(1) (- )÷(-5)×(-2);
(2) (-6)÷(-4)÷(- ).
6
5
5
2
(2) (-6)÷(-4)÷(- )
6
5
=
(-6 )×(- )×(- )
1
4
5
6
=
-
(6× × )
1
4
5
6
=
-
5
4
例3 计算:
(1) (- )÷(-5)×(-2);
(2) (-6)÷(-4)÷(- ).
6
5
5
2
解:
(1)(- )÷(-5)×(-2)
5
2
=
(- )×(- )×(-2)
5
2
=
-
1
5
( × ×2)
1
5
5
2
=
-1
(2) (-6)÷(-4)÷(- )
6
5
=
(-6 )×(- )×(- )
1
4
5
6
=
-
(6× × )
1
4
5
6
=
-
5
4
例4 计算:
(1) + ÷(- ) - ×(- );
3
4
1
5
4
5
2
5
5
4
(2) -5+(1-0.2× )÷(-2).
5
3
先算乘除,再算加减,同级运算从左往右依次计算,如有括号,先算括号内的.
混合运算的顺序
例4 计算:
(1) + ÷(- ) - ×(- );
3
4
1
5
4
5
2
5
5
4
(2) -5+(1-0.2× )÷(-2).
5
3
解:
(1) + ÷(- )- ×(- )
3
4
1
5
4
5
2
5
5
4
=
+ ×(- )- ×(- )
3
4
1
5
5
4
2
5
5
4
=
+ (- )-(- )
3
4
1
4
1
2
=
+
1
2
1
2
=1
-5+(1- × )×(- )
例4 计算:
(2) -5+(1-0.2× )÷(-2)
5
3
=
-5+(- )
1
5
5
3
1
2
=
-5+(1- )×(- )
1
3
1
2
=
-5+ ×(- )
1
2
2
3
=
1
3
=
16
3
-
乘法运算律:
1.乘法交换律:
2.乘法结合律:
3.分配率:
运用这些规律,有时可以简化计算.
ab=ba
(ab)c=a(bc)
a(b+c)=ab+ac
例5 计算:
(1) ( + - )×(-12);
1
4
1
6
1
2
(2) (-0.1)×(-100)×0.01×(-10).
解:
(1) ( + - )×(-12)
1
4
1
6
1
2
=
×(-12)
-
1
4
1
6
1
2
=
-3
+(-2)
-
(-6)
=
1
+
×(-12)
×(-12)
=
-5
+6
(2) (-0.1)×(-100)×0.01×(-10).
-
=
(0.1×100×0.01×10)
=
(0.1×10)
×(100×0.01)
-
=-1
(1) (- ) ×1.25×(-8);
81
20
1.计算:
=
81
20
×(1.25×8)
=
20
81
×10
=
2
81
(2) -3.5÷(- )×(- )
3
4
1.计算:
7
8
=
- ×(- )×(- )
7
2
8
7
3
4
=
-3
2 计算:
(1) ( - + - )×36;
7
9
5
6
3
4
7
18
=
×36
7
9
×36
-
-
5
6
×36
+
3
4
×36
7
18
=
- + -
28
30
27
14
=
55
-
44
=
11
(2) (- )×(- )×(- )× .
2
9
9
2
31
15
5
31
=
-
( × )
× ( × )
5
31
31
15
9
2
2
9
=
-
1
3
1.下列变形不正确的是( ).
A.5×(-6)= -(5×6)= -30
B. -9×5÷(- 4)×0=0
C.(- + )×(-4)=(-4)×(- )+ ×4=2
D.(-25)×(-16)÷(-4)= -(25×16× )=-100
2.计算(- 7)×(- 6)×0÷(- 42)的结果是 .
1
6
1
3
1
6
1
3
1
4
C
0
课堂小结:
3.对( + + )×(-24)进行简便计算.应该
运用( ).
A.加法交换律 B.分配律
C.乘法交换律 D.乘法结合律
4.计算(-1)÷5×(- )的结果是( ).
A. -1 B.1 C. D.25
1
3
1
4
1
2
1
5
25
1
B
C
5.下列各式计算正确的是( ).
A. - 5÷( -1)= -20
B. - 2÷(- 8)×(- )=-2
C. - ×(-2)÷(- )=-40
D.(- + +1)÷(- )=-3
1
5
1
8
8
3
15
2
7
8
16
3
16
1
C
今天作业
课本P37习题1.5第3、5题
有一种“二十四点”的游戏,其游戏的规则是这样的:任取四个1至13之间的自然数,将这四个数(每个数用且只用一次)进行加减乘除四则运算,使其结果等于24.
例如对1,2,3,4可作运算:(1+2+3)×4=24.
现有2组有理数① 3,4,6,10;
② 3,5,7,13.
运用上述规则运算,使其结果等于24.
数学花絮
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
