12.1 函数(3)课件(共30张PPT)
文档属性
| 名称 | 12.1 函数(3)课件(共30张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-26 17:42:48 | ||
图片预览








文档简介
(共30张PPT)
沪科版 八年级上册
12.1 函数 (3)
学习目标:
1.通过阅读教材了解函数图象法的意义.
2.经历画函数图象的过程,体会数形结合的特点,认识函数图象的意义,掌握函数图象的画法.
学习重难点:认识函数图象的意义,掌握函数
图象的画法.
1. 如何求函数自变量的取值范围?
函数y= 中,自变量x的取值范围是( )
A.x>1 B.x≥1 C.x>-2 D.x≥-2
A
x-1
x+2
在一个函数关系式中,同时有几种代数式,函数自变量的取值范围应是各种代数式中自变量取值范围的公共部分.
复习旧知
1. 如何求函数自变量的取值范围?
函数y= 中,自变量x的取值范围是( )
A.x>1 B.x≥1 C.x>-2 D.x≥-2
A
x-1
x+2
y=
x-1
x+2
x≥1
y=
x-1
x-2
x≥1,
但x≠2
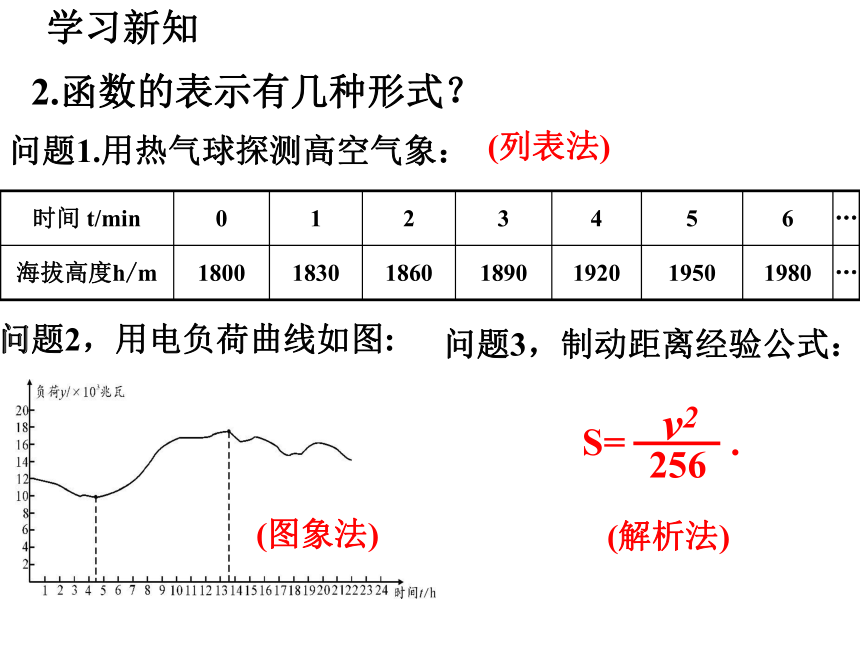
2.函数的表示有几种形式?
问题1.用热气球探测高空气象:
时间 t/min 0 1 2 3 4 5 6 …
海拔高度h/m 1800 1830 1860 1890 1920 1950 1980 …
问题2,用电负荷曲线如图:
问题3,制动距离经验公式:
S= .
v2
256
(列表法)
(解析法)
(图象法)
学习新知
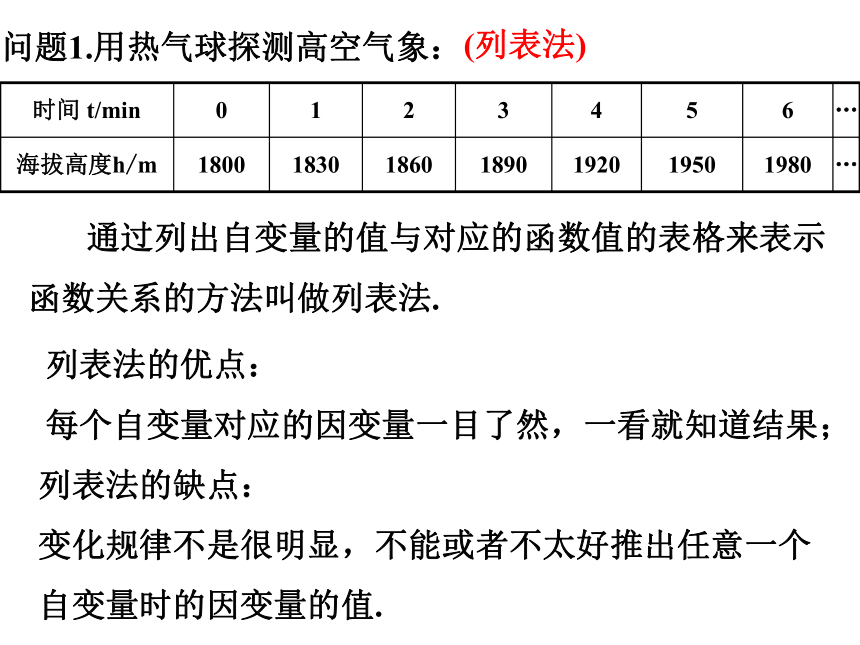
问题1.用热气球探测高空气象:
时间 t/min 0 1 2 3 4 5 6 …
海拔高度h/m 1800 1830 1860 1890 1920 1950 1980 …
(列表法)
列表法的优点:
每个自变量对应的因变量一目了然,一看就知道结果;
列表法的缺点:
变化规律不是很明显,不能或者不太好推出任意一个自变量时的因变量的值.
通过列出自变量的值与对应的函数值的表格来表示函数关系的方法叫做列表法.
问题3,制动距离经验公式:
S= .
v2
256
(解析法)
用关于自变量的数学式子表示函数与自变量之间的关系的方法,叫做解析法.
解析法优点:
自变量与因变量的关系一看就知道,
解析法缺点:
涉及到具体数量还要进行计算.
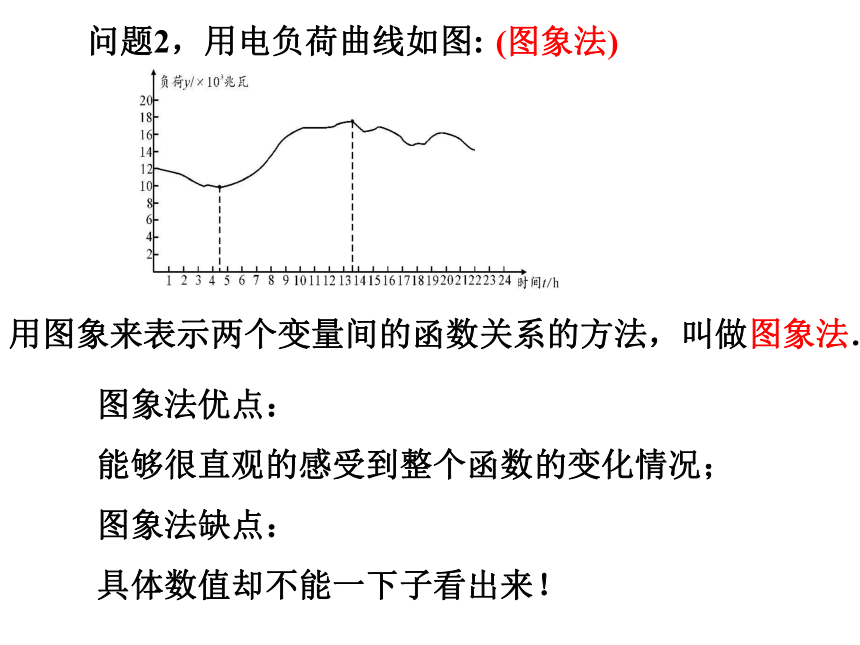
问题2,用电负荷曲线如图:
(图象法)
图象法优点:
能够很直观的感受到整个函数的变化情况;
图象法缺点:
具体数值却不能一下子看出来!
用图象来表示两个变量间的函数关系的方法,叫做图象法.
函数关系利用图象表示,直观、形象,
容易从中了解函数的一些变化情况。
如何画函数图象呢?
函数图象可以看作由点构成。
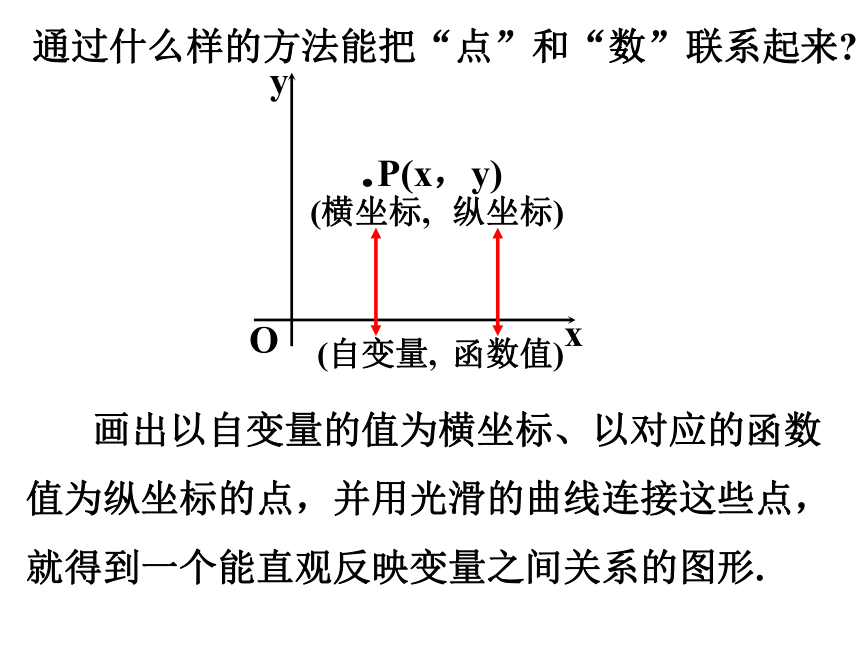
通过什么样的方法能把“点”和“数”联系起来
笛卡尔
(近代法国哲学家、物理学家、数学家)
我思故我在
笛卡尔
(近代法国哲学家、物理学家、数学家)
笛卡尔对数学最重要的贡献是创立了解析几何。
成功地将当时完全分开的代数和几何学联系到了一起.
y
x
O
P(x,y)
画出以自变量的值为横坐标、以对应的函数值为纵坐标的点,并用光滑的曲线连接这些点,就得到一个能直观反映变量之间关系的图形.
(自变量,
函数值)
(横坐标,
纵坐标)
通过什么样的方法能把“点”和“数”联系起来
函数关系利用图象表示,直观、形象,
容易从中了解函数的一些变化情况。
如何画函数图象呢?
下面通过画函数y=2x的图象来说明 .
x
y
o
-4
4
8
-6
6
4
2
-4
-2
-2
2
y=2x
画函数y=2x的图象 .
x
y
…
…
…
…
-6
-4
-2
0
2
4
6
解:(1)列表.
(2)描点.
(3)连线.
在 x 的取值范围内列出函数对应值表.
在平面直角坐标系中描点.
按照自变量由小到大的顺序,用光滑曲线顺次连接各点.
-3
-2
-1
0
1
2
3
x
y
o
-4
4
8
-6
6
4
2
-4
-2
-2
2
y=2x
画函数y=2x的图象 .
x
-3
-2
-1
0
1
2
3
y
…
…
…
…
-6
-4
-2
0
2
4
6
函数图象是坐标平面上以自变量的值为横坐标、以对应的函数值为纵坐标的点组成的曲线,函数图象直观地反映了变量之间的对应关系和变化规律.
例4 画出函数 的图象 .
S=
v2
256
解:(1)列表:
v
0
10
20
30
40
50
S
…
0
0.4
1.6
3.5
6.3
9.8
∵v≥0,
∴
v=0,
10,
20,
30,
40,
50,
求出它们对应的值,列成表格:
(2)描点:
在坐标平面内描出(0,0),(10,0.4),(20,1.6),(30,3.5),(40,6.3)等点.
例4 画出函数 的图象 .
S=
v2
256
解:(1)列表.
v
0
10
20
30
40
50
S
…
0
0.4
1.6
3.5
6.3
9.8
(2)描点.
(3)连线.
v
s
o
8
6
4
2
10
60
40
20
将以上各点按照自变量由小到大的顺序用平滑曲线连接
S=
v2
256
画函数图象的一般步骤:
1.列表.
2.描点.
3.连线.
在 x 的取值范围内列出函数对应值表.
在平面直角坐标系中描点.
按照自变量由小到大的顺序,用光滑曲线顺次连接各点.
这种画函数图象的方法称为描点法.
1.画出函数y=-2x的图象 .
x
-3
-2
-1
0
1
2
3
y
…
…
x
y
o
-4
4
8
-6
6
4
2
-4
-2
-2
2
6
4
2
0
-2
-4
-6
y=-2x
练习巩固
2.(1)画出函数y=-x的图象 .
(2)判断点A(- , ),B(0,0),C( ,- )
是否在函数y=-x的图象上.
3
2
3
2
3
2
3
2
练习巩固
x
-3
-2
-1
0
1
2
3
y
…
…
x
y
o
-4
4
8
-6
6
4
2
-4
-2
-2
2
3
2
1
0
-1
-2
-3
2.(1)画出函数y=-x的图象 .
y=-x
(2)判断点A(- , ),B(0,0),C( ,- )
是否在函数y=-x的图象上.
3
2
3
2
3
2
3
2
x
y
o
-4
4
8
-6
6
4
2
-4
-2
-2
2
y=-x
A
B
C
点A,B,C都在
函数y=-x的图象上.
3.如图,下列各曲线中哪些能够表示y是x的函数
你能说出其中的道理吗
曲线中(1)和(2)能够表示y是x的函数;
曲线中(3)和(4)不能表示y是x的函数;
∵对于自变量x,y不是有唯一的值和它对应.
1.下列各点中,在函数y= -x-1图象上的是( ).
A.(1 ,2) B. (1,0) C. (2 ,3) D. (2 ,-3)
巩固提高
2.函数y= 5x2的图象上不经过点( ).
A.(1 ,5) B. (-1,5) C. (0 ,0) D. (2 ,-10)
D
D
3.已知函数y= -3x+n的图象经过点(-2 ,5)
下列各点中,在这个函数图象上的是( ).
A. (0 , -2) B. (-3,8)
C. (-3 ,14) D. (-1 ,1)
B
∵函数y= -3x+n的图象经过点(-2 ,5)
∴5= -3×(-2)+n
∴n= -1
∴y= -3x -1
4.已知点A(-4 ,m)在函数y= -3x的图象上,则m的值为 .
5.已知点B(-1 ,3)在函数y= 2x+n的图象上,则n的值为 .
6.已知点C(-3 ,5)在函数y= ax2-4的图象上,则a的值为 .
12
5
1
7.用描点法画出函数y=2x+1(x≥0)的图象 .
x
0
1
2
3
4
y
…
…
x
y
o
-4
4
8
6
4
2
-2
-2
2
1
3
5
7
9
y=2x+1
今天作业
课本P31页第5、6题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
沪科版 八年级上册
12.1 函数 (3)
学习目标:
1.通过阅读教材了解函数图象法的意义.
2.经历画函数图象的过程,体会数形结合的特点,认识函数图象的意义,掌握函数图象的画法.
学习重难点:认识函数图象的意义,掌握函数
图象的画法.
1. 如何求函数自变量的取值范围?
函数y= 中,自变量x的取值范围是( )
A.x>1 B.x≥1 C.x>-2 D.x≥-2
A
x-1
x+2
在一个函数关系式中,同时有几种代数式,函数自变量的取值范围应是各种代数式中自变量取值范围的公共部分.
复习旧知
1. 如何求函数自变量的取值范围?
函数y= 中,自变量x的取值范围是( )
A.x>1 B.x≥1 C.x>-2 D.x≥-2
A
x-1
x+2
y=
x-1
x+2
x≥1
y=
x-1
x-2
x≥1,
但x≠2
2.函数的表示有几种形式?
问题1.用热气球探测高空气象:
时间 t/min 0 1 2 3 4 5 6 …
海拔高度h/m 1800 1830 1860 1890 1920 1950 1980 …
问题2,用电负荷曲线如图:
问题3,制动距离经验公式:
S= .
v2
256
(列表法)
(解析法)
(图象法)
学习新知
问题1.用热气球探测高空气象:
时间 t/min 0 1 2 3 4 5 6 …
海拔高度h/m 1800 1830 1860 1890 1920 1950 1980 …
(列表法)
列表法的优点:
每个自变量对应的因变量一目了然,一看就知道结果;
列表法的缺点:
变化规律不是很明显,不能或者不太好推出任意一个自变量时的因变量的值.
通过列出自变量的值与对应的函数值的表格来表示函数关系的方法叫做列表法.
问题3,制动距离经验公式:
S= .
v2
256
(解析法)
用关于自变量的数学式子表示函数与自变量之间的关系的方法,叫做解析法.
解析法优点:
自变量与因变量的关系一看就知道,
解析法缺点:
涉及到具体数量还要进行计算.
问题2,用电负荷曲线如图:
(图象法)
图象法优点:
能够很直观的感受到整个函数的变化情况;
图象法缺点:
具体数值却不能一下子看出来!
用图象来表示两个变量间的函数关系的方法,叫做图象法.
函数关系利用图象表示,直观、形象,
容易从中了解函数的一些变化情况。
如何画函数图象呢?
函数图象可以看作由点构成。
通过什么样的方法能把“点”和“数”联系起来
笛卡尔
(近代法国哲学家、物理学家、数学家)
我思故我在
笛卡尔
(近代法国哲学家、物理学家、数学家)
笛卡尔对数学最重要的贡献是创立了解析几何。
成功地将当时完全分开的代数和几何学联系到了一起.
y
x
O
P(x,y)
画出以自变量的值为横坐标、以对应的函数值为纵坐标的点,并用光滑的曲线连接这些点,就得到一个能直观反映变量之间关系的图形.
(自变量,
函数值)
(横坐标,
纵坐标)
通过什么样的方法能把“点”和“数”联系起来
函数关系利用图象表示,直观、形象,
容易从中了解函数的一些变化情况。
如何画函数图象呢?
下面通过画函数y=2x的图象来说明 .
x
y
o
-4
4
8
-6
6
4
2
-4
-2
-2
2
y=2x
画函数y=2x的图象 .
x
y
…
…
…
…
-6
-4
-2
0
2
4
6
解:(1)列表.
(2)描点.
(3)连线.
在 x 的取值范围内列出函数对应值表.
在平面直角坐标系中描点.
按照自变量由小到大的顺序,用光滑曲线顺次连接各点.
-3
-2
-1
0
1
2
3
x
y
o
-4
4
8
-6
6
4
2
-4
-2
-2
2
y=2x
画函数y=2x的图象 .
x
-3
-2
-1
0
1
2
3
y
…
…
…
…
-6
-4
-2
0
2
4
6
函数图象是坐标平面上以自变量的值为横坐标、以对应的函数值为纵坐标的点组成的曲线,函数图象直观地反映了变量之间的对应关系和变化规律.
例4 画出函数 的图象 .
S=
v2
256
解:(1)列表:
v
0
10
20
30
40
50
S
…
0
0.4
1.6
3.5
6.3
9.8
∵v≥0,
∴
v=0,
10,
20,
30,
40,
50,
求出它们对应的值,列成表格:
(2)描点:
在坐标平面内描出(0,0),(10,0.4),(20,1.6),(30,3.5),(40,6.3)等点.
例4 画出函数 的图象 .
S=
v2
256
解:(1)列表.
v
0
10
20
30
40
50
S
…
0
0.4
1.6
3.5
6.3
9.8
(2)描点.
(3)连线.
v
s
o
8
6
4
2
10
60
40
20
将以上各点按照自变量由小到大的顺序用平滑曲线连接
S=
v2
256
画函数图象的一般步骤:
1.列表.
2.描点.
3.连线.
在 x 的取值范围内列出函数对应值表.
在平面直角坐标系中描点.
按照自变量由小到大的顺序,用光滑曲线顺次连接各点.
这种画函数图象的方法称为描点法.
1.画出函数y=-2x的图象 .
x
-3
-2
-1
0
1
2
3
y
…
…
x
y
o
-4
4
8
-6
6
4
2
-4
-2
-2
2
6
4
2
0
-2
-4
-6
y=-2x
练习巩固
2.(1)画出函数y=-x的图象 .
(2)判断点A(- , ),B(0,0),C( ,- )
是否在函数y=-x的图象上.
3
2
3
2
3
2
3
2
练习巩固
x
-3
-2
-1
0
1
2
3
y
…
…
x
y
o
-4
4
8
-6
6
4
2
-4
-2
-2
2
3
2
1
0
-1
-2
-3
2.(1)画出函数y=-x的图象 .
y=-x
(2)判断点A(- , ),B(0,0),C( ,- )
是否在函数y=-x的图象上.
3
2
3
2
3
2
3
2
x
y
o
-4
4
8
-6
6
4
2
-4
-2
-2
2
y=-x
A
B
C
点A,B,C都在
函数y=-x的图象上.
3.如图,下列各曲线中哪些能够表示y是x的函数
你能说出其中的道理吗
曲线中(1)和(2)能够表示y是x的函数;
曲线中(3)和(4)不能表示y是x的函数;
∵对于自变量x,y不是有唯一的值和它对应.
1.下列各点中,在函数y= -x-1图象上的是( ).
A.(1 ,2) B. (1,0) C. (2 ,3) D. (2 ,-3)
巩固提高
2.函数y= 5x2的图象上不经过点( ).
A.(1 ,5) B. (-1,5) C. (0 ,0) D. (2 ,-10)
D
D
3.已知函数y= -3x+n的图象经过点(-2 ,5)
下列各点中,在这个函数图象上的是( ).
A. (0 , -2) B. (-3,8)
C. (-3 ,14) D. (-1 ,1)
B
∵函数y= -3x+n的图象经过点(-2 ,5)
∴5= -3×(-2)+n
∴n= -1
∴y= -3x -1
4.已知点A(-4 ,m)在函数y= -3x的图象上,则m的值为 .
5.已知点B(-1 ,3)在函数y= 2x+n的图象上,则n的值为 .
6.已知点C(-3 ,5)在函数y= ax2-4的图象上,则a的值为 .
12
5
1
7.用描点法画出函数y=2x+1(x≥0)的图象 .
x
0
1
2
3
4
y
…
…
x
y
o
-4
4
8
6
4
2
-2
-2
2
1
3
5
7
9
y=2x+1
今天作业
课本P31页第5、6题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
