专题1.1 探索勾股定理(第2课时)课件(共48张PPT)
文档属性
| 名称 | 专题1.1 探索勾股定理(第2课时)课件(共48张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-23 00:00:00 | ||
图片预览










文档简介
(共48张PPT)
八上数学同步精优课件
北师大版八年级上册
第一章 勾股定理
1.1 .1 探索勾股定理 (第2课时)
精优教学课件
新课导入
讲授新课
当堂检测
课堂小结
1、学会常用的几种方法验证勾股定理.(重点)
2、可以运用勾股定理解决简单问题.(重点,难点)
3、掌握常见的一些勾股数.(重点)
学习目标
勾股定理
几何语言:
∵在Rt △ABC, ∠C=90°(前提)
∴a2+b2=c2 (c为斜边)
a
b
c
直角三角形两直角边的平方和等于斜边的平方,
复习回顾
我们是怎样发现“勾股定理”的
割 -将正方形分割成4个全等直角三角形和1个小正方形
补-将正方形按图补成大正方形内部
复习回顾
你能用下列的图形验证勾股定理?
据不完全统计,验证的方法有400多种,你想得到自己的方法吗?
a2+b2=c2
复习回顾
导入新课
观察与思考
问题:将下面四个全等的直角三角形拼出以斜边为边长的正方形.
有不同的拼法吗?
讲授新课
考点一 勾股定理的验证
据不完全统计,验证的方法有400多种,你有自己的方法吗?
问题:上节课我们认识了勾股定理,你还记得它的内容吗?那么如何验证勾股定理呢 ?
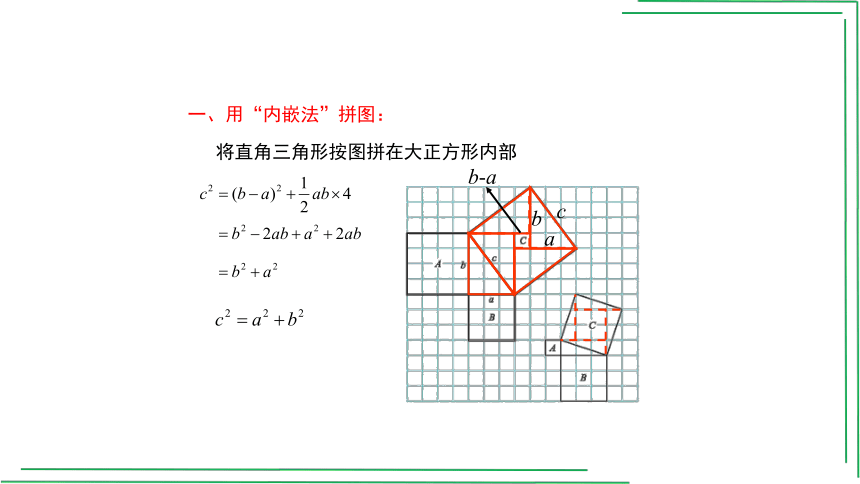
一、用“内嵌法”拼图:
将直角三角形按图拼在大正方形内部
b-a
a
b
c
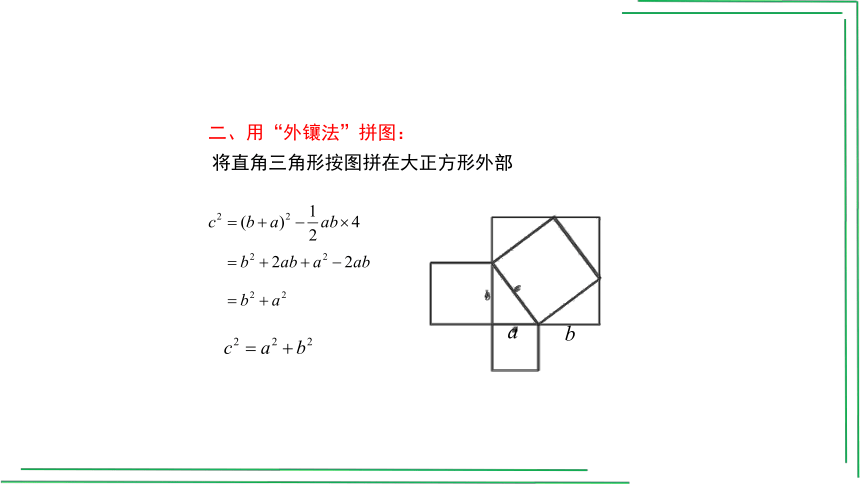
二、用“外镶法”拼图:
将直角三角形按图拼在大正方形外部
a
b
如图是美国总统伽菲尔德(Garfield)于1876年给出的一种验证勾股定理的办法,你能利用它验证勾股定理吗?说一说这个方法和本节的探索方法的联系。
三、“总统证明法”
如图,梯形由三个直角三角形组合而成,利用面积公式,列出代数关系式,得
化简,得
(2)拼梯形图:
运用梯形面积表达式进行证明。
新知归纳
“勾股定理”的验证方法:
(1)拼正方形图:
运用正方形面积表达式进行证明;
1、数形结合法:
考点二 勾股定理的简单应用
例:我方侦查员小王在距离东西向公路400m处侦查,发现一辆敌方汽车在公路上疾驶.他赶紧拿出红外测距仪,测得汽车与他相距400m,10s后,汽车与他相距500m,你能帮小王计算敌方汽车的速度吗
公路
B
C
A
400m
500m
解:由勾股定理,可以得到AB2=BC2+AC2,也就是5002=BC2+4002,所以BC=300.敌方汽车10s行驶了300m,那么它1h行驶的距离为300×6×60=108000(m),即它行驶的速度为108km/h.
练习
1. 在直角三角形中,满足条件的三边长可以是 .(写出一组即可)
【解析】答案不唯一,只要满足式子a2+b2=c2即可.
答案:3,4,5(满足题意的均可)
2 我方侦察员小王在距离东西向公路400米处侦察,发现一辆敌方汽车在公路上疾驶。他赶紧拿出红外测距仪,测得汽车与他相距400米,10秒后,汽车与他相距500米,你能帮助小王计算敌方汽车的速度吗?
解:在Rt△ABC中,根据勾股定理,
∴BC =AB -AC
=500 -400
=3002
∴BC=300 m
V敌方汽车=S÷t=300÷10=30 (m/s)
答:敌方汽车的速度为30 m/s
3.如图,一根旗杆在离地面9 m处折断,旗杆顶部落在离旗杆底部12 m处.旗杆原来有多高
12 m
9 m
解:设旗杆顶部到折断处的距离为x m,根据勾股定理得
解得x=15, 15+9=24(m).
答:旗杆原来高24 m.
A
2
1
-4
-3
-2
-1
-1
2
3
1
4
5
考点三 利用勾股定理求两点距离及验证“HL”
例 如图,在平面直角坐标系中有两点A(-3,5),B(1,2)求A,B两点间的距离.
y
O
x
3
B
C
解:如图,过点A作x轴的垂线,过点B作x,y轴的垂线.相交于点C,连接AB.
∴AC=5-2=3,BC=3+1=4,
在Rt△ABC中,由勾股定理得
∴A,B两点间的距离为5.
方法总结:两点之间的距离公式:一般地,设平面上任意两点
思考 在八年级上册中,我们曾经通过画图得到结论:斜边和一条直角边分别相等的两个直角三角形全等.学习了勾股定理后,你能证明这一结论吗?
已知:如图,在Rt△ABC 和Rt△A ′ B ′ C ′ 中,∠C=
∠C ′=90°,AB=A′ B ′,AC=A′ C′ .
求证:△ABC≌△A ′B ′C′ .
A
B
C
A
B
C′
′
′
证明:在Rt△ABC 和Rt△A ′B ′C ′中,
∠C=∠C′=90°,
根据勾股定理得
A
B
C
A
B
C′
′
′
C
B
A
问题 在A点的小狗,为了尽快吃到B点的香肠,它选择A B 路线,而不选择A C B路线,难道小狗也懂数学?
AC+CB >AB(两点之间线段最短)
思考 在立体图形中,怎么寻找最短线路呢?
考点四 利用勾股定理求最短距离
B
A
d
A
B
A'
A
B
B
A
O
想一想:蚂蚁走哪一条路线最近?
A'
蚂蚁A→B的路线
问题:在一个圆柱石凳上,若小明在吃东西时留下了一点食物在B处,恰好一只在A处的蚂蚁捕捉到这一信息,于是它想从A处爬向B处,蚂蚁怎么走最近?
B
A
根据两点之间线段最短易知第一个路线最近.
若已知圆柱体高为12 cm,底面半径为3 cm,π取3.
B
A
3
O
12
侧面展开图
12
3π
A
B
A'
A'
解:在Rt△ABA′中,由勾股定理得
立体图形中求两点间的最短距离,一般把立体图形展开成平面图形,连接两点,根据两点之间线段最短确定最短路线.
归纳
例5 有一个圆柱形油罐,要以A点环绕油罐建梯子,正好建在A点的正上方点B处,问梯子最短需多少米(已知油罐的底面半径是2 m,高AB是5 m,π取3)
A
B
A
B
A'
B'
解:油罐的展开图如图,则AB'为梯子的最短距离.
∵AA'=2×3×2=12, A'B'=5,
∴AB'=13. 即梯子最短需13米.
典例精析
数学思想:
立体图形
平面图形
转化
展开
B
牛奶盒
A
【变式题】看到小蚂蚁终于喝到饮料的兴奋劲儿,小明又灵光乍现,拿出了牛奶盒,把小蚂蚁放在了点A处,并在点B处放上了点儿火腿肠粒,你能帮小蚂蚁找到完成任务的最短路程么?
6cm
8cm
10cm
B
B1
8
A
B2
6
10
B3
AB12 =102 +(6+8)2 =296,
AB22= 82 +(10+6)2 =320,
AB32= 62 +(10+8)2 =360,
解:由题意知有三种展开方法,如图.由勾股定理得
∴AB1<AB2<AB3.
∴小蚂蚁完成任务的最短路程为AB1,长为 .
例5 如图,一个牧童在小河的南4km的A处牧马,而他正位于他的小屋B的西8km北7km处,他想把他的马牵到小河边去饮水,然后回家.他要完成这件事情所走的最短路程是多少?
牧童A
小屋B
A′
C
东
北
解:如图,作出点A关于河岸的对称点A′,连接A′B则A′B就是最短路线.
由题意得A′C=4+4+7=15(km),BC=8km.
在Rt△A′DB中,由勾股定理得
求直线同侧的两点到直线上一点所连线段的和的最短路径的方法:先找到其中一点关于这条直线的对称点,连接对称点与另一点的线段就是最短路径长,以连接对称点与另一个点的线段为斜边,构造出直角三角形,再运用勾股定理求最短路径.
归纳
如图,是一个边长为1的正方体硬纸盒,现在A处有一只蚂蚁,想沿着正方体的外表面到达B处吃食物,求蚂蚁爬行的最短距离是多少.
A
B
解:由题意得AC =2,BC=1,
在Rt△ABC中,由勾股定理得
AB = AC + BC =2 +1 =5,
∴AB= ,即最短路程为 .
2
1
A
B
C
练一练
补充练习:
1.湖的两端有A、B两点,从与BA方向成直角的BC方向上的点C测得CA=130米,CB=120米,则AB为( )
A
B
C
A.50米 B.120米 C.100米 D.130米
130
120
A
2.如图,王大爷准备建一个蔬菜大棚,棚宽8m,高6m,长20m,棚的斜面用塑料薄膜遮盖,不计墙的厚度,阳光透过的最大面积是_________.
200m2
3.如图,有两棵树,一棵高8米,另一棵2米,两棵对
相距8米.一只鸟从一棵树的树梢飞到另一棵的树梢,问小鸟至少飞行多少?
A
B
C
解:如图,过点A作AC⊥BC于点C.
由题意得AC=8米,BC=8-2=6(米),
答:小鸟至少飞行10米.
4 如图,受台风“圆规”影响,一棵高18米的大树断裂,树的顶部落在离树根底部6米处,这棵树折断后有多高?
6米
x
18-x
解:设这棵树折断后有x米高,则折断的部分为(18-x)米,根据勾股定理,得
∴x +6 =(18-x)
∴解得x=8 m
答:这棵树折断后有8米高
5.如图是某沿江地区交通图,为了加快经济发展,该地区拟修建一条连接M,O,Q三城市的沿江高速,已知沿江高速的建设成本是100万元/千米,该沿江高速的造价预计是多少?
解:在Rt△MNO中,
根据勾股定理,
∴OM =MN +NO
=300 +400
=5002
∴OM=500 km
同理,得 OQ=1300 km
∴沿江高速长为 OM+OQ=500 +1300=1800 km
∴该沿江高速的造价为 1800× 100=180000 万元
答:该沿江高速的造价预计是180000 万元
6.一个直角三角形的斜边为20cm,且两直角边的长度比为3︰4,求两直角边的长。
3x
4x
20
解:设这两直角边的长分别为3x cm和4x cm,根据勾股定理,得
∴(3x) +(4x) =20
∴解得x=4
∴3x=3×4=12 cm,
4x=4×4=16 cm
答:这两直角边的长分别
为12 cm和16cm
7.如图,马路边一根高为5.4m的电线杆,被一辆卡车从离地面1.5m处撞断裂,倒下的电线杆顶部是否会落在离它的底部A处4m的快车道上?
A
B
C
C`
解:在Rt△ABC中,
AB=1.5 m,BC=5.4-1.5=3.9 m
根据勾股定理,得
∴AC =BC -AB
=2.9 -1.5
=12.96<4
答:倒下的电线杆顶部会落在离它的底部A处4m的快车道上
8.如图,是一个三级台阶,它的每一级的长、宽和高分别等于55cm,10cm和6cm,A和B是这个台阶的两个相对的端点,A点上有一只蚂蚁,想到B点去吃可口的食物.这只蚂蚁从A点出发,沿着台阶面爬到B点,最短线路是多少?
B
A
A
B
C
解:台阶的展开图如图,连接AB.
在Rt△ABC中,根据勾股定理得
AB2=BC2+AC2=552+482=5329,
∴AB=73cm.
9.如图,在一条公路上有A、B两站相距25km,C、D为两个小镇,已知DA⊥AB,CB ⊥AB, DA=15km,CB= 10km,现在要在公路边上建设一个加油站E,使得它到两镇的距离相等,请问E站应建在距A站多远处
D
A
E
B
C
15
10
25-x
10.如图,折叠长方形ABCD的一边AD,使点D落在BC边的F点处,若AB=8cm,BC=10cm,求EC的长.
D
A
B
C
E
F
8
10
解:设EC为x cm,则DE为(8-x)cm
由折叠性质,得
AD=AF=10 cm
EF=DE=(8-x) cm
在Rt△ABC中,根据勾股定理,得
∴AC =BC -AB
=2.9 -1.5
=12.96<4
答:倒下的电线杆顶部会落在离它的底部A处4m的快车道上
D
A
B
C
E
F
8
10
解:设EC=x cm,则DE=(8-x)cm
由折叠性质,得
AD=AF=10 cm
EF=DE=(8-x) cm
在Rt△ABF中,根据勾股定理,得 ∴BF =AF -AB =10 -8 =6
∴BF=6 cm ∴FC=10-6=4 cm
在Rt△EFC中,根据勾股定理,得
∴ x +42=(8-x)2
解得x=3
则EC=3 cm
11.如图,一个25 m长的梯子AB,斜靠在一竖直的墙AO上,这时的AO距离为24 m,如果梯子的顶端A沿墙下滑4m,那么梯子底端B也外移4 m吗?
A
B
O
C
D
A
B
O
C
D
解:在Rt△AOB中,根据勾股定理,得 ∴OB =AB -AO =25 -24 =7
∴OB=7 cm
在Rt△COD中,CD=AB=25cm
OC=OB-AC=24-4=20cm,
由勾股定理,得
∴OD =CD -OC =25 -20 =15
∴OD =15cm
∴ BD=15-7=8 cm
∴那么梯子底端B也外移8 m
12.如图,某隧道的截面是一个半径为3.6米的半圆形,一辆高2.4米、宽3米的卡车能通过隧道吗?
O
A
C
B
解:
过点A作AB⊥OC于点B,
∵∠ABO=90°
∴AB2+OB2=OA2
且OA=3.6,OB=1.5
∴AB2+1.52=3.62
∴AB2=10.71
∵AB2> 32
∴卡车能通过隧道
课堂小结
知识:勾股定理
如果直角三角形两直角边长分别为a,b,斜边长为 c ,那么 .
方法:观察—猜想—探究—验证—归纳—应用;
思想:1. 特殊—一般
2. 数形结合思想
3. 方程的思想
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
八上数学同步精优课件
北师大版八年级上册
第一章 勾股定理
1.1 .1 探索勾股定理 (第2课时)
精优教学课件
新课导入
讲授新课
当堂检测
课堂小结
1、学会常用的几种方法验证勾股定理.(重点)
2、可以运用勾股定理解决简单问题.(重点,难点)
3、掌握常见的一些勾股数.(重点)
学习目标
勾股定理
几何语言:
∵在Rt △ABC, ∠C=90°(前提)
∴a2+b2=c2 (c为斜边)
a
b
c
直角三角形两直角边的平方和等于斜边的平方,
复习回顾
我们是怎样发现“勾股定理”的
割 -将正方形分割成4个全等直角三角形和1个小正方形
补-将正方形按图补成大正方形内部
复习回顾
你能用下列的图形验证勾股定理?
据不完全统计,验证的方法有400多种,你想得到自己的方法吗?
a2+b2=c2
复习回顾
导入新课
观察与思考
问题:将下面四个全等的直角三角形拼出以斜边为边长的正方形.
有不同的拼法吗?
讲授新课
考点一 勾股定理的验证
据不完全统计,验证的方法有400多种,你有自己的方法吗?
问题:上节课我们认识了勾股定理,你还记得它的内容吗?那么如何验证勾股定理呢 ?
一、用“内嵌法”拼图:
将直角三角形按图拼在大正方形内部
b-a
a
b
c
二、用“外镶法”拼图:
将直角三角形按图拼在大正方形外部
a
b
如图是美国总统伽菲尔德(Garfield)于1876年给出的一种验证勾股定理的办法,你能利用它验证勾股定理吗?说一说这个方法和本节的探索方法的联系。
三、“总统证明法”
如图,梯形由三个直角三角形组合而成,利用面积公式,列出代数关系式,得
化简,得
(2)拼梯形图:
运用梯形面积表达式进行证明。
新知归纳
“勾股定理”的验证方法:
(1)拼正方形图:
运用正方形面积表达式进行证明;
1、数形结合法:
考点二 勾股定理的简单应用
例:我方侦查员小王在距离东西向公路400m处侦查,发现一辆敌方汽车在公路上疾驶.他赶紧拿出红外测距仪,测得汽车与他相距400m,10s后,汽车与他相距500m,你能帮小王计算敌方汽车的速度吗
公路
B
C
A
400m
500m
解:由勾股定理,可以得到AB2=BC2+AC2,也就是5002=BC2+4002,所以BC=300.敌方汽车10s行驶了300m,那么它1h行驶的距离为300×6×60=108000(m),即它行驶的速度为108km/h.
练习
1. 在直角三角形中,满足条件的三边长可以是 .(写出一组即可)
【解析】答案不唯一,只要满足式子a2+b2=c2即可.
答案:3,4,5(满足题意的均可)
2 我方侦察员小王在距离东西向公路400米处侦察,发现一辆敌方汽车在公路上疾驶。他赶紧拿出红外测距仪,测得汽车与他相距400米,10秒后,汽车与他相距500米,你能帮助小王计算敌方汽车的速度吗?
解:在Rt△ABC中,根据勾股定理,
∴BC =AB -AC
=500 -400
=3002
∴BC=300 m
V敌方汽车=S÷t=300÷10=30 (m/s)
答:敌方汽车的速度为30 m/s
3.如图,一根旗杆在离地面9 m处折断,旗杆顶部落在离旗杆底部12 m处.旗杆原来有多高
12 m
9 m
解:设旗杆顶部到折断处的距离为x m,根据勾股定理得
解得x=15, 15+9=24(m).
答:旗杆原来高24 m.
A
2
1
-4
-3
-2
-1
-1
2
3
1
4
5
考点三 利用勾股定理求两点距离及验证“HL”
例 如图,在平面直角坐标系中有两点A(-3,5),B(1,2)求A,B两点间的距离.
y
O
x
3
B
C
解:如图,过点A作x轴的垂线,过点B作x,y轴的垂线.相交于点C,连接AB.
∴AC=5-2=3,BC=3+1=4,
在Rt△ABC中,由勾股定理得
∴A,B两点间的距离为5.
方法总结:两点之间的距离公式:一般地,设平面上任意两点
思考 在八年级上册中,我们曾经通过画图得到结论:斜边和一条直角边分别相等的两个直角三角形全等.学习了勾股定理后,你能证明这一结论吗?
已知:如图,在Rt△ABC 和Rt△A ′ B ′ C ′ 中,∠C=
∠C ′=90°,AB=A′ B ′,AC=A′ C′ .
求证:△ABC≌△A ′B ′C′ .
A
B
C
A
B
C′
′
′
证明:在Rt△ABC 和Rt△A ′B ′C ′中,
∠C=∠C′=90°,
根据勾股定理得
A
B
C
A
B
C′
′
′
C
B
A
问题 在A点的小狗,为了尽快吃到B点的香肠,它选择A B 路线,而不选择A C B路线,难道小狗也懂数学?
AC+CB >AB(两点之间线段最短)
思考 在立体图形中,怎么寻找最短线路呢?
考点四 利用勾股定理求最短距离
B
A
d
A
B
A'
A
B
B
A
O
想一想:蚂蚁走哪一条路线最近?
A'
蚂蚁A→B的路线
问题:在一个圆柱石凳上,若小明在吃东西时留下了一点食物在B处,恰好一只在A处的蚂蚁捕捉到这一信息,于是它想从A处爬向B处,蚂蚁怎么走最近?
B
A
根据两点之间线段最短易知第一个路线最近.
若已知圆柱体高为12 cm,底面半径为3 cm,π取3.
B
A
3
O
12
侧面展开图
12
3π
A
B
A'
A'
解:在Rt△ABA′中,由勾股定理得
立体图形中求两点间的最短距离,一般把立体图形展开成平面图形,连接两点,根据两点之间线段最短确定最短路线.
归纳
例5 有一个圆柱形油罐,要以A点环绕油罐建梯子,正好建在A点的正上方点B处,问梯子最短需多少米(已知油罐的底面半径是2 m,高AB是5 m,π取3)
A
B
A
B
A'
B'
解:油罐的展开图如图,则AB'为梯子的最短距离.
∵AA'=2×3×2=12, A'B'=5,
∴AB'=13. 即梯子最短需13米.
典例精析
数学思想:
立体图形
平面图形
转化
展开
B
牛奶盒
A
【变式题】看到小蚂蚁终于喝到饮料的兴奋劲儿,小明又灵光乍现,拿出了牛奶盒,把小蚂蚁放在了点A处,并在点B处放上了点儿火腿肠粒,你能帮小蚂蚁找到完成任务的最短路程么?
6cm
8cm
10cm
B
B1
8
A
B2
6
10
B3
AB12 =102 +(6+8)2 =296,
AB22= 82 +(10+6)2 =320,
AB32= 62 +(10+8)2 =360,
解:由题意知有三种展开方法,如图.由勾股定理得
∴AB1<AB2<AB3.
∴小蚂蚁完成任务的最短路程为AB1,长为 .
例5 如图,一个牧童在小河的南4km的A处牧马,而他正位于他的小屋B的西8km北7km处,他想把他的马牵到小河边去饮水,然后回家.他要完成这件事情所走的最短路程是多少?
牧童A
小屋B
A′
C
东
北
解:如图,作出点A关于河岸的对称点A′,连接A′B则A′B就是最短路线.
由题意得A′C=4+4+7=15(km),BC=8km.
在Rt△A′DB中,由勾股定理得
求直线同侧的两点到直线上一点所连线段的和的最短路径的方法:先找到其中一点关于这条直线的对称点,连接对称点与另一点的线段就是最短路径长,以连接对称点与另一个点的线段为斜边,构造出直角三角形,再运用勾股定理求最短路径.
归纳
如图,是一个边长为1的正方体硬纸盒,现在A处有一只蚂蚁,想沿着正方体的外表面到达B处吃食物,求蚂蚁爬行的最短距离是多少.
A
B
解:由题意得AC =2,BC=1,
在Rt△ABC中,由勾股定理得
AB = AC + BC =2 +1 =5,
∴AB= ,即最短路程为 .
2
1
A
B
C
练一练
补充练习:
1.湖的两端有A、B两点,从与BA方向成直角的BC方向上的点C测得CA=130米,CB=120米,则AB为( )
A
B
C
A.50米 B.120米 C.100米 D.130米
130
120
A
2.如图,王大爷准备建一个蔬菜大棚,棚宽8m,高6m,长20m,棚的斜面用塑料薄膜遮盖,不计墙的厚度,阳光透过的最大面积是_________.
200m2
3.如图,有两棵树,一棵高8米,另一棵2米,两棵对
相距8米.一只鸟从一棵树的树梢飞到另一棵的树梢,问小鸟至少飞行多少?
A
B
C
解:如图,过点A作AC⊥BC于点C.
由题意得AC=8米,BC=8-2=6(米),
答:小鸟至少飞行10米.
4 如图,受台风“圆规”影响,一棵高18米的大树断裂,树的顶部落在离树根底部6米处,这棵树折断后有多高?
6米
x
18-x
解:设这棵树折断后有x米高,则折断的部分为(18-x)米,根据勾股定理,得
∴x +6 =(18-x)
∴解得x=8 m
答:这棵树折断后有8米高
5.如图是某沿江地区交通图,为了加快经济发展,该地区拟修建一条连接M,O,Q三城市的沿江高速,已知沿江高速的建设成本是100万元/千米,该沿江高速的造价预计是多少?
解:在Rt△MNO中,
根据勾股定理,
∴OM =MN +NO
=300 +400
=5002
∴OM=500 km
同理,得 OQ=1300 km
∴沿江高速长为 OM+OQ=500 +1300=1800 km
∴该沿江高速的造价为 1800× 100=180000 万元
答:该沿江高速的造价预计是180000 万元
6.一个直角三角形的斜边为20cm,且两直角边的长度比为3︰4,求两直角边的长。
3x
4x
20
解:设这两直角边的长分别为3x cm和4x cm,根据勾股定理,得
∴(3x) +(4x) =20
∴解得x=4
∴3x=3×4=12 cm,
4x=4×4=16 cm
答:这两直角边的长分别
为12 cm和16cm
7.如图,马路边一根高为5.4m的电线杆,被一辆卡车从离地面1.5m处撞断裂,倒下的电线杆顶部是否会落在离它的底部A处4m的快车道上?
A
B
C
C`
解:在Rt△ABC中,
AB=1.5 m,BC=5.4-1.5=3.9 m
根据勾股定理,得
∴AC =BC -AB
=2.9 -1.5
=12.96<4
答:倒下的电线杆顶部会落在离它的底部A处4m的快车道上
8.如图,是一个三级台阶,它的每一级的长、宽和高分别等于55cm,10cm和6cm,A和B是这个台阶的两个相对的端点,A点上有一只蚂蚁,想到B点去吃可口的食物.这只蚂蚁从A点出发,沿着台阶面爬到B点,最短线路是多少?
B
A
A
B
C
解:台阶的展开图如图,连接AB.
在Rt△ABC中,根据勾股定理得
AB2=BC2+AC2=552+482=5329,
∴AB=73cm.
9.如图,在一条公路上有A、B两站相距25km,C、D为两个小镇,已知DA⊥AB,CB ⊥AB, DA=15km,CB= 10km,现在要在公路边上建设一个加油站E,使得它到两镇的距离相等,请问E站应建在距A站多远处
D
A
E
B
C
15
10
25-x
10.如图,折叠长方形ABCD的一边AD,使点D落在BC边的F点处,若AB=8cm,BC=10cm,求EC的长.
D
A
B
C
E
F
8
10
解:设EC为x cm,则DE为(8-x)cm
由折叠性质,得
AD=AF=10 cm
EF=DE=(8-x) cm
在Rt△ABC中,根据勾股定理,得
∴AC =BC -AB
=2.9 -1.5
=12.96<4
答:倒下的电线杆顶部会落在离它的底部A处4m的快车道上
D
A
B
C
E
F
8
10
解:设EC=x cm,则DE=(8-x)cm
由折叠性质,得
AD=AF=10 cm
EF=DE=(8-x) cm
在Rt△ABF中,根据勾股定理,得 ∴BF =AF -AB =10 -8 =6
∴BF=6 cm ∴FC=10-6=4 cm
在Rt△EFC中,根据勾股定理,得
∴ x +42=(8-x)2
解得x=3
则EC=3 cm
11.如图,一个25 m长的梯子AB,斜靠在一竖直的墙AO上,这时的AO距离为24 m,如果梯子的顶端A沿墙下滑4m,那么梯子底端B也外移4 m吗?
A
B
O
C
D
A
B
O
C
D
解:在Rt△AOB中,根据勾股定理,得 ∴OB =AB -AO =25 -24 =7
∴OB=7 cm
在Rt△COD中,CD=AB=25cm
OC=OB-AC=24-4=20cm,
由勾股定理,得
∴OD =CD -OC =25 -20 =15
∴OD =15cm
∴ BD=15-7=8 cm
∴那么梯子底端B也外移8 m
12.如图,某隧道的截面是一个半径为3.6米的半圆形,一辆高2.4米、宽3米的卡车能通过隧道吗?
O
A
C
B
解:
过点A作AB⊥OC于点B,
∵∠ABO=90°
∴AB2+OB2=OA2
且OA=3.6,OB=1.5
∴AB2+1.52=3.62
∴AB2=10.71
∵AB2> 32
∴卡车能通过隧道
课堂小结
知识:勾股定理
如果直角三角形两直角边长分别为a,b,斜边长为 c ,那么 .
方法:观察—猜想—探究—验证—归纳—应用;
思想:1. 特殊—一般
2. 数形结合思想
3. 方程的思想
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
